Похожие презентации:
Первообразная. Неопределенный интеграл и его свойства. Таблица основных интегралов
1. Первообразная. Неопределенный интеграл и его свойства. Таблица основных интегралов ЛЕКЦИЯ
Тема 6Первообразная. Неопределенный
интеграл и его свойства. Таблица
основных интегралов
ЛЕКЦИЯ
Калабухова
Галина Валентиновна
кандидат социологических наук, доцент
2. Вопросы темы
Понятие первообразной.Неопределенный интеграл и его свойства.
Таблица основных интегралов.
3. ПОНЯТИЕ ПЕРВООБРАЗНОЙ
4. Определение
Функция F(x) называется первообразной функциейдля функции f(x) на промежутке X, если в каждой
точке этого промежутка
F ( x ) f ( x )
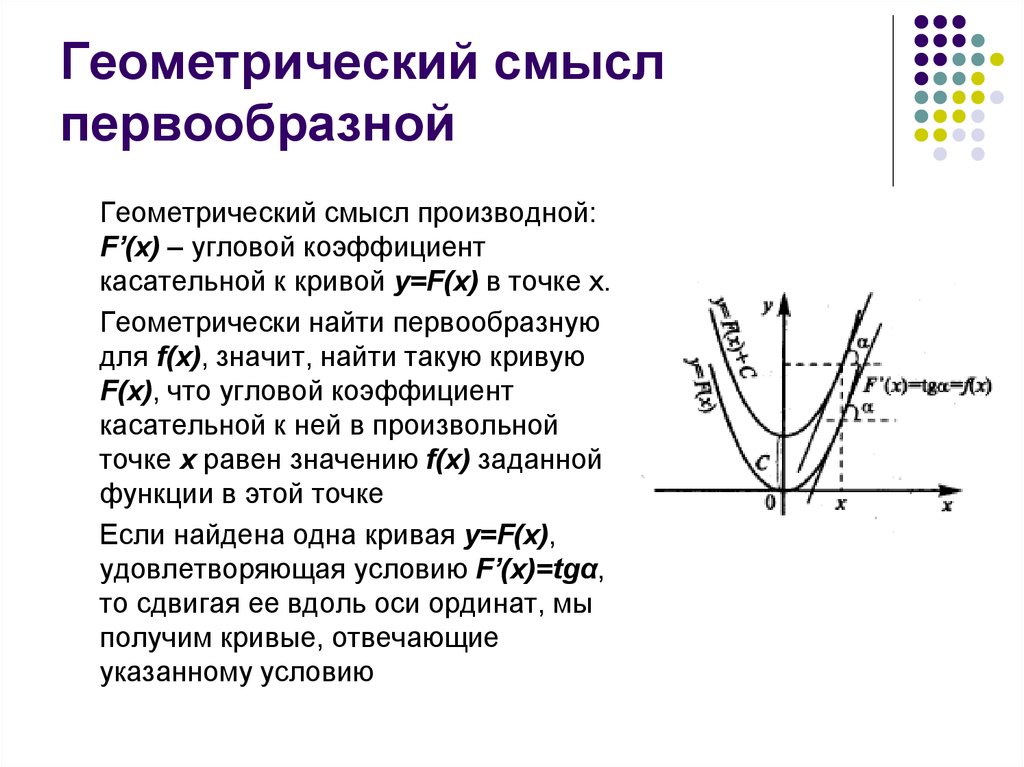
5. Геометрический смысл первообразной
Геометрический смысл производной:F’(x) – угловой коэффициент
касательной к кривой y=F(x) в точке x.
Геометрически найти первообразную
для f(x), значит, найти такую кривую
F(x), что угловой коэффициент
касательной к ней в произвольной
точке x равен значению f(x) заданной
функции в этой точке
Если найдена одна кривая y=F(x),
удовлетворяющая условию F’(x)=tgα,
то сдвигая ее вдоль оси ординат, мы
получим кривые, отвечающие
указанному условию
6. Теорема
Если F1(x) и F2(x) – первообразные для функции f(x)на промежутке X, то найдется такое число C, что
будет справедливо равенство
F2 ( x) F1 ( x) C
7. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА
8. Определение
Совокупность всех первообразных для функции f(x)на промежутке X, называется неопределенным
интегралом от функции f(x)
f ( x)dx F ( x) C
f(x) – подынтегральная функция
f(x)dx – подынтегральное выражение
F(x) – некоторая первообразная для f(x)
C – произвольная константа
9. Свойства неопределенного интеграла
Производная от неопределенного интеграла равнаподынтегральной функции:
f (x)dx
f ( x)
10. Свойства неопределенного интеграла
Дифференциал неопределенного интеграла равенподынтегральному выражению:
d f ( x) dx f ( x) dx
11. Свойства неопределенного интеграла
Неопределенный интеграл от дифференциаланекоторой функции равен этой функции с точностью
до постоянного слагаемого:
dF ( x) F ( x) C
12. Свойства неопределенного интеграла
Постоянный множитель можно выносить за знакинтеграла:
f ( x)dx f ( x)dx
13. Свойства неопределенного интеграла
Интеграл от алгебраической суммы двух функцийравен такой же сумме интегралов от этих функций:
( f ( x) g ( x))dx f ( x)dx g ( x)dx
14. ТАБЛИЦА ОСНОВНЫХ ИНТЕГРАЛОВ
15.
x n 1x dx n 1 c n 1
dx
x ln x c
n
dx
x
x
arcsin c arccos c
a
a
a2 x2
ax
a dx ln a c
x
e dx e
x
x
c
dx
x
ln
tg
c
sin x
2
dx
x
ln
tg
c
cos x
2 4
dx
1
x
arctg
c
x2 a2 a
a
sin xdx cos x c
shxdx chx c
dx
1
x a
ln
x 2 a 2 2a x a c
cos xdx sin x c
chx shx c
dx
1
a x
ln
a 2 x 2 2a a x c
dx
cos 2 x tgx c
dx
ch 2 x thx c
dx
sin 2 x ctgx c
dx
sh 2 x cthx c
dx
x2 a
ln | x x 2 a | c
16. НЕКОТОРЫЕ ПОЛЕЗНЫЕ ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ ИНТЕГРАЛОВ
17.
Еслиf (x)dx F (x) C
f (x b)dx F (x b) C
1
f ( ax) dx F ( ax) C
a
1
f (b ax) dx F ( ax b) C
a
, то:
18. СПЕЦИАЛЬНЫЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ ИНТЕГРАЛОВ
19. Интегрирование методом замены переменной (метод подстановки)
Пусть f ( x )dx F ( x ) Cтогда:
,
f (t( x))t ( x)dx F (t( x)) C
где t(x) - дифференцируемая монотонная функция
20. Методы замены переменной
1.Если в подынтегральной функции удаётся сразу
заметить оба сомножителя, и f(t(x)), и t’(x), то
замена переменной осуществляется подведением
множителя t’(x) под знак дифференциала:
t’(x)dx = dt, и задача сводится к вычислению
интеграла f (t )dt
21. Методы замены переменной
2.Замену переменной можно осуществлять
формальным сведением подынтегрального
выражения к новой переменной
22. Интегрирование по частям
Пусть u(x) и v(x) - функции, имеющие непрерывныечастные производные.
Тогда по формуле дифференцирования
произведения
d(uv) = u∙dv + v∙du → u∙dv = d(uv) - v∙du.
Находим неопределённые интегралы для обеих
частей этого равенства (при этом d (uv ) uv C ):
u dv uv v du
Или:
u v dx uv v u dx
23. Сведение интеграла «к самому себе»
С помощью интегрирования по частям (возможно,неоднократного) интеграл выражается через такой
же интеграл; в результате получается уравнение
относительно этого интеграла, решая которое,
находим значение интеграла
24. Рекуррентные соотношения
Если подынтегральная функция зависит отнекоторого параметра n, и получено соотношение,
которое выражает интеграл через аналогичный
интеграл с меньшим значением n, то это
соотношение и называется рекуррентным
соотношением
25. «Неберущиеся» интегралы
Производная элементарной функциитакже является элементарной функцией.
При нахождении первообразной
существуют функции, первообразные для
которых элементарными функциями не
являются.
Соответствующие интегралы
называются неберущимися в
элементарных функциях, в сами
функции – неинтегрируемыми в
конечном виде
e dx
sin x dx
cos x dx
x2
2
2
sin x
x dx
cos x
x dx
dx
ln x






















 Математика
Математика








