Похожие презентации:
Правильные многогранники
1.
ГБПОУ ВО Владимирский строительный колледжПравильные
многогранники
Преподаватель математики
Шаипкина Светлана
Алексеевна
2. Цель: создание условий для изучения понятия, элементов и свойств правильных многогранников
3.
•Что такое многоугольник?•Приведите примеры многоугольников
•Какой многоугольник называется
правильным?
•Приведите примеры правильных
многоугольников
•Что такое многогранник?
•Приведите примеры многогранников
•Перечислите основные элементы
многогранников
4.
№1№2
№4
№5
№3
5.
Заполните таблицуЧисло
Многогранник Граней Вершин
№1
№2
№3
№4
№5
Ребер
Количество
ребер,
сходящихся
в каждой
вершине
6.
Выпуклый многогранникназывается правильным, если его
грани являются правильными
многоугольниками и в каждой
вершине многогранника сходится
одно и то же число ребер
7.
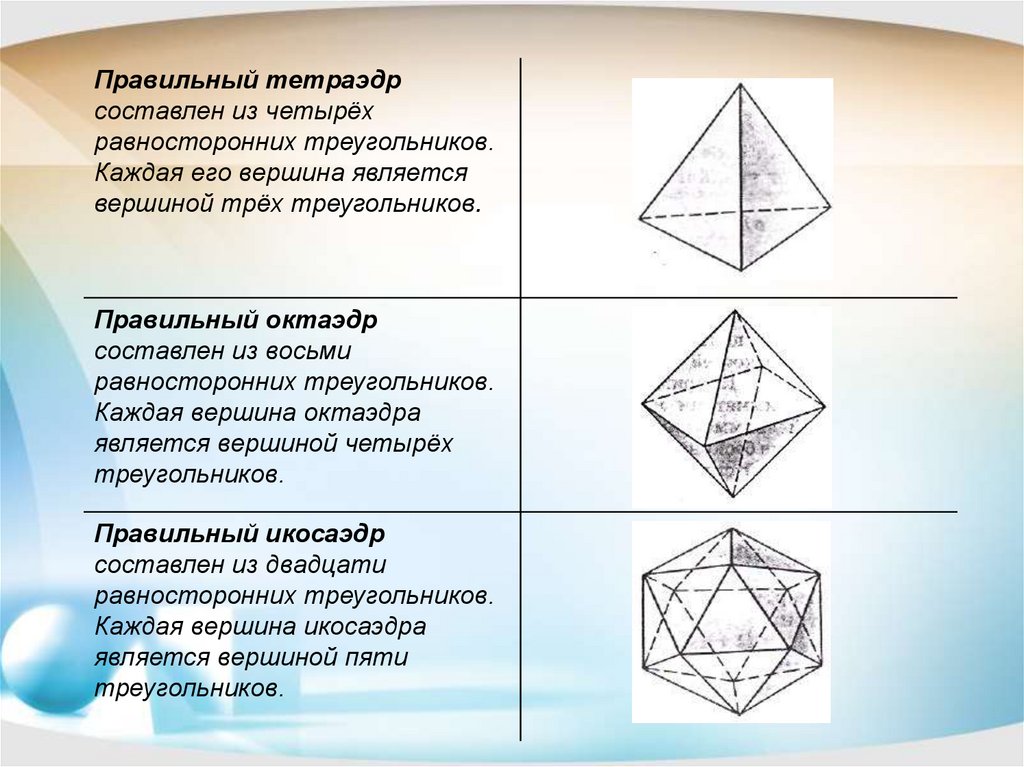
Правильный тетраэдрсоставлен из четырёх
равносторонних треугольников.
Каждая его вершина является
вершиной трёх треугольников.
Правильный октаэдр
составлен из восьми
равносторонних треугольников.
Каждая вершина октаэдра
является вершиной четырёх
треугольников.
Правильный икосаэдр
составлен из двадцати
равносторонних треугольников.
Каждая вершина икосаэдра
является вершиной пяти
треугольников.
8.
Куб (гексаэдр) составлен изшести квадратов. Каждая
вершина куба является
вершиной трёх квадратов.
Правильный додекаэдр
составлен из двенадцати
правильных пятиугольников.
Каждая вершина додекаэдра
является вершиной трёх
правильных пятиугольников.
Названия этих многогранников пришли из Древней Греции,
и в них указывается число граней: «эдра» - грань
«тетра» - 4
«окта» - 8
«гекса» - 6
«икоса» - 20
«додека» - 12
9.
Правильные многогранники иногда называютплатоновыми телами, поскольку они занимают видное
место в философской картине мира, разработанной
великим мыслителем Древней Греции Платоном (ок. 428 –
ок. 348 до н.э.).
10.
Платон считал, что мир строится из четырёх«стихий» - огня, земли, воздуха и воды, а атомы этих
«стихий» имеют форму четырёх правильных
многогранников. Пятый многогранник – додекаэдр
символизировал весь мир и почитался главнейшим.
огонь
тетраэдр
11.
водаикосаэдр
воздух
октаэдр
12.
землявселенная
гексаэдр
додекаэдр
13.
Правильные многогранники встречаются в живойприроде. Например, скелет одноклеточного организма
феодарии (Circjgjnia icosahtdra) по форме напоминает
икосаэдр.
14.
Чем же вызвана такая природная геометризацияфеодарий? По-видимому, тем, что из всех
многогранников с тем же числом граней именно
икосаэдр имеет наибольший объём при наименьшей
площади поверхности. Это свойство помогает морскому
организму преодолевать давление водной толщи.
15.
Природа широко пользуется правильнымимногогранниками. Подтверждением тому служит форма
некоторых кристаллов. Взять хотя бы поваренную соль, без
которой мы не можем обойтись. Известно, что она
растворима в воде, служит проводником электрического
тока. А кристаллы поваренной соли (NaCl) имеют форму
куба.
16.
При производстве алюминияпользуются алюминиевокалиевыми кварцами
(K[Al(SO4)2] × 12H2O),
монокристалл которых имеет
форму правильного октаэдра.
Получение серной кислоты,
железа, особых сортов
цемента не обходится без
сернистого колчедана (FeS).
Кристаллы этого
химического вещества
имеют форму додекаэдра .
17.
В разных химических реакцияхприменяется сурьменистый
сернокислый натрий
(Na5(SbO4(SO4)) – вещество,
синтезированное учёными.
Кристалл сурьменистого
сернокислого натрия имеет
форму тетраэдра.
Последний правильный
многогранник – икосаэдр
передаёт форму кристаллов бора
(В). В своё время бор
использовался для создания
полупроводников первого
поколения.
18.
Заполните таблицуЧисло
Правильный
многогранник
Граней
Тетраэдр
Куб
Октаэдр
Додекаэдр
Икосаэдр
Вершин
Ребер
19.
Заполните таблицуЧисло
Правильный
многогранник
Тетраэдр
Куб
Октаэдр
Додекаэдр
Икосаэдр
граней и вершин
(Г + В)
рёбер
(Р)
20.
Формула, которая была подмечена Декартом в 1640 г., апозднее вновь открыта Эйлером (1752), имя которого с тех
пор она носит.
Сумма числа граней и вершин равна
числу рёбер, увеличенному на 2, т.е.
Г+В=Р+2
Формула Эйлера верна для любых выпуклых
многогранников.
21.
Большой интерес к формам правильных многогранниковпроявляли также скульпторы, архитекторы, художники.
Их всех поражало совершенство, гармония многогранников.
Леонардо да Винчи (1452 – 1519) увлекался теорией
многогранников и часто изображал их на своих полотнах.
Сальвадоре Дали на картине «Тайная вечеря» изобразил И.
Христа со своими учениками на фоне огромного
прозрачного додекаэдра
22.
23.
−Почему правильные многогранники назвали«Платоновы тела»?
−Проанализируйте высказывание Л. Кэролла:
«Правильных многогранников вызывающе мало, но
этот весьма скромный по численности отряд сумел
пробраться в самые глубины различных наук»
24.
ТестВариант 1
1. Сколько правильных
многогранников существует в
геометрии?
1)3
2)7
3)5
4)6
Вариант 2
1.Какие из предложенных
многогранников правильные?
1)пирамида, куб
2)куб, октаэдр
3)призма, октаэдр
4)тетраэдр, параллелепипед
2. Какой из математиков
установил соотношения между
числом вершин, ребер и граней
выпуклого многогранника?
1)Платон
2)Архимед
3)Эйлер
4)Кеплер
2. Какой из математиков впервые
ввел понятия правильных
многогранников?
1)Платон
2)Архимед
3)Эйлер
4)Кеплер
25.
3. Сколько ребер может сходитьсяв одной вершине правильного
многогранника?
1)3, 4 или 5;
2)3 или 4;
3)3 или 5;
4)4 или 5;
4. Укажите фигуру:
1)Додекаэдр
2)Икосаэдр
3)Тетраэдр
4)гексаэдр
5. У каких правильных
многогранников гранями
являются правильные
треугольники?
1)Тетраэдр, гексаэдр, октаэдр
2)Тетраэдр, октаэдр, додекаэдр
3)Октаэдр, гексаэдр, икосаэдр
4)Икосаэдр, октаэдр, додекаэдр
3. Какой правильный n-угольник
не может быть гранью
правильного многогранника?
1)n = 4;
2)n = 3;
3)n = 5;
4)n = 6.
4. Укажите фигуру:
1)Додекаэдр
2)Икосаэдр
3)Тетраэдр
4)гексаэдр
5. Укажите верное утверждение:
1)правильный додекаэдр состоит
из восьми правильных
треугольников;
2)правильный тетраэдр состоит
из восьми правильных
треугольников;
3)правильный октаэдр состоит из
восьми правильных
треугольников
26.
Рефлексиясегодня у меня не получилось…
самым сложным для меня оказалось…
сегодня я научился…
больше всего мне
понравилось…
самым интересным для меня было...
27.
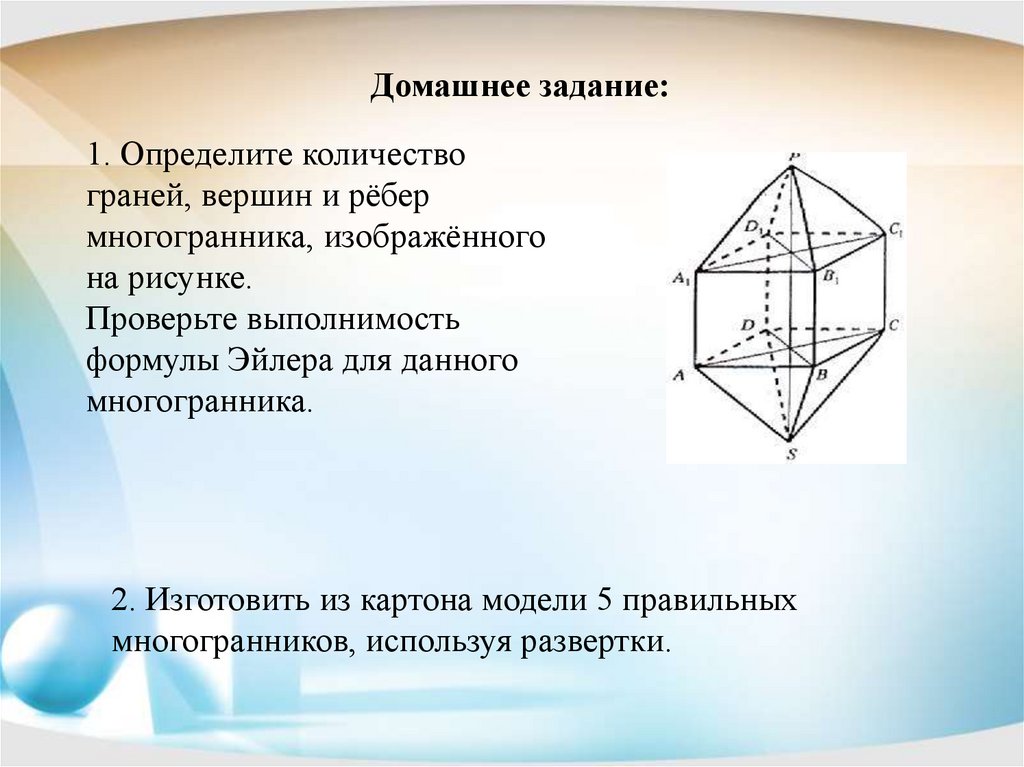
Домашнее задание:1. Определите количество
граней, вершин и рёбер
многогранника, изображённого
на рисунке.
Проверьте выполнимость
формулы Эйлера для данного
многогранника.
2. Изготовить из картона модели 5 правильных
многогранников, используя развертки.


























 Математика
Математика