Похожие презентации:
Задачи математической статистики
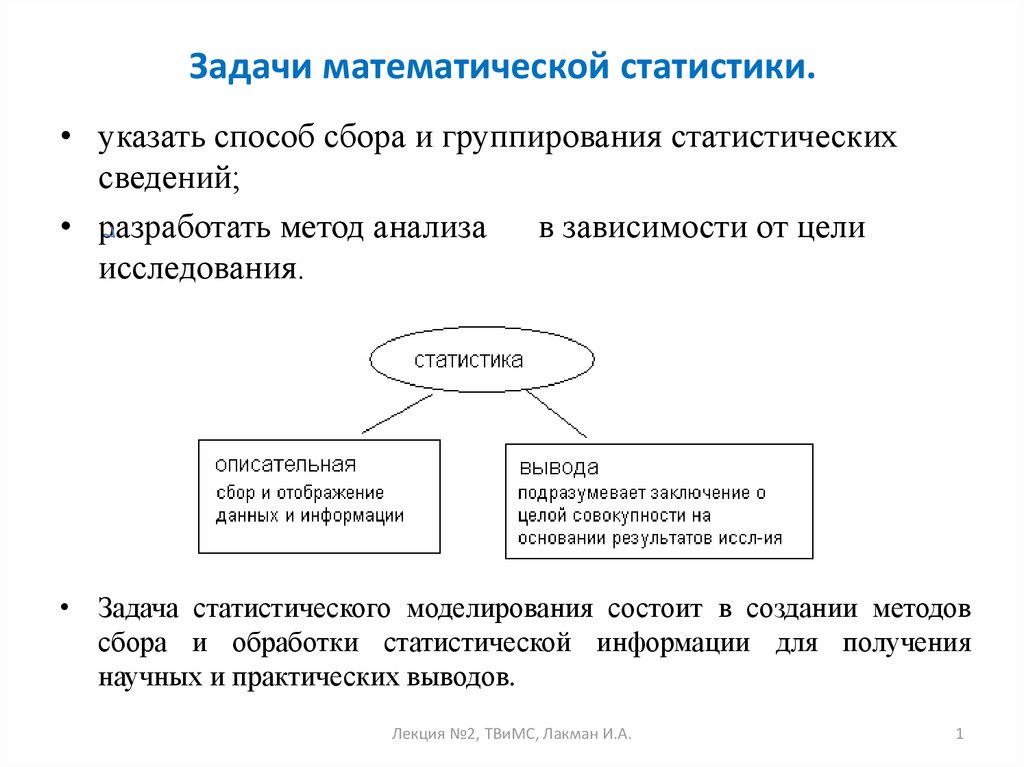
1. Задачи математической статистики.
• указать способ сбора и группирования статистическихсведений;
• разработать метод анализа в зависимости от цели
исследования.
• Задача статистического моделирования состоит в создании методов
сбора и обработки статистической информации для получения
научных и практических выводов.
Лекция №2, ТВиМС, Лакман И.А.
1
2. Статистическое распределение выборки
Определение: Выборочной совокупностью (выборкой) называетсясовокупность случайно отобранных объектов из генеральной
совокупности. К выборке предъявляется условие представительности или
репрезентативности, т.е. выборка должна правильно представлять
генеральную совокупность, для этого необходимо, чтобы объекты
выборки были отобраны случайно.
Определение: Генеральной совокупностью называется
совокупность, из которой производиться выборка.
Пусть из генеральной совокупности извлечена выборка, причем
значение Х1 наблюдалось n1 раз, Х2 -- n2 раз, …, Хk -- nk раз.
k
Тогда:
ni
i 1
n где n - общее число наблюдений (объем выборки).
,
Лекция №2, ТВиМС, Лакман И.А.
2
3. Статистическое распределение выборки
Определение: Наблюдаемые значения Хi называют вариантами, апоследовательность вариант, записанных в возрастающем порядке –
вариационным рядом. Число наблюдений ni называют частотами, а их
отношение к объему выборки называют относительными частотами
ni
.
n
Wi
Определение: Статистическим распределением выборки называют
перечень вариант и соответствующих им относительных частот.
Пусть известно статическое распределение частот количественного
признака Х. Пусть nх - число наблюдений, при которых наблюдалось
значение признака X меньшее х; n – общее число наблюдений, тогда
относительная частота события Х<х равна n x .
n
Лекция №1, ТВиМС, Лакман И.А.
3
4. Статистическое распределение выборки
Определение: Эмпирической функцией распределения (функциейраспределения выборки) называется функция F*(x), определяющая для
каждого значения х относительную частоту появления события Х<х.
Для наглядности статистического распределения в случае дискретного
распределения признака Х строят полигон (ломанная, где длина Х
откладывается на оси абсцисс, а на оси ординат соответствующие им
частоты ni).
В случае непрерывного распределения признака Х строят гистограммы.
Для построения гистограммы
все наблюдаемые значения признака
разбивают на несколько i частичных интервалов длиной h, и для каждого
интервала сумму частот вариант попавших в i интервал отмечают по оси
ординат. Гистограммой распределения частот называют ступенчатую
фигуру, состоящую из прямоугольников, основаниями которых служат
частичные интервалы длиной h, а высоты равны отношению ni (плотность
n
частот).
Лекция №1, ТВиМС, Лакман И.А.
4
5. Построение гистограмм
Задача 1. Даны данные о количестве ежедневных звонков абонента ссотового телефона: 5, 6, 10, 12, 4, 6, 0, 3, 15, 20, 14, 13, 11, 8, 10, 7, 6, 10,
12, 16, 18, 10, 14, 12, 5, 7, 16, 8, 9, 12. Построить гистограммы частот и
относительных частот распределения телефонных звонков в месяц.
Решение: Объем выборки п=30. Выберем длину частичного интервала h в
4 звонка. Тогда получим следующее распределение выборки.
Номер
Частичный
интервала, i интервал
xi – xi+1
1
2
3
4
5
0–4
5–8
9 – 12
13 – 16
17 – 20
Сумма
частот
вариант
интервала,
ni
3
9
10
6
2
Плотность
частоты,
ni/h
0,75
2,25
2,5
1,5
0,5
∑ ni =30
Лекция №1, ТВиМС, Лакман И.А.
Относительные частоты, wi=ni/n
0,1
0,3
0,33
0,2
0,07
∑ wi =1
5
6. Построение гистограмм
Строим гистограмму распределения частот, откладывая по осиабсцисс заданные интервалы длиной h=4, а параллельно оси ординат
высоты длиной ni/h.
Для построения гистограммы распределения
относительных частот – откладываем параллельно оси ординат высоты
длиной wi=ni/n .
Гистограмма распределения
частот звонков.
Гистограмма распределения
относительных частот звонков.
Лекция №2, ТВиМС, Лакман И.А.
6
7. Свойства оценок
Пусть имеются данные выборки, например значения некоторогопризнака, Х1, Х2,…, Хn, полученные в результате n наблюдений. Для того
чтобы найти статистическую оценку θ неизвестного параметра
теоретического распределения через эти данные необходимо найти
функцию от наблюдаемых случайных величин, которые дают
приближенное значение оцениваемого параметра. Статистическую оценку,
которая определяется одним числом, называют точечной.
Полученные оценки должны быть достоверными, т.е. обладать свойствами
несмещенности, эффективности и состоятельности.
• Несмешанной называют статистическую оценку θ*, математическое
ожидание которой равно оценивающему параметру θ при любом объеме
выборки, т.е. М(θ*)= θ .
• Эффективной оценкой называют статистическую оценку θ*, которая
при заданном объеме выборки n имеет наименьшую возможную
дисперсию.
• Состоятельной называют статистическую оценку, которая при n→ ∞ и
стремится по вероятности к оцениваемому параметру, т.е. . lim P ( *)
Лекция №1, ТВиМС, Лакман И.А.
n
7
8. Средняя величина
Определение: Генеральной средней Х г называется среднееарифметическое значение признаков генеральной совокупности:
( х х2 ..... х N )
,
(1)
Xг 1
N
где N – объем генеральной совокупности.
Если х1 встречается N1 раз, х2 – N2 раз и т.д., то (1) можно
переписать в виде:
Xг
( х1 N 1 х2 N 2 ..... хn N n )
N
(1)
Определение: Несмещенной оценкой генеральной средней служит
выборочная средняя, определяемая как среднее арифметическое
значение признаков выборки (ni частоты появления признака):
( х1 х 2 ..... х k ) или
( х1n1 х2 n2 ..... хk nk ) (2).
XB
n
XB
n
Средняя величина позволяет сделать вывод о центральном или
наиболее общем значении, найденном для совокупности данных.
Лекция №1, ТВиМС, Лакман И.А.
8
9. Дисперсия
Определение:Генеральной
дисперсией
называют
среднее
арифметическое квадратов отклонений
признака генеральной
совокупности от ее среднего
значения.
n
( xi X г ) 2
D 2 г i 1
(3)
n
Определение: Смещенной оценкой генеральной дисперсии служит
выборочная дисперсия, определяемая как:
n
DB
( xi X B ) 2
i 1
. (4)
Определение: Несмещенной оценкой генеральной дисперсии служит
исправленная выборочная дисперсия, определяемая:
n
n
S2
n
DB
n 1
( xi X B ) 2
i 1
n 1
(5)
• Мера рассеяния (дисперсия) показывает, насколько данные
распределены относительно среднего значения признака.
Лекция №1, ТВиМС, Лакман И.А.
9
10. Описательные статистики вариации
Генеральноесреднеквадратичное
отклонение
соответственно по формулам:
,
.
B DB
г Dг
определяется
Определение: Несмещенной оценкой среднего квадратического
отклонения является стандартное отклонение, определяемое по формуле:
n
s
( xi X ) 2
i 1
(6)
n 1
Определение: Модой называется это наиболее часто наблюдаемая величина
случайной переменной, обозначается М0. Для дискретного ряда мода равна
максимальной частоте, для интервального вариационного ряда определяется
модальный интервал по наибольшей частоте, а мода определяется как:
(nMo nMo 1)
M o x0 i
(nMo nMo 1) (nMo nMo 1)
Здесь nMo , nMo 1, nMo 1
- частоты модального, предмодального и
постмодального интервалов; а Х0 и i – нижняя граница и величина модельного
интервала.
Лекция №1, ТВиМС, Лакман И.А.
10
11. Показатели центра распределения
Определение: Медианой называется значение наблюдения, котороенаходиться в середине ранжированного ряда данных, т.е. наблюдение,
занимающее серединное значение, обозначается как Ме.
Для интервального вариационного ряда определяется: модальный интервал по
наибольшей частоте, а мода определяется как:
k
1 / 2 ni S Me 1
M e x0 i
i 1
nMe
Здесь nMe - частота медианного интервала; S Me 1 - кумулятивная частота
предмедианного интервала; а Х0 и i – нижняя граница и величина медианного
интервала.
Лекция №1, Анализ данных, Лакман И.А.
11
12. Порядковые характеристики
Определение: Квартили Q - это значения вариантов признака, которые делятвариационный ряд по объему на четыре равные части.
k
Первый квартиль: Q x i
1
Q1
0,25 ni SQ1 1
i 1
nQ1
k
Третий квартиль:
Q3 xQ3 i
0,75 ni SQ3 1
i 1
nQ3
Второй квартиль равен медиане.
Определение: Децили D - это значения вариантов признака, которые делят
вариационный ряд по объему на десять равных частей, а процентили P
соответственно на 100.
Первая дециль:
Первая процентиль
k
k
D1 xD1 i
0,1 ni S D1 1
i 1
nD1
P1 xP1 i
Лекция №1, Анализ данных, Лакман И.А.
0,1 ni S P1 1
i 1
nP1
12
13. Показатели вариации
Определение: Среднеквадратичное отклонение определяетсясоответственно для сгруппированных и несгруппированных данных по
формуле:
,2
.
D
Среднеквадратичное отклонение дает неискаженное представление о б
отклонении, в отличие от дисперсии.
Для колеблиемости данных вводят также:
Коэффициент осцилляции: V R 100 %
R
x
Коэффициент вариации: V 100%
x
Q3 Q1
V
Квартильный коэффициент вариации: Q
2Me
D9
V
Децильный коэффициент вариации:
D
D1
Лекция №1, Анализ данных, Лакман И.А
13
14. Асимметрия
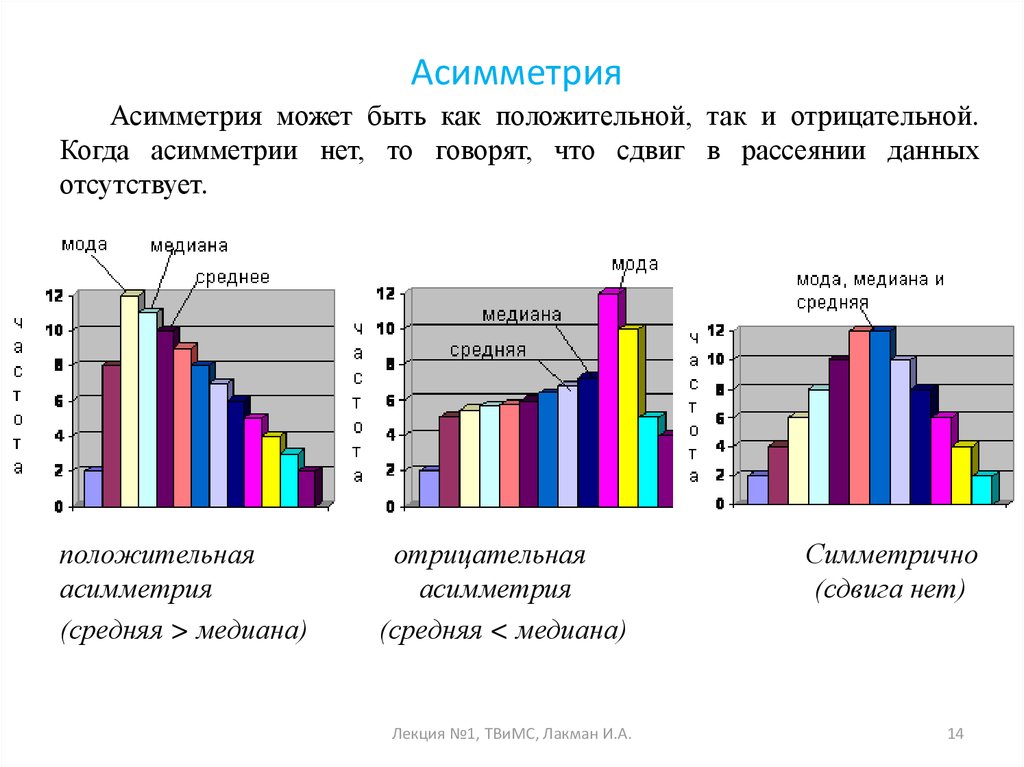
Асимметрия может быть как положительной, так и отрицательной.Когда асимметрии нет, то говорят, что сдвиг в рассеянии данных
отсутствует.
положительная
асимметрия
(средняя > медиана)
отрицательная
асимметрия
(средняя < медиана)
Лекция №1, ТВиМС, Лакман И.А.
Симметрично
(сдвига нет)
14
15. Коэффициент асимметрии
Определение: Коэффициент асимметриисмещение (скошенность) в рассеянии данных.
Коэффициент асимметрии определяется:
показывает,
есть
ли
( х Х )3
КА
n 1
2
x X
n 1
3
(7)
Коэффициент асимметрии Спирмена определяется как:
КАспир
3(средняя_ арифметическая медиана )
среднее _ квадратическое _ оклонение (8)
Коэффицент асимметрии является моментом третьего порядка
Лекция №1, ТВиМС, Лакман И.А.
15
16. Эксцесс
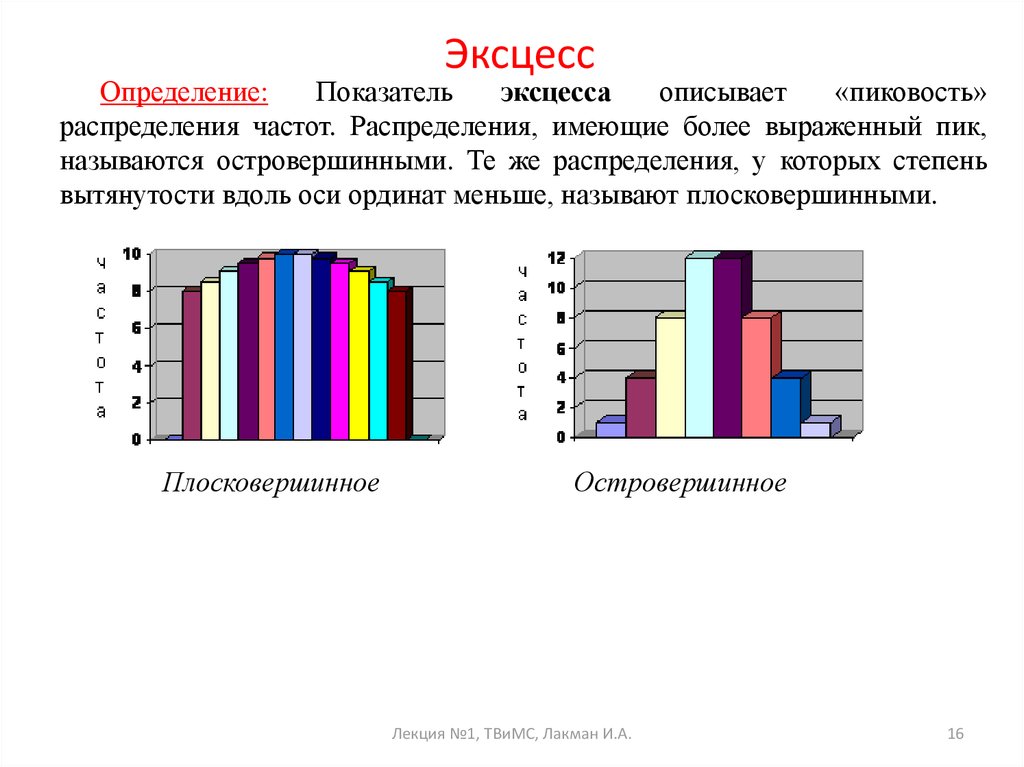
Определение:Показатель
эксцесса
описывает
«пиковость»
распределения частот. Распределения, имеющие более выраженный пик,
называются островершинными. Те же распределения, у которых степень
вытянутости вдоль оси ординат меньше, называют плосковершинными.
Плосковершинное
Островершинное
Лекция №1, ТВиМС, Лакман И.А.
16
17. Коэффициент эксцесса
Коэффициент эксцесса определяется по формуле:( х Х )4
КЭ
n 1
x X
2
n 1
4
(8)
Дисперсия является моментом второго порядка.
Коэффициент асимметрии является моментом третьего
порядка.
Коэффициент эксцесса является моментом четвертого
порядка.
Лекция №1, ТВиМС, Лакман И.А.
17
18. Методы выборочного наблюдения
Определение: Выборочным несплошным наблюдением являетсянаблюдение, при котором признаки регистрируются у отдельных единиц
изучаемой совокупности, отобранных с помощью специальных методов.
Полученные в ходе выборочного наблюдения результаты распространяются
на всю исходную совокупность с заданным уровнем доверия.
Виды выборочного наблюдения:
1. Простая случайная (собственно-случайная) выборка
2. Систематическая (механическая) выборка
3. Стратификационная (типическая) выборка
4. Гнездовая (серийная) выборка
Отбор единиц в выборочную совокупность
Повторный отбор
Бесповторный отбор
Для
каждой
выборки
определяют
границы
генеральных
характеристики: средняя ошибка выборки, предельная ошибка
выборки. Определяют генеральную долю и необходимый объем
Лекция №3, Анализ даных Лакман И.А.
18
выборки.
19. Простая случайная выборка
Единицы выборки отбираются в случайном порядке, не зависящем ниот последовательности расположения единиц, ни от значения признаков
совокупности, не учитывают ни принадлежность к какой –либо группе, ни к
серии из единиц совокупности.
Средняя ошибка повторной выборки:
n
Где σ – среднее квадратическое отклонение изучаемого признака;
n – объем выборочной совокупности.
2
n
x
1
Средняя ошибка бесповторной выборки:
n N
Где σ – среднее квадратическое отклонение изучаемого признака;
n – объем выборочной совокупности.
N – объем генеральной совокупности.
Предельная ошибка выборки определяется на основе уровня
вероятности. При t=2 (p=0,954), t=3 (p=0,997), где t- статистика Стьюдента.
~x t ~x
~
~
x
x
x ~x
~
x
Генеральная средняя находится в интервале:
Лекция №3, Анализ даных Лакман И.А.
19
20. Простая случайная выборка
Необходимый объем простой случайной повторной выборки:n
t 2 2
2 ~x
Где σ – среднее квадратическое отклонение изучаемого признака;
~x – предельная ошибка выборки.
Необходимый объем простой случайной бесповторной выборки:
t 2 2 N
n
2 2 2~ N
t
x
Где σ – среднее квадратическое отклонение изучаемого признака;
~x - предельная ошибка выборки.
N – объем генеральной совокупности.
Полученный результат округляет в большую сторону от целого
значения
Лекция №3, Анализ даных Лакман И.А.
20
21. Стратификационная выборка
Единицы генеральной совокупности объединены в несколькотипических групп. И формирование выборки производится из единиц
каждой группы генеральной совокупности пропорционально их объему.
2
Средняя ошибка повторной выборки: n
Где – среднее из внутригрупповых дисперсий;
n – объем выборочной совокупности.
2
n
1
n N
Средняя ошибка бесповторной выборки:
Где – среднее из внутригрупповых дисперсий;
n – объем выборочной совокупности.
N – объем генеральной совокупности.
Лекция №3, Анализ даных Лакман И.А.
21
22. Стратификационная выборка
Необходимый объем стратификационной повторной выборки:t 2 2
n
2 ~x
Где – среднее из внутригрупповых дисперсий;
~x – предельная ошибка выборки.
Необходимый объем стратификационной бесповторной выборки:
n
Где
2
t 2 N
t 2 2 2 ~x N
– среднее из внутригрупповых дисперсий;
~x
– предельная ошибка выборки.
N – объем генеральной совокупности.
Полученный результат распределяют по типическим
пропорционально их численности:
N
ni n i
N
Где N i - объем i-ой группы, ni - объем выборки из i-ой группы.
Лекция №3, Анализ даных Лакман И.А.
группам
22
23. Серийная (гнездовая) выборка
Единицы генеральной совокупности объединены в несколькоравновеликих по объему групп (серий). Единицей отбора является серия, а
внутри серии проводится сплошной отбор ее единиц совокупности
2
Средняя ошибка повторной выборки: r
Где r – число отобранных серий;
δ– межгрупповая дисперсия.
2 r
1
r
Средняя ошибка бесповторной выборки:
R
Где r – число отобранных серий;
δ– межгрупповая дисперсия.
R – общее число серий.
xi x 2
2
Межгрупповая дисперсия:
r
Где xi - средняя i-ой серии;
х - общая средняя по всей выборочной совокупности.
Лекция №3, Анализ даных Лакман И.А.
23
24. Серийная (гнездовая) выборка
Необходимый объем серийной выборки:t 2 2
r
2 ~x
Где δ – межсерийная дисперсия;
~x – предельная ошибка выборки.
Необходимый объем серийной бесповторной выборки:
r
t 2 2 R
t 2 2 2~x R
Где δ – межсерийная дисперсия;
~x – предельная ошибка выборки.
R – общее число серий.
Лекция №3, Анализ даных Лакман И.А.
24
25. Систематическая ( механическая) выборка
Для систематической выборки отбирают единицы из генеральнойсовокупности через равные интервалы в соответствии с установленным
процентом отбора.
Характеристики систематической выборки определяются по тем же
самым формулам, что и для простой случайной выборки.
Лекция №3, Анализ даных Лакман И.А.
25






















 Математика
Математика








