Магнитное поле. Иллюстративный материал к лекции №12

1.

Магнитное поле
Иллюстративный материал к
лекции №12
пятница, 16 июня 2023 г.

2.

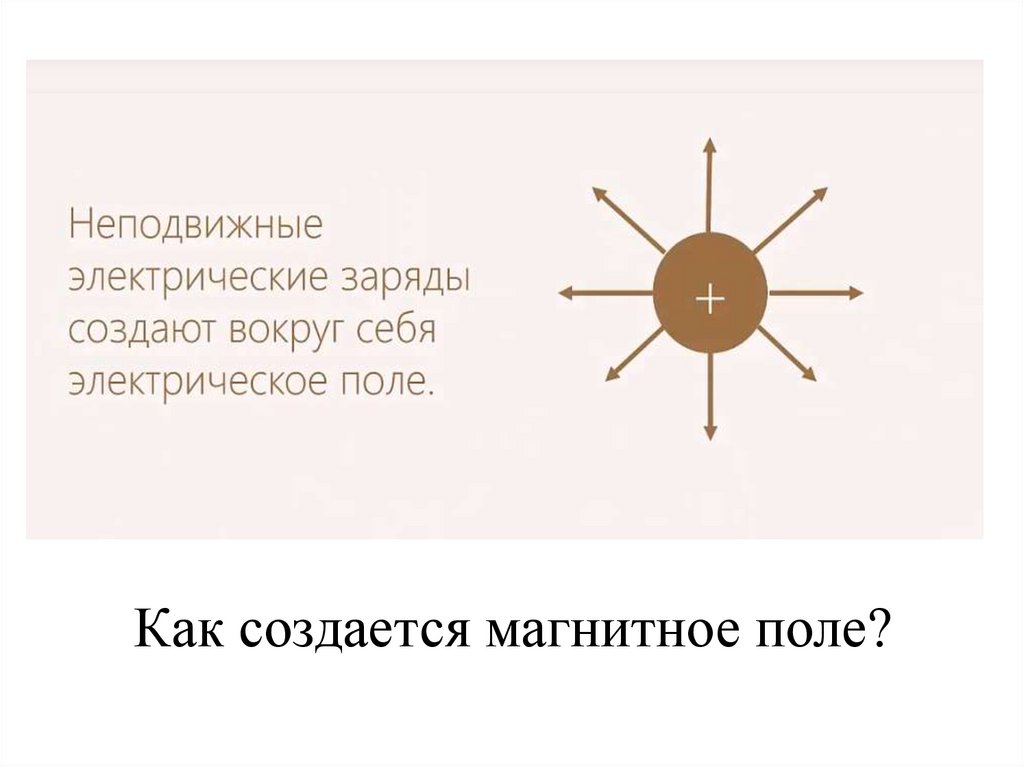
Как создается магнитное поле?

3.

Конечно, при помощи магнита!
Магнитные свойства известны человеку несколько тысяч лет

4.

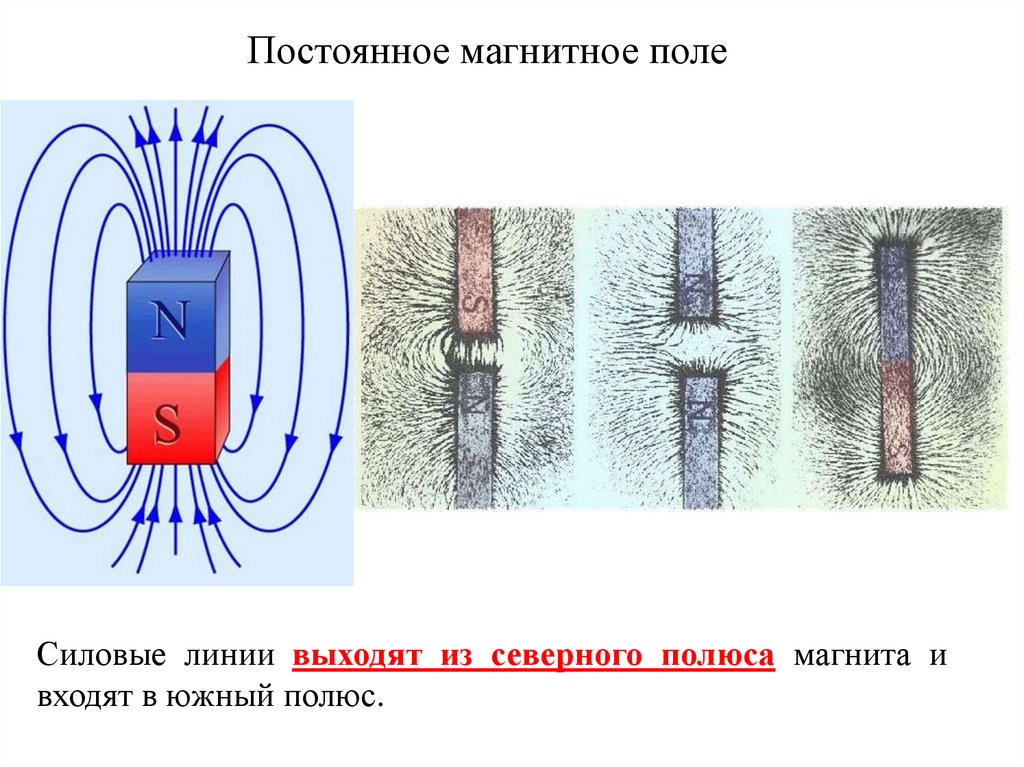
Постоянное магнитное поле
Силовые линии выходят из северного полюса магнита и
входят в южный полюс.

5.

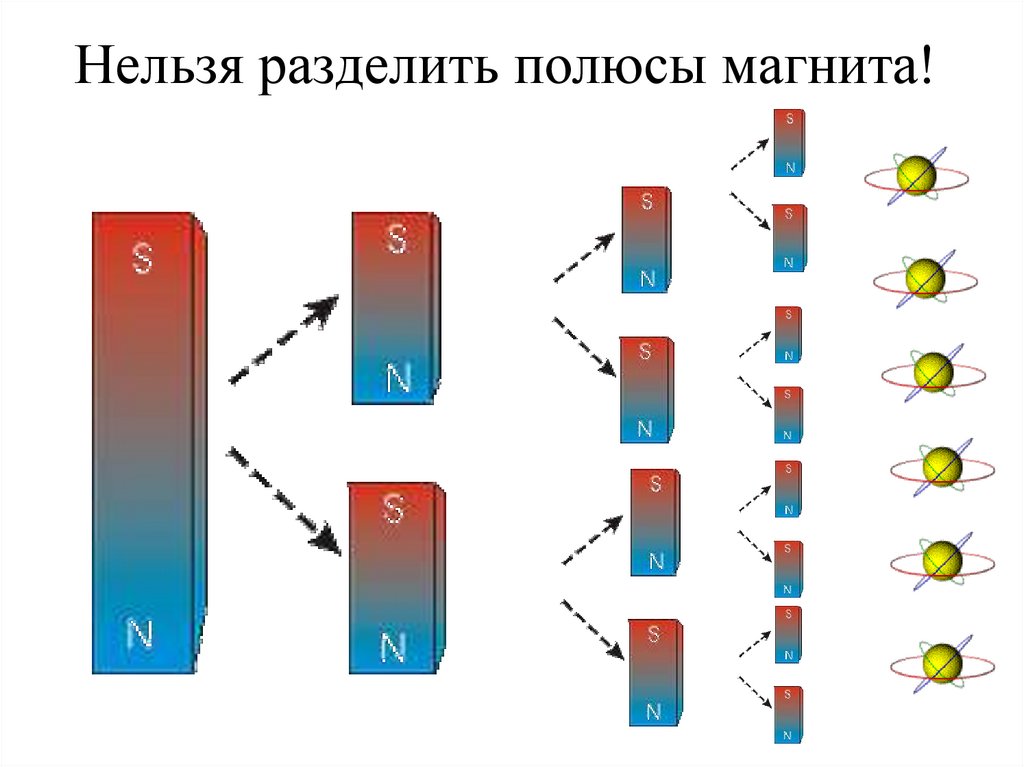
Нельзя разделить полюсы магнита!

6.

Магнит — тело, обладающее
собственным магнитным полем
Виды магнитов:
Природные магниты (магнитная
руда), образуются, когда руда,
содержащая железо или окиси
железа, охлаждается и
намагничивается за счет земного
магнетизма.
► Временные магниты — действуют
как постоянные магниты только
тогда, когда находятся в сильном
магнитном поле, и теряют свой
магнетизм, когда магнитное поле
исчезает(скрепки и гвозди).
► Электромагниты - металлический
сердечник с индукционной катушкой,
по которой проходит электрический
ток.

7.

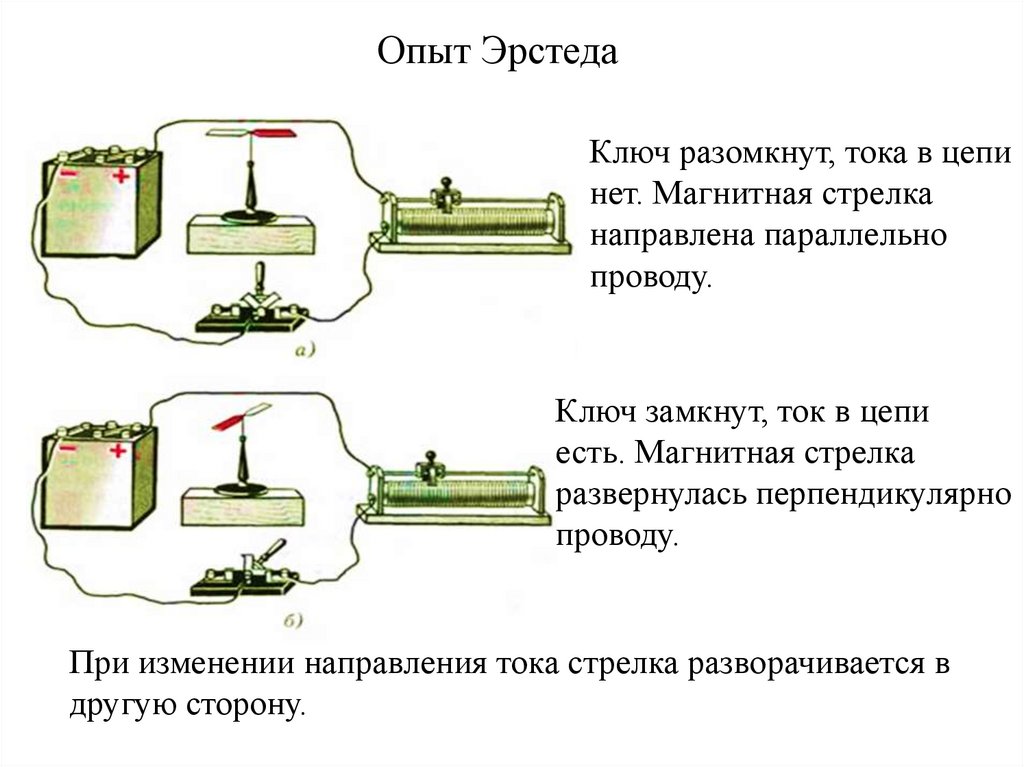
Опыт Эрстеда
Ключ разомкнут, тока в цепи
нет. Магнитная стрелка
направлена параллельно
проводу.
Ключ замкнут, ток в цепи
есть. Магнитная стрелка
развернулась перпендикулярно
проводу.
При изменении направления тока стрелка разворачивается в
другую сторону.

8.

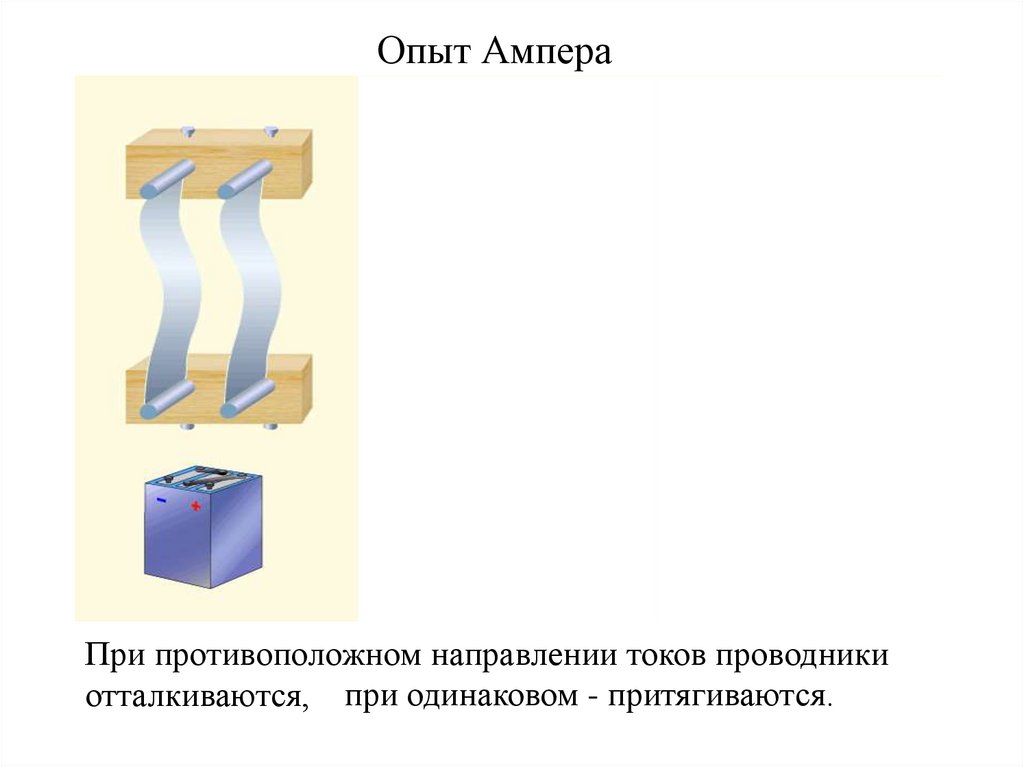
Опыт Ампера
При противоположном направлении токов проводники
отталкиваются, при одинаковом - притягиваются.

9.

Основные свойства магнитного поля:
• Магнитное поле является особой формой материи,
посредством которой осуществляется взаимодействие
между движущимися заряженными частицами.
• Магнитное поле порождается электрическим током
(движущимися зарядами). Вокруг неподвижного
заряда существует только электростатическое поле.
• Магнитное поле обнаруживается по действию на
электрический ток, то есть на движущиеся заряды.
• Магнитное поле при удалении от источника поля
ослабевает.

10.

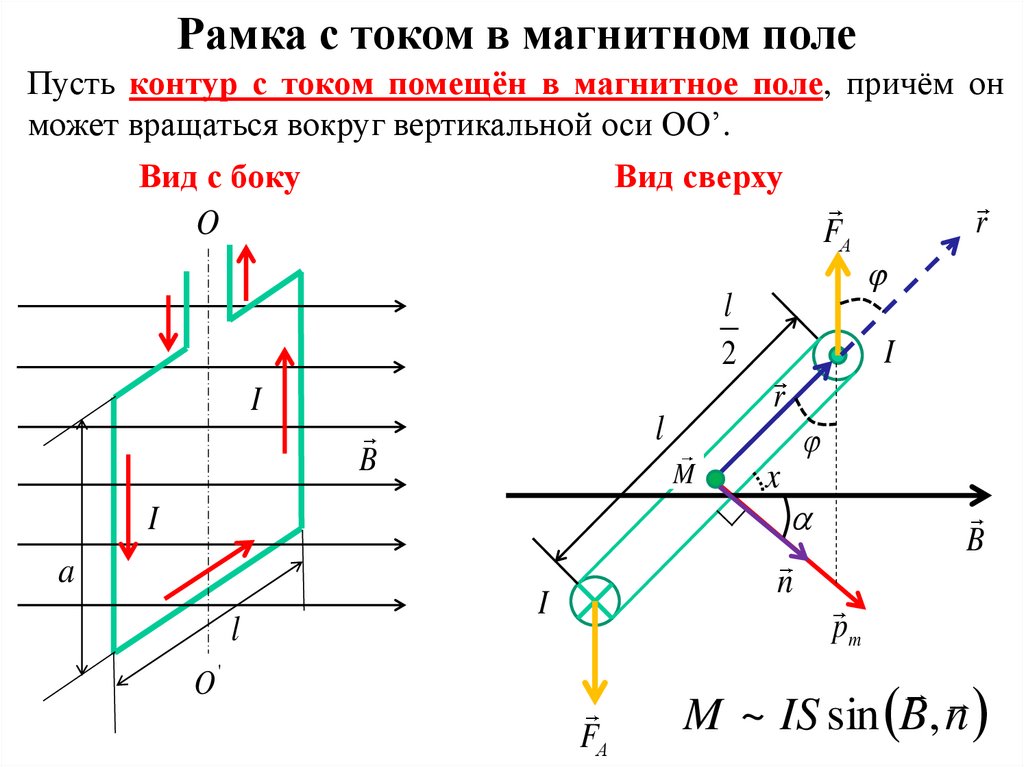
Рамка с током в магнитном поле
Пусть контур с током помещён в магнитное поле, причём он
может вращаться вокруг вертикальной оси OO’.
Вид сверху
Вид с боку
O
FА
l
2
I
r
I
l
B
M
I
a
l
r
x
B
n
I
pm
O'
FА
M ~ IS sin B, n

11.

Вектор магнитной индукции
Аналогии с электричеством:
Дипольный момент
Магнитный момент
p ql
pm IS
q аналог I
Отношение момента силы к магнитному моменту для данной
точки магнитного поля будет одним и тем же и может служить
характеристикой магнитного поля, названной магнитной
индукцией:
M
M макс
B
или B
pmsin ( B, n )
pm
Магнитная индукция характеризует силовое действие магнитного
поля на ток. Магнитная индукция – аналог
вектора
напряженности электрического поля: B аналог E

12.

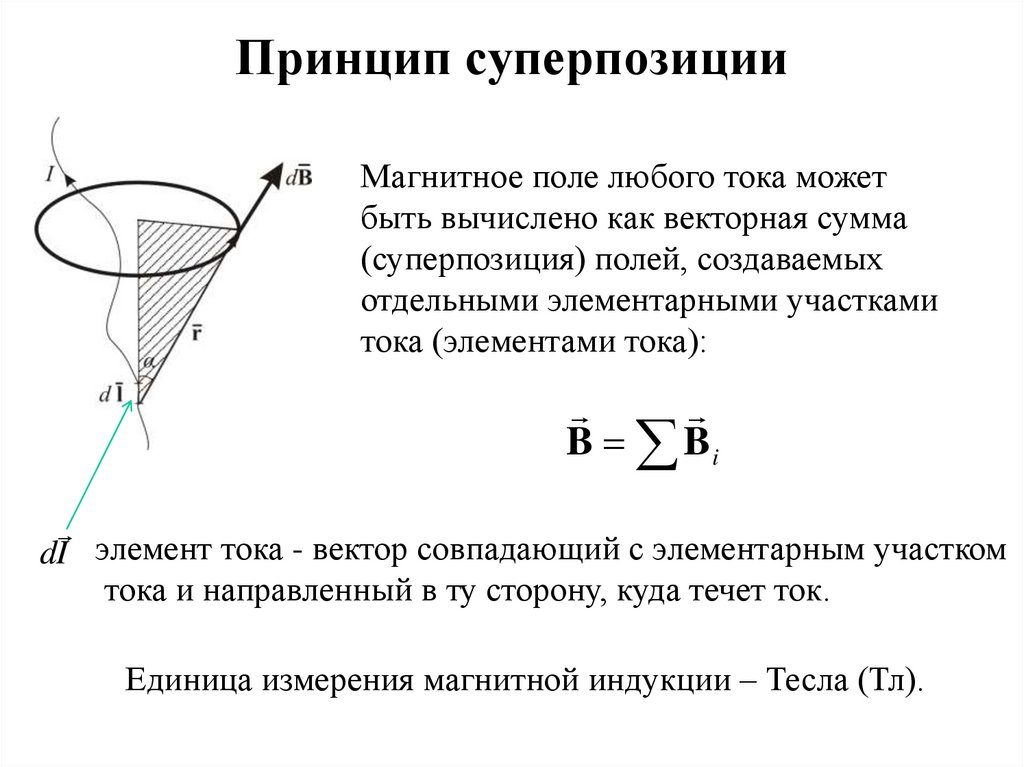
Принцип суперпозиции
Магнитное поле любого тока может
быть вычислено как векторная сумма
(суперпозиция) полей, создаваемых
отдельными элементарными участками
тока (элементами тока):
B Bi
dI элемент тока - вектор совпадающий с элементарным участком
тока и направленный в ту сторону, куда течет ток.
Единица измерения магнитной индукции – Тесла (Тл).

13.

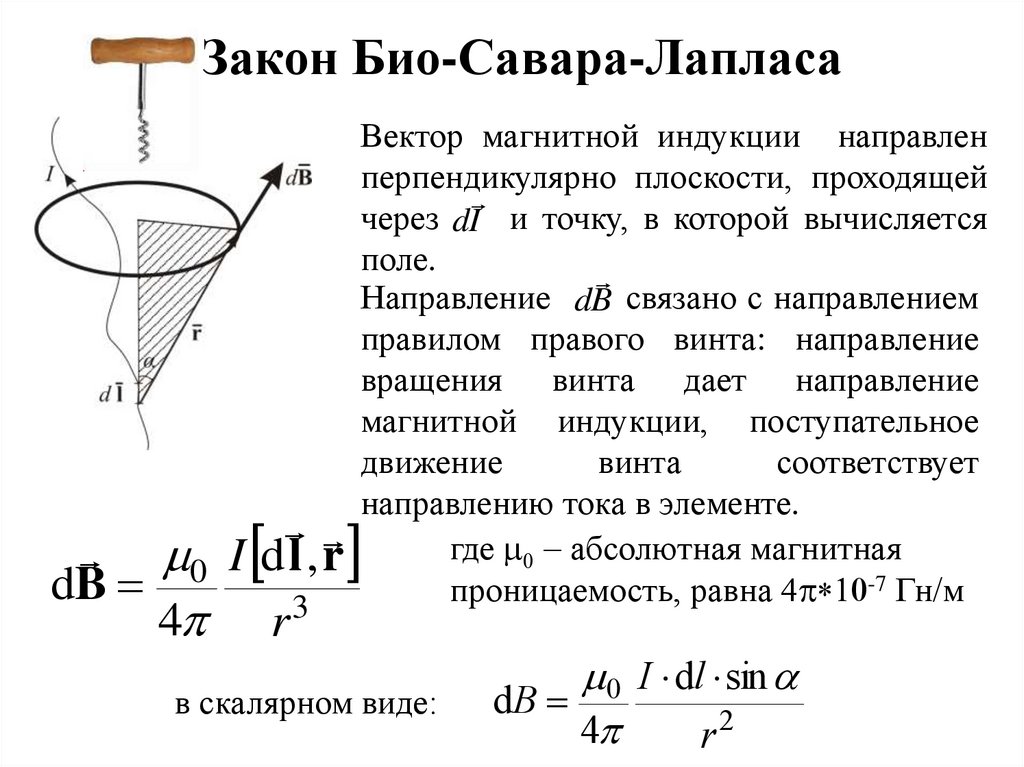
Закон Био-Савара-Лапласа
Вектор магнитной индукции направлен
перпендикулярно плоскости, проходящей
через dI и точку, в которой вычисляется
поле.
Направление dB связано с направлением
правилом правого винта: направление
вращения винта дает направление
магнитной индукции, поступательное
движение
винта
соответствует
направлению тока в элементе.
где 0 - абсолютная магнитная
0 I d l , r
-7 Гн/м
dB
проницаемость,
равна
4 *10
3
4
r
в скалярном виде:
0 I dl sin
dB
4
r2

14.

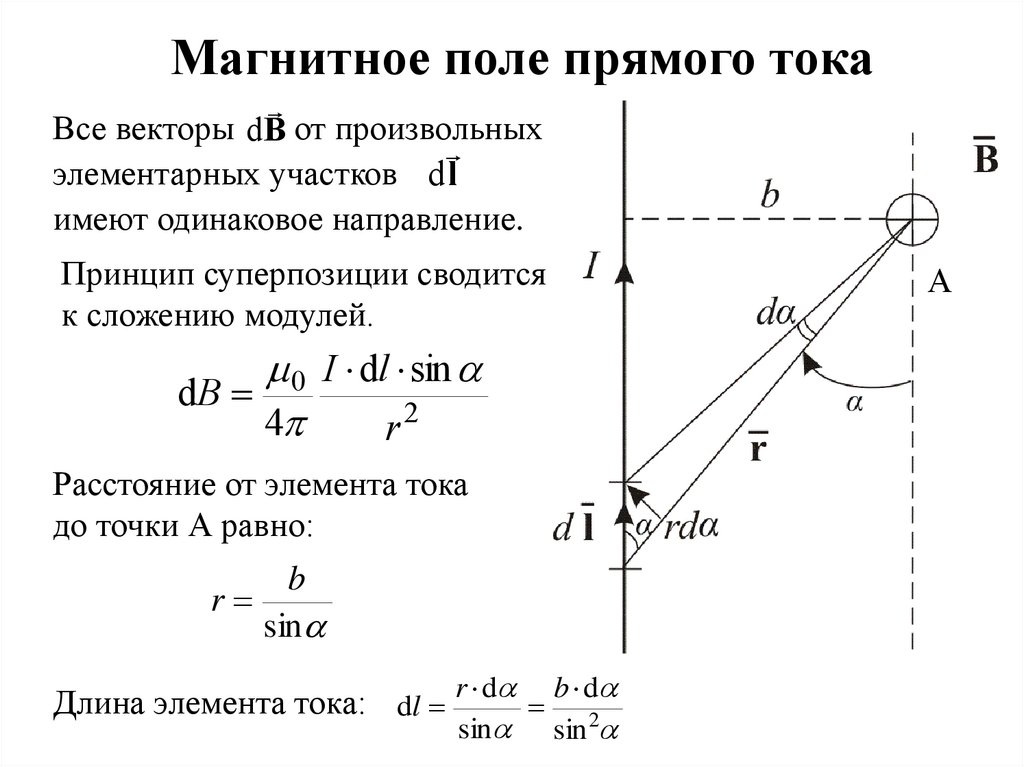
Магнитное поле прямого тока
Все векторы dB от произвольных
элементарных участков d l
имеют одинаковое направление.
Принцип суперпозиции сводится
к сложению модулей.
А
0 I dl sin
dB
4
r2
Расстояние от элемента тока
до точки А равно:
b
r
sin
Длина элемента тока: dl r d b d2
sin
sin

15.

Магнитное поле прямого тока
По закону Био-Савара-Лапласа получим:
Ib d sin sin I
dB
sin d
4
sin b
4 b
2
0
0
2
2
Для конечного проводника угол α изменяется от α1, до α2.
Тогда для конечного проводника:
2
2
0 I
0 I
cos 1 - cos 2
B dB
sin d
4 b
4 b
1
1
Для бесконечно длинного проводника
α1 = 0, а α2 = π и следовательно:
0 I
B
2 b

16.

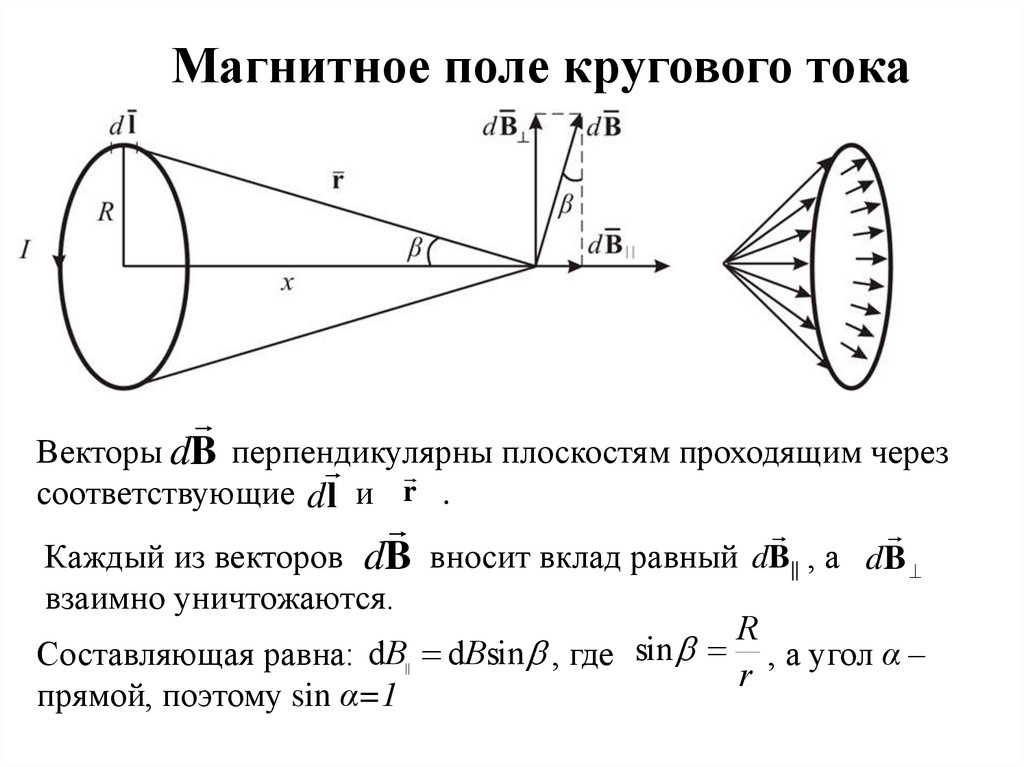
Магнитное поле кругового тока
Векторы dB перпендикулярны
плоскостям проходящим через
соответствующие d l и r .
Каждый из векторов dB вносит вклад равный dB|| , а dB
взаимно уничтожаются.
R
sin
Составляющая равна: dB dBsin , где
, а угол α –
r
прямой, поэтому sin α=1
||

17.

Магнитное поле кругового тока
По закону Био-Савара-Лапласа:
интегрируем
R 0 Idl R
dB|| dB
r 4 r 2 r
0 IR 2 R
0 2 R 2 I
B dB||
dl
3
4 R 2 x 2 32
4 r 0
где r R 2 x 2
Магнитная индукция в центре кругового тока:
B
0 I
2R

18.

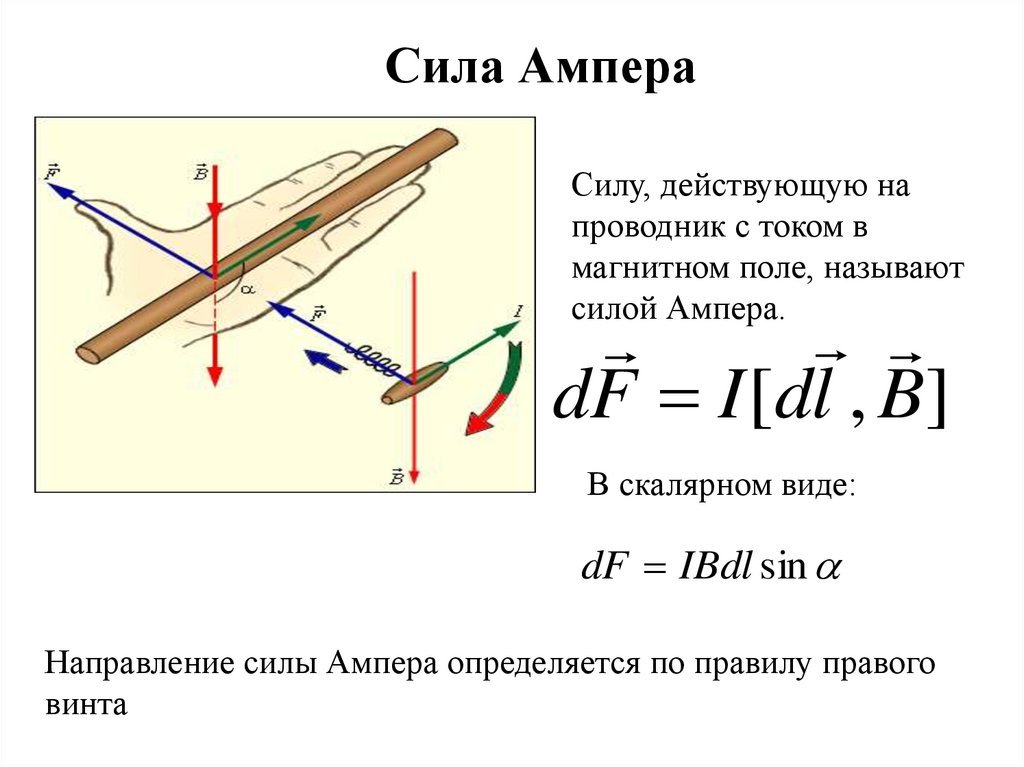
Сила Ампера
Силу, действующую на
проводник с током в
магнитном поле, называют
силой Ампера.
dF I [dl , B]
В скалярном виде:
dF IBdl sin
Направление силы Ампера определяется по правилу правого
винта

19.

Сила Лоренца
Сила Ампера равна:
dF I [dl , B]
Перепишем выражение для тока:
dl I jS dl
Получаем
Плотность тока
Idl jdV
jdV
dl
I
dF [ j , B]dV
Q qN
qN l qN
j
v
St St
S l t
dV
dF q[v , B]N
На 1 частицу:
F q[v , B]

20.

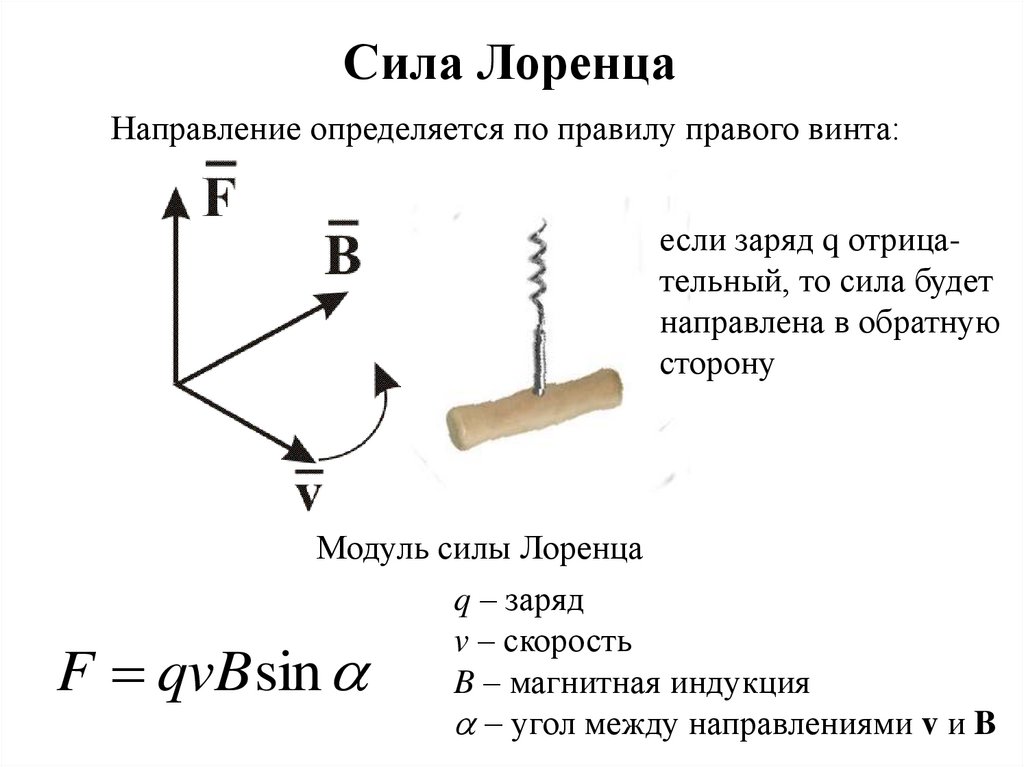
Сила Лоренца
Направление определяется по правилу правого винта:
если заряд q отрицательный, то сила будет
направлена в обратную
сторону
Модуль силы Лоренца
q – заряд
v – скорость
B – магнитная индукция
- угол между направлениями v и B
F qvB sin

21.

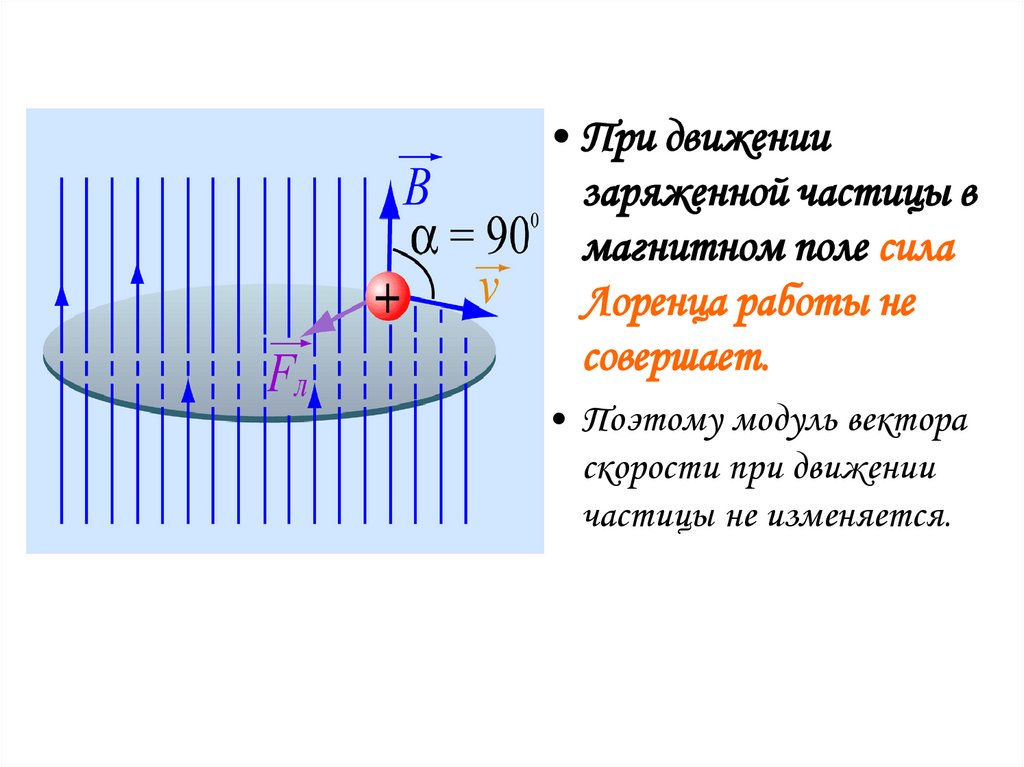
• При движении
заряженной частицы в
магнитном поле сила
Лоренца работы не
совершает.
• Поэтому модуль вектора
скорости при движении
частицы не изменяется.

22.

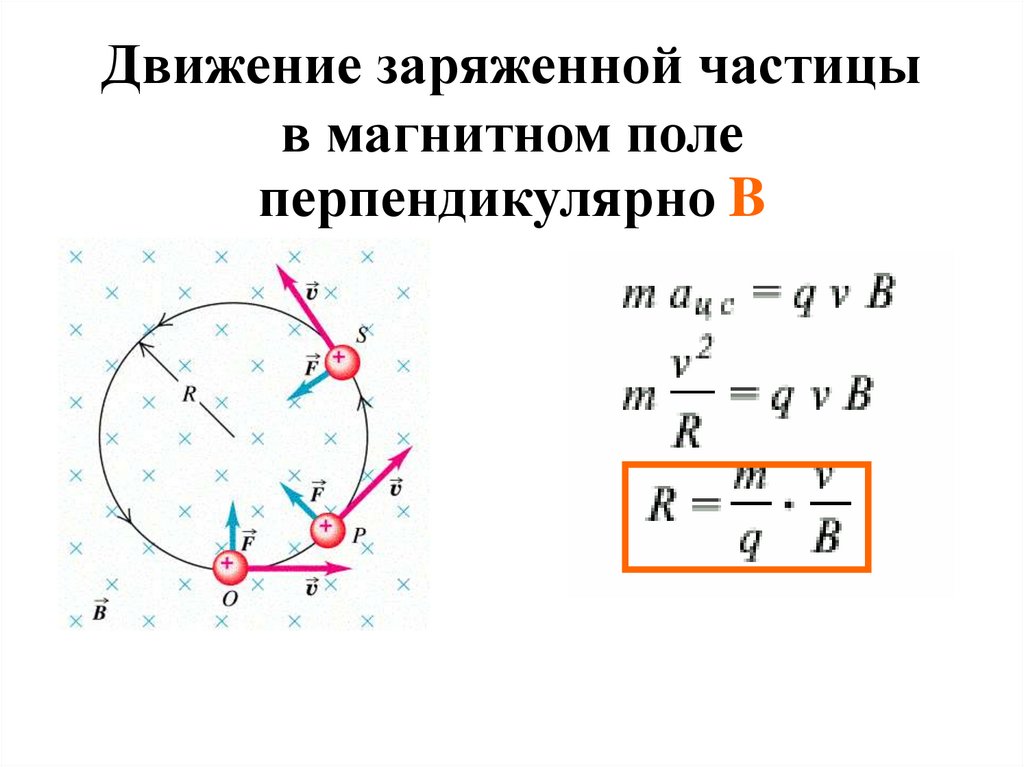
Движение заряженной частицы
в магнитном поле
перпендикулярно B

23.

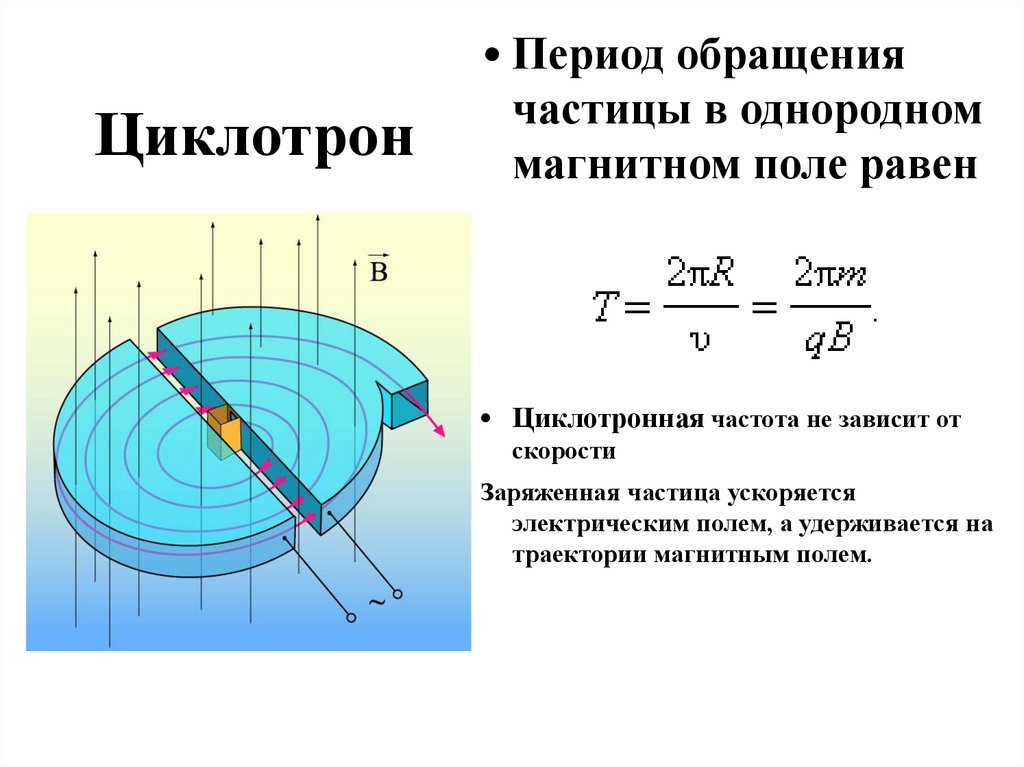
Циклотрон
• Период обращения
частицы в однородном
магнитном поле равен
• Циклотронная частота не зависит от
скорости
Заряженная частица ускоряется
электрическим полем, а удерживается на
траектории магнитным полем.

24.

Движение заряженной частицы
в магнитном поле под углом к B
• Такая частица будет двигаться
в однородном магнитном поле по
спирали.
• При этом радиус спирали R зависит от модуля
перпендикулярной магнитному полю
составляющей υ┴ а шаг спирали p – от модуля
продольной составляющей υ||

25.

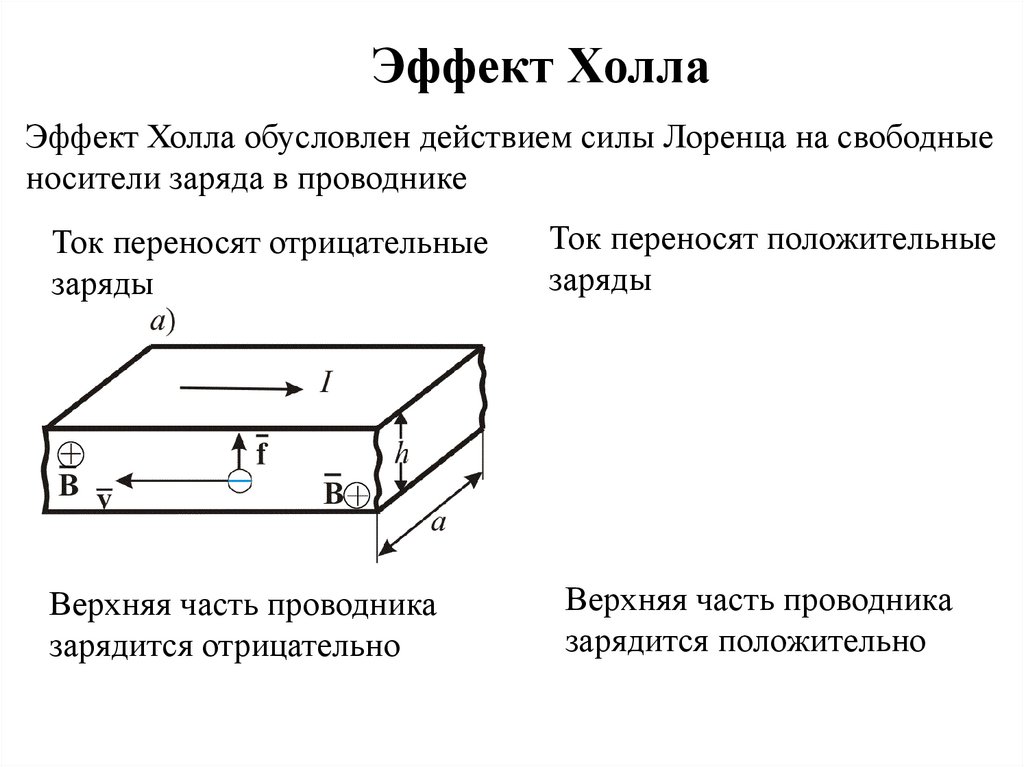
Эффект Холла
Эффект Холла обусловлен действием силы Лоренца на свободные
носители заряда в проводнике
Ток переносят отрицательные
заряды
Ток переносят положительные
заряды
Верхняя часть проводника
зарядится отрицательно
Верхняя часть проводника
зарядится положительно

26.

Эффект Холла
Подсчитаем величину Холловской разности потенциалов(Uх).
Обозначим Ex – напряженность электрического поля
обусловленного ЭДС Холла, h – толщина ленты проводника.
Ux = Ex h
Перераспределение зарядов прекратится когда сила q·Ex
уравновесит Лоренцеву силу, т.е.
q·Ex = q·B·υ или Ex = B·υ
j
j
Плотность тока j=n·υ·q отсюда
. Тогда E x B
.
nq
nq

27.

Тогда холловское напряжение Ux равно:
jBh
BhI
BI
Ux
или U x
nq
nqS qna
Измерив Ux , можно найти концентрацию носителей заряда:
.
IB
n
qaU x
Итак, измерение холловской разности потенциалов позволяет
определить: 1) знак заряда; 2) концентрацию носителей заряда