Магнитное поле. Лекция 12

1.

2.

3.

– одна из форм существования материи, создаваемая
движущимися электрическими зарядами (токами)
или постоянными магнитами.
Магнитное поле обнаруживается по действию на другие
магниты или токи (движущиеся электрические заряды).

4.

Силовой характеристикой магнитного поля
является
вектор магнитной индукции B .
Единица измерения магнитной индукции – Тесла (Тл).
Мощные магниты – В = 1-2 Тл.
Сверхпроводящие – В = 10 Тл.
Магнитное поле Земли – В = 0,5*10 -4 Тл.

5.

При исследовании магнитного поля используется
замкнутый плоский контур с током (рамка с током),
размеры которого малы по сравнению с расстоянием до
токов образующих магнитное поле.
В исследуемом магнитном поле на такой контур с током
будет действовать момент сил, заставляющий контур
поворачиваться определенным образом.

6.

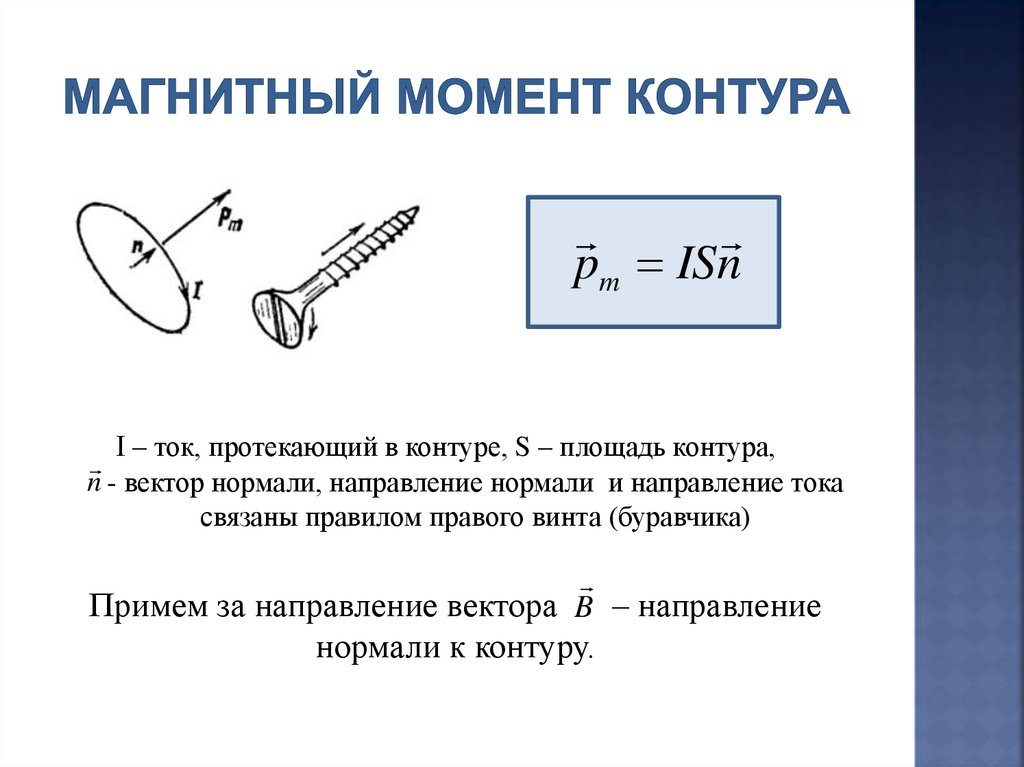
pm ISn
I – ток, протекающий в контуре, S – площадь контура,
n - вектор нормали, направление нормали и направление тока
связаны правилом правого винта (буравчика)
Примем за направление вектора B – направление
нормали к контуру.

7.

Если контур повернуть так, чтобы угол между нормалью контура и
направлением вектора B был равен 90о, то на контур будет
действовать максимальный по величине момент сил Мmax
Отношение момента силы к магнитному моменту для данной точки
магнитного поля не будет зависеть от магнитного момента
пробного тока и следовательно в качестве модуля магнитной
индукции можно принять величину:
M max
B
pm
Магнитная индукция B характеризует
силовое действие
магнитного поля на ток (аналогично, E характеризует силовое
действие электрического поля на заряд).

8.

Магнитные линии - это линии, касательные
к которым совпадают с
направлением вектора B в данной точке поля.
• линии магнитного поля замкнуты (вихревое поле);
• не пересекаются.

9.

Силовое воздействие магнитного поля (индукция магнитного поля)
зависит от свойств среды, в которой происходит взаимодействие.
Напряжённость магнитного поля H –
[H ] А
характеристика магнитного поля , которая
м
не зависит от свойств среды.
В случае изотропной среды индукция и напряженность магнитного
поля связаны соотношением
B 0 H
где µ – относительная магнитная проницаемость среды,
µ0 = 4 ·10-7 (Гн/м) – магнитная постоянная.

10.

Индукция магнитного поля,
созданная элементом
проводника dl в некоторой
точке равна:
I [dl r ]
dB 0
4 r 3
Модуль вектора магнитной
индукции можно вычислить по
формуле:
dB 0
Idl sin
4 r 2
I – сила тока, текущего в проводнике;
r – вектор, проведенный от элемента проводника dl в
точку, где мы определяем напряженность поля;
– угол между элементом проводника dl и вектором r.

11.

Если магнитное поле создается несколькими
токами,
то напряженность результирующего
поля H в любой точке равна векторной сумме
напряженностей H i , создаваемых каждым током
в отдельности:
n
H Hi
i 1

12.

13.

rd
dl
sin
R
r
sin
0 I
dB
sin d
4 R
B dB
0 I
0 2 I
sin
d
4 R
4 R
0

14.

Если ток течет по отрезку провода
0 I
B
(cos 1 cos 2 )
4 R

15.

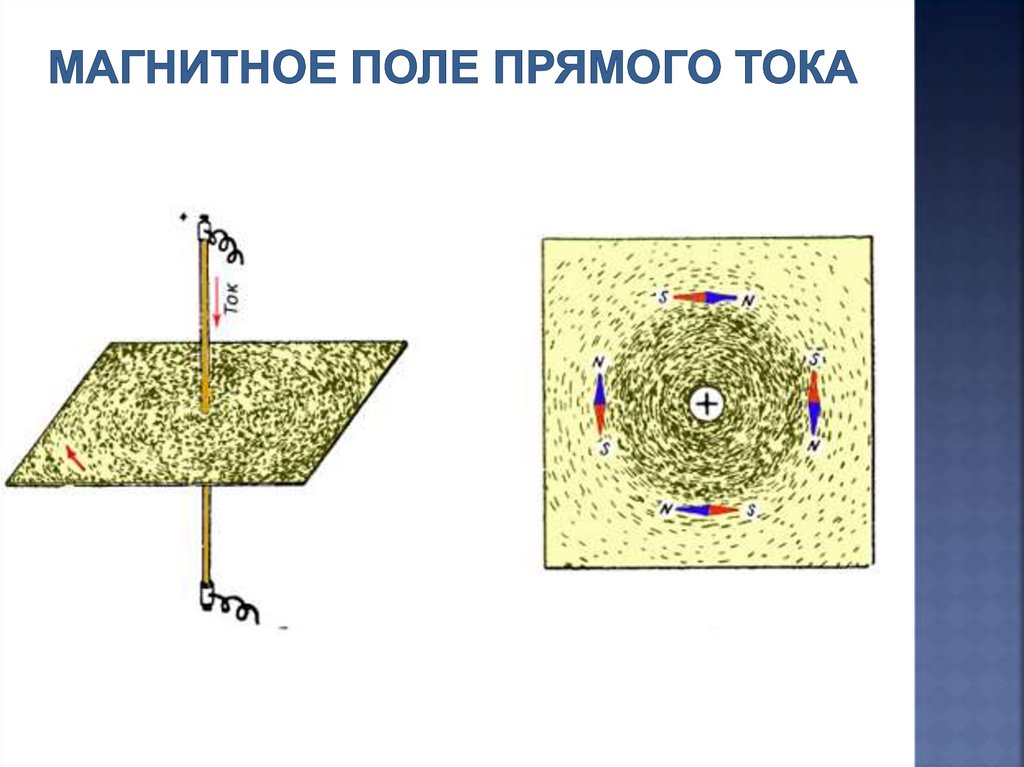
Напряженность магнитного поля
созданного бесконечным прямым
проводником с током
H
I
2 R
R– расстояние от тока до точки, в которой
определяется напряженность.
Напряженность магнитного поля
созданного отрезком прямого
проводника с током
R
H
I
4 R
(cos 1 cos 2 )
H

16.

17.

sin 1
r R
0 I
dB
dl
2
4 R
0 I
0 I
I
B dB
dl
2 R 0
2
2
4 R
4 R
2R
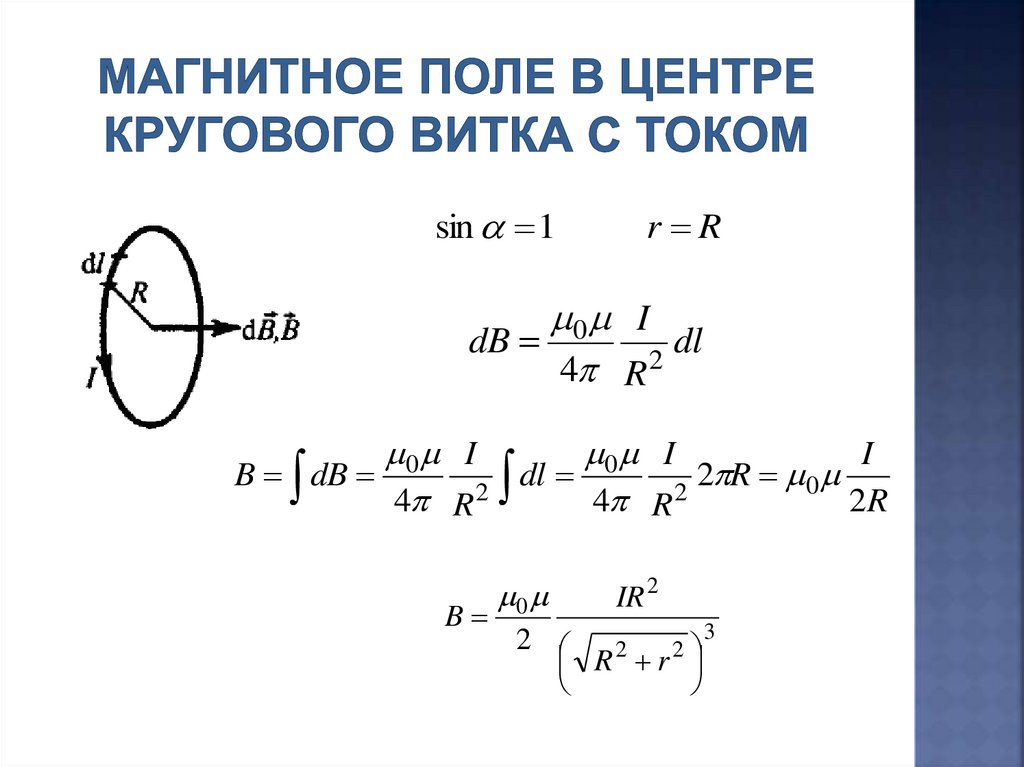
B
0
IR 2
3
2
2
2
R r

18.

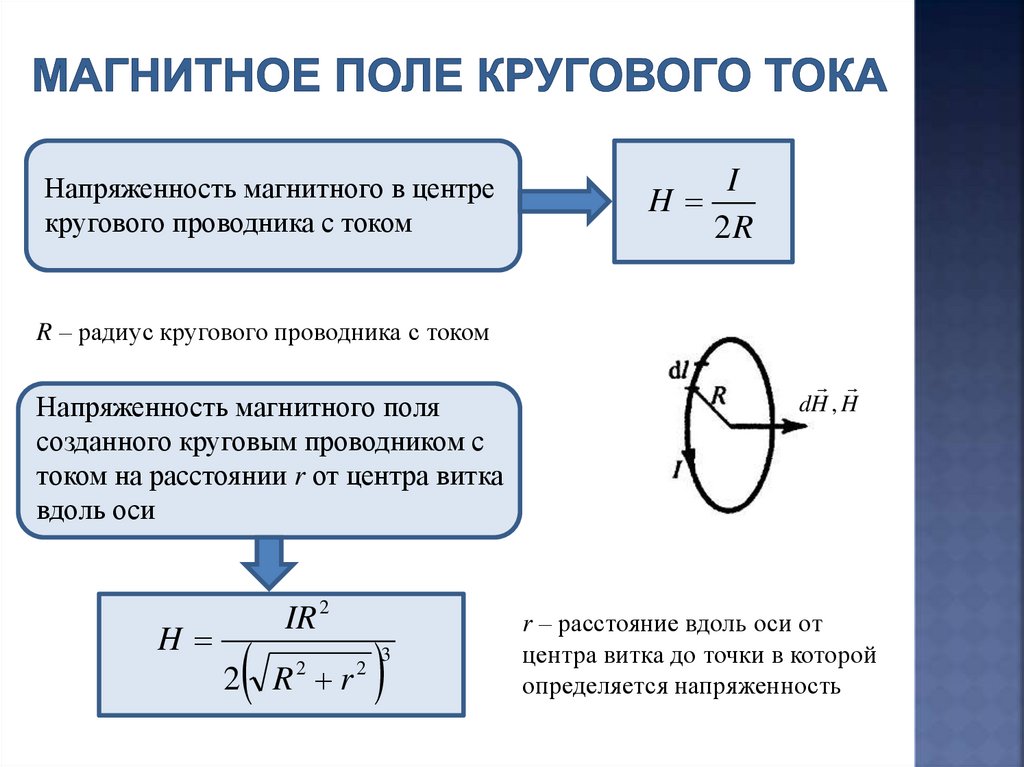
Напряженность магнитного в центре
кругового проводника с током
I
H
2R
R – радиус кругового проводника с током
Напряженность магнитного поля
созданного круговым проводником с
током на расстоянии r от центра витка
вдоль оси
H
IR 2
2 R r
2
2
3
dH , H
r – расстояние вдоль оси от
центра витка до точки в которой
определяется напряженность

19.

20.

А. Ампер установил, что на
каждый элемент проводника dl,
находящийся в магнитном поле,
действует сила:
dF I [dl B]
где dF – сила, действующая на элемент проводника ;
d l – элемент проводника;
B – поле в точке, где находится элемент dl .
Модуль силы Ампера, действующей на прямолинейный проводник,
находящийся в однородном магнитном поле, можно вычислить по
формуле:
F IBl sin
где α – угол между вектором B и направлением тока.

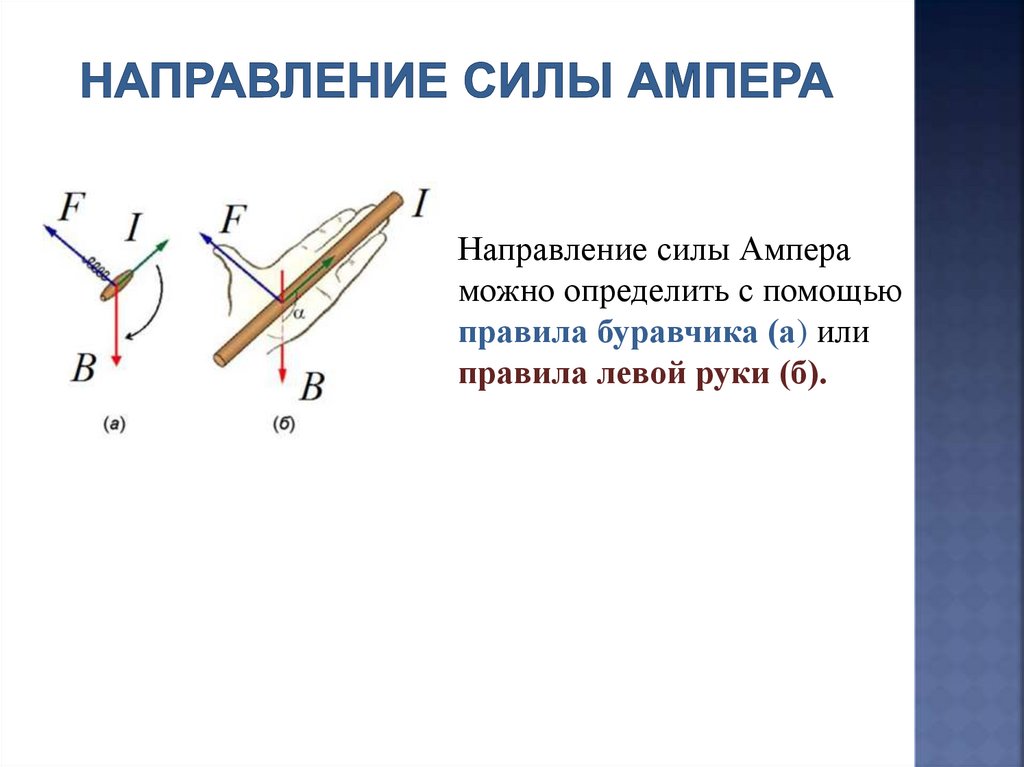
21.

Направление силы Ампера
можно определить с помощью
правила буравчика (а) или
правила левой руки (б).

22.

Сила взаимодействия двух параллельных проводников с током на
единицу длины проводника:
F 0 I1 I 2
l
2 R

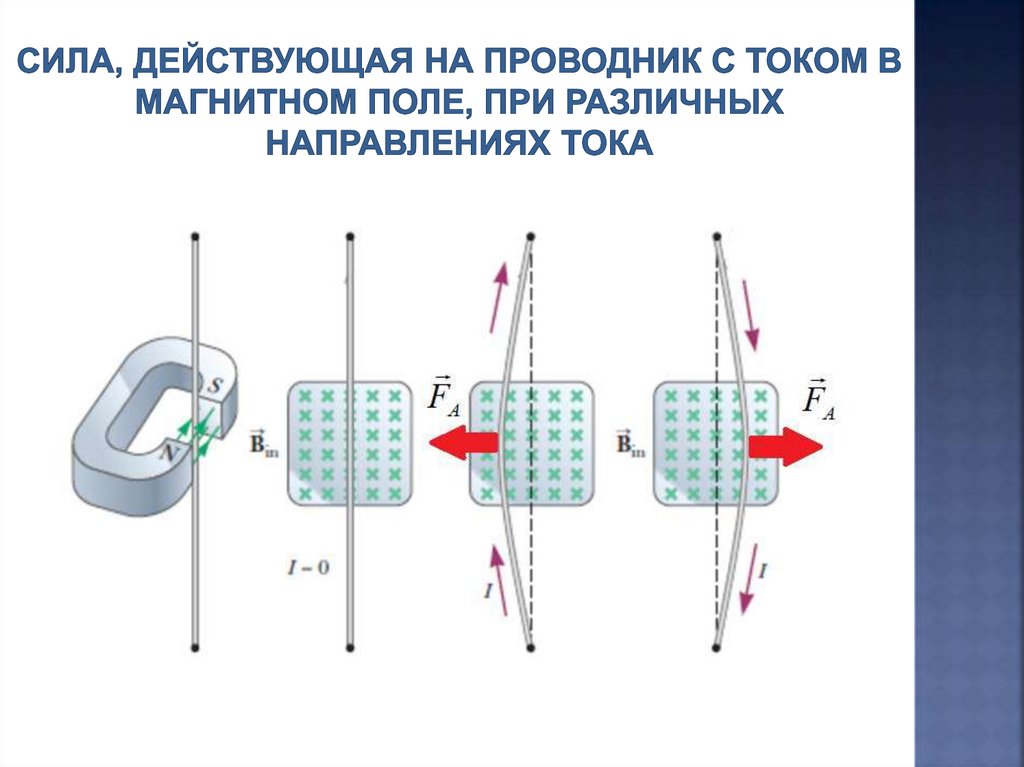
23.

На контур с током, помещенный в
магнитное поле, действует
вращающий момент
M ISB sin
На катушку с числом витков N,
помещенную в магнитное поле,
действует вращающий момент
M NISB sin

24.

B
V
Магнитное поле действует на, движущуюся со скоростью
заряженную частицу (заряд q) с силой Лоренца
F q[V B]
F qVB sin
B
V
где α – угол между векторами и
Направление силы определяется по правилу буравчика или по
правилу левой руки:

25.

26.

27.

28.

– это возникновение электрического поля в проводнике
или полупроводнике с током
при помещении его в магнитное поле
E R B, j
eE e
e B
a
Ba
а – ширина пластинки
e – заряд электрона
Δφ – поперечная (холловская) разность потенциалов

29.

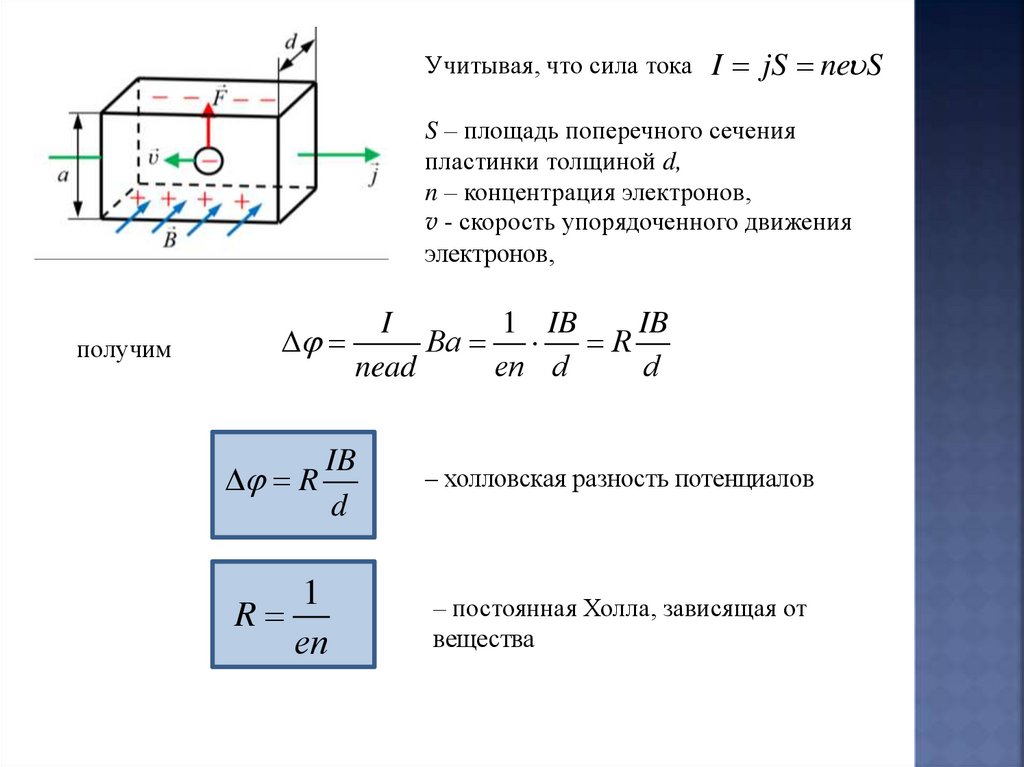
Учитывая, что сила тока
I jS ne S
S – площадь поперечного сечения
пластинки толщиной d,
n – концентрация электронов,
v - скорость упорядоченного движения
электронов,
получим
I
1 IB
IB
Ва
R
nead
еn d
d
IB
R
d
R
1
еn
– холловская разность потенциалов
– постоянная Холла, зависящая от
вещества

30.

измерение индукции магнитного
поля с помощью преобразователей
(датчиков) Холла
определение направления магнитного поля
по знаку постоянной Холла определяют тип
проводимости проводника или полупроводника: при
электронной проводимости R < 0; при дырочной
проводимости R > 0
по величине R можно определить концентрацию
носителей тока, если характер проводимости и их
заряд известны

31.

Циркуляцией вектора B по заданному замкнутому контуру L
называется интеграл
Bdl B dl
l
L
L
где dl – элемент длины контура, направленный
вдоль обхода контура;
Bl B cos - составляющая вектора B в направлении касательной к
контуру, с учетом выбранного
обхода;
направления
α - угол между векторами B и dl

32.

Циркуляция вектора магнитной индукции B по
произвольному замкнутому контуру L, равна µ0 умноженной
на алгебраическую сумму токов, охваченных этим контуром
Bdl I
0
охв .
L
L
Направление нормали к контуру
согласуется с направлением обхода
контура по правилу правого винта
(буравчика).
I
- сумма токов, охватываемых контуром.
Ток берется со знаком «+», если он направлен в ту же сторону, что и
нормаль и знак «-» в противоположном случае.
охв.
Для приведенного рисунка:
I
охв.
I1 I 2 I 3

33.

Теорема о циркуляции вектора B (закон полного
тока) справедлива только для поля в вакууме,
поскольку для поля
в веществе надо учитывать молекулярные токи.
Каждый ток учитывается столько раз, сколько он
охватывается контуром.
Положительным считается ток, направление
которого связано с направлением обхода по контуру
правилом правого винта.

34.

35.

36.

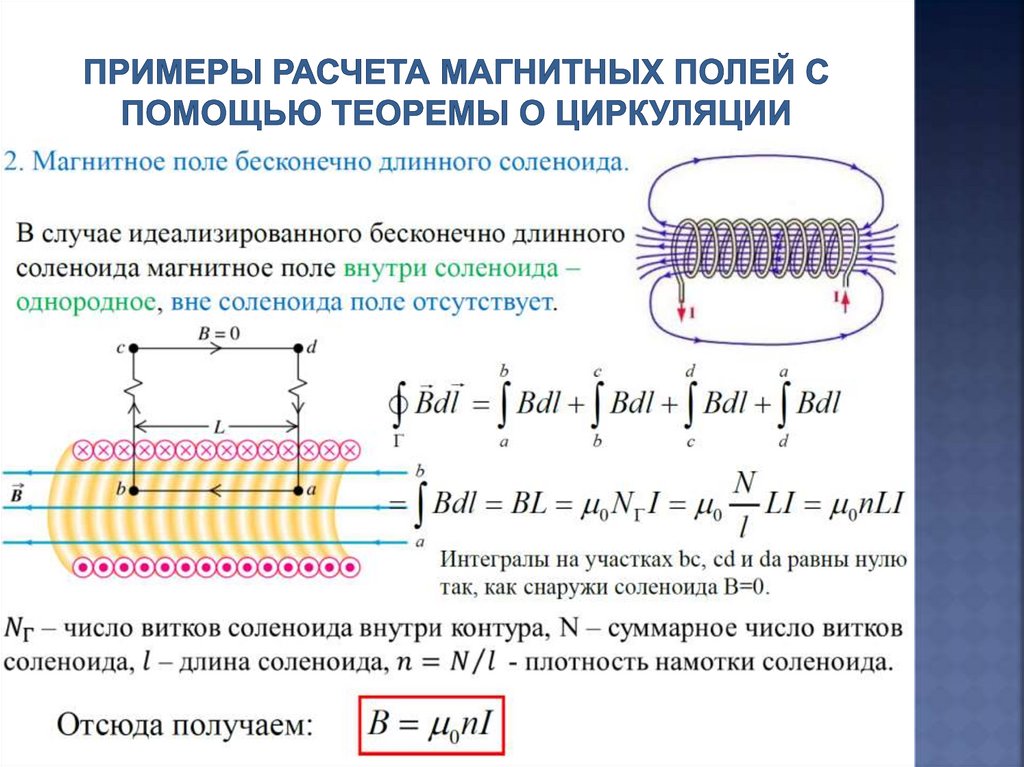
3. Магнитнитное поле тороида в вакууме
Тороидом – называется кольцевая катушка с
витками, намотанными на сердечник, имеющий форму
тора, по которой течёт ток.
Магнитное поле отсутствует вне тороида, а
внутри его оно является однородным.
Линии магнитной индукции, как следует из соображений симметрии,
есть окружности, центры которых расположены на оси тороида.
В качестве контура выберем одну такую окружность радиуса r .
По теореме о циркуляции
B 2 r 0 NI , где N – число витков тороида.
Следовательно,
0 NI
B
2 r

37.

Потоком вектора магнитной индукции ( магнитным потоком)
через площадку dS называется скалярная физическая величина,
равная
dФ BdS Bn dS
Bn B cos – проекция вектора B на направление нормали n
где
к площадке dS ;
α - угол между векторами n и B ;
равен dS, а направление совпадает
dS - вектор, модуль которого
направлением нормали n к площадке.
Положительное направление нормали к контуру связано с
направлением тока по правилу правого винта.

38.

ФB BdS Bn dS
S
S
Если поле однородно:
Ф BS cos

39.

1 Вб – магнитный поток, проходящий сквозь
плоскую поверхность площадью 1 м2 ,
расположенную перпендикулярно однородному
магнитному полю, индукция которого равна 1 Тл
1 Вб = 1Тл·м2

40.

Поток вектора магнитной индукции через любую замкнутую
поверхность S равен нулю.
BdS B ndS Bn dS 0
S
S
S
Здесь dS dS n , а n - вектор единичной нормали,
направленный наружу, из , объема, ограниченного
поверхностью S.
Bn - проекция вектора магнитной индукции на эту нормаль.

41.

Теорема гаусса для магнитного поля является отражением
экспериментального факта – замкнутости магнитных линий, т.е.
того, что магнитные линии не имеют ни начала ни конца.
Это означает, что:
В природе отсутствуют магнитные заряды!
Магнитное поле постоянного
магнита.
Электрическое поле двух
зарядов.
BdS 0
S
q
EdS 0
S
0

42.

Магнитный поток через поверхность, ограниченную
замкнутым контуром, называется потокосцеплением Ѱ
этого контура.
Потокосцепление контура, обусловленное магнитным
полем тока в самом этом контуре, называется
потокосцеплением самоиндукции.
Потокосцепление контура, обусловленное магнитным
полем тока, идущего в другом контуре, называется
потокосцеплением взаимной индукции этих
двух контуров.

43.

Найдём потокосцепление самоиндукции соленоида
с сердечником с магнитной проницаемостью μ.
Магнитный поток сквозь один виток соленоида
площадью S равен
Ф1 BS
Полный магнитный поток, сцепленный со всеми
витками соленоида, равен:
Ф1 N BSN
0 NI
l
N 2I
SN 0
S
l

44.

Проводник длиной l с током I
находится в однородном
магнитном
поле с индукцией B .
Под действием силы Ампера
проводник переместился из точки 1 в
точку 2
FА IBl
Работа, совершаемая магнитным полем:
dA Fdx I [l B]dx IBldx IBdS IdФ
dS ldx - площадь, пересекаемая проводником при его
перемещении в магнитном поле;
BdS dФ - поток вектора магнитной индукции пронизывающий эту
площадь.

45.

dA IdФ
Работа по перемещению проводника с током в магнитном
поле равна произведению силы тока на магнитный поток,
пересеченный движущимся проводником.

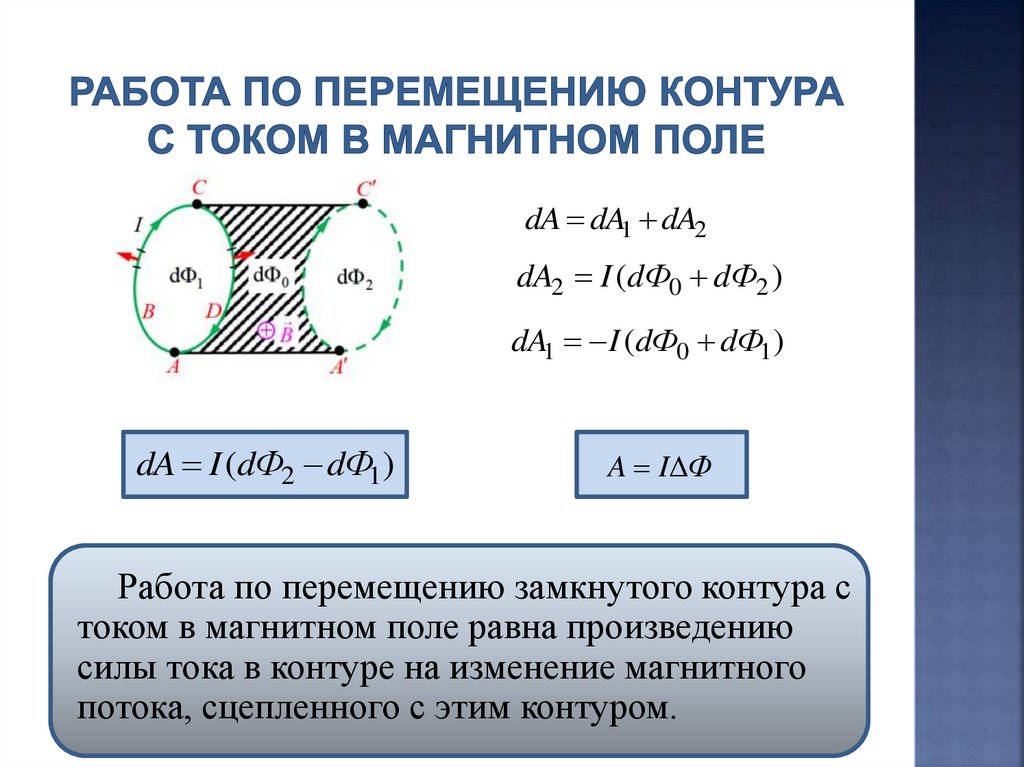
46.

dA dA1 dA2
dA2 I (dФ0 dФ2 )
dA1 I (dФ0 dФ1 )
dA I (dФ2 dФ1)
A I Ф
Работа по перемещению замкнутого контура с
током в магнитном поле равна произведению
силы тока в контуре на изменение магнитного
потока, сцепленного с этим контуром.

47.

Явление электромагнитной индукции
В замкнутом проводящем контуре при всяком
изменении магнитного потока, пронизывающего
его, возникает индукционный ток

48.

Индукционный ток возникает всегда, когда происходит
изменение сцепленного с контуром потока магнитной
индукции.
Сила индукционного тока не зависит от способа изменения
потока магнитной индукции, а определяется лишь скоростью
его изменения.
Открытие явления электромагнитной индукции:
показало взаимосвязь между электрическим и магнитным
полем;
предложило способ получения электрического тока с помощью
магнитного поля

49.

ЭДС электромагнитной индукции в контуре
численно равна и противоположна по знаку
скорости изменения магнитного потока сквозь
поверхность, ограниченную этим контуром
dФ
εi
dt
ЭДС электромагнитной индукции выражается в вольтах
2
Н м2
Дж А В с
dФ Вб Тл м
dt с с А м с А с А с В

50.

Индукционный ток, возникающий в контуре, имеет такое
направление, что его магнитное поле препятствует
изменению магнитного потока через поверхность,
ограниченную контуром.

51.

Согласно закону Фарадея, возникновение ЭДС электромагнитной
индукции возможно и в случае неподвижного контура, находящегося
в переменном магнитном поле.
Гипотеза Максвелла
Магнитное поле возбуждает в окружающем пространстве
вихревое электрическое поле, которое и является
причиной возникновения индукционного тока в проводнике.
Электрическое поле, возбуждаемое изменениями магнитного
поля, имеет непрерывные силовые линии, т.е. представляет собой
вихревое поле.
Циркуляция Е B этого поля по любому контуру L проводника
представляет собой ЭДС электромагнитной индукции
dФ
ε i E B dl
dt
L

52.

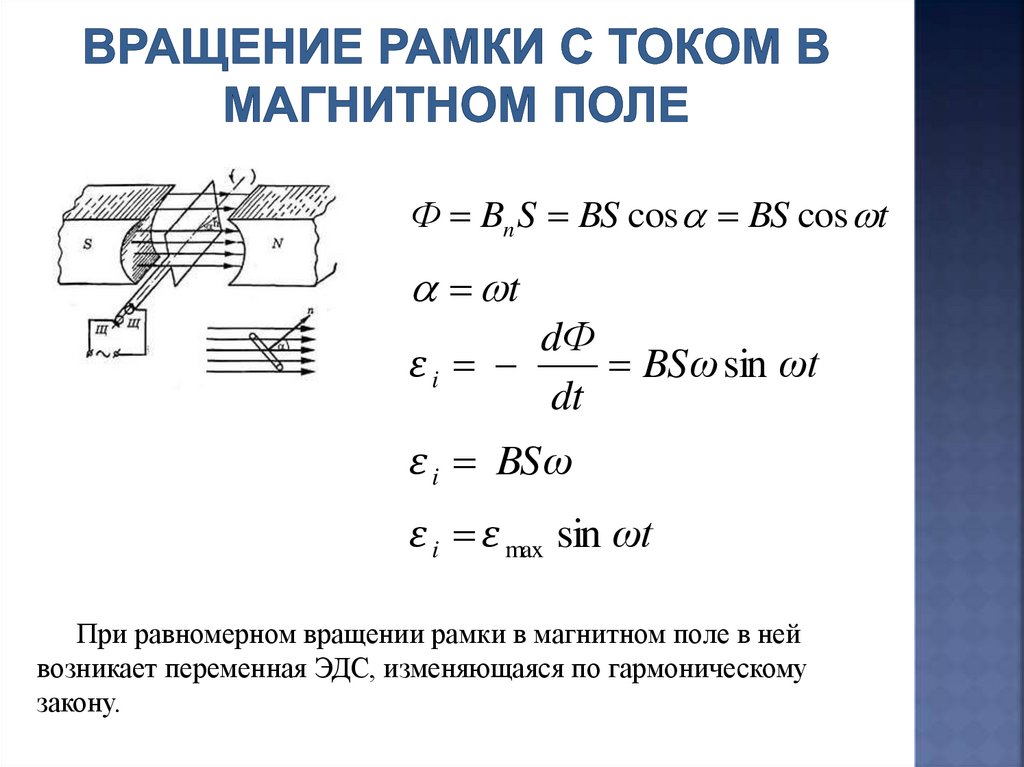
Ф Bn S BS cos BS cos t
t
dФ
εi
BSω sin ωt
dt
ε i BSω
ε i ε max sin ωt
При равномерном вращении рамки в магнитном поле в ней
возникает переменная ЭДС, изменяющаяся по гармоническому
закону.

53.

Электрический ток, текущий в замкнутом контуре, создает
вокруг себя магнитное поле, индукция которого, по закону Био –
Савара – Лапласа, пропорциональна току. Поэтому сцепленный
(связанный) с контуром магнитный поток пропорционален току в
контуре
Ф LI
где, коэффициент пропорциональности L называется
индуктивностью контура.
Индуктивность контура в общем случае зависит только от
геометрической формы контура, его размеров и магнитной
проницаемости той среды, в которой он находится.

54.

Магнитный поток через поверхность, ограниченную
замкнутым контуром называется потокосцеплением Ψ
этого контура.
Суммарный магнитный поток, связанный
(сцепленный) со всеми витками катушки, называется
потокосцеплением:
Фi
i
где Фi – магнитный поток через i-й виток.

55.

N – число витков соленоида,
l – его длина;
n=N/l – число витков, приходящихся на
единицу длины;
S – площадь поперечного сечения соленоида;
V – объем соленоида.

56.

dФ
d
ε is
LI
dt
dt
dI
ε is L
dt

57.

Пусть в цепи сопротивлением R и индуктивностью
L под действием внешней ЭДС ε течет постоянный
ток I0
I0
R
В момент времени t = 0 выключим источник тока.
Возникает ЭДС самоиндукции, препятствующая
уменьшению тока
dI
ε is L
dt
Ток в цепи определяется законом Ома
IR is

58.

IR L
dI
dt
Разделяем переменные:
dI
R
dt
I
L
И интегрируем по I (от I0 до I) и по t (от 0 до t):
I
R
ln t
I0
L
t
I I 0 exp
L
R
- постоянная, называемая
временем релаксации – время в
течение которого сила тока
уменьшается в e раз

59.

dI
ε is L
dt
IR is
dI
IR L
dt
t
I I 0 1 exp
I0 - установившийся ток (ток при t→ )

60.

Энергия магнитного поля равна работе, которую
затрачивает ток на создание этого поля.
LI 2
W
2
Объемная плотность энергии, т.е. энергия,
локализованная в единице объема V поля
dW 0 H 2
B2
BH
dV
2
2 0
2