Параллельное программирование. Занятие 10. Вычислители на основе модулярной арифметики

1.

РОССИЙСКИЙ ТЕХНОЛОГИЧЕСКИЙ
УНИВЕРСИТЕТ
МИРЭА
ПАРАЛЛЕЛЬНОЕ ПРОГРАММИРОВАНИЕ
Занятие 10. Вычислители на основе модуля́рной арифметики
(“система оста́точных классов”).
Баканов Валерий Михайлович, д.т.н., профессор
915-053-5469, 499-122-1328,
[email protected], http://vbakanov.ru/left_1.htm
Кафедра КБ-5 “Аппаратное, программное и математическое обеспечение вычислительных систем”

2.

Недостаток процесса вычислений в позиционной
системе счисления (ПСС)
2
Основная (т.к. с модификациями используется в качестве
составной части всех иных арифметических операций)
операция СЛОЖЕНИЕ выполняется в ПСС поразря́дно
(фактически последовательно) поби́тно (в двоичной
ПСС) от наиболее младшего бита к старшим в
соответствие с правилами выполнения логической
операции ИЛИ: 0+0=0, 0+1=1+0=1, 1+1=†0, где † “единица-убийца” (знак переноса – carry sign); символ †
как раз и говорит о необходимости переноса в старший
разряд.
Именно в этом заключается принципиальный недостаток такой сиcтемы – значение
разряда i+1 зависит от состояния всех (более младших) i разрядов результата
выполнения операции. А это значит, что простое распараллеливание (для повышения
скорости вычислений) на уровне машинных команд невозможно* ! Один из выходов из
такой ситуации – переход к непозиционной системе счисления (напр., на основе
чисел Фибоначчи или модуля́рной арифметики).
Идея довольно проста – использовать систему счисления, позволяющую выполнять
арифметические действия с максимальным распараллеливанием (размер гранулы
параллелизма – меньше арифметического действия!). В настоящее время считается более
перспективной как раз модуля́рная (основанная на счисле́нии остаточных классов)
арифметика (относится к непозиционным системам счисления).
*
Вообще говоря, известны схемотехнические и логические ухищре́ния (параллельный перенос,
матричная и табличная арифметика и т.п.), позволяющие в рамках ПСС значительно ускорить
арифметические операции, однако все они требуют весьма значительных аппаратных затрат
(серьёзного усложнения АЛУ процессора).

3.

История модулярной арифметики (МА)
3
В III в. н.э. китайский математик Сунь-Цзы загадал загадку: если некоторое число разделить
на 3, то в остатке получится 2, если разделить на 5 - остаток будет 3, на 7 - 2. Каково это
число? На решение задачи ушло около тысячелетия - только в 1247 г. другой китайский
учёный Цань Цзю-шао нашёл ответ. Математическая формулировка несложна (X – иско́мое
число, % - операция взятия остатка при целочисленном делении):
X%3=2;
X%5=3;
X%7=2 ||| Нам (обычно) достаточно 2-3 минут, чтобы сообразить - X=??10…
Общее решение этой так называемой китайской теоремы об оста́тках (КТО) искали
многие исследователи. Лишь в 1734 г. немецкий математик Л.Эйлер представил общее
доказательство КТО, а в 1801 г. Гаусс существенно развил его в своих знаменитых
"Арифметических исследованиях". В середине XX века, чешские учёные М.Валах и
А.Свобода на новом техническом уровне предложили использовать древнюю китайскую
идею. Они же создали и первые модулярные ЭВМ "Эпос" и "Эпос-2” (машины обладали
невысоким быстродействием и практически не использовались).
Если выполнять операции над числами не в привычной десятичной системе счисления,
а в системе с попарно взаимно простыми основаниями (модулями) над остатками чисел,
то появляется возможность сделать это более эффективно. Операции над вы́четами
(так называют остатки математики) по каждому модулю можно проводить независимо
и одновременно. Вводя дополнительные модули и получая таким образом избыточность,
обеспечивается контроль и исправление ошибок в процессе выполнения операций. Это
одно из важнейших преимуществ МА (арифметичность) перед любой позиционной
системой счисления. Ни одна из них не позволяет не находить, ни тем более исправлять
ошибки в процессе выполнения арифметических операций. Напротив, при возникновении
ошибок в арифметическом устройстве они далее бесконтрольно распространяются…

4.

Представле́ние чисел в
системе остаточных классов (СОК)
4
Говорят, что α есть остаток числа A по модулю p (иногда говорится, что A сравни́мо с α по
модулю p), если имеет место равенство
где
- целая часть частного A/p,
причём α – наименьший целый остаток от деления A на p. Часто это соотношение
записывают как α ≡ A (mod p).
Для представле́ния чисел в СОК необходимо выбрать т.н. систему оснований – множество
целых чисел p1, p2, … pn ; тогда число A может быть представлено следующим образом:
A=(α1, α2, … αn), где αi ≡ A (mod pi), i=1…n.
Если в произведении
все основания pi суть попарно взаимно-простые (не имеют общих делителей, кроме ±1; при
этом сами основания могут и не быть простыми *) числа, то между числами 0,1,2, … (P-1) и
представленными в СОК числами согласно A=(α1, α2, … αn) имеет место взаимнооднозна́чное соответствие.
В самом деле, раз основания p1=3, p2=5, p3=7 взаимно-простые числа, то P=3×5×7=105 и в
СОК можно представлять десятичные числа в диапазоне [0÷104]; при выходе за границы
[0÷(P-1)] нарушается взаимно-однозначное соответствие между представлением
чисел в позиционной системе счисления и СОК. Напр., (2,1,4)сок=1110, ибо 11%3=2,
11%5=1, 11%7=4. Задача китайского математика Сунь-Цзы также решается просто:
2310=(2,3,2)сок при той же системе оснований (3,5,7).
* Например, система оснований (ба́зис) из трёх чисел (29,31,32) обладает свойством
попа́рной взаимной простоты́ (ибо НОД(29,32)=1, НОД(29,31)=1, НОД(31,32)=1); хотя число
32 простым не является…

5.

Арифметические действия над числами в СОК
5
В COK арифметические действия над числами выполняются независимо по каждому основанию p1, p2, …
pn . Обозначив действие арифметики (сложение, умножение, вычитание) через , имеем в СОК при A=(α1,
α2, … αn) и B=(β1, β2, … β n) для A B=(γ1, γ2, … γn), где
(последнее выражение как раз и говорит, что в качестве цифры
результата берётся наименьший остаток); ограничением является необходимость нахожде́ния обоих
операндов и результата в диапазоне [0÷(P-1)], где P= p1 × p2 × … × pn . Операции неце́лого деления,
сравне́ния на “больше”/“меньше” и т.п. в СОК выполняются значительно сложнее, т.к.
требуют информации обо всём числе (а не только его составляющих по модулю).
Очевидно, что для расширения диапазона представления чисел в СОК следует увеличить число и/или
значение оснований (тогда возрастёт P = p1 × p2 × … × pn ). Напомним, что в СОК обрабатываются только
целые положительные числа (для представле́ния отрицательных чисел приходится прибегать к
ухищрениям); при использовании СОК для обработки чисел с плавающей точкой используют
известный приём представления таких чисел в виде порядка и мантиссы при их независимой
обработке.
Преимущества арифметики в СОК: возможность почти неограниченного расширения диапазона
представления чисел (путём увеличения числа и/или значения оснований и возможность
использования табличного метода при (параллельном!) выполнении арифметических операций
(т.к.
отдельные
действия
производятся
над
числами
малой
величины).
СОК-арифметика
удивительно удобна для проведе́ния операций в современных криптографических системах!

6.

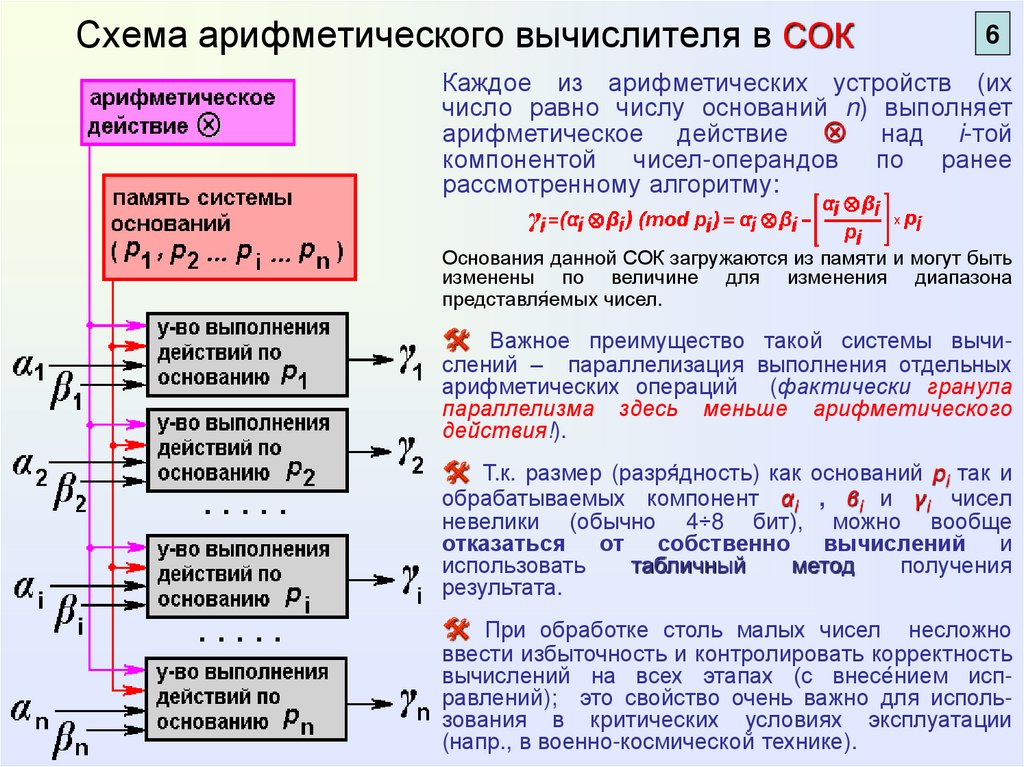
Схема арифметического вычислителя в СОК
6
Каждое из арифметических устройств (их
число равно числу оснований n) выполняет
арифметическое действие над i-той
компонентой чисел-операндов по ранее
рассмотренному алгоритму:
Основания данной СОК загружаются из памяти и могут быть
изменены по величине для изменения диапазона
представля́емых чисел.
Важное преимущество такой системы вычислений – параллелизация выполнения отдельных
арифметических операций (фактически гранула
параллелизма здесь меньше арифметического
действия!).
Т.к. размер (разря́дность) как оснований pi так и
обрабатываемых компонент αi , βi и γi чисел
невелики (обычно 4÷8 бит), можно вообще
отказаться от собственно вычислений и
использовать
табличный
метод
получения
результата.
При обработке столь малых чисел несложно
ввести избыточность и контролировать корректность
вычислений на всех этапах (с внесе́нием исправлений); это свойство очень важно для использования в критических условиях эксплуатации
(напр., в военно-космической технике).

7.

Уровни параллелизма в современных
вычислительных системах (1)
№
№
Общепринятое
наименование
1
Параллелизация на уровне
битов
Описание
технологии, уровень
гранулярности
В каких вычислительных
архитектурах применяется
Выполнение
всех
битовых операций над
двоичным
представлением чисел независимо
(т.е.
параллельно).
Фактически
идеализация
(хотя
известны
реализации
для
арифметических спецпроцессоров
для
выполнения
узкой
направленности действий – напр.,
быстрое преобразование Фурье). В
Мелкогрануля́рный
(fine-grained)
параллелизм
2
Параллелизация на уровне
машинных
команд (ILP –
InstructionLevel
Parallelizm)
7
реальности наиболее близко подошли́
к идеалу вычислители на основе
Системы Остаточных Классов (СОК)
разрабатывавшиеся
группой
И.Акушского в СССР на рубеже 60-70
годов
Выполнение
машин- Типичный пример – классический
ных команд (инструк- пото́ковый (DATA-FLOW) вычислиций) независимо (т.е. тель, векторные процессоры
параллельно)
Мелкозерни́стый
(fine-grained)
параллелизм

8.

Уровни параллелизма в современных
вычислительных системах (2)
№
№
Общепринятое
наименование
3
Параллелизация на уровне
потоков
Описание
технологии, уровень
гранулярности
8
В каких вычислительных
архитектурах применяется
Выполнение програм- Процессорная
многопоточность,
мных потоков незави- пользовательские
и
системные
симо (т.е. параллель- программы, операционные системы
но).
Среднезерни́стый
(medium-grained)
параллелизм
4
Параллелизация на уровне
заданий
Выполнение
заданий Операционные системы, многопро(задач) независимо (т.е. цессорные и многокомпьютерные
параллельно)
вычислительные системы
Крупногрануля́рный
(coarse-grained)
параллелизм

9.

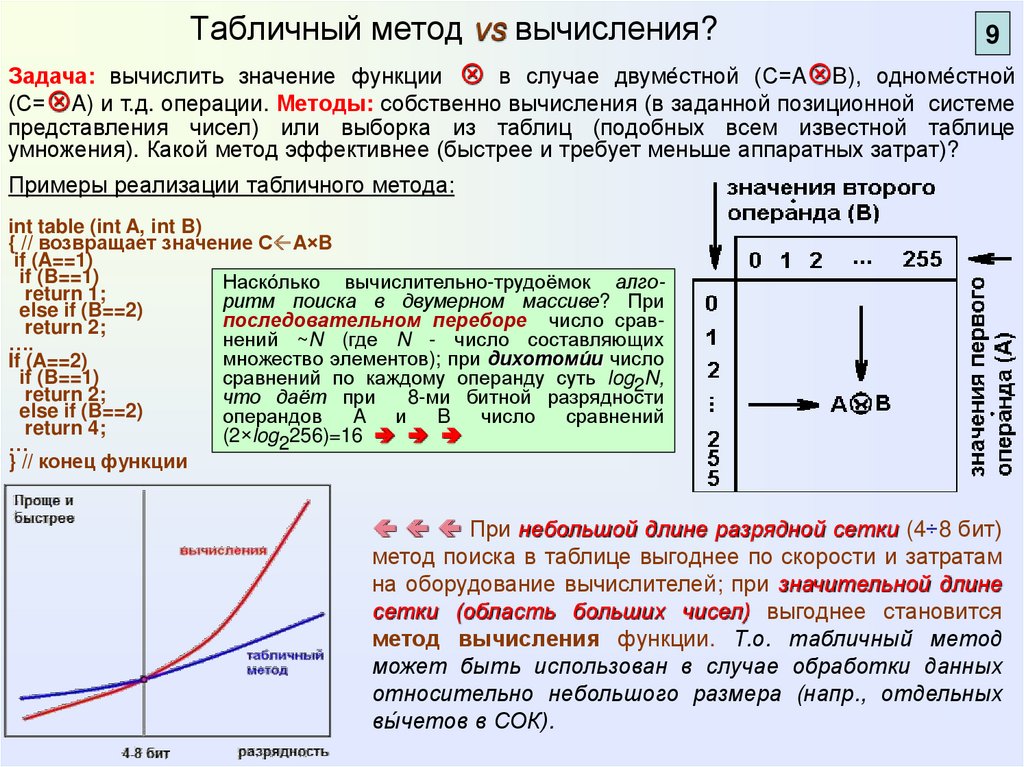
Табличный метод vs вычисления?
9
Задача: вычислить значение функции в случае двуме́стной (С=A B), одноме́стной
(С= A) и т.д. операции. Методы: собственно вычисления (в заданной позиционной системе
представления чисел) или выборка из таблиц (подобных всем известной таблице
умножения). Какой метод эффективнее (быстрее и требует меньше аппаратных затрат)?
Примеры реализации табличного метода:
int table (int A, int B)
{ // возвращает значение С A×B
if (A==1)
if (B==1)
Наско́лько вычислительно-трудоёмок алгоreturn 1;
ритм поиска в двумерном массиве? При
else if (B==2)
последовательном переборе число сравreturn 2;
нений ~N (где N - число составляющих
….
множество элементов); при дихотоми́и число
If (A==2)
if (B==1)
сравнений по каждому операнду суть log2N,
return 2;
что даёт при
8-ми битной разрядности
else if (B==2)
операндов
A и
B
число
сравнений
return 4;
(2×log
256)=16
2
…
} // конец функции
При небольшой длине разрядной сетки (4÷8 бит)
метод поиска в таблице выгоднее по скорости и затратам
на оборудование вычислителей; при значительной длине
сетки (область больших чисел) выгоднее становится
метод вычисления функции. Т.о. табличный метод
может быть использован в случае обработки данных
относительно небольшого размера (напр., отдельных
вы́четов в СОК).

10.

Вычислительные системы на основе СОК
10
Идея создания вычислителя на основе СОК возникла у И.Я.Акушского в
1954÷1956 г.г. как результат поисков методов,
позволяющих ускорить вычислительный процесс в ЭВМ; его поддержал акад. М.Лаврентьев, знакомый с
работами чехов М.Валаха и А.Свободы. В 1957 г. коллектив разработчиков СКБ245 в составе Ю.Базилевского, Б.Рамеева, Ю.Шрейдера и И.Акушского начал
работы по созданию ЭВМ в СОК с рекордной производительностью - более 1 млн.
операций в секунду (в то время производительность ЭВМ равнялась дес. тыс.
опер./сек). После завершения проекта А-340А возглавляемый Д.Юдицким
коллектив в 1960-1963 г.г. создал первую в стране (а возможно, и в мире) реально
работавшую модуля́рную ЭВМ Т-340А для полигонного варианта РЛС “Дунай3УП” системы ПРО А-35. В 1967÷1972 г.г. была разработана ЭВМ 5Э53
производительностью 40 млн. опер./сек!
ЭВМ Т-340А и К-340А обладали огромным для своего
времени быстродействием в 1,2 млн. двойных (2,4 млн.
обычных) оп./сек и min стоимостью единицы
производительности (25 коп. на оп./сек), работали с 45битной разрядностью данных и команд и системой
оснований p=(2,5,23,63,17,19,29,13,31,61), при этом
диапазон целых от 0 до 3’336’597’244’88910 (все вы́четы
укладываются в 6 двоичных разрядов) и обеспечивали
обнаружение ошибки в слове при выполнении операций.
Теория и практика варианта модулярной арифметики,
принципы построения ЭВМ на их основе были
предложены И.Акушским, Д.Юдицким и Е.Андриановым.
Благодаря
высочайшей
надёжности
и
уникальным
характеристикам ЭВМ К-340А находились в эксплуатации
минимум до 2005 г. (40 лет!), демонстрируя значительно
более высокую живучесть, чем работающие рядом с ними
другие, современные электронные системы.

11.

Проблемы ЭВМ с процессорами на основе СОК
11
Как и всё в нашем мире, ЭВМ с СОК-вычислителями, кроме ясно ви́димых преимуществ,
обладают и недостатками (часть из них ранее показана). Один из недостатков –
относительная громоздкость перевода чисел из СОК в позиционное представле́ние (вряд
ли все внешние устройства ЭВМ будут работать в СОК – это, в первую очередь, прерогатива
собственно арифметических вычислителей - процессоров).
Формула перевода чисел из СОК в позиционную десятичную систему счисления имеет
вид:
A10 = a1 × B1 + a2 × B2+ … +an × Bn – r × P,
где a1, a2, …, an - представление числа А в СОК с основаниями p1, p2, … pn;
P = p1 × p2 × … × pn;
r = 0,1,2,… целые числа, причём r выбирается таким образом, чтобы
между левой и правой частью выражения была меньше P;
разность
Bi = (P / pi) × ki, где ki = 1,2, … pi, причём ki выбирается так, чтобы остаток от деления
Bi / pi был равен 1.
Вышеприведённое выражение громоздко (а
значит, имеет повышенную вычислительную
сложность), но его необходимо использовать
всякий
раз,
когда
вычисленные
СОКпроцессором значения потребуется вы́дать на
внешние устройства; обратное преобразование
необходимо совершать при каждом вводе
информации с внешнего устройства. Подобные
преобразования
могут
быть
выполнены
программным
путём
(что
ограничивает
скорость) или с помощью специальных
аппаратных средств.

12.

Некоторые современные исследования в области
вычислений на основе СОК-арифметики
12
Операция возведения в степень в СОК для больших
чисел может быть реализована весьма
эффективно, что
приводит к сверхлинейному ускорению вычислений. (СИСТЕМА
ОСТАТОЧНЫХ КЛАССОВ. Научный блог Максима Дерябина:
http://mderyabin.ru/rns).
Модулярно-логарифмический сопроцессор для массовых
арифметических вычислений (также здесь), Илья Осинин, г.
Саро́в.
Возможности распознавания ошибок и их коррекции на основе свойств СОК (материалы статьи
КОРРЕКТИРУЮЩИЕ СВОЙСТВА КОДОВ СИСТЕМЫ ОСТАТОЧНЫХ КЛАССОВ (СОК). Петросян С.М.,
Маркарян Д.М., Калита Д.И. (http://stavkombez.ru/conf/2012/04/19/%D0%BA%D0%BE%D1%80%D1%80
%D0%B5%D0%BA%D1%82%D0%B8%D1%80%D1%83%D1%8E%D1%89%D0%B8%D0%B5-%D1%81%D0
%B2%D0%BE%D0%B9%D1%81%D1%82%D0%B2%D0%B0-%D0%BA%D0%BE%D0%B4%D0%BE%D0%B2%D1%81%D0%B8%D1%81%D1%82%D0%B5).
ПРИНЦИПЫ ПОСТРОЕНИЯ МОДУЛЯРНЫХ СУММАТОРОВ И
УМНОЖИТЕЛЕЙ. Червяков Н.И., Дьяченко И.В. (см. статью в
формате PDF на ресурсе http://www.computer-museum.ru/
books/archiv/sokcon37.pdf)
ИНФОРМАЦИОННЫЕ
ТЕХНОЛОГИИ
НА
ОСНОВЕ
МОДУЛЯРНОЙ АЛГЕБРЫ. Жуков-Емельянов О.Д. (см. ресурс
http://urss.ru/cgi-bin/
db.pl?lang=Ru&blang=ru&page=Book &id=111509)

13.

Информация для самостоятельной работы
12
Ключевые слова для поиска в сети InterNet: система счисления;
натуральная, позиционная и непозиционные системы счисле́ния; система
счисления на основе факториалов; система счисления на основе чисел
Фибоначчи; система счисления на основе остаточных классов; система
оснований; взаимно-простые числа; модулярная арифметика; о модулярной
арифметике на HABRAHABR’е; вы́чет; китайская теорема об остатках;
загадка китайского математика Сунь Цзы (III век н.э.); китайский математик
Цань Цзю-шао (XIII век н.э.); М.Валах; А.Свобода; модуля́рные ЭВМ "Эпос" и
"Эпос-2"; Израиль Акушский; Давлет Юдицкий; Юрий Базилевский; Башир
Рамеев; Юлий Шрейдер; Е.С.Андрианов; Фёдор Лукин; суперЭВМ А-340А;
суперЭВМ 5Э53 для системы ПРО А-35 (ещё); РЛС “Дунай-3УП” системы ПРО
А-35; задачи для ЭВМ с диапазоном сверхбольши́х чисел - числа Ферма,
совершенные нечётные числа, числа Мерсенна; операции по модулю в
системах криптографии (ещё, ещё, ещё… обзор).
Дополнительно: системы счисления – ссылка-1; ссылка-2; малоизвестншые
ЭВМ - 5Э53-ссылка-1; 5Э53-ссылка-2; разработки Зеленограда – ссылка-1;
ссылка-2.
…ещё больше поисковых систем
Некоторые известные (и популярные!) системы поиска информации в
Сети: (больше – здесь); о модуля́рных суперЭВМ – тут, здесь и здесь.
Баканов Валерий Михайлович
E-Mail:
WEB:
[email protected]
http://vbakanov.ru