Похожие презентации:
Подобные треугольники
1.
Здравствуйте, ребята!Запишите в тетради:
Первое февраля
Подобные треугольники.
2.
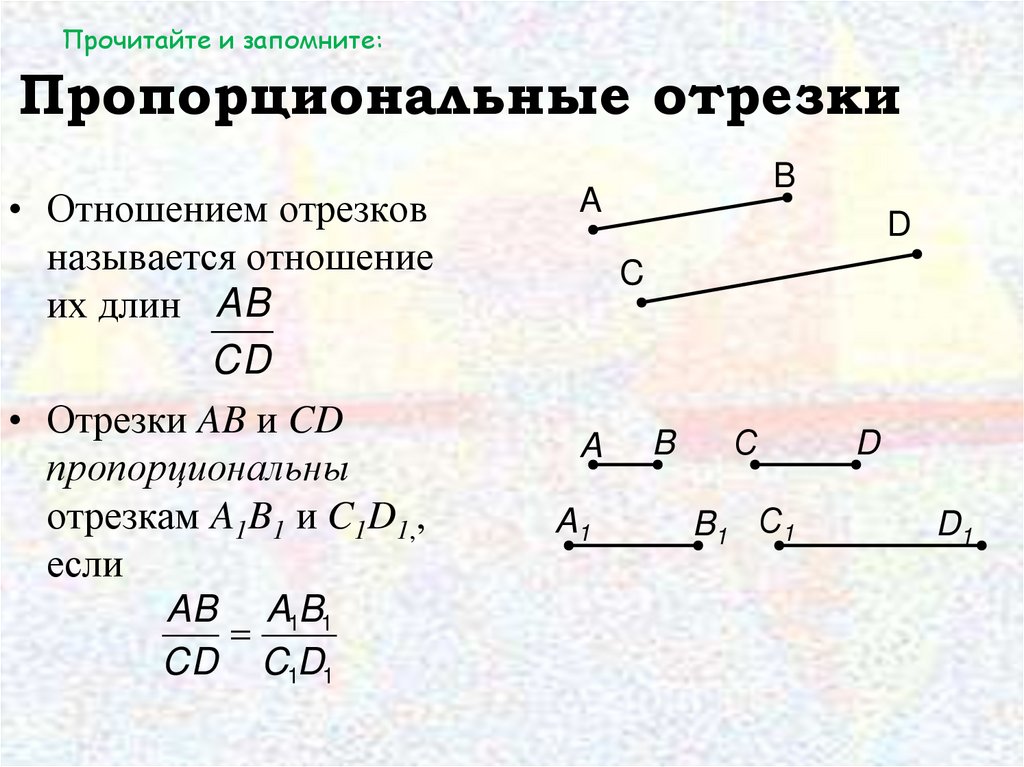
Прочитайте и запомните:Пропорциональные отрезки
• Отношением отрезков
называется отношение
их длин AB
CD
• Отрезки AB и CD
пропорциональны
отрезкам A1B1 и C1D1,,
если
AB A1B1
CD C1D1
B
A
D
C
A
A1
B
С
B1 С1
D
D1
3.
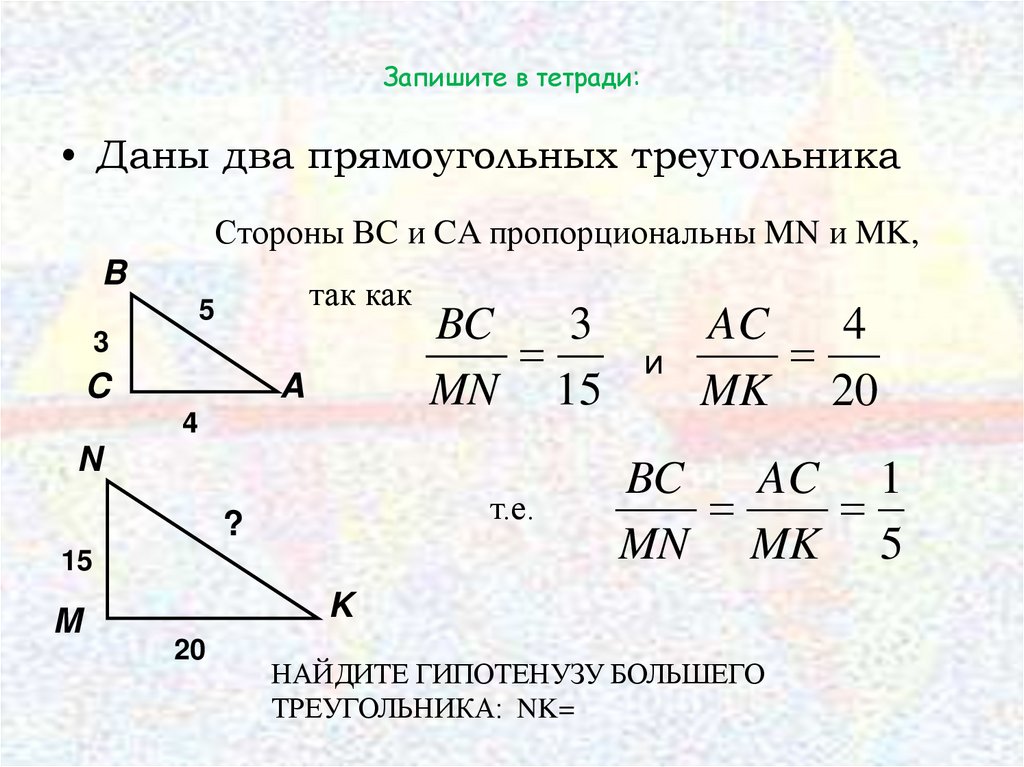
Запишите в тетради:• Даны два прямоугольных треугольника
Стороны ΒC и CA пропорциональны MN и MK,
B
так как
5
3
C
A
4
BC
3
MN 15
N
т.е.
?
15
M
и
AC
4
MK 20
BC
AC 1
MN MK 5
K
20
НАЙДИТЕ ГИПОТЕНУЗУ БОЛЬШЕГО
ТРЕУГОЛЬНИКА: NK=
4.
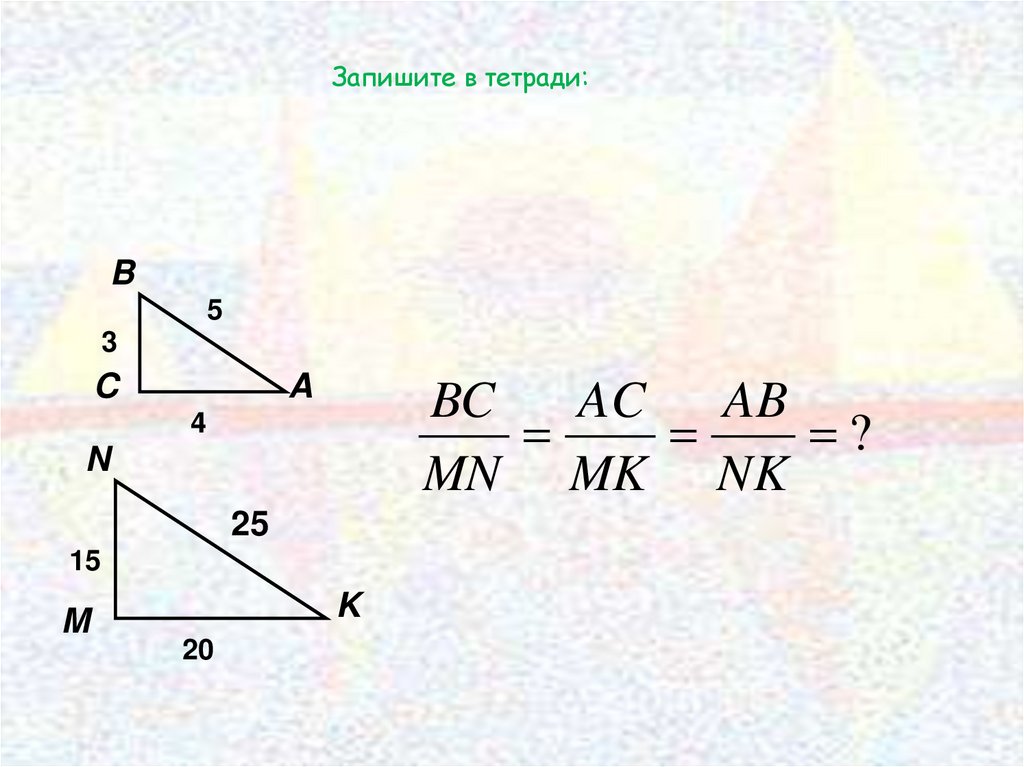
Запишите в тетради:B
5
3
C
A
BC
AC AB
?
MN MK NK
4
N
25
15
M
K
20
5.
Ознакомьтесь:Подобные фигуры
Предметы одинаковой
формы, но разных
размеров
Фотографии, отпечатанные
с одного негатива, но с
разными увеличениями;
Здание и его макет
Планы,
географические
карты одного и того
же района,
выполненные в
разных масштабах.
6.
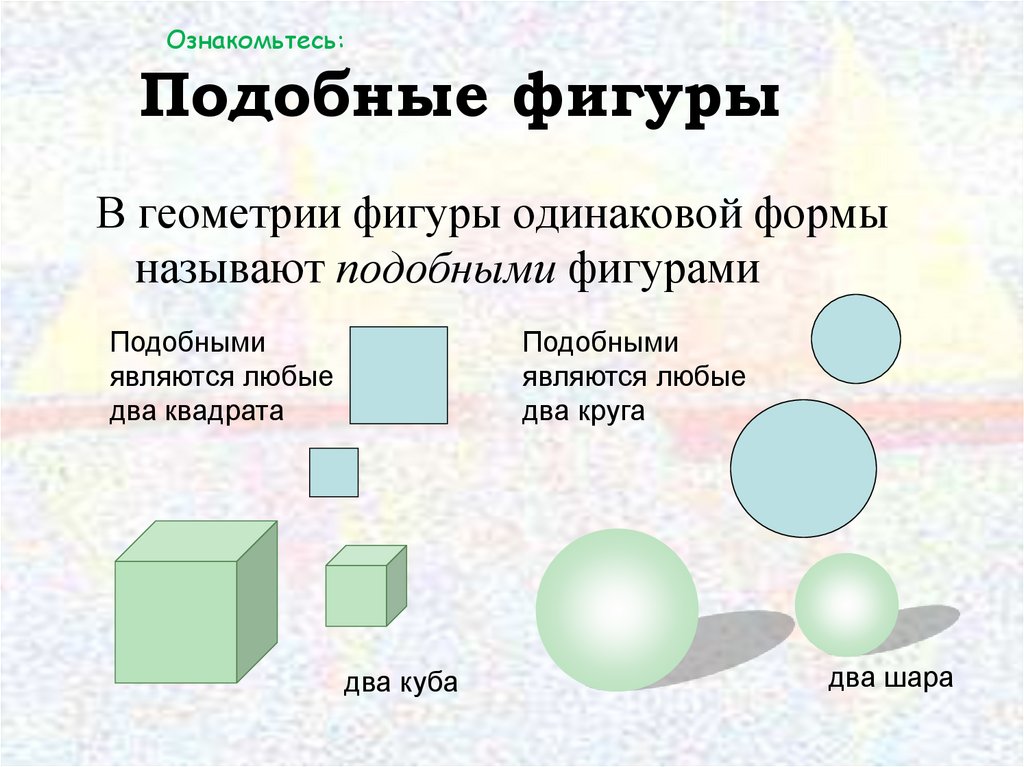
Ознакомьтесь:Подобные фигуры
В геометрии фигуры одинаковой формы
называют подобными фигурами
Подобными
являются любые
два квадрата
Подобными
являются любые
два круга
два куба
два шара
7.
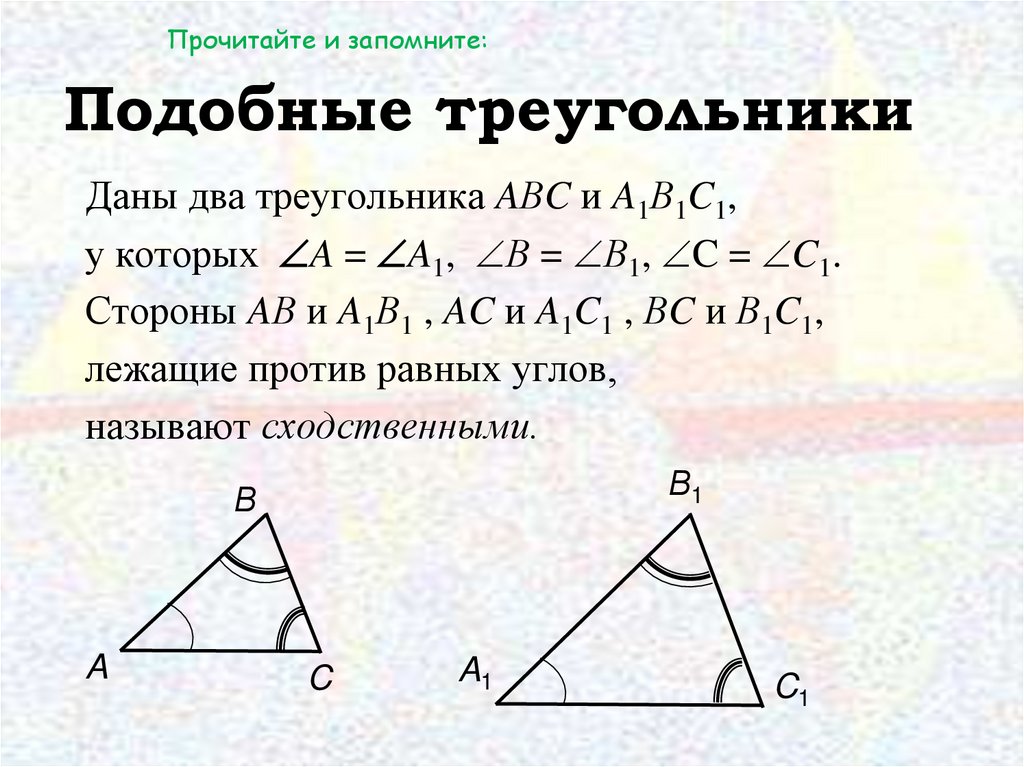
Прочитайте и запомните:Подобные треугольники
Даны два треугольника AΒC и A1Β1C1,
у которых A = A1, Β = Β1, C = C1.
Стороны AΒ и A1Β1 , AC и A1C1 , ΒC и Β1C1,
лежащие против равных углов,
называют сходственными.
Β1
Β
A
C
A1
C1
8.
Запишите:Определение
Два треугольника называются подобными,
если их углы соответственно равны и
стороны одного треугольника
пропорциональны сходственным сторонам другого.
Β
A
ΔAΒC ~ ΔA1Β1C1
C
A1
Β1
A = A1, Β = Β1, C = C1.
C1
AB
BC
AC
A1B1 B1C1 A1C1
9.
Запишите:Коэффициент подобия
Β
ΔAΒC ~ ΔA1Β1C1
AB
BC
AC
k
A1B1 B1C1 A1C1
A
Β1
C
A1
k – коэффициент подобия.
Число k , равное отношению сходственных сторон,
называется коэффициентом подобия.
C1
10.
Запишите:Дополнительные свойства
Отношение высот подобных треугольников,
проведенных к сходственным сторонам, равно
коэффициенту подобия.
Отношение медиан подобных треугольников,
проведенных к сходственным сторонам, равно
коэффициенту подобия.
Отношение биссектрис подобных треугольников,
проведенных к сходственным сторонам, равно
коэффициенту подобия.
11.
Запишите:Отношение периметров
Β
Β1
ΔAΒC ~ ΔA1Β1C1
AB
BC
AC
k
A1B1 B1C1 A1C1
A
C
A1
PABC
k
PA1B1C1
Отношение периметров подобных
треугольников равно
коэффициенту подобия.
C1
12.
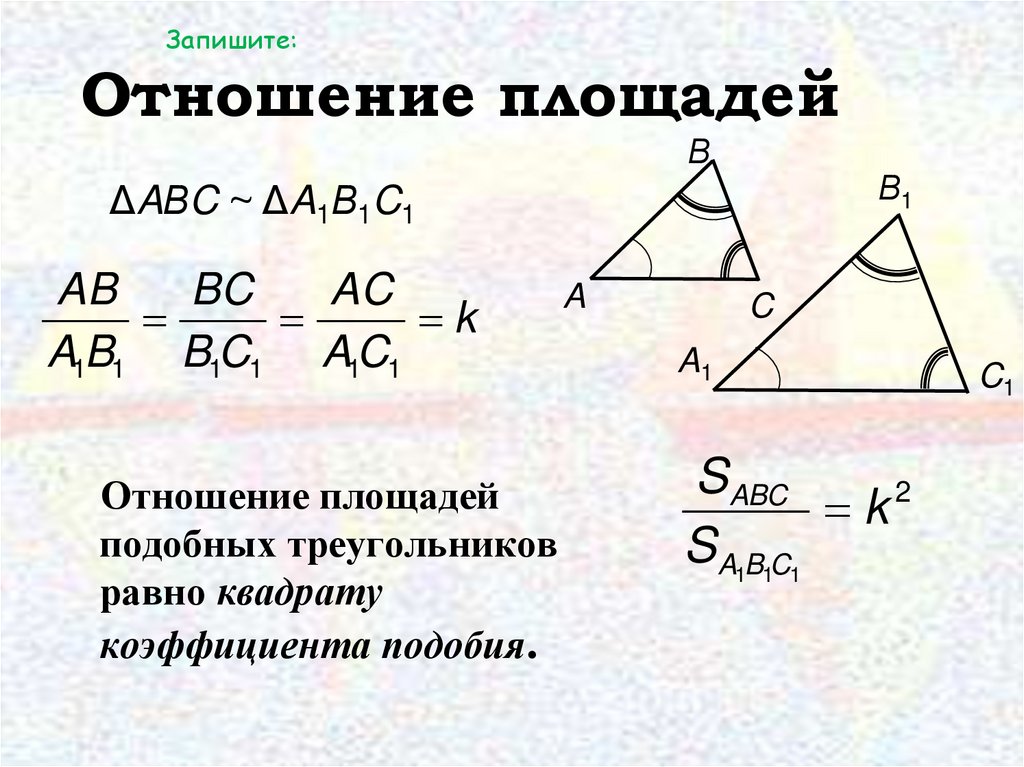
Запишите:Отношение площадей
Β
Β1
ΔAΒC ~ ΔA1Β1C1
AB
BC
AC
k
A1B1 B1C1 A1C1
Отношение площадей
подобных треугольников
равно квадрату
коэффициента подобия.
A
C
A1
S ABC
2
k
S A1B1C1
C1
13.
Задание:к следующему уроку выучите конспект, записанный у вас в тетради.
Присылать учителю ничего не нужно.







 Математика
Математика








