Подобные треугольники

1.

2.

Два треугольника называются
подобными, если
A) их углы соответственно равны.
B) стороны одного треугольника
пропорциональны сходственным
сторонам другого треугольника.
C) их углы соответственно равны и
стороны одного треугольника
пропорциональны сходственным
сторонам другого треугольника.

3.

Число, равное отношению сходственных
сторон подобных треугольников,
называется
A) угловым коэффициентом
B) коэффициентом подобия
С) коэффициентом треугольника
Отношение площадей двух подобных
треугольников равно
А) коэффициенту подобия
В) квадрату коэффициента подобия
С) невозможно определить

4.

Отношение периметров двух подобных
треугольников равно
А) коэффициенту подобия
В) квадрату коэффициента подобия
С) невозможно определить
Биссектриса треугольника делит
противоположную сторону на отрезки,…
А) равные прилежащим сторонам
треугольника
В) пропорциональные противолежащим
сторонам треугольника
С) пропорциональные прилежащим сторонам
треугольника

5.

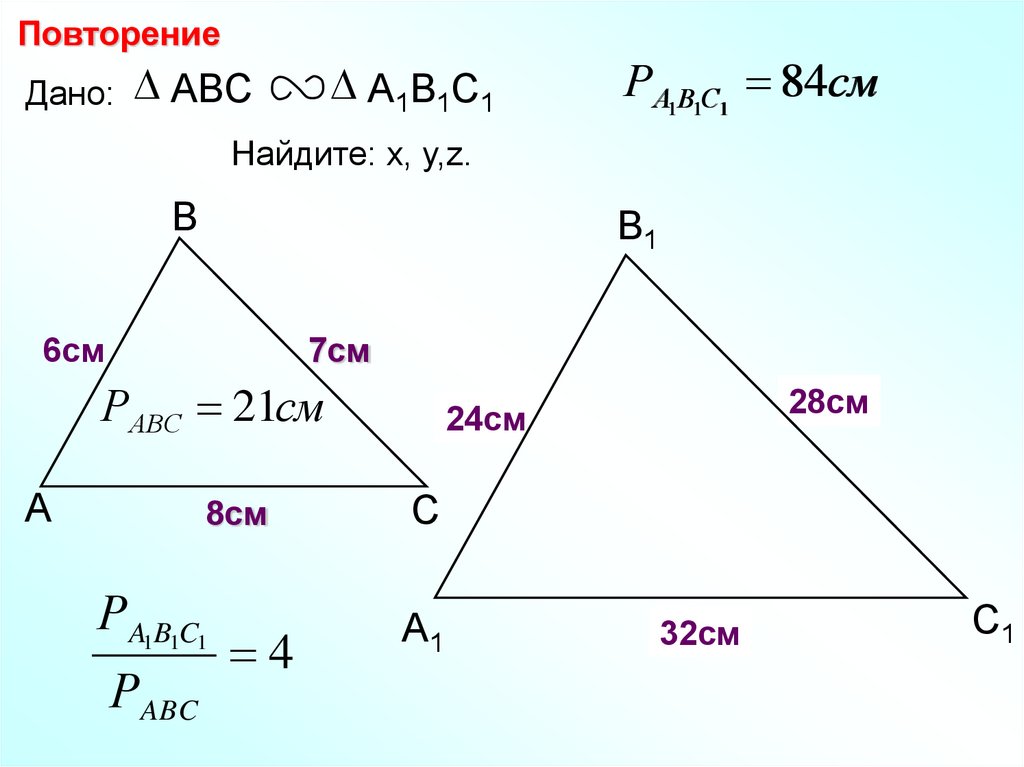
Повторение
Дано:
ABC
А1В1С1
РА1В1С1 84см
Найдите: х, у,z.
В
В1
6см
7см
РАВС 21см
А
8см
РA1B1C1
РABC
4
28см
y
х
24см
С
А1
z
32см
С1

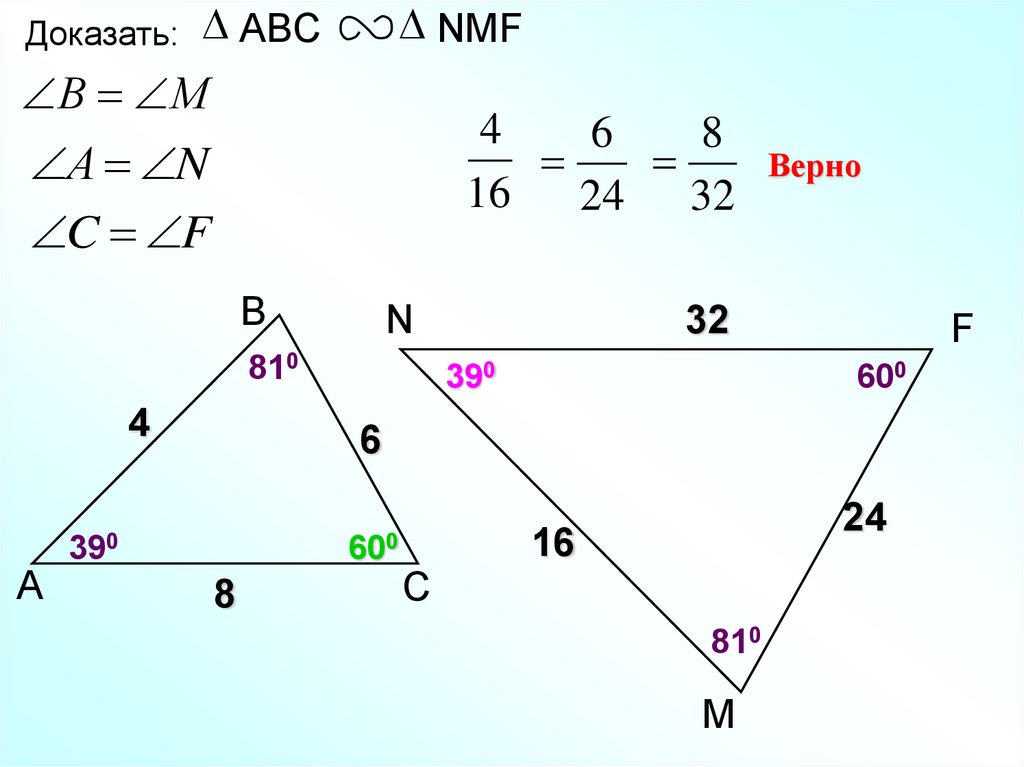
6.

Доказать:
ABC
NMF
В М
4
6
8
16
24 32
А N
C F
В
N
810
4
А
Верно
32
390
F
600
6
390
600
8
24
16
С
810
М

7.

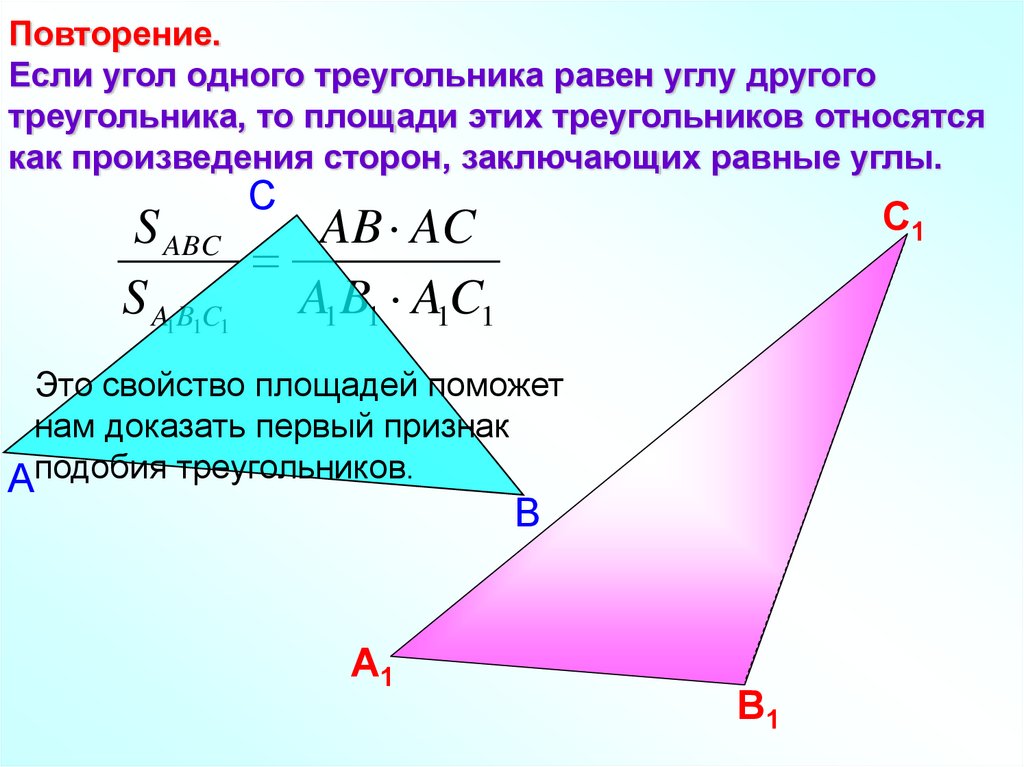
Повторение.
Если угол одного треугольника равен углу другого
треугольника, то площади этих треугольников относятся
как произведения сторон, заключающих равные углы.
С
S ABC
AB AC
S A1B1C1 A1 B1 A1C1
С1
Это свойство площадей поможет
нам доказать первый признак
Аподобия треугольников.
В
А1
В1

8.

9.

Если два угла одного треугольника соответственно
равны двум углам другого, то такие треугольники
подобны.
С
Дано: ABC, А1В1С1, А А1 , В В1 ,
Доказать:
А
В
ABC
А1В1С1
Доказательство:
С1
1). С 180 А В
0
С1 1800 А1 В1
С С1
А1
В1

10.

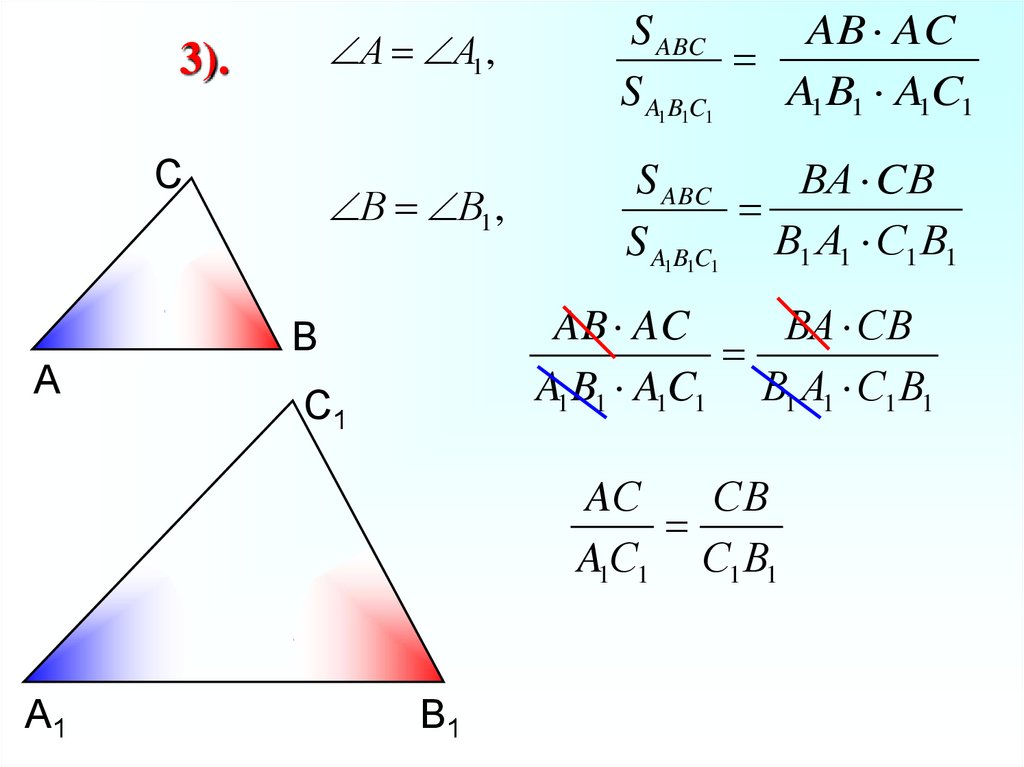
А А1 ,
2).
С
А
С С1
AB AC
S ABC
S A1B1C1 A1 B1 A1C1
СA CВ
S ABC
S A1B1C1 С1 А1 С1 В1
AB AC
СА СВ
A1 B1 A1C1 С1 А1 С1 В1
В
С1
AB
СВ
A1 B1 С1 В1
А1
В1

11.

3).
С
А
А А1 ,
AB AC
S ABC
A1 B1 A1C1
S A1B1C1
В В1 ,
ВA CВ
S ABC
S A1B1C1 В1 А1 С1 В1
AB AC
ВА СВ
A1 B1 A1C1 В1 А1 С1 В1
В
С1
AС
СВ
A1С1 С1 В1
А1
В1

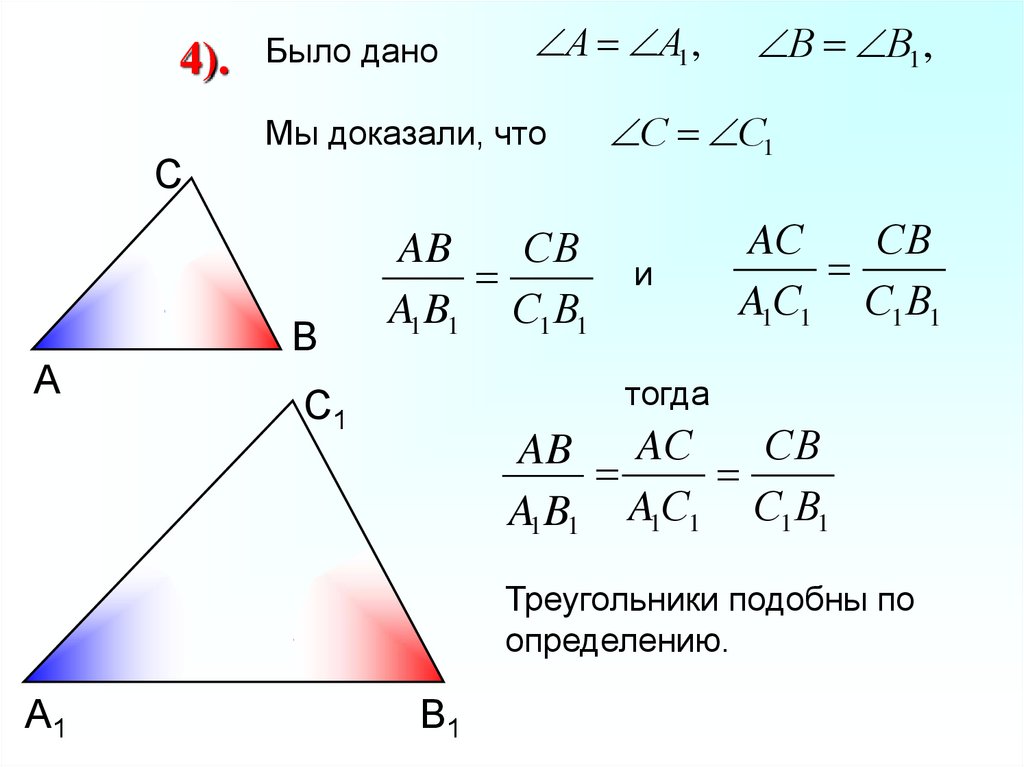
12.

4).
С
А
Было дано
А А1 ,
Мы доказали, что
В
AB
СВ
A1 B1 С1 В1
В В1 ,
С С1
и
AС
СВ
A1С1 С1 В1
тогда
С1
СВ
AB AС
A1 B1 A1С1 С1 В1
Треугольники подобны по
определению.
А1
В1

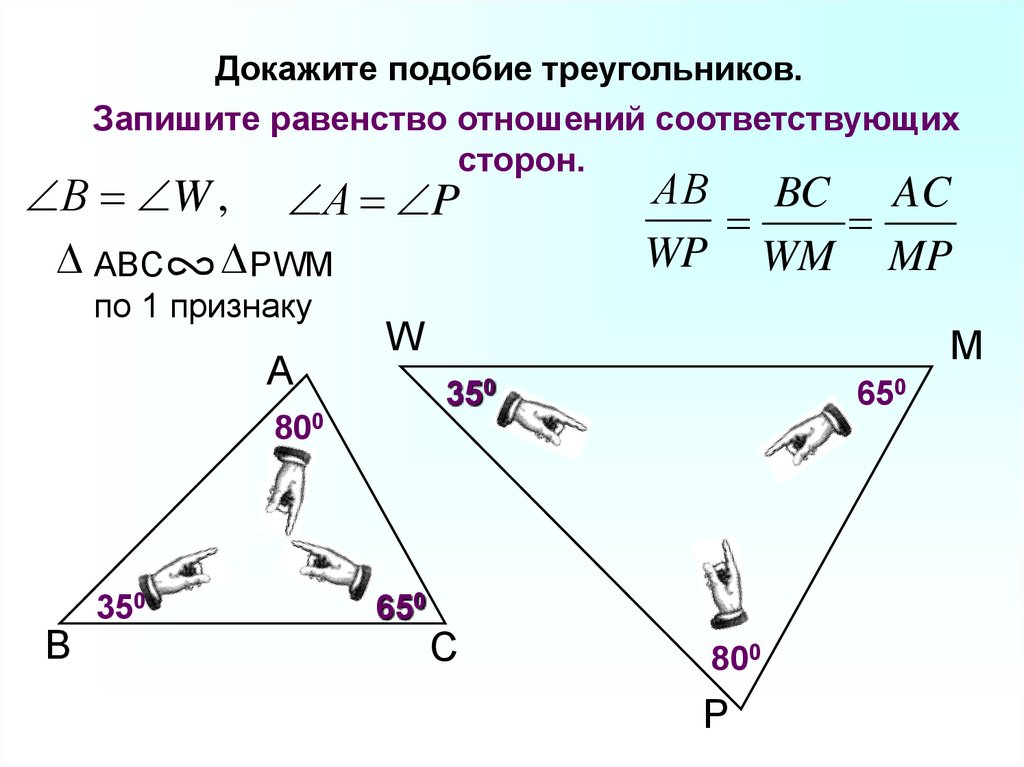
13.

Докажите подобие треугольников.
Запишите равенство отношений соответствующих
сторон.
В W , А P
ABC PWM
по 1 признаку
А
АВ BC AC
WP WM MP
W
M
350
650
800
В
350
650
С
800
P

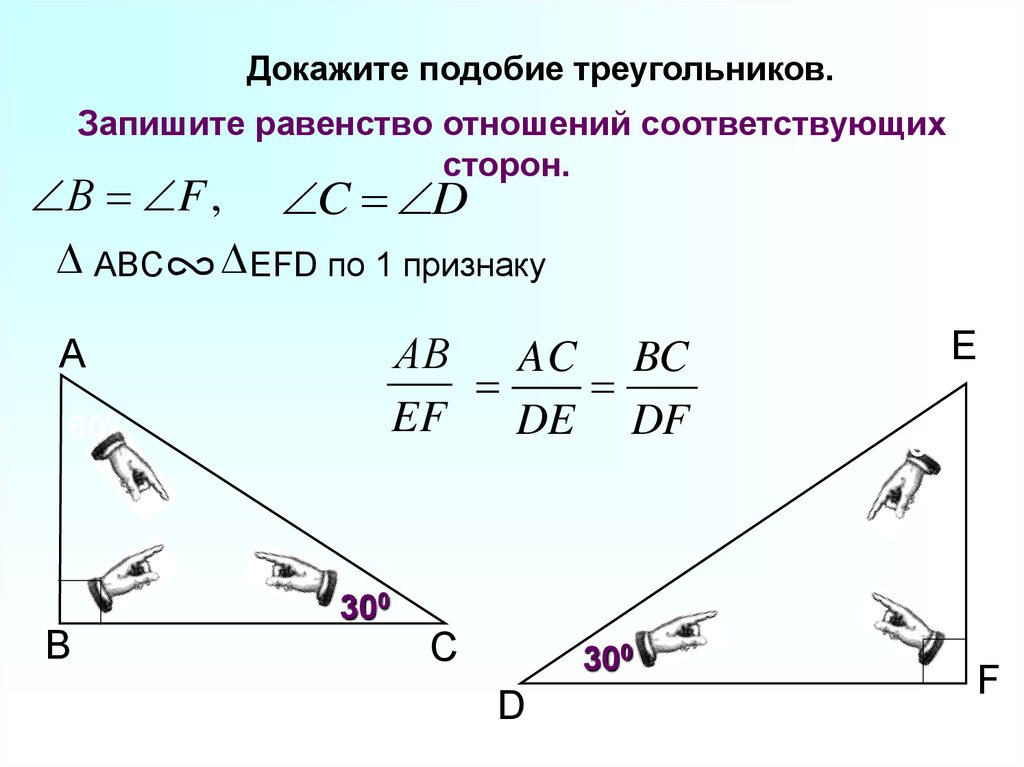
14.

Докажите подобие треугольников.
Запишите равенство отношений соответствующих
сторон.
В F , C D
ABC EFD по 1 признаку
АВ
AC BC
EF
DE DF
А
600
В
300
С
300
D
E
600
F

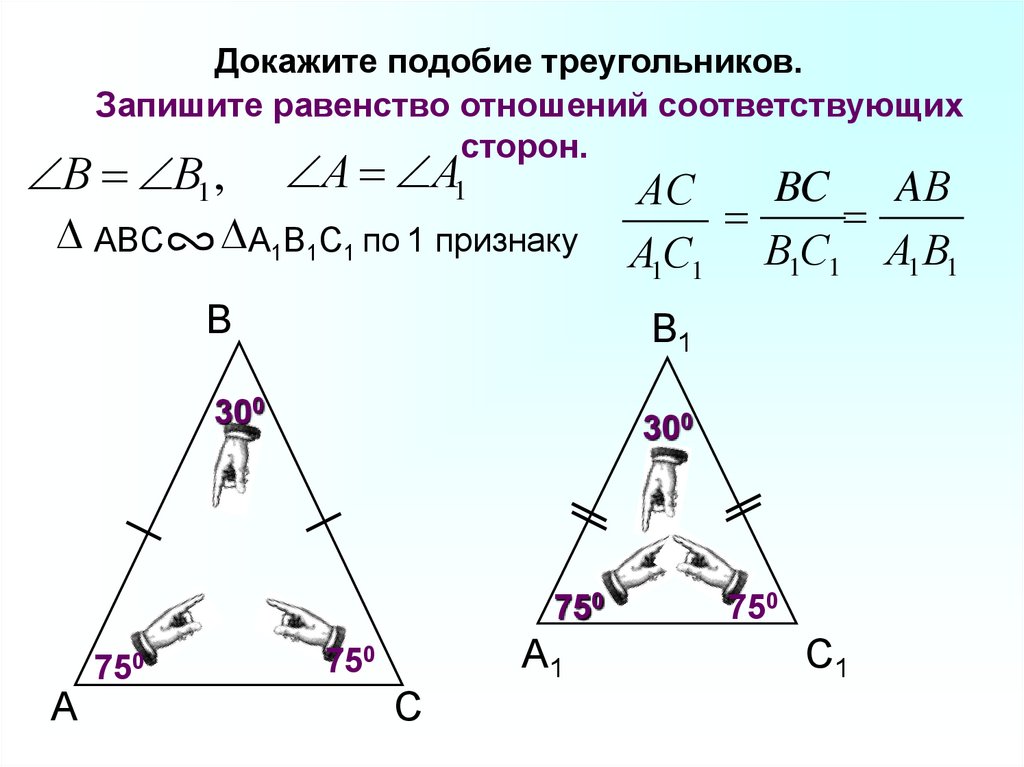
15.

Докажите подобие треугольников.
Запишите равенство отношений соответствующих
сторон.
В В1,
ABC
А А1
A1B1C1 по 1 признаку
B
B1
300
300
750
750
A
BC AВ
АС
А1С1 В1С1 А1 В1
A1
750
С
750
С1

16.

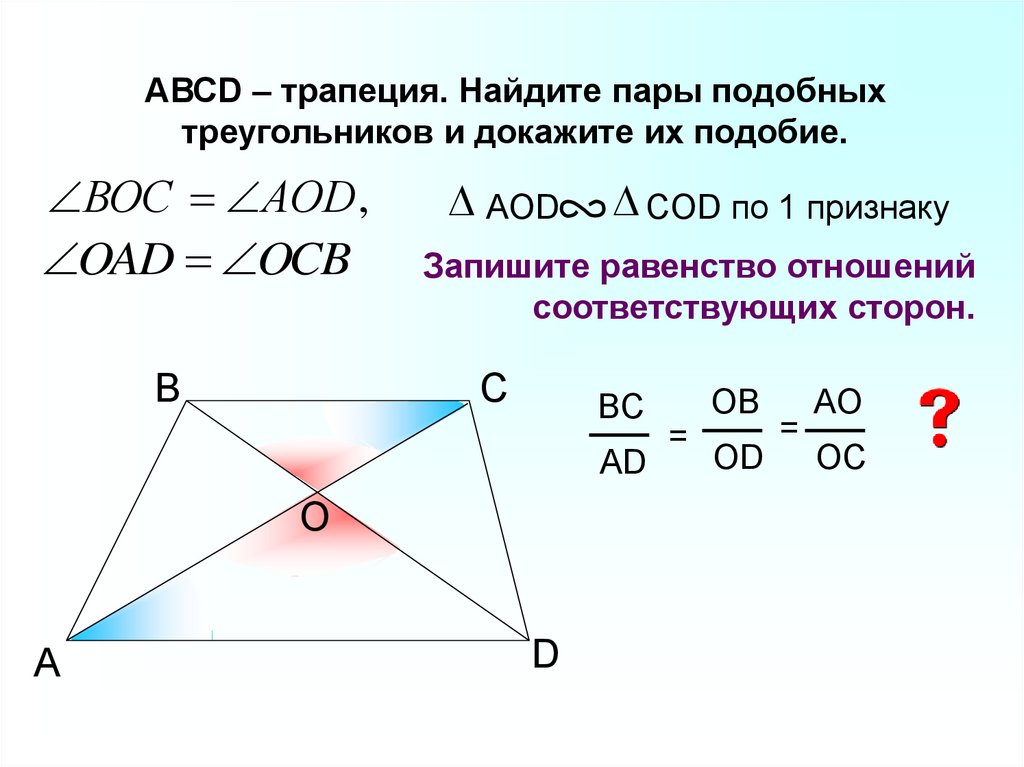
АВСD – трапеция. Найдите пары подобных
треугольников и докажите их подобие.
ВОС АОD ,
OAD OCB
AОD
Запишите равенство отношений
соответствующих сторон.
С
B
COD по 1 признаку
BC
AD
O
A
D
OB
=
OD
=
AO
OC

17.

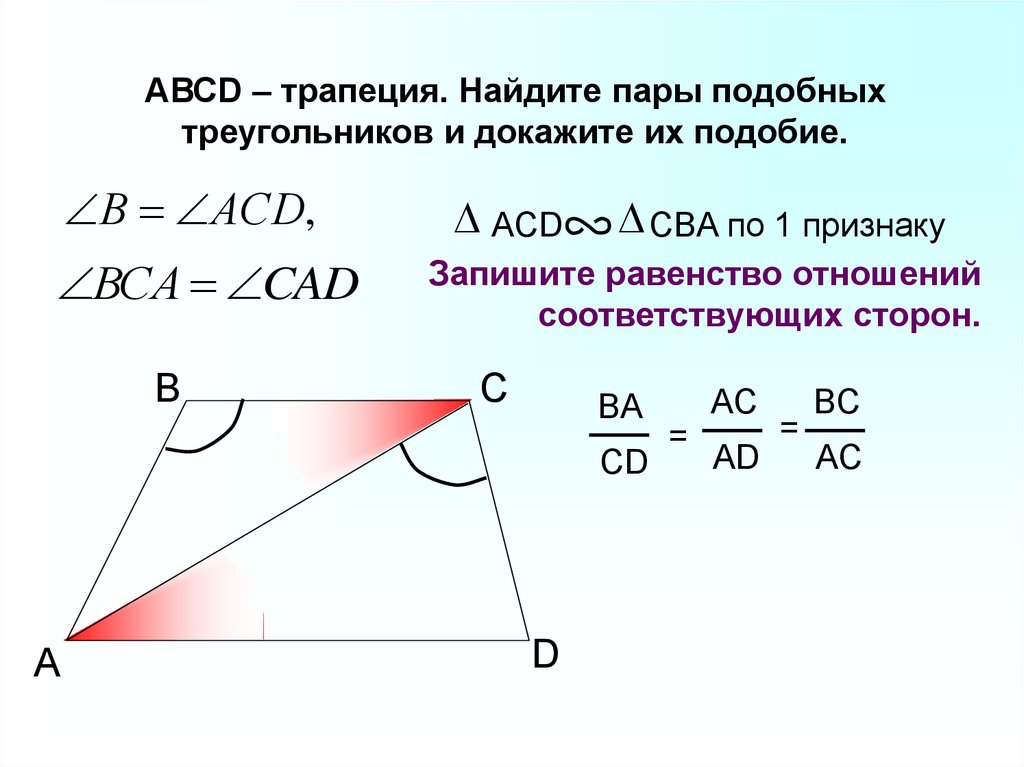
АВСD – трапеция. Найдите пары подобных
треугольников и докажите их подобие.
В АСD,
ВСА CAD
B
ACD
CBA по 1 признаку
Запишите равенство отношений
соответствующих сторон.
С
BA
CD
A
D
AC
=
AD
=
BC
AC

18.

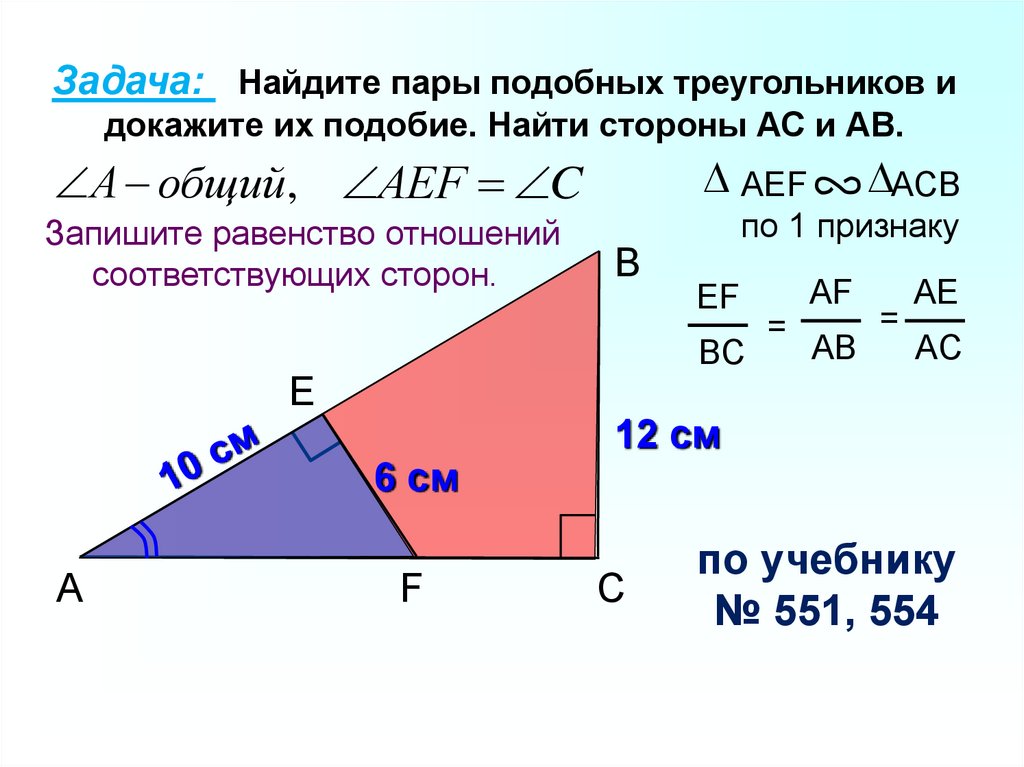
Задача: Найдите пары подобных треугольников и
докажите их подобие. Найти стороны АС и АВ.
АЕF
А общий, АЕF C
Запишите равенство отношений
соответствующих сторон.
по 1 признаку
B
EF
BC
E
6 см
A
F
ACB
AF
=
AB
=
AE
AC
12 см
C
по учебнику
№ 551, 554

19.

ТЕОРИЯ: стр. 141 – 142 –
выучить теорему с
доказательством;
ЗАДАЧИ: решить № 550, 552, 555