Похожие презентации:
How Much Information Is In A Quantum State?
1. How Much Information Is In A Quantum State?
Scott AaronsonMIT
2.
Computer Scientist / PhysicistNonaggression Pact
You accept that, for this talk:
• Polynomial vs. exponential is the basic dichotomy
of the universe
• “For all x” means “for all x”
In return, I will not inflict the following
computational complexity classes on you:
#P AM AWPP BQP BQP/qpoly MA NP P/poly PH
PostBQP PP PSPACE QCMA QIP QMA SZK YQP
3.
So, how much information is in a quantum state?An infinite amount, of course, if you want to specify
the state exactly…
1
0
0
C 2
Life is too short for infinite precision
4.
A More Serious PointIn general, a state of n possibly-entangled qubits takes
~2n bits to specify, even approximately
x x
x 0,1
Spin-½ particles
n
To a computer scientist, this is arguably the
central fact about quantum mechanics
But why should we worry about it?
5.
Answer 1: QuantumState Tomography
Task: Given lots of copies of an unknown quantum state ,
produce an approximate classical description of
Not something I just made up!
“As seen in Science & Nature”
Well-known problem: To do tomography on an entangled
state of n spins, you need ~cn measurements
Current record: 8 spins / ~656,000 experiments (!)
This is a conceptual problem—not just a practical one!
6.
Answer 2: Quantum Computing SkepticismLevin
Goldreich
‘t Hooft
Davies
Wolfram
Some physicists and computer scientists believe quantum
computers will be impossible for a fundamental reason
For many of them, the problem is that a quantum computer
would “manipulate an exponential amount of information”
using only polynomial resources
But is it really an exponential amount?
7.
Today we’ll tame the exponential beastIdea: “Shrink quantum states down to reasonable
size” by viewing them operationally
Analogy: A probability distribution over n-bit strings also takes
~2n bits to specify. But that fact seems to be “more about the
map than the territory”
• Setting the stage: Holevo’s Theorem and random access codes
• Describing a state by postselected measurements [A. 2004]
• “Pretty good tomography” using far fewer measurements [A. 2006]
- Numerical simulation [A.-Dechter, in progress]
• Encoding quantum states as ground states of simple Hamiltonians
[A.-Drucker 2009]
8.
AliceBob
Theorem [Holevo 1973]: By sending an n-qubit state
, Alice can communicate no more than n classical
bits to Bob (or 2n bits assuming prior entanglement)
How can that be? Well, Bob has to measure , and
measuring makes most of the wavefunction go poof…
Lesson: “The linearity of QM helps
tame the exponentiality of QM”
9. The Absent-Minded Advisor Problem
Can you give your graduate student a quantum statewith n qubits (or 10n, or n3, …)—such that by measuring
in a suitable basis, the student can learn your answer
to any one yes-or-no question of size n?
NO [Ambainis, Nayak, Ta-Shma, Vazirani 1999]
Indeed, quantum communication is no better than
classical for this problem as n
10.
On the Bright Side…Suppose Alice wants to describe an n-qubit state to
Bob, well enough that for any 2-outcome measurement
E, Bob can estimate Tr(E )
Then she’ll need to send ~cn bits, in the worst case.
But… suppose Bob only needs to be able to estimate
Tr(E ) for every measurement E in a finite set S.
Theorem (A. 2004): In that case, it suffices for
Alice to send ~n log n log|S| bits
11.
ALL MEASUREMENTSPERFORMABLE
ALL MEASUREMENTS
USING ≤n2 QUANTUM GATES
12.
How does the theorem work?I 321
Alice is trying to describe the quantum state to Bob
In the beginning, Bob knows nothing about , so he guesses it’s
the maximally mixed state 0=I
Then Alice helps Bob improve his guess, by repeatedly telling
him a measurement Et S on which his guess t-1 badly fails
Bob lets t be the state obtained by starting from t-1, then
performing Et and postselecting on the right outcome
13.
Claim: After only O(n) of these learning steps, Bob gets astate T such that Tr(E T) Tr(E ) for all measurements E S.
Proof Sketch: For simplicity, assume =| | is pure and
Tr(E ) is ≤1/n2 or 1-1/n2 for all E S.
Let p be the probability that E1,E2,…,ET all yield the desired
outcomes. By assumption, p is at most (say) (2/3)T
On the other hand, if Bob had made the lucky guess
0=| |, then p would’ve been at least (say) 0.9
But we can decompose I as an equal mixture of | and 2n-1
other states orthogonal to | ! Hence p 0.9/2n
0.9/2n ≤ (2/3)T T=O(n)
Conclusion: Alice can describe to Bob by telling him its
behavior on E1,E2,…,ET. This takes O(n log|S|) bits
14.
DiscussionWe’ve shown that for any n-qubit state and set S of
observables, one can “compress” the measurement data
{Tr(E )} E S into a classical string x of only Õ(nlog|S|) bits
Just two tiny problems…
1.Computing x seems astronomically hard
2.Given x, estimating Tr(E ) also seems astronomically hard
I’ll now state the “Quantum Occam’s Razor Theorem,”
which at least addresses the first problem…
15.
Quantum Occam’s RazorTheorem
Let be an unknown quantum state of n spins
Suppose you just want to be able to estimate Tr(E ) for most
measurements E drawn from some probability measure D
Then it suffices to do the following, for some m=O(n):
1. Choose E1,…,Em independently from D
2. Go into your lab and estimate Tr(Ei ) for each 1≤i≤m
3. Find any “hypothesis state” such that Tr(Ei ) Tr(Ei )
for all 1≤i≤m
16.
Theorem [A. 2006]: ProvidedC n
1
2 1
m 4 4 log
log (C a constant)
and
Tr Ei Tr Ei
2
7
states are
for all i, you’ll “Quantum
be guaranteed that
PAC-learnable”
Pr Tr E Tr E 1 ,
E~D
with probability at least 1- over the choice of E1,…,Em.
Proof combines Ambainis et al.’s result on the impossibility
of quantum compression with some power tools from
classical computational learning theory
17.
Remark 1: To do this “pretty good tomography,” you don’tneed any prior assumptions about ! (No Bayesian nuthin’...)
Removes a lot of conceptual problems...
Instead, you assume a distribution D over measurements
Might be preferable—after all, you can control which
measurements to apply, but not what is
Remark 2: Given the measurement data Tr(E1 ),…,Tr(Em ),
finding a hypothesis state consistent with it could still be
an exponentially hard computational problem
Semidefinite / convex programming in 2n dimensions
But this seems unavoidable: even finding a classical
hypothesis consistent with data is conjectured to be hard!
18.
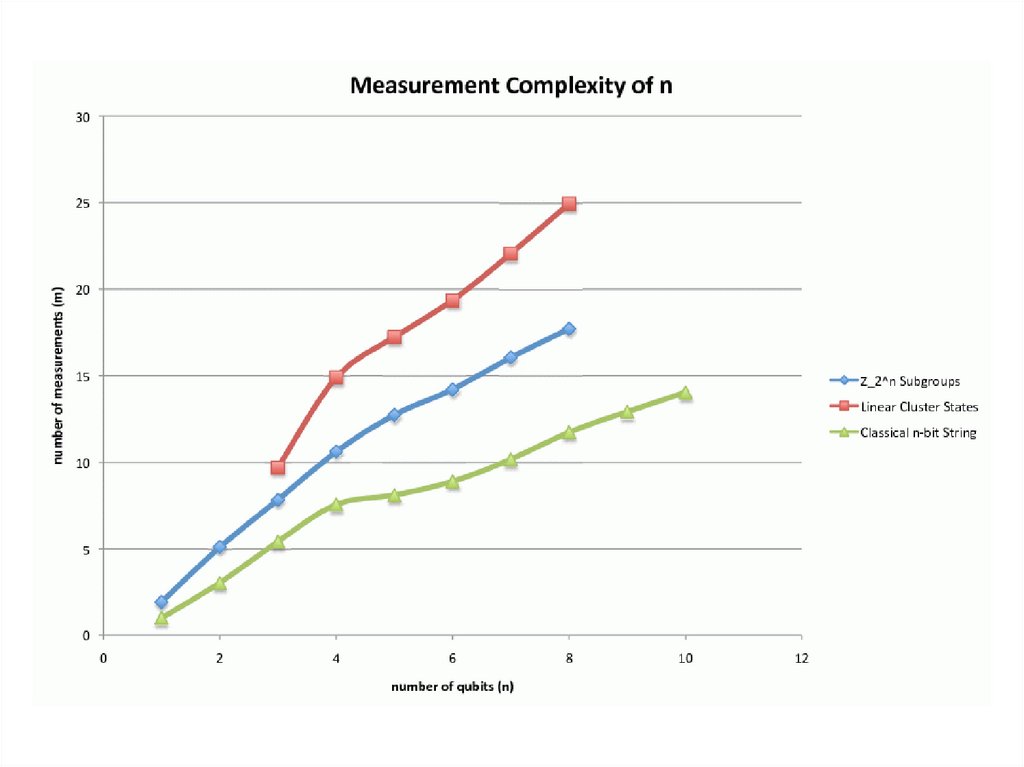
Numerical Simulation[A.-Dechter, in progress]
We implemented the “pretty-good tomography” algorithm
in MATLAB, using a fast convex programming method
developed specifically for this application [Hazan 2008]
We then tested it (on simulated data) using MIT’s
computing cluster
We studied how the number of sample measurements m
needed for accurate predictions scales with the number of
qubits n, for n≤10
Result of experiment: My theorem appears to be true
19.
20.
Recap: Given an unknown n-qubit entangled quantum state ,and a set S of two-outcome measurements…
Learning theorem: “Any hypothesis state consistent with a
small number of sample points behaves like on most
measurements in S”
Postselection theorem: “A particular state T (produced by
postselection) behaves like on all measurements in S”
Dream theorem: “Any state that passes a small number of
tests behaves like on all measurements in S”
[A.-Drucker 2009]: The dream theorem holds
Caveat: will have more qubits than , and in general be a very different state
Proof combines Quantum Occam’s Razor Theorem with a new
classical result about “isolatability” of functions
21.
A “Practical” ImplicationIt’s the year 2500. Everyone and her grandfather has a
personal quantum computer.
You’re a software vendor who sells “magic initial states”
that extend quantum computers’ problem-solving abilities.
Amazingly, you only need one kind of state in your store:
ground states of 1D nearest-neighbor Hamiltonians!
UNIVERSAL RESOURCE STATE
Reason: Finding ground states of 1D spin systems is known to
be “universal” for quantum constraint satisfaction problems
[Aharonov-Gottesman-Irani-Kempe 2007], building on [Kitaev 1999]
22.
SummaryIn many natural scenarios, the “exponentiality” of quantum
states is an illusion
That is, there’s a short (though possibly cryptic) classical
string that specifies how a quantum state behaves, on any
measurement you could actually perform
Applications: Pretty-good quantum state tomography,
characterization of quantum computers with “magic initial
states”…
Biggest open problem: Find special classes of quantum
states that can be learned in a computationally efficient way
“Experimental demonstration” would be nice too
23.
www.scottaaronson.com(/papers /talks /blog)
Postselection theorem: quant-ph/0402095
Learning theorem: quant-ph/0608142
Ground state theorem, numerical simulations: “in
preparation”






















 Физика
Физика








