Похожие презентации:
Nanophotonics class 4. Density of states
1.
NanophotonicsClass 4
Density of states
2. Outline
Spontaneous emission: an exited atom/molecule/.. decays tothe ground state and emits a photon
• Emission rates are set by Fermi’s Golden Rule
• Fermi’s Golden Rule & the number of available photon states (LDOS)
• Experiments demonstrating emission rate control via LDOS
• Conclusion
3. Fermi’s Golden Rule
• Consider an atom, molecule or quantum dot with eigenstates y.• Suppose the system is perturbed, e.g. by incident light.
Perturbing term in hamiltonian:
V μ E
light
Dipole operator
The coupling can take the atom in initial state yi to another state yf
Fermi’s Golden Rule: rate of decay of the initial state yi
2
2
all final
states f
2
y f V y i ( E f Ei )
4. Understanding Fermi’s Golden Rule
22
all final
states f
2
y f V y i ( E f Ei )
Matrix elements:
Transition strength
Selection rules
Energy conservation
Spontaneous emission of a two-level atom:
Initial state: excited atom + 0 photons.
Final state: ground state atom + 1 photon in some photon state
Question: how many states are there for the photon ???
(constraint: photon energy = atomic energy level difference)
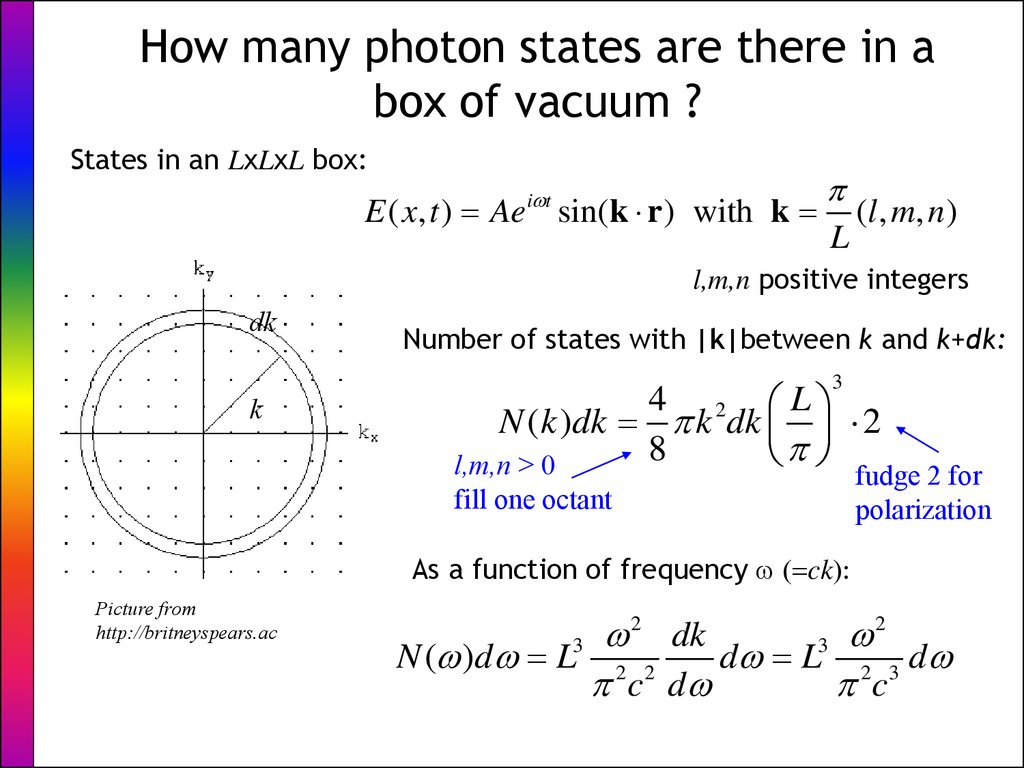
5. How many photon states are there in a box of vacuum ?
States in an LxLxL box:E ( x, t ) Aei t sin( k r ) with k
L
(l , m, n)
l,m,n positive integers
dk
k
Number of states with |k|between k and k+dk:
3
4 2 L
N (k )dk k dk 2
8
l,m,n > 0
fill one octant
fudge 2 for
polarization
As a function of frequency ( ck):
Picture from
http://britneyspears.ac
2
2
dk
N ( )d L3 2 2
d L3 2 3 d
c d
c
6. Density of states in vacuum
22 dk
3
N ( )d L 2 2
d L 2 3 d
c d
c
3
-1
Density of photon states per unit volume (s )
Example: ~50000 photon states per m3 of vacuum per 1 Hz @ l=500 nm
150000
100000
~ 50000 states
50000
l nm
0
0
2
4
15
6
-1
Frequency (10 s )
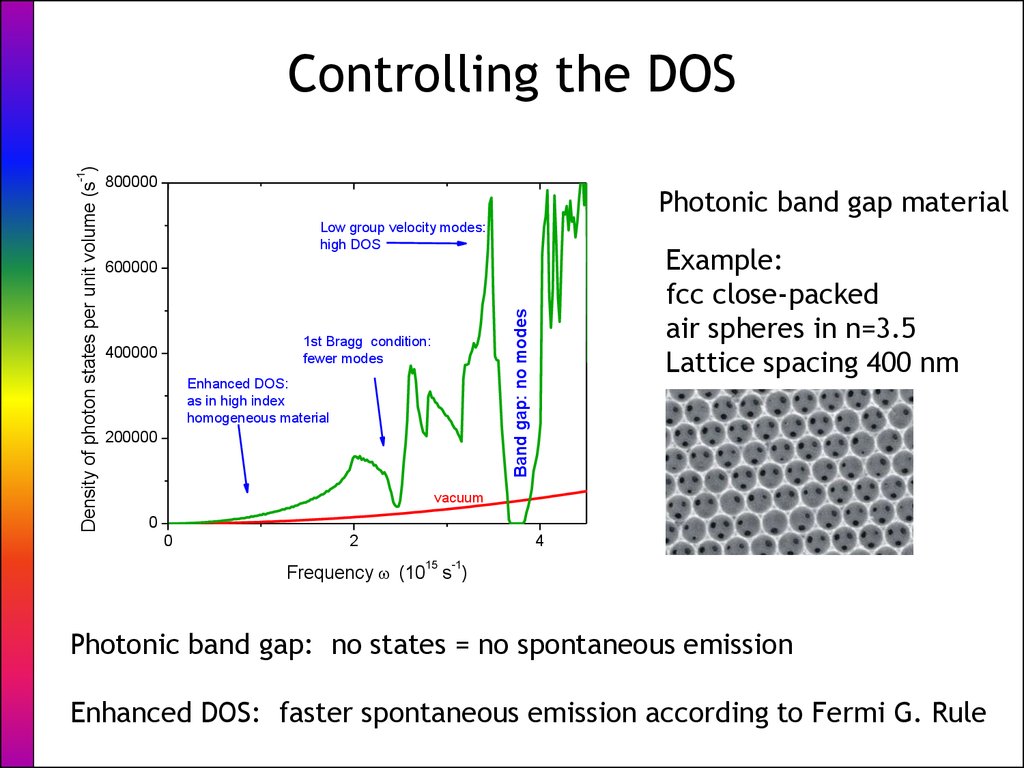
7. Controlling the DOS
800000Photonic band gap material
Low group velocity modes:
high DOS
Example:
fcc close-packed
air spheres in n=3.5
Lattice spacing 400 nm
600000
Band gap: no modes
-1
Density of photon states per unit volume (s )
Controlling the DOS
1st Bragg condition:
fewer modes
400000
Enhanced DOS:
as in high index
homogeneous material
200000
vacuum
0
0
2
4
15
-1
Frequency (10 s )
1 m
Photonic band gap: no states = no spontaneous emission
Enhanced DOS: faster spontaneous emission according to Fermi G. Rule
8. Local DOS
An emitter doesn’t just count modes (as in DOS)It also feels local mode strength |E|2.
It can only emit into a mode if the mode is not zero at the emitter
DOS: just count states
N ( )
Local DOS
N (r, d, )
( m )
all modes m
| d Em (r) |2 ( m )
all modes
Atom at position A can not emit into
cavity mode.
A
B
Atom at position B can emit into
cavity mode.
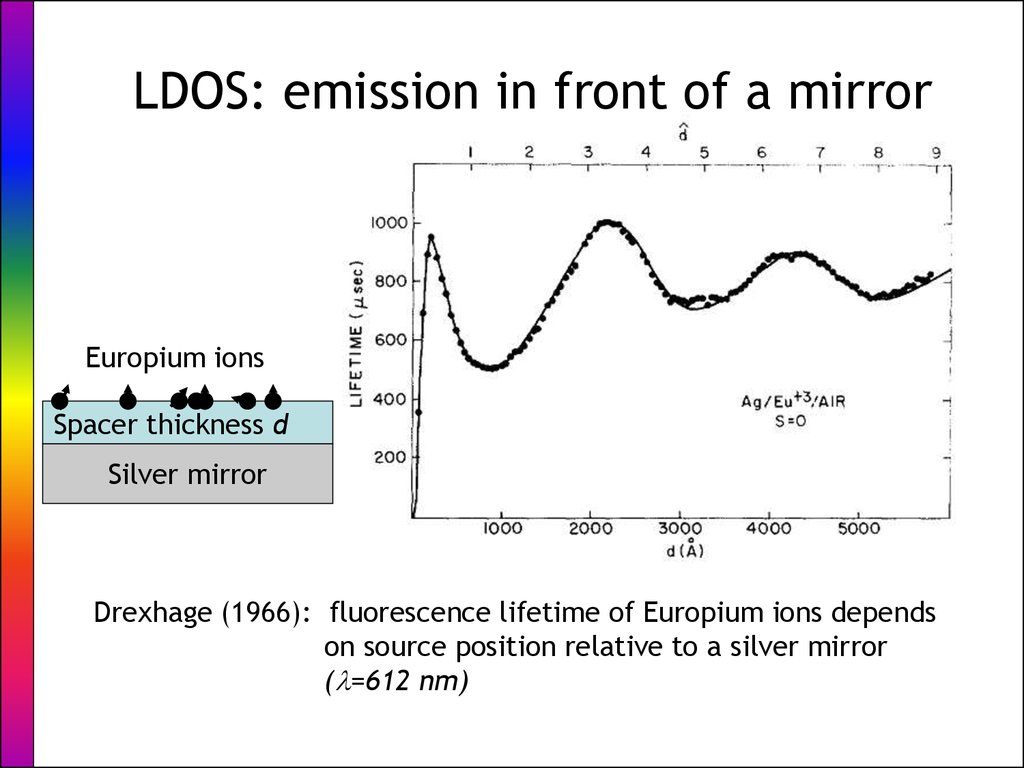
9. LDOS: emission in front of a mirror
Europium ionsSpacer thickness d
Silver mirror
Drexhage (1966): fluorescence lifetime of Europium ions depends
on source position relative to a silver mirror
(l=612 nm)
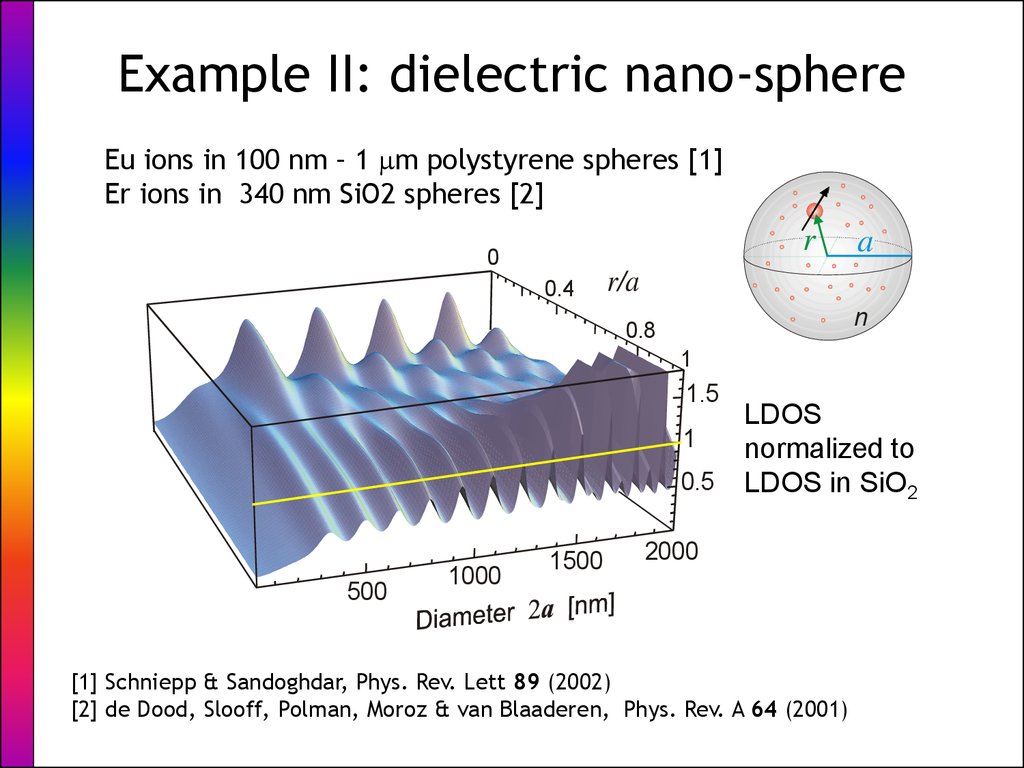
10. Example II: dielectric nano-sphere
Eu ions in 100 nm – 1 m polystyrene spheres [1]Er ions in 340 nm SiO2 spheres [2]
r
0
0.4
a
r/a
n
0.8
1
1.5
1
0.5
500
1000
1500
RLDOS
normalized to
Rbulk
LDOS in SiO2
2000
[1] Schniepp & Sandoghdar, Phys. Rev. Lett 89 (2002)
[2] de Dood, Slooff, Polman, Moroz & van Blaaderen, Phys. Rev. A 64 (2001)
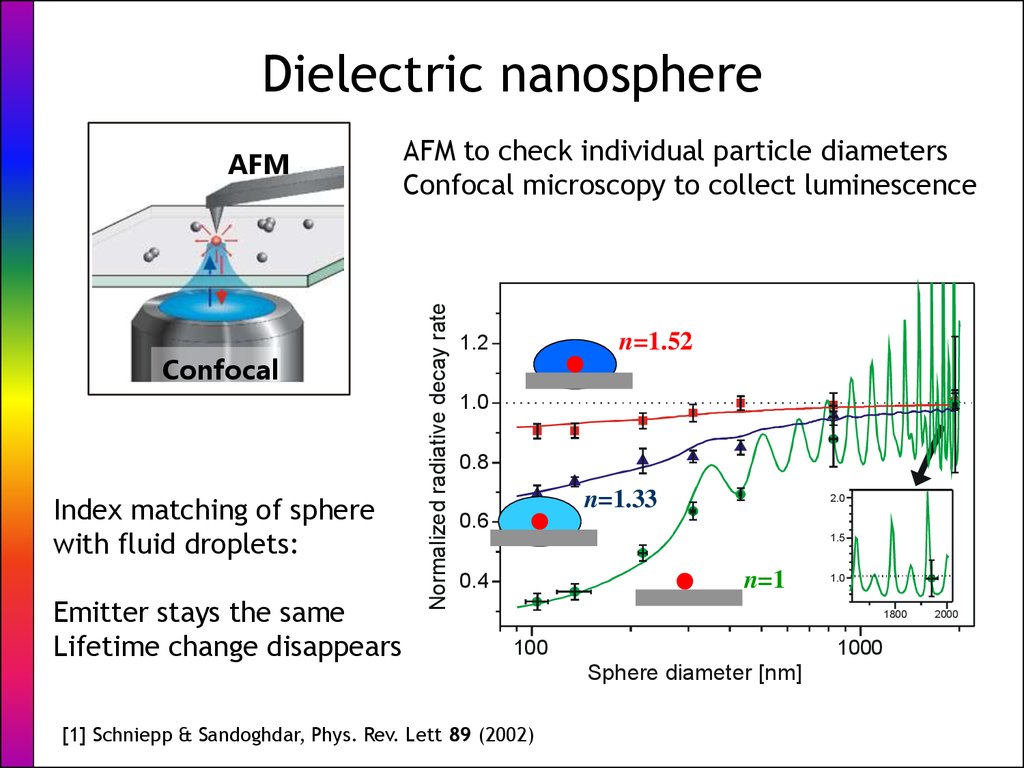
11. Dielectric nanosphere
AFMConfocal
Index matching of sphere
with fluid droplets:
Emitter stays the same
Lifetime change disappears
AFM to check individual particle diameters
Confocal microscopy to collect luminescence
Normalized radiative decay rate
b)
n=1.52
1.2
1.0
0.8
n=1.33
2.0
0.6
1.5
n=1
0.4
1.0
1800
100
1000
Sphere diameter [nm]
[1] Schniepp & Sandoghdar, Phys. Rev. Lett 89 (2002)
2000
12. LDOS & measuring nonradiative decay
LDOS & measuring nonradiative decayA real emitter often also decays nonradiatively (no photons but heat)
total non radiative radiative
Measured in experiment
Unknown loss
local chemistry
at source
Fermi’s Golden Rule
LDOS
Measurement technique: vary the nanophotonic configuration
vary LDOS and not the chemistry
Example
Emitter in sphere: index match sphere to vary
Assignment: you can find
non radiative
radiative
by varying LDOS
13. Conclusions
• Spontaneous emission rates are controlled by nanophotonic structures• Fermi’s Golden Rule: transition rate depends on availability
of final states
• Spontaneous emission: final states for photon ?
• Density of states (DOS): number of photon states depending on frequency
• Local density of states (LDOS): number of photon states available
locally for spontaneous emission
Applications
• Enhance the efficiency of light sources
• Characterize non-radiative mechanisms








 Физика
Физика








