Похожие презентации:
Компьютерная графика
1. Компьютерная графика
2. 1. Введение
Вобработке
изображениями,
направления:
информации,
связанной
с
выделяют
три
основных
• Распознавание образов
• Обработка изображений
• Машинная (компьютерная) графика
3. Распознавание образов
• Распознавание образов (изображений) естьсовокупность
методов,
позволяющих
получить
описание
изображения,
поданного на вход, либо отнести заданное
изображение к некоторому классу
4.
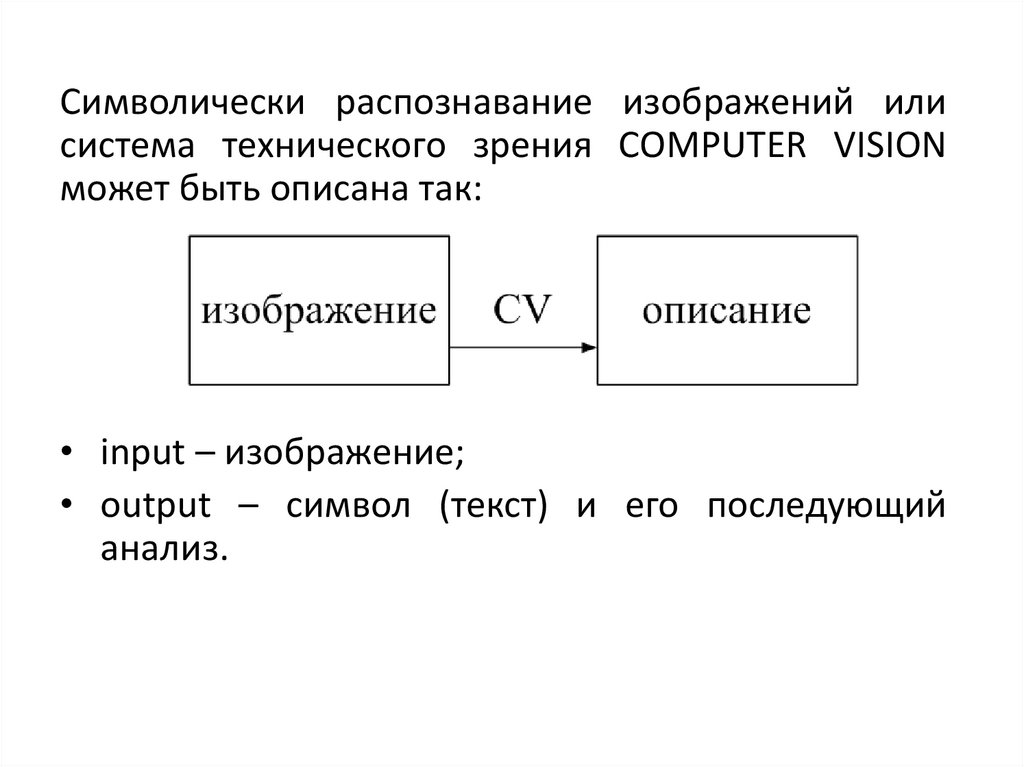
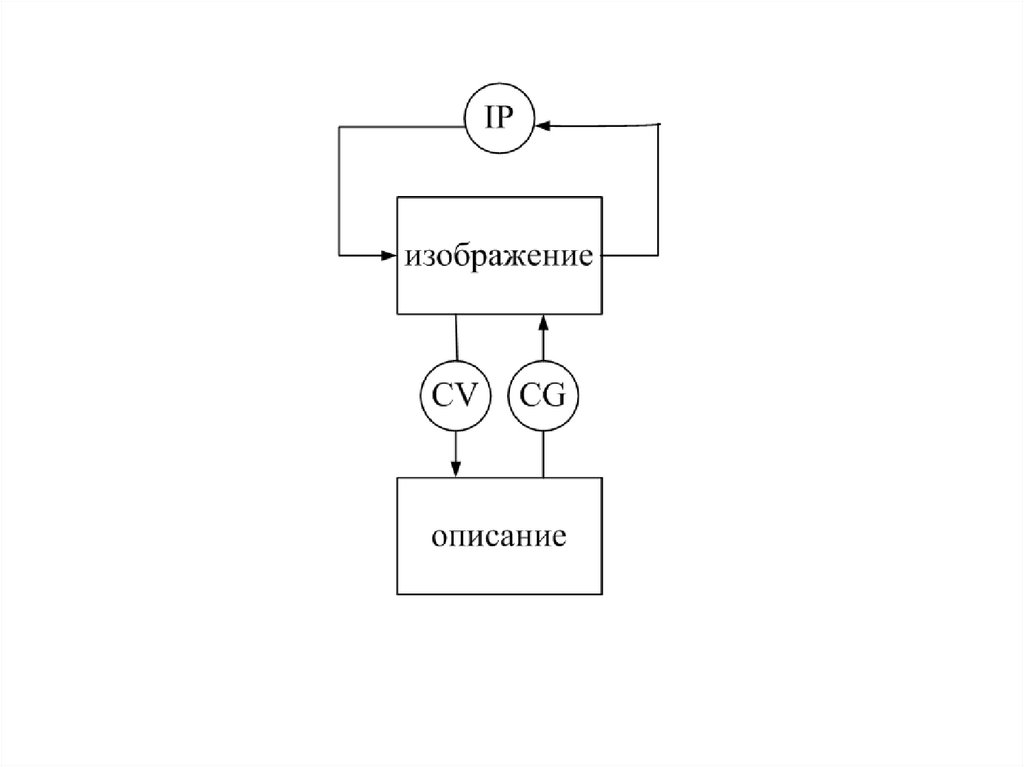
Символически распознавание изображений илисистема технического зрения COMPUTER VISION
может быть описана так:
• input – изображение;
• output – символ (текст) и его последующий
анализ.
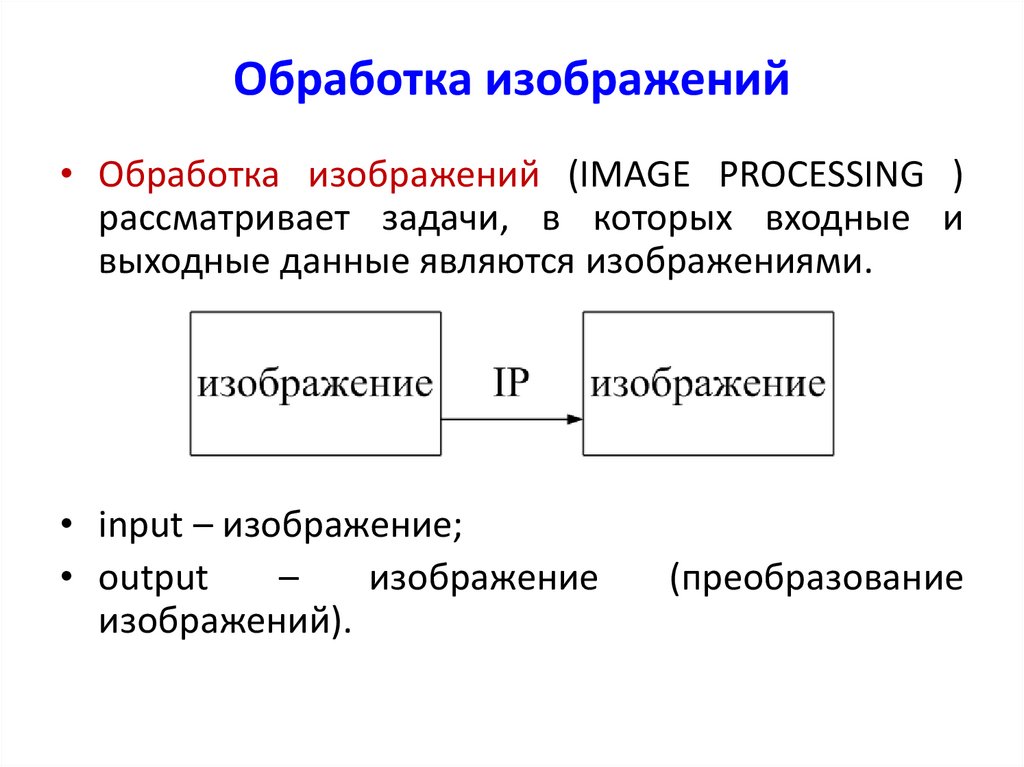
5. Обработка изображений
• Обработка изображений (IMAGE PROCESSING )рассматривает задачи, в которых входные и
выходные данные являются изображениями.
• input – изображение;
• output
–
изображение
изображений).
(преобразование
6. Компьютерная графика
• Компьютерная(машинная)
графика
воспроизводит изображение в случае,
когда исходной является информация
неизобразительной природы.
Можно сказать, что компьютерная графика
рисует, опираясь на формальные правила и
имеющийся набор средств
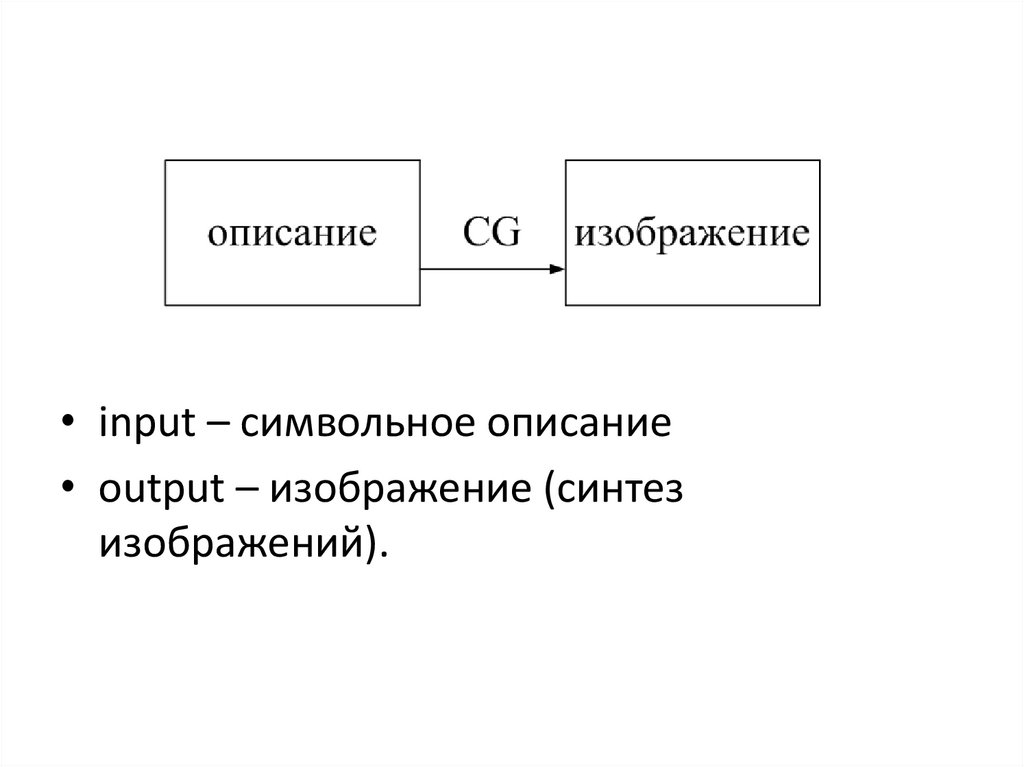
7.
• input – символьное описание• output – изображение (синтез
изображений).
8.
9. 2. Двумерное преобразование
Аналитическая геометрия – фундамент машграфики• любая точка на экране (бумаге) задается
координатами
• объекты описываются множеством координат и
связями между ними
Особенности системы координат экрана (СКЭ):
─ левая СК, центр которой находится в левом
верхнем углу
─ углы отсчитываются от оси Ox к оси Oy, то есть
по часовой стрелке
10.
Свойства аффинных преобразований:• сохраняются:
– прямые линии
– параллельность прямых
– отношение длин отрезков, лежащих на одной
прямой
– отношение площадей фигур
• любое аффинное преобразование может быть
представлено
как
последовательность
простейших операций: сдвиг, поворот и
масштабирование
11. Преобразования точки
• Сдвиг(x, y) – старые координаты
(x’, y’) – новые координаты
Tx, Ty – константы сдвига вдоль осей x и y
x’ = x + Tx
y’ = y + Ty
Например, x = 2, y = 3
Tx = 3, Ty = 2
x’ = 5, y’ = 5
12.
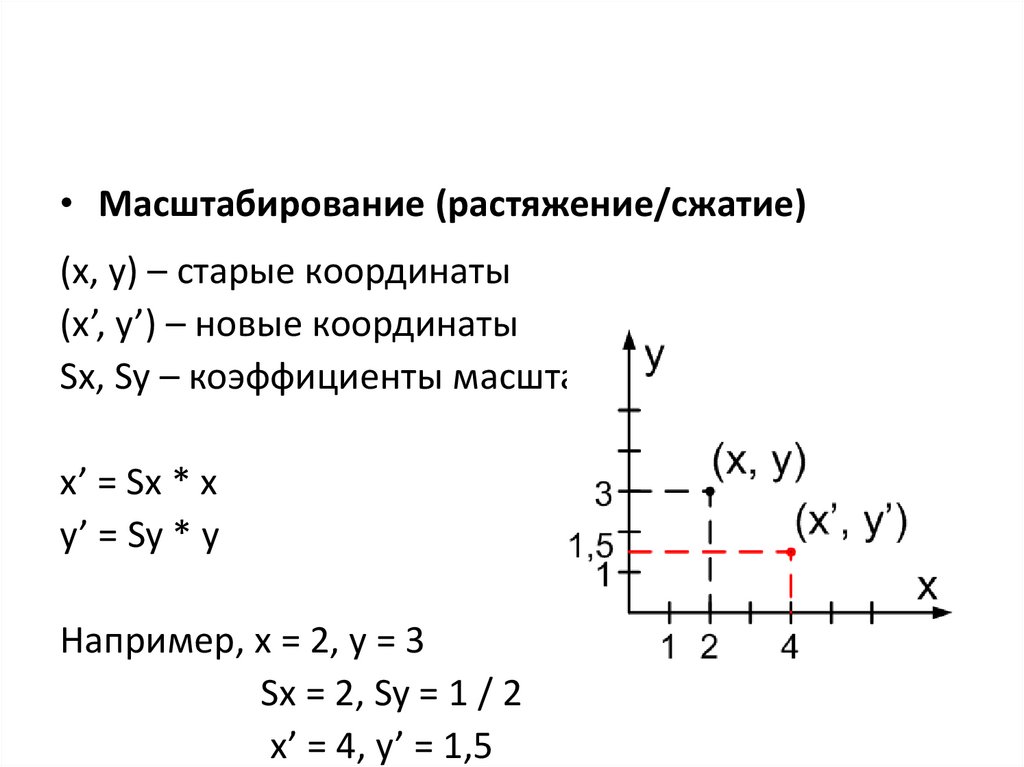
• Масштабирование (растяжение/сжатие)(x, y) – старые координаты
(x’, y’) – новые координаты
Sx, Sy – коэффициенты масштабирования
x’ = Sx * x
y’ = Sy * y
Например, x = 2, y = 3
Sx = 2, Sy = 1 / 2
x’ = 4, y’ = 1,5
13.
• зеркальное отражение (частный случаймасштабирования)
Sx
1
Sy
1
сама точка
-1
1
-1
1
-1
-1
ось Oy
ось Ox
центр O
14.
• ПоворотПоворот
всегда
происходит
относительно
начала координат в направлении против часовой
стрелки!
x = r * cos(α)
y = r * sin(α)
x’ = r * cos(α + β) =
= r * (cos(α) * cos(β) – sin(α) * sin(β)) =
= r * cos(α) * cos(β) – r * sin(α) * sin(β) =
= x * cos(β) - y * sin(β)
15.
x’ = x * cos(β) - y * sin(β)y’ = x * sin(β) + y * cos(β)
Пусть β – малый угол.
Тогда cos(β) ≈ 1
x’ = x * cos(β) - y * sin(β) = x – y * sin(β)
y’ = x * sin(β) + y * cos(β) = x * sin(β) + y
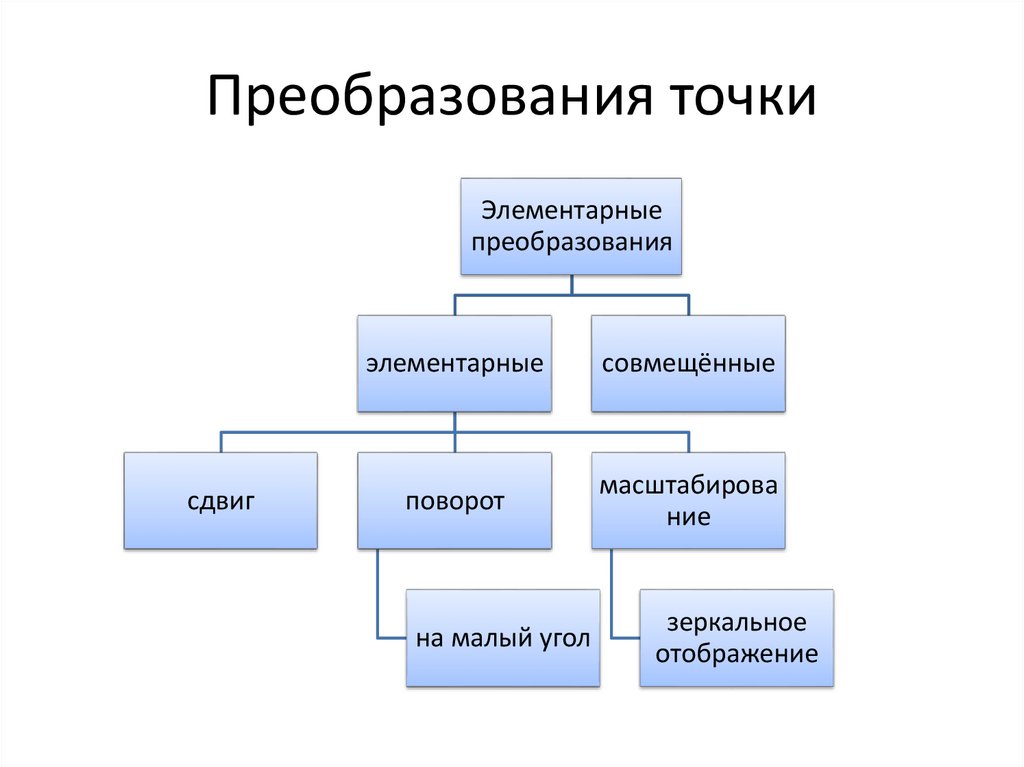
16. Преобразования точки
Элементарныепреобразования
сдвиг
элементарные
совмещённые
поворот
масштабирова
ние
на малый угол
зеркальное
отображение
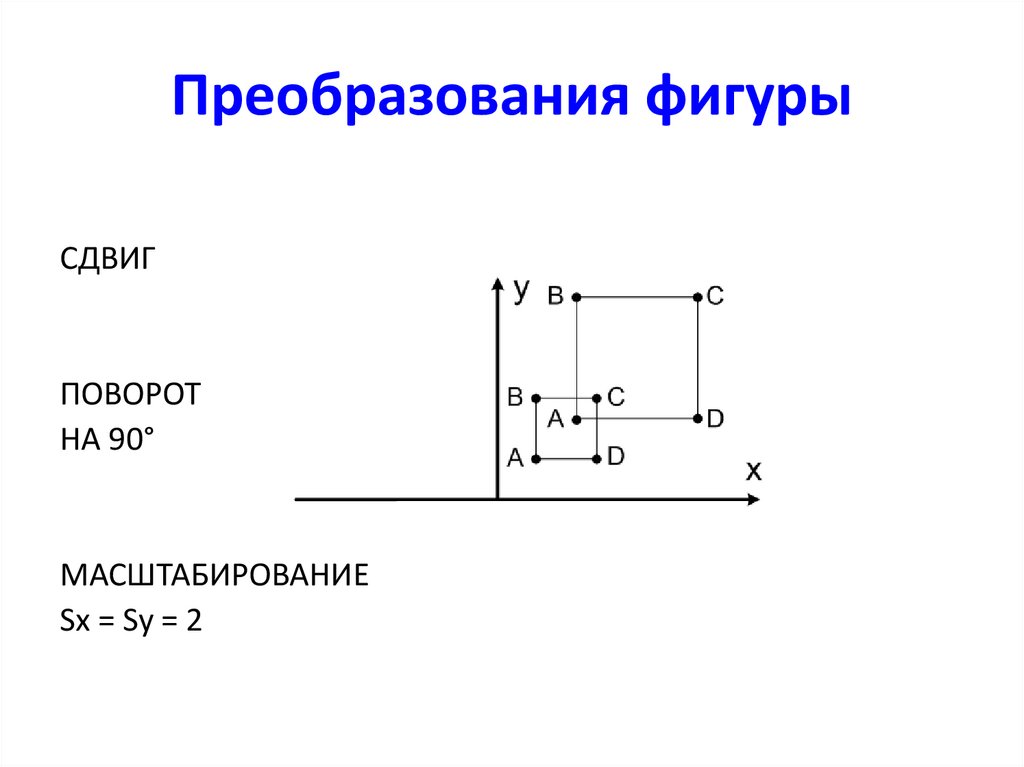
17. Преобразования фигуры
СДВИГПОВОРОТ
НА 90°
МАСШТАБИРОВАНИЕ
Sx = Sy = 2
18. Совмещенные двумерные преобразования
• Последовательно одно преобразование за другим(последовательно выполняем действия по
формулам)
• Суперпозиция
формул
(последовательно
подставляем формулы одна в другую, пока не
получим неприводимые формулы вида
A * x + B * y + C,
где A, B, C – коэффициенты, не зависящие от
точки)
• Матричный подход
19.
Однородные координатыПусть М – произвольная точка плоскости с
координатами (x, y).
Однородными координатами точки называется
тройка одновременно не равных 0 чисел x1, x2, x3,
если выполнены следующие соотношения:
x1
x2
x ,y
x3
x3
20.
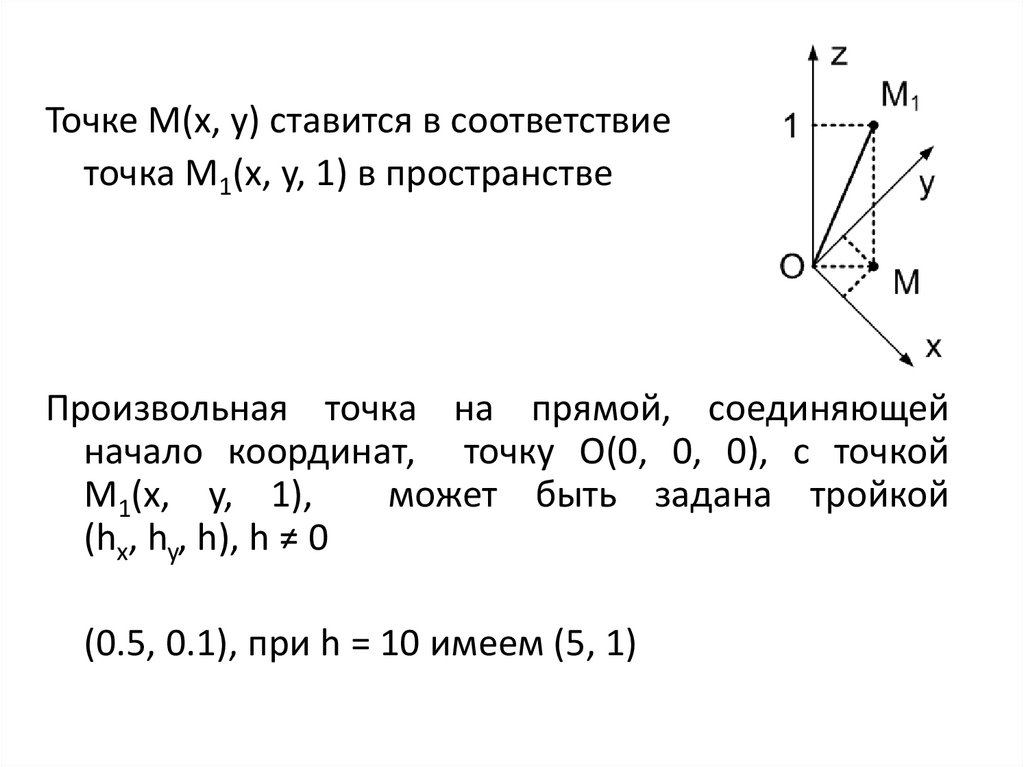
Точке M(x, y) ставится в соответствиеточка M1(x, y, 1) в пространстве
Произвольная точка на прямой, соединяющей
начало координат, точку О(0, 0, 0), с точкой
M1(x, y, 1),
может быть задана тройкой
(hx, hy, h), h ≠ 0
(0.5, 0.1), при h = 10 имеем (5, 1)
21. Матрицы преобразований
1 0 0[T] = 0 1 0
Tx Ty 1
Sx 0 0
[S] = 0 Sy 0
0 0 1
cos( a) sin( a) 0
[R] = sin( a) cos( a) 0
0
0
1
22.
x’ = x + Txy’ = y + Ty
1 0 0
[ x' y ' 1] [ x y 1] 0 1 0
Tx Ty 1
x’ = Sx * x
y’ = Sy * y
Sx 0 0
[ x' y ' 1] [ x y 1] 0 Sy 0
0 0 1
x’ = x * cos(β) - y * sin(β)
y’ = x * sin(β) + y * cos(β)
cos( ) sin( ) 0
[ x' y ' 1] [ x y 1] sin( ) cos( ) 0
0
0
1
23. Свойства элементарных преобразований
• сдвиги коммутативныTd1Td2 = Td2Td1
Tx1 = 1,5; Ty1 = 1;
Tx2 = 2,5; Ty2 = -0,5;
24. Свойства элементарных преобразований
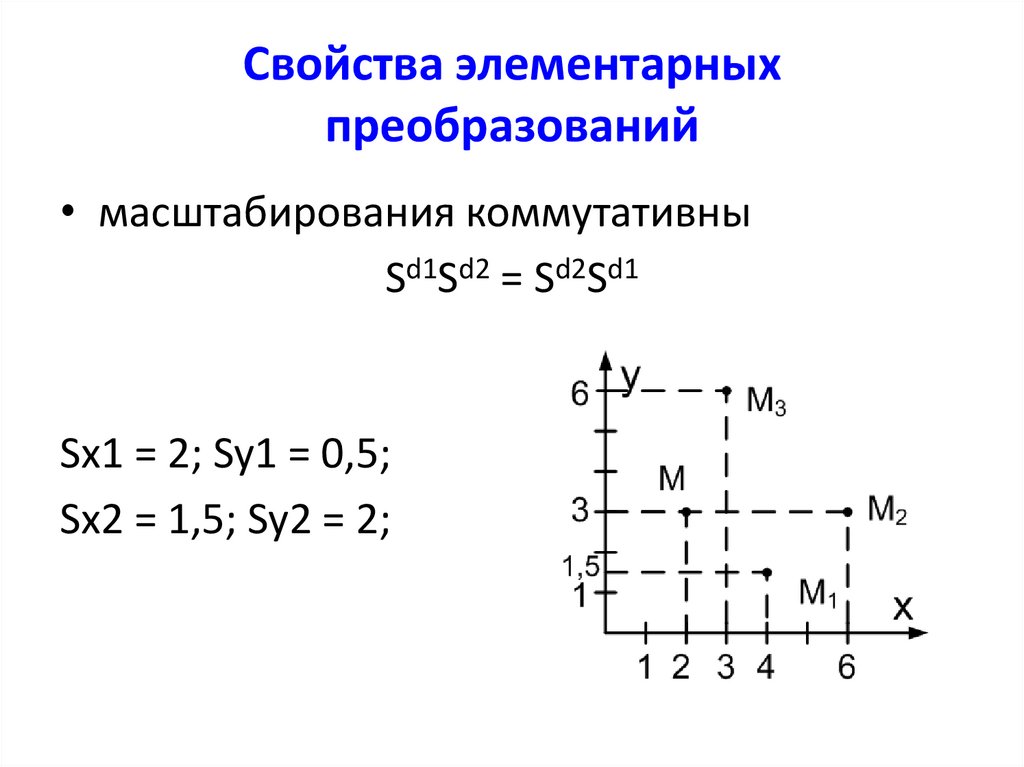
• масштабирования коммутативныSd1Sd2 = Sd2Sd1
Sx1 = 2; Sy1 = 0,5;
Sx2 = 1,5; Sy2 = 2;
25. Свойства элементарных преобразований
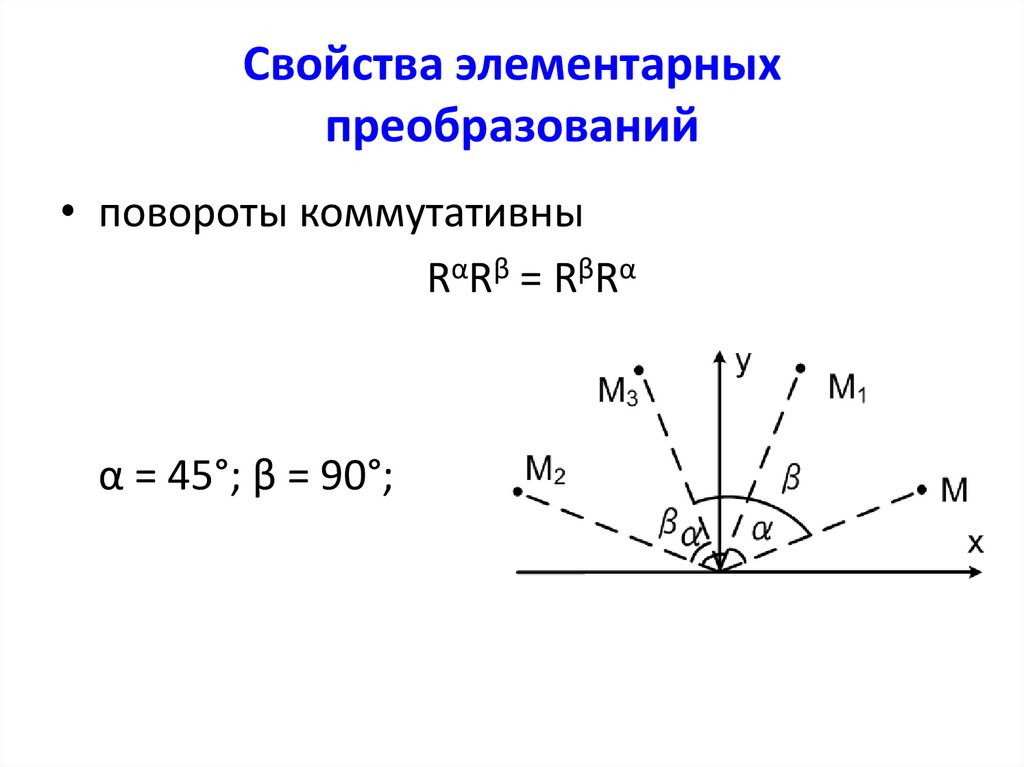
• повороты коммутативныRα Rβ = Rβ Rα
α = 45°; β = 90°;
26. Свойства элементарных преобразований
• два последовательных сдвига аддитивны(коэффициенты складываются)
Td1Td2 = Td1+d2
Tx1 = 1,5; Ty1 = 1;
Tx2 = 2,5; Ty2 = -0,5;
Tx = Tx1 + Tx2; Ty = Ty1 + Ty2;
27. Свойства элементарных преобразований
• два последовательных масштабированиямультипликативны (коэф-ты умножаются)
Sd1Sd2 = Sd1*d2
Sx1 = 2; Sy1 = 0,5;
Sx2 = 1,5; Sy2 = 2;
Sx = 2 * 1,5 = 3;
Sy = 0,5 * 2 = 1;
28. Свойства элементарных преобразований
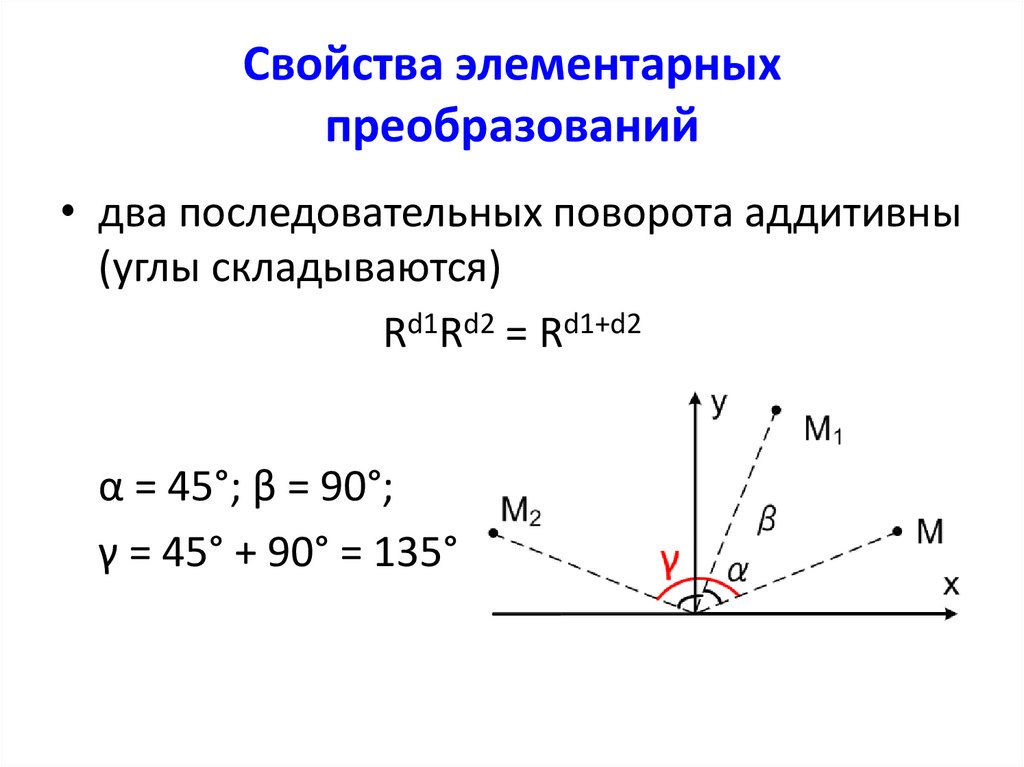
• два последовательных поворота аддитивны(углы складываются)
Rd1Rd2 = Rd1+d2
α = 45°; β = 90°;
γ = 45° + 90° = 135°
29. Свойства элементарных преобразований
• Масштабирование и поворот – коммутативны. Т.е.SR = RS
Sx = 2; Sy = 2;
α = 45°;
30. Свойства элементарных преобразований
• Сдвиг и масштабирование – не коммутативны. Т.е.TS ≠ ST
xM = 2; yM = 1;
Tx = 1; Ty = 1;
Sx = 2; Sy = 2;
31. Свойства элементарных преобразований
• Смещение и поворот – не коммутативны.Т.е
TR ≠ RT
xM = 2; yM = 1;
Tx = 2; Ty = 0;
α = 45°;
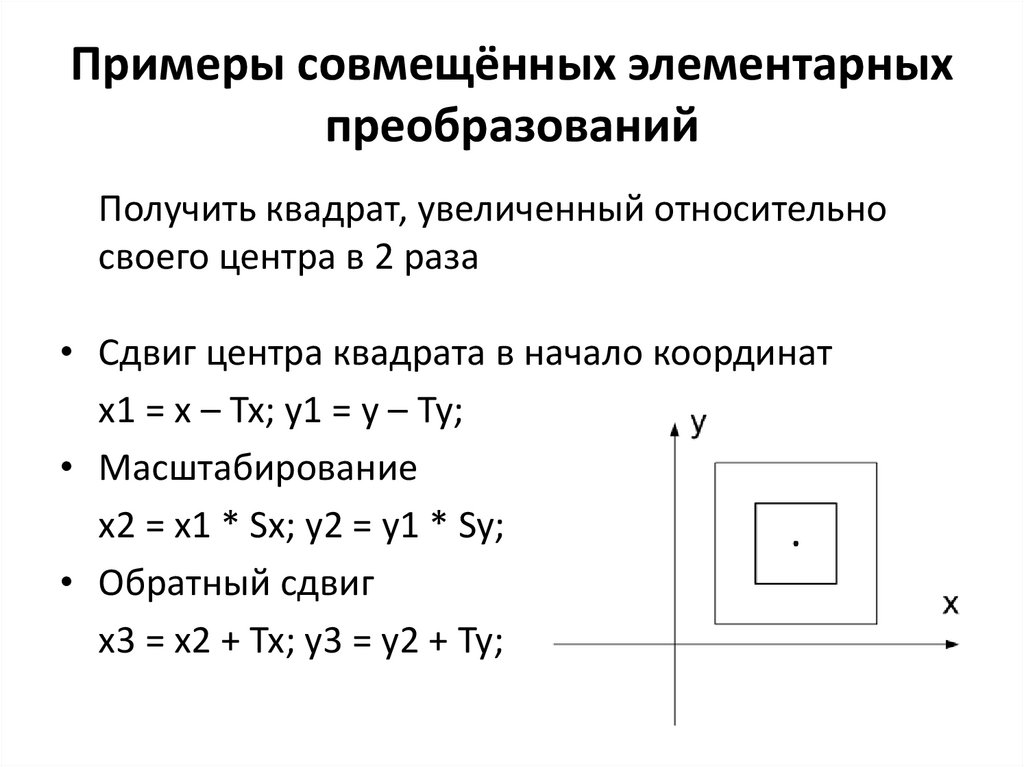
32. Примеры совмещённых элементарных преобразований
Получить квадрат, увеличенный относительносвоего центра в 2 раза
• Сдвиг центра квадрата в начало координат
x1 = x – Tx; y1 = y – Ty;
• Масштабирование
x2 = x1 * Sx; y2 = y1 * Sy;
• Обратный сдвиг
x3 = x2 + Tx; y3 = y2 + Ty;
33. Примеры совмещённых элементарных преобразований
Получить треугольник, который вращается относительноцентра О и увеличивается относительно своего центра
Сдвиг на TO
Поворот R
Сдвиг на TС
Масштабирование
Сдвиг на –TС
Сдвиг на –TO
34.
Матрица преобразования:[TO] [R] [TС] [S] [T-C] [T-O] =
= [TO] [R] [TС] [S] [T-D] = [V]
V – матрица совмещённого преобразования
[Xnew Ynew 1] = [X Y 1] [V]













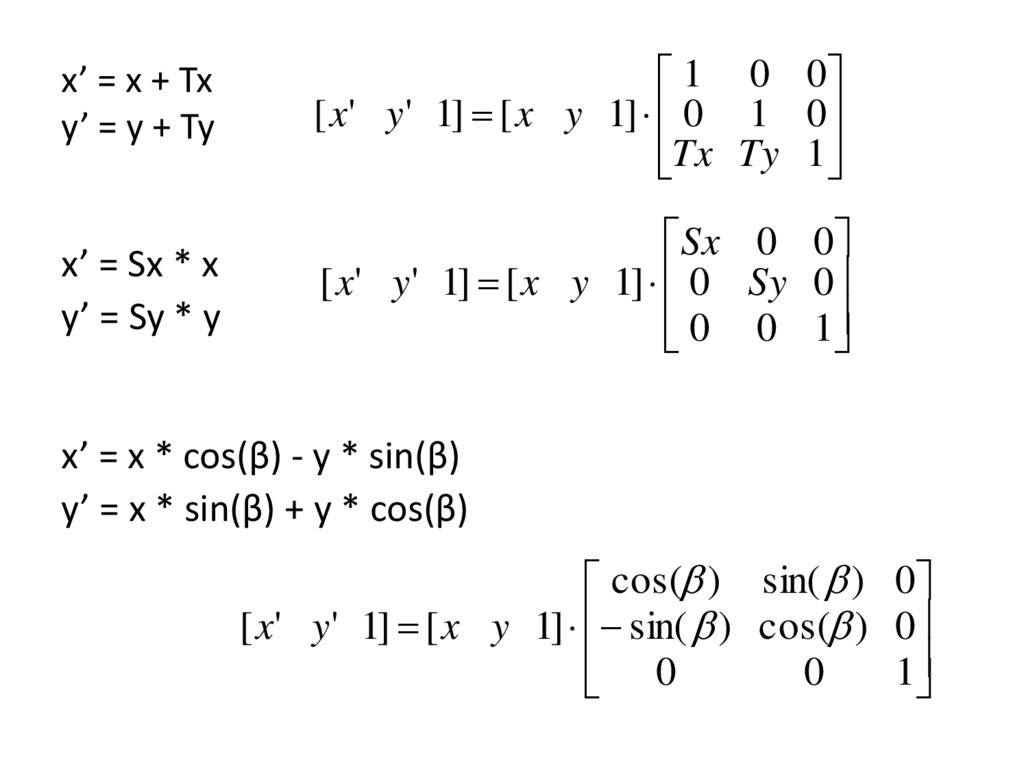








 Программирование
Программирование Информатика
Информатика