Система аксиом А. Д. Александрова

1.

Федеральное государственное образовательное учреждение высшего
образования Пензенский государственный университет
Педагогический институт им. В.Г. Белинского
Факультет физико-математических и естественных наук
Кафедра «Математическое образование»
СИСТЕМА АКСИОМ
А. Д. АЛЕКСАНДРОВА
Подготовили студентки группы 16ФПМ1
Кочетова Анастасия, Мещерякова Марина, Жирнова Даниэла.
Пенза, 2018

2.

Александр Данилович Александров
родился в деревне Волынь Рязанской
губернии 22 июля 1912 года.
Александр Данилович – советский и
российский математик, физик, философ,
альпинист.
Ректор
Ленинградского
государственного университета (1952—1964).
Заслуженный деятель науки и техники РСФСР.
Лауреат Сталинской премии. Мастер спорта
СССР.
В 1979-1983 годах им, А.Л. Вернером и
В.И. Рыжиком был создан курс геометрии для
средней школы, отличавшийся оригинальной
аксиоматикой и построенный под девизом «Назад – к Евклиду».
В 1987 году вышла в свет книга А.Д. Александрова
«Основания геометрии», в которой автор предлагает свою
аксиоматику евклидовой геометрии.

3.

Греческий ученый Евдем Родосский (IV в. до н. э.) писал:
«Геометрия была открыта
египтянами и возникла из измерения
земли. Это измерение было им
необходимо вследствие разливов
Нила, постоянно смывавших границы.
Нет ничего удивительного в том, что
эта наука, как и другие, возникла из
потребностей
человека.
Всякое
возникающее
знание
из
несовершенного состояния переходит
в совершенное. Зарождаясь путем
чувственного
восприятия,
оно
постепенно становится предметом
нашего рассмотрения и, наконец,
делается достоянием разума».

4.

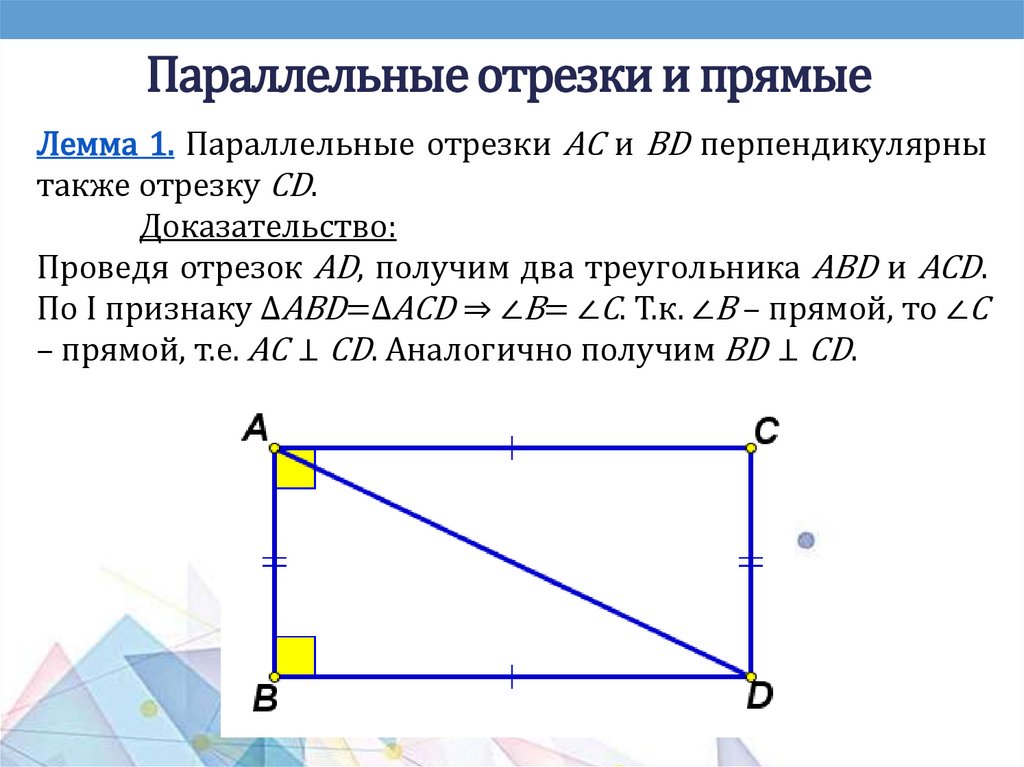
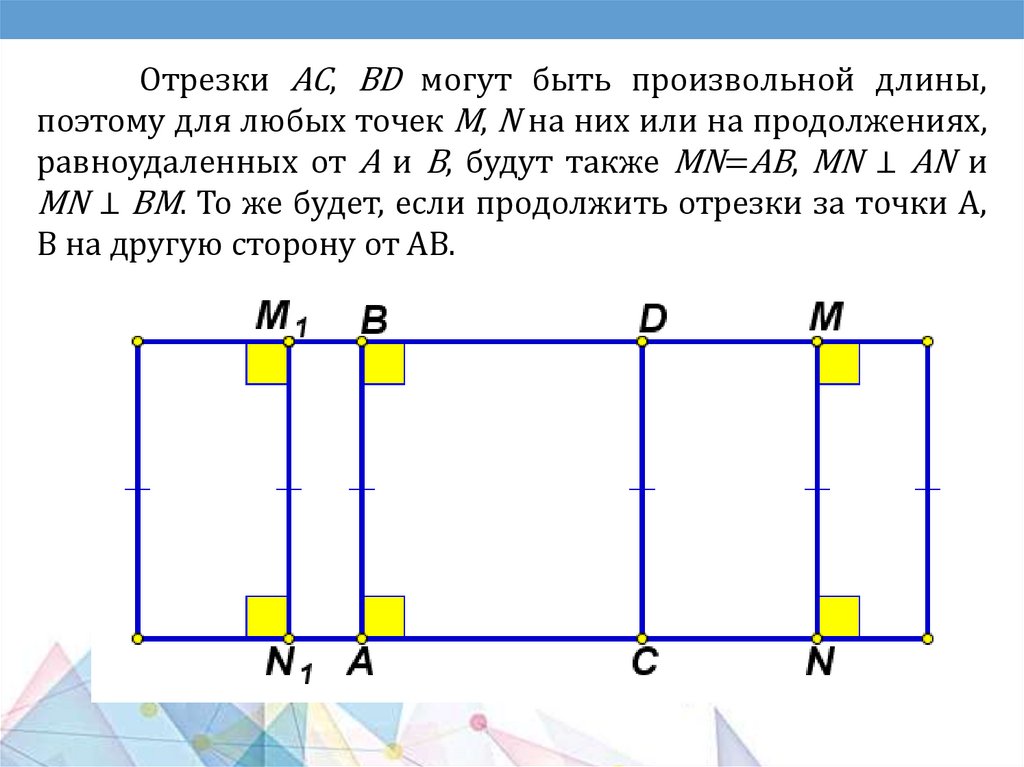
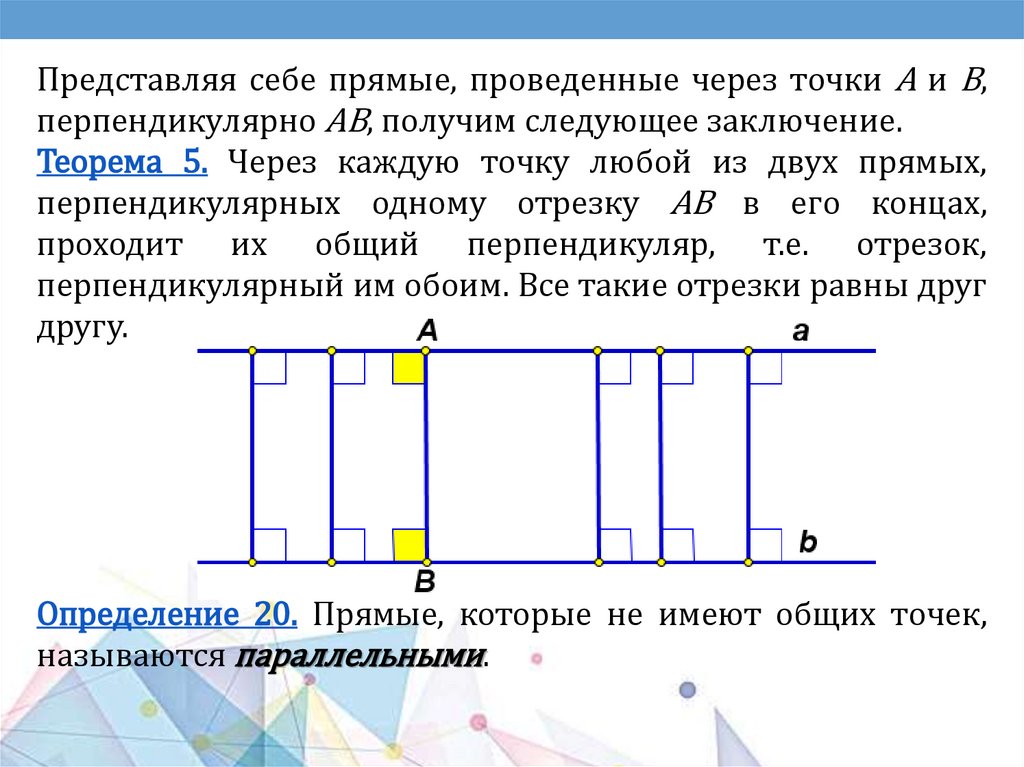
Особенности аксиоматики А. Д. Александрова
1. В начале предлагается система аксиом
планиметрии, развивается геометрия на плоскости,
обсуждаются вопросы основания планиметрии и лишь
затем, появляется система аксиом геометрии евклидова
пространства.
2. Основными объектами аксиоматики планиметрии
являются
точки
и
отрезки,
что
соответствует
практическим основаниям геометрии, где фигурируют
именно отрезки, а не бесконечные прямые.
3. «. . . кроме точек и отрезков рассматриваются
такие фигуры, как, например, окружность. Однако кажется,
ни в одной из известных аксиоматик не вводится понятие
фигуры так, чтобы под него попадала хотя бы окружность».

5.

Система аксиом Александрова
математическую структуру
σ