Система аксиом Вейля

1.

Федеральное государственное образовательное учреждение высшего образования
Пензенский государственный университет
Педагогический институт им. В.Г. Белинского
Факультет физико-математических и естественных наук
Кафедра «Математическое образование»
Система аксиом Вейля
Подготовили студентки группы 16ФПМ1
Жилкина Ольга и Панова Юлия.
Пенза, 2018

2.

Содержание
1. Общие вопросы аксиоматики
Система аксиом Вейля
Требования к системе
2. Аксиоматическое построение теории
3. Непротиворечивость системы аксиом
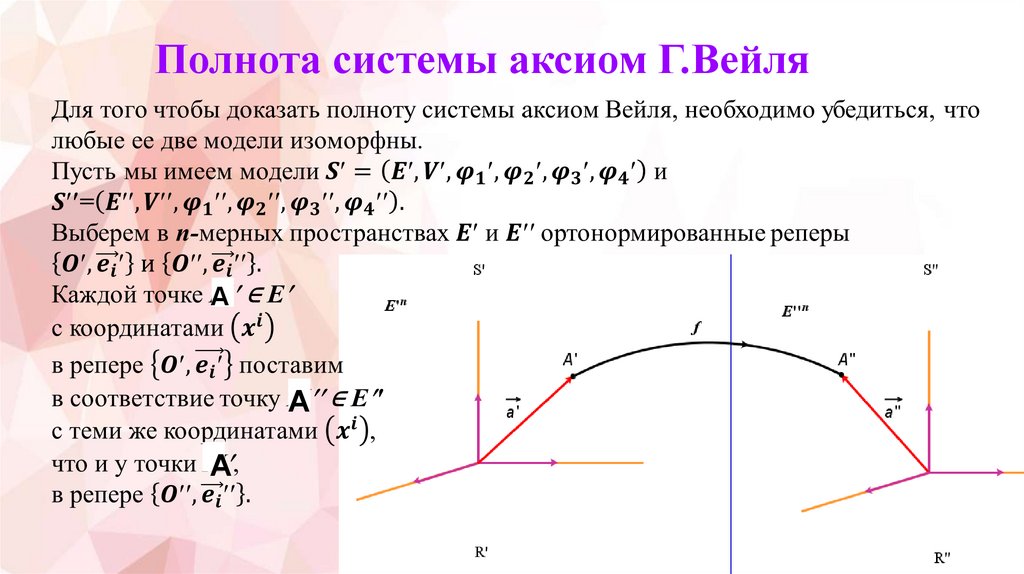
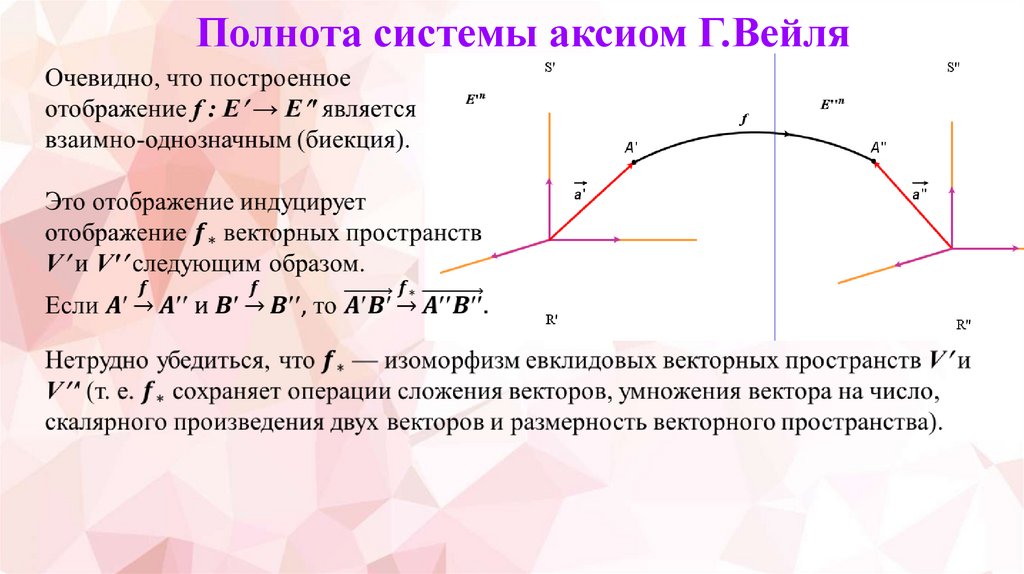
4. Полнота системы аксиом
5. Об эквивалентности систем аксиом Д.Гильберта и
Г.Вейля

3.

Математика играет весьма
существенную роль в формировании
нашего духовного облика. Занятие
математикой – подобно
мифотворчеству, литературе или
музыке – это одна из наиболее
присущих человеку областей его
творческой деятельности, в которой
проявляется его человеческая
сущность, стремление к
интеллектуальной сфере жизни,
являющейся одним из проявлений
мировой гармонии.
Герман Вейль

4.

Герман Клаус Хуго Вейль (9.XI.1885 - 8.XII.1955).
Родился в Эльмсхорне (Германия). В 1908 г. окончил
Геттингенский университет, в том же году защитил
диссертацию и получил степень доктора философии.
С 1908 до 1913 г. читал лекции в Геттингенском
университете в качестве приват-доцента. С 1913 по
1930 г. - профессор Цюрихского политехнического
института. В 1930 - 1933 гг. работает в Геттингенском
университете, а с 1933 по 1955 г. - в Принстонском
институте перспективных исследований (США).
Исследования относятся к теории групп,
дифференциальной геометрии, теории интегральных
и дифференциальных уравнений, математической
логике, основаниям математики, квантовой механике, теории относительности.
Международная премия имени Н.И.Лобачевского присуждена в 1927 году за цикл работ
по геометрии и теории линейных представлений групп.

5.

Общие вопросы аксиоматики
Система аксиом Вейля
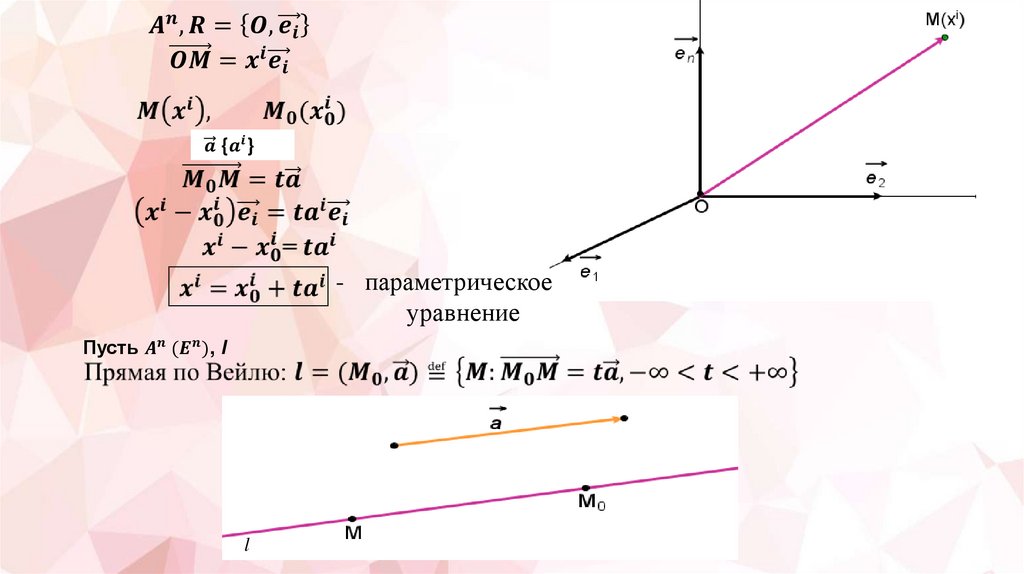
В 1918 году Г. Вейлем была предложена точечно-векторная аксиоматика евклидовой
геометрии.
Основными объектами в этой аксиоматике являются точки и векторы.
A,B,C, … ─ точки
─ векторы
Основные отношения
в системе аксиом Вейля
определяются основными операциями:
─ сложением векторов;
─ умножением векторов на число;
─ скалярным произведением;
─ операцией внешней суммы (откладывание вектора от точки).

6.

Система аксиом Вейля
Таким образом, система аксиом Вейля
математическую структуру:
─ множество точек;
─ множество векторов;
определяет

7.

Аксиоматическое построение теории
Система аксиом Вейля поделена на 5 групп:
I группа. Аксиомы сложения векторов (4 аксиомы)
II группа. Аксиомы умножения вектора на действительное
число (4 аксиомы)
III группа. Аксиомы размерности (2 аксиомы)
Аксиомы первых трех групп определяют n-мерное линейное (или
векторное) пространство.
IV группа. Аксиомы скалярного произведения (4 аксиомы)
Аксиомы первых четырех групп определяют n-мерное евклидово
векторное пространство.
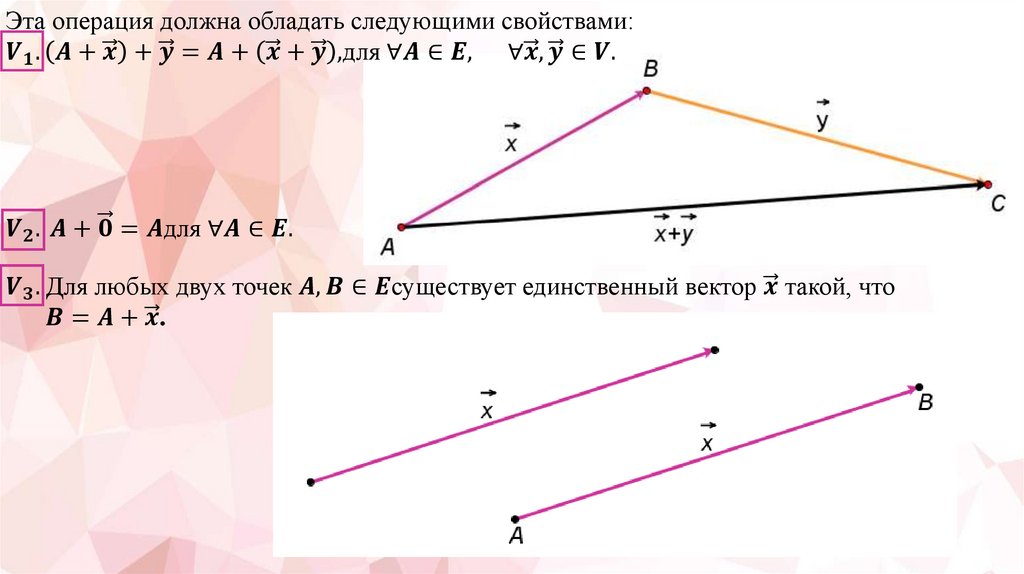
V группа. Аксиомы откладывания вектора от точки (3 аксиомы)
Аксиомами всех пяти групп определяется n-мерное евклидово
пространство.

8.

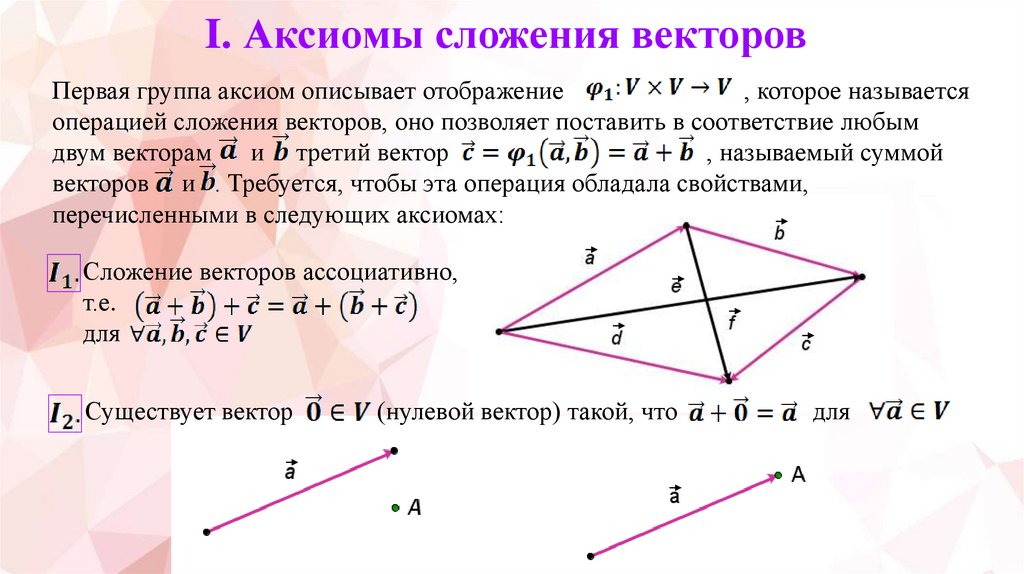
I. Аксиомы сложения векторов
Первая группа аксиом описывает отображение
, которое называется
операцией сложения векторов, оно позволяет поставить в соответствие любым
двум векторам
и третий вектор
, называемый суммой
векторов и . Требуется, чтобы эта операция обладала свойствами,
перечисленными в следующих аксиомах:
Сложение векторов ассоциативно,
т.е.
для
Существует вектор
(нулевой вектор) такой, что
для

9.

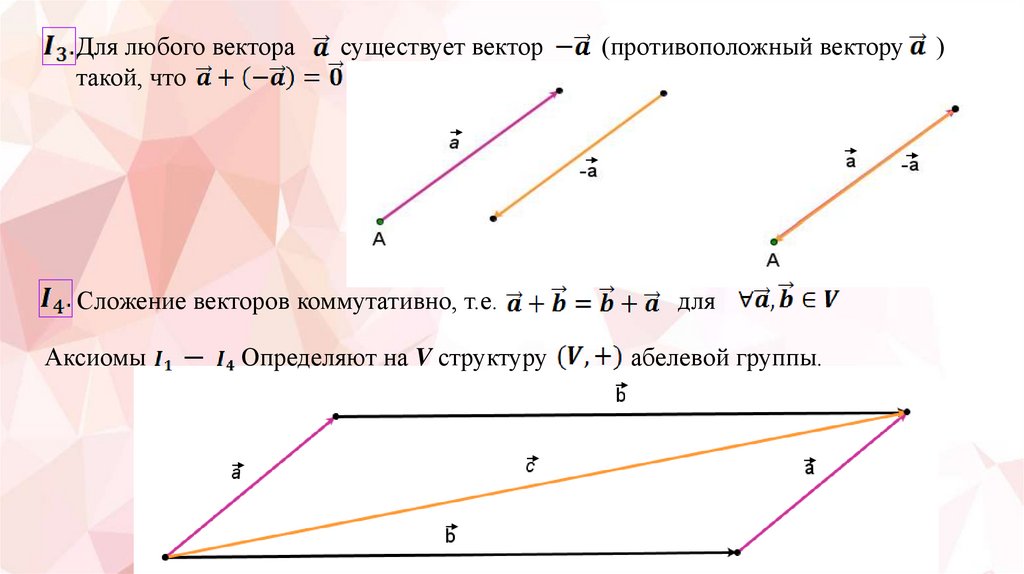
Для любого вектора
такой, что
существует вектор
Сложение векторов коммутативно, т.е.
Аксиомы
─
Определяют на V структуру
(противоположный вектору
для
абелевой группы.
)

10.

II. Аксиомы умножения вектора на число
Вторая группа аксиом описывает отображение
, называемое
операцией умножения вектора на действительное число. Каждому вектору
и
числу
однозначно сопоставляется вектор
, называемый
произведением вектора на число.
Операция умножения вектора на действительное число удовлетвoряeт следующим
аксиомам.

11.

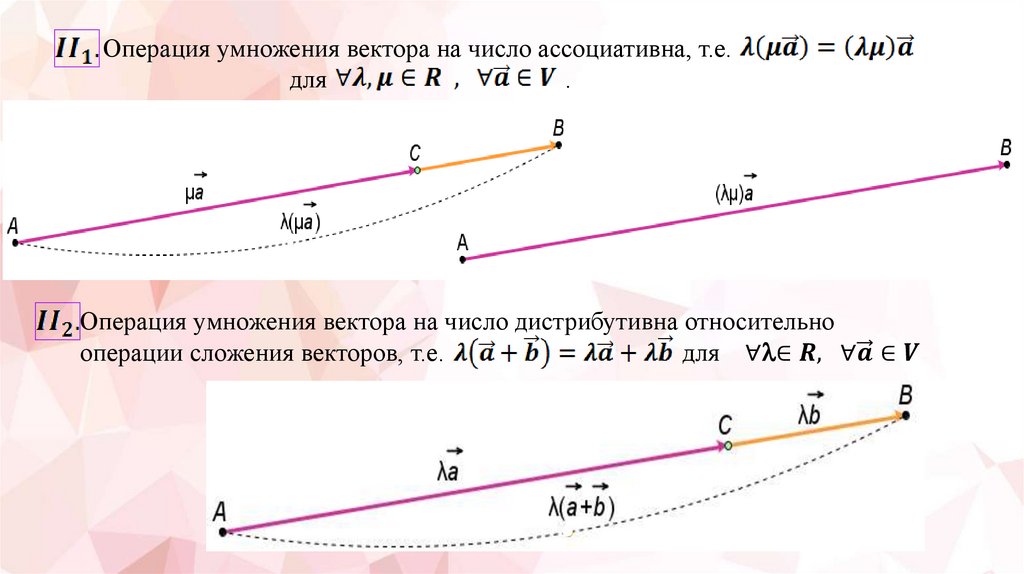
Операция умножения вектора на число ассоциативна, т.е.
для
.
Операция умножения вектора на число дистрибутивна относительно
операции сложения векторов, т.е.
для ∀ ∈