Особенности гиперзвуковых скоростей. Лекция 24

1.

Аэрогазодинамика
Особенности
гиперзвуковых скоростей
Лекция 24
1

2. 24.1. Особенности гиперзвуковых течений

Гиперзвуковой диапазон скоростей – при числах Маха
М > 5 (скорость звука много меньше скорости потока).
Возникает ряд качественно новых явлений:
1. Возмущения скорости, малые по сравнению со
скоростью невозмущенного потока, становятся
соизмеримыми с местной скоростью звука dV ~ a.
Поэтому малое изменение скорости приводит к
значительному изменению энтальпии и других
параметров состояния p, , T .
dp
2 dV
dp
V
Ур. Бернулли в дифференциальной форме VdV
0
p
p
V
dp
2 dV
k M
Тогда
. Аналогично для других параметров
p
V
dV da
k 1 2 dV
d
dV dT
k 1 M 2
M
M2
T
V
a
2
V
V
2

3.

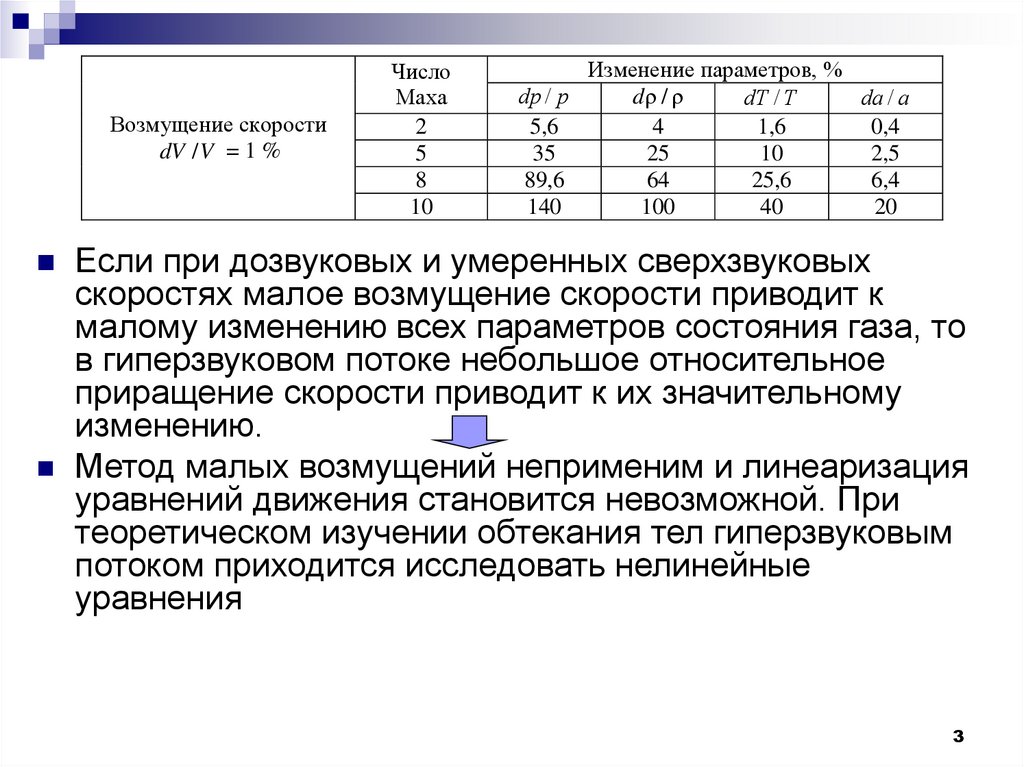
Возмущение скорости
dV / V = 1 %
Число
Маха
2
5
8
10
Изменение параметров, %
dp / p
d /
dT / T
da / a
5,6
4
1,6
0,4
35
25
10
2,5
89,6
64
25,6
6,4
140
100
40
20
Если при дозвуковых и умеренных сверхзвуковых
скоростях малое возмущение скорости приводит к
малому изменению всех параметров состояния газа, то
в гиперзвуковом потоке небольшое относительное
приращение скорости приводит к их значительному
изменению.
Метод малых возмущений неприменим и линеаризация
уравнений движения становится невозможной. При
теоретическом изучении обтекания тел гиперзвуковым
потоком приходится исследовать нелинейные
уравнения
3

4.

2. При обтекании тел гиперзвуковым потоком
происходит взаимодействие скачка уплотнения с
пограничным слоем.
3. Повышение температуры за скачком уплотнения и
в пограничном слое может привести к изменению
термодинамических свойств и химического состава
воздуха вследствие диссоциации и ионизации газа.
4. Время пребывания молекул около тела настолько
мало, что может быть меньше времени релаксации,
т. е. состояние газа у поверхности тела будет
неравновесным - уравнения газовой динамики
решаются совместно с уравнениями, описывающими
физико-химические процессы в газе, что влияет на
структуру скачка уплотнения и распределение
параметров состояния газа.
4

5.

5. В условиях сильно возросших температур для
расчета параметров течения необходимо учитывать
реальность газов в связи с изменением величины
показателя адиабаты. Так при М = 20 температура
заторможенного газа за прямым скачком уплотнения
для идеальной среды составит 18 000 К, а в реальной
среде с учетом вышесказан-ного она имеет значение
всего лишь 6 820 К.
Число Маха за прямым скачком уплотнения M2 ид 0,38,
тогда как M2 реал 0,29 .
6. При температурах Т > 5000 … 6000 К происходит
ионизация воздуха и вблизи поверхности тела
образуется плазменный поток
5

6. 24.2. Приближенная теория Ньютона

При гиперзвуковых скоростях полета распределение
давления по поверхности тела в области до миделевого сечения позволяет определить приближенная теория
Ньютона.
Модель среды:
а) газообразная среда состоит из не
взаимодействующих между собой частиц;
б) скорость движения частиц среды вплоть до
столкновения их с поверхностью равна скорости
набегающего невозмущенного потока V ;
в) при столкновении частиц с поверхностью
нормальная составляющая скорости Vn V sin
становится равной нулю, а касательная составляющая
остается неизменной.
6

7.

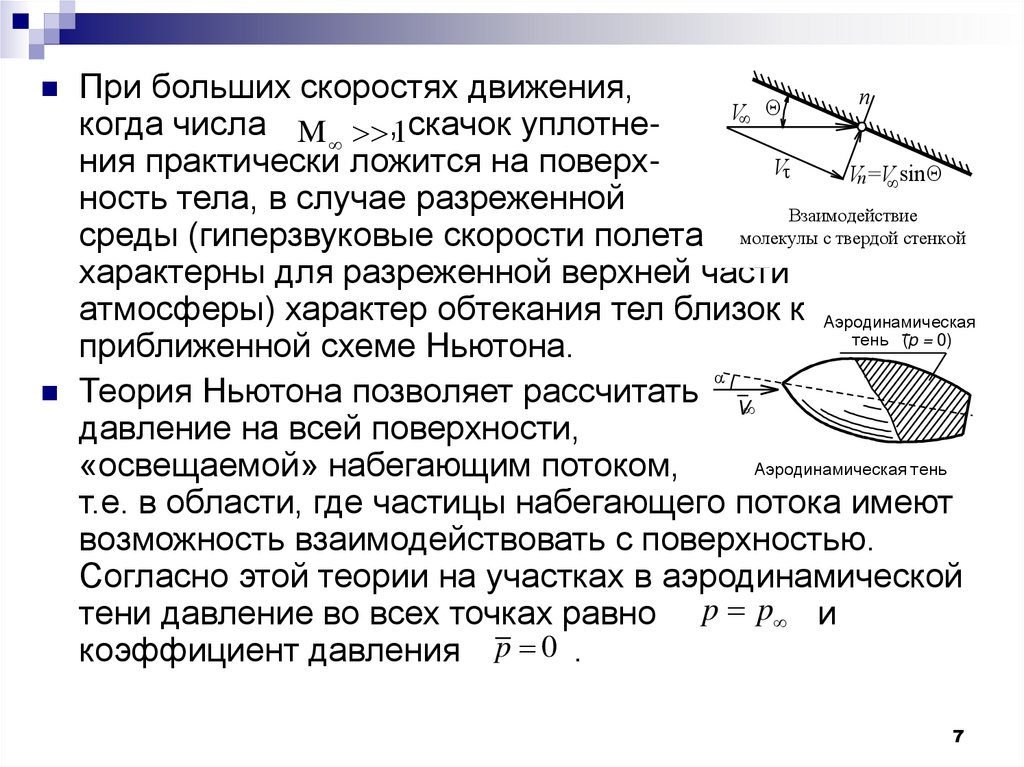
При больших скоростях движения,
n
V
когда числа M ,1скачок уплотнения практически ложится на поверхV
Vn =V sin
ность тела, в случае разреженной
Взаимодействие
среды (гиперзвуковые скорости полета молекулы с твердой стенкой
характерны для разреженной верхней части
атмосферы) характер обтекания тел близок к Аэродинамическая
тень (p = 0)
приближенной схеме Ньютона.
a
Теория Ньютона позволяет рассчитать V
давление на всей поверхности,
Аэродинамическая тень
«освещаемой» набегающим потоком,
т.е. в области, где частицы набегающего потока имеют
возможность взаимодействовать с поверхностью.
Согласно этой теории на участках в аэродинамической
тени давление во всех точках равно p p и
коэффициент давления p 0 .
7

8.

На элемент поверхности dS с местным углом атаки
массовый расход которого
,а
количество движения равно
. После соударения с поверхностью нормальная составляющая
скорости становится равной нулю. Изменение
количества движения приравняем к импульсу силы
давления:
.
p p
Общее выражение для коэффициента
p
q
давления
В нашем случае: p 2sin 2 - следствие теории Ньютона
Коэффициент давления в данной точке поверхности
тела зависит только от местного угла атаки поверхности
и не зависит ни от числа Маха, ни от формы
обтекаемого тела - НЕДОСТАТОК
8

9. 24.3. Уточненная теория Ньютона

Для учета влияние формы тела и числа Маха на
распределение давления по поверхности тела
произвольной формы в исходную формулу Ньютона
вводится уточнение. Считаем, что значение
коэффициента давления p в некоторой фиксированной точке тела, рассчитанное по приближенной
формуле, должно совпадать с точным значением в
этой точке p *, имеющей местный угол атаки
поверхности *:
p* sin 2
p
sin 2 *
Фиксированные (характерные) точки для разных
геометрических форм:
9

10.

* = 90о
* = к
а
б
Для заостренного тела – точка у острия тела (а); в
данном случае *= к , - углу при вершине
обтекаемого тела (или углу конусности наконечника), а
*
величина pравна
pдля какой-либо образующей
этого наконечника.
Для затупленных тел – передняя критическая точка,
располагающаяся за прямым скачком уплотнения, для
*
которой sin 1 , а давление равно давлению
торможения за прямым скачком p02 , и расчетная
формула примет вид:
p p sin 2
02
10