Арксинус, арккосинус, арктангенс, арккотангенс

1.

Тема урока: «Арксинус,
арккосинус, арктангенс,
арккотангенс».
Цели урока.
Повторить графический способ
решения уравнений; доказать
теорему о корне; познакомиться с
понятиями аркфункции; научиться
вычислять значения этих функции.

2.

y
у=х2
y=5
x
х2=5
х1= 5
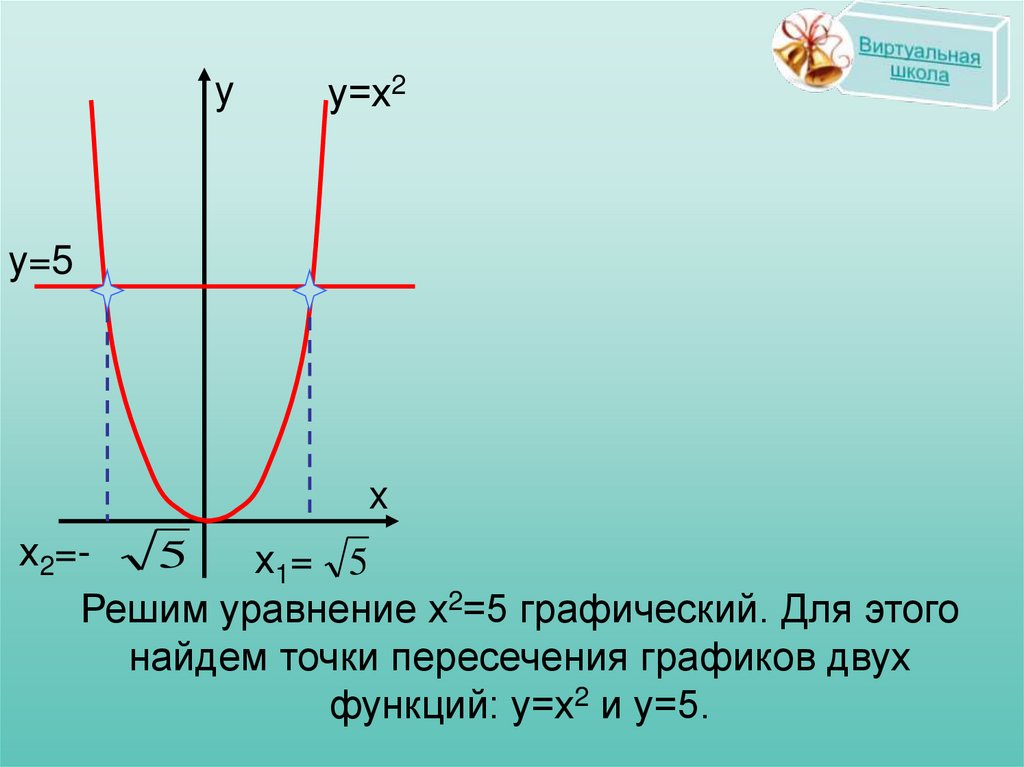
Решим уравнение х2=5 графический. Для этого
найдем точки пересечения графиков двух
функций: у=х2 и у=5.

3.

y
у=а
y= f(х)
x
D(f)
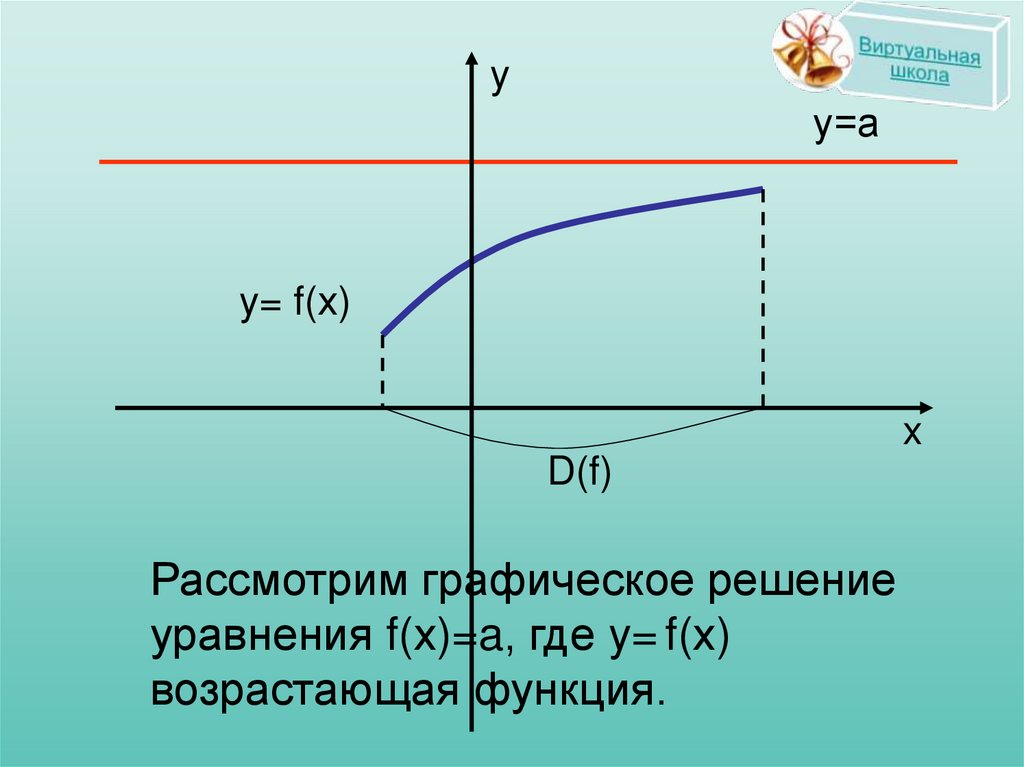
Рассмотрим графическое решение
уравнения f(х)=a, где y= f(х)
возрастающая функция.

4.

y
у=а
b
x
D(f)
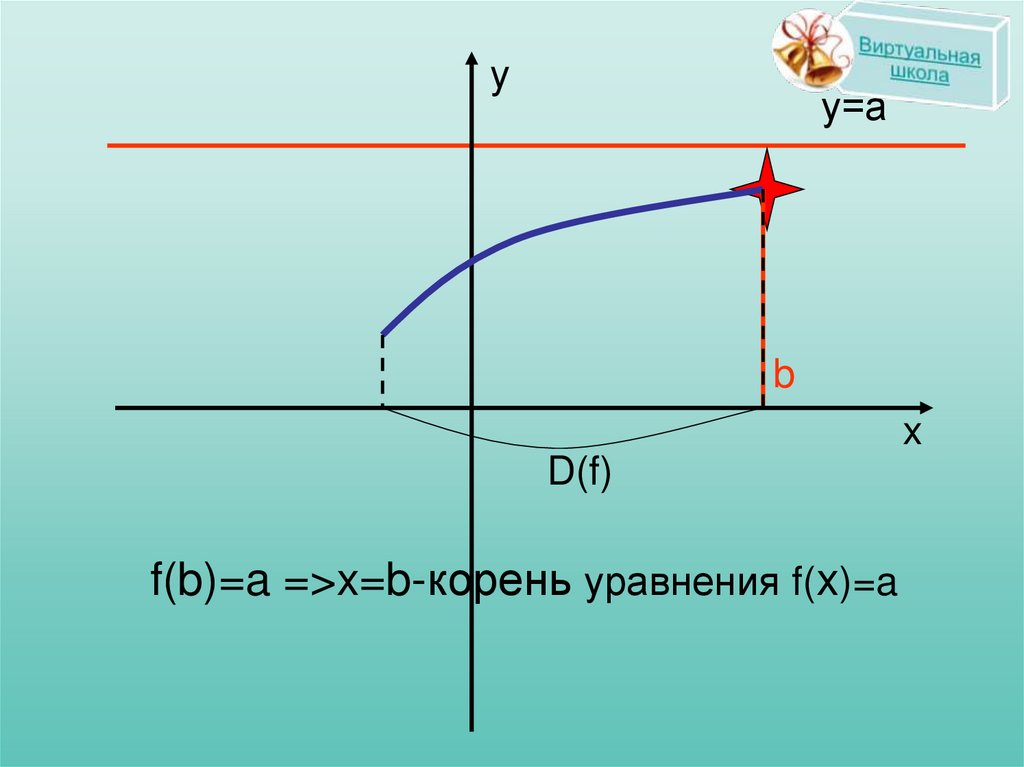
f(b)=a =>x=b-корень уравнения f(x)=a

5.

y
у=а
b
x
D(f)
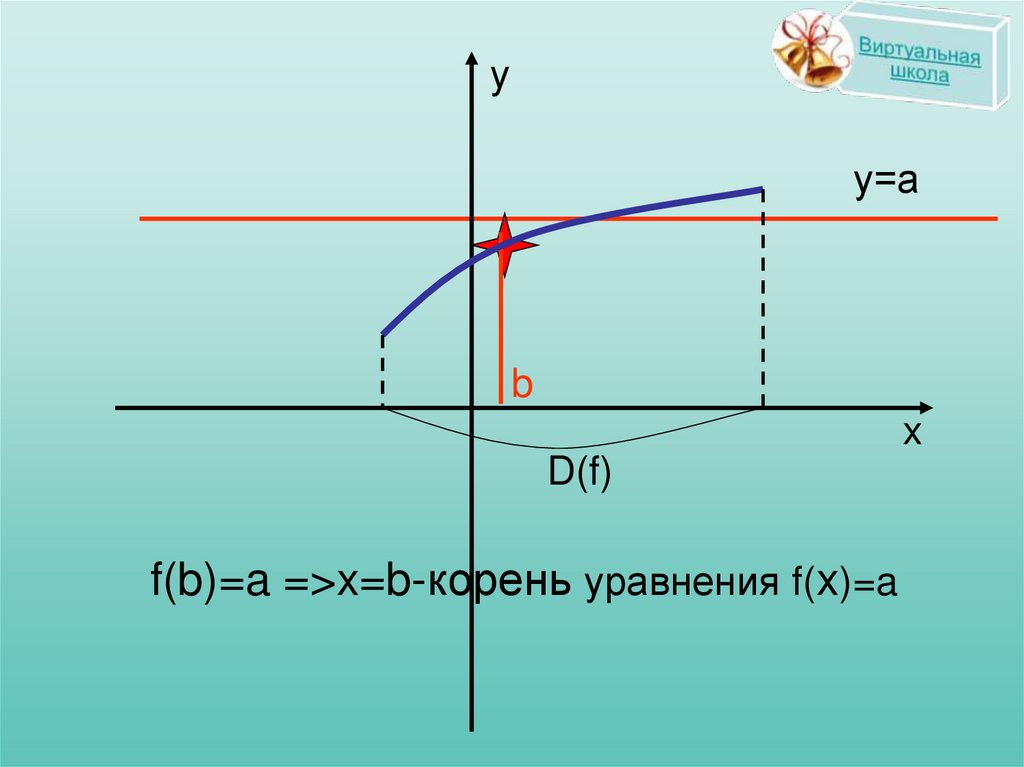
f(b)=a =>x=b-корень уравнения f(x)=a

6.

y
у=а
b
x
D(f)
f(b)=a =>x=b-корень уравнения f(x)=a

7.

y
у=а
b
x
D(f)
f(b)=a =>x=b-корень уравнения f(x)=a

8.

y f(x) ≠a
у=а
x
D(f)
Уравнение f(x)=a корней не имеет

9.

Теорема (о корне). Стр 64.

10.

y
у=а
b
x
D(f)
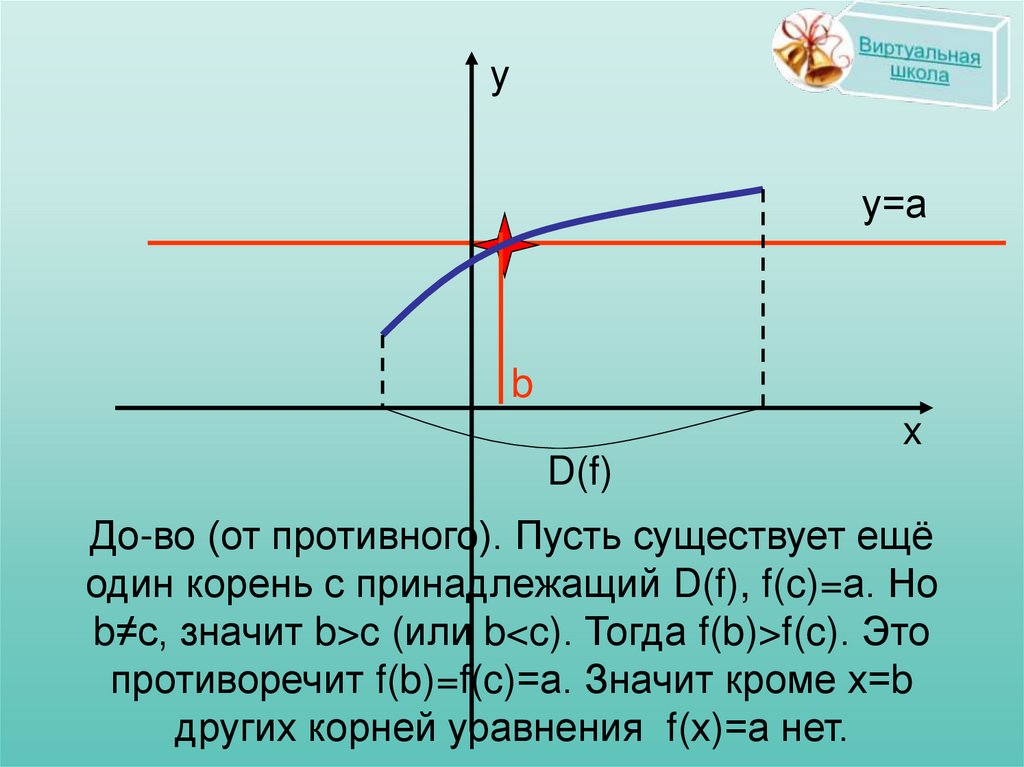
До-во (от противного). Пусть существует ещё
один корень с принадлежащий D(f), f(c)=а. Но
b≠с, значит b>c (или b<c). Тогда f(b)>f(c). Это
противоречит f(b)=f(c)=а. Значит кроме х=b
других корней уравнения f(х)=а нет.

11.

Арксинус
y
y=sin x
1
π/2
-π/2
x
-1
Функция y=sin x на отрезке [-π/2; π/2] возрастает и
принимает все значения от -1 до 1.

12.

Арксинус
y=a
1
π/2
-π/2
b
x
-1
По теореме о корне уравнение sin x=a на
отрезке [-π/2; π/2] имеет единственный корень
b при аЄ[-1;1]

13.

Арксинус
y=a
1
π/2
-π/2
b=arcsin a
x
-1
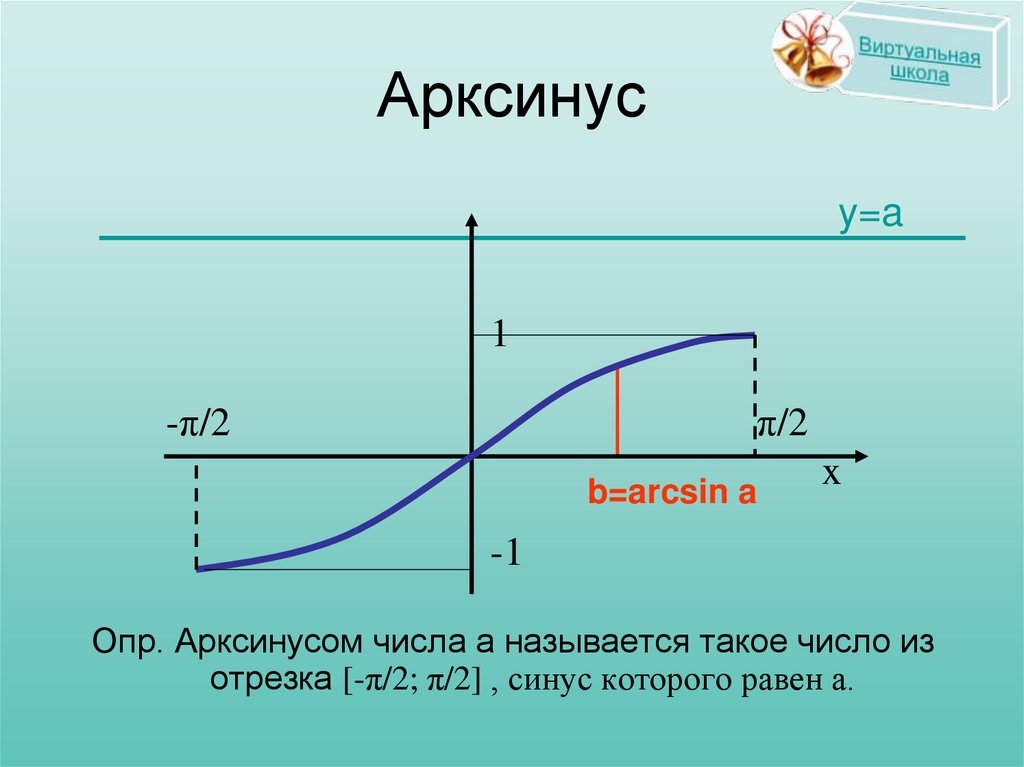
Опр. Арксинусом числа а называется такое число из
отрезка [-π/2; π/2] , синус которого равен а.

14.

Арксинус
y=1
1
π/2
-π/2
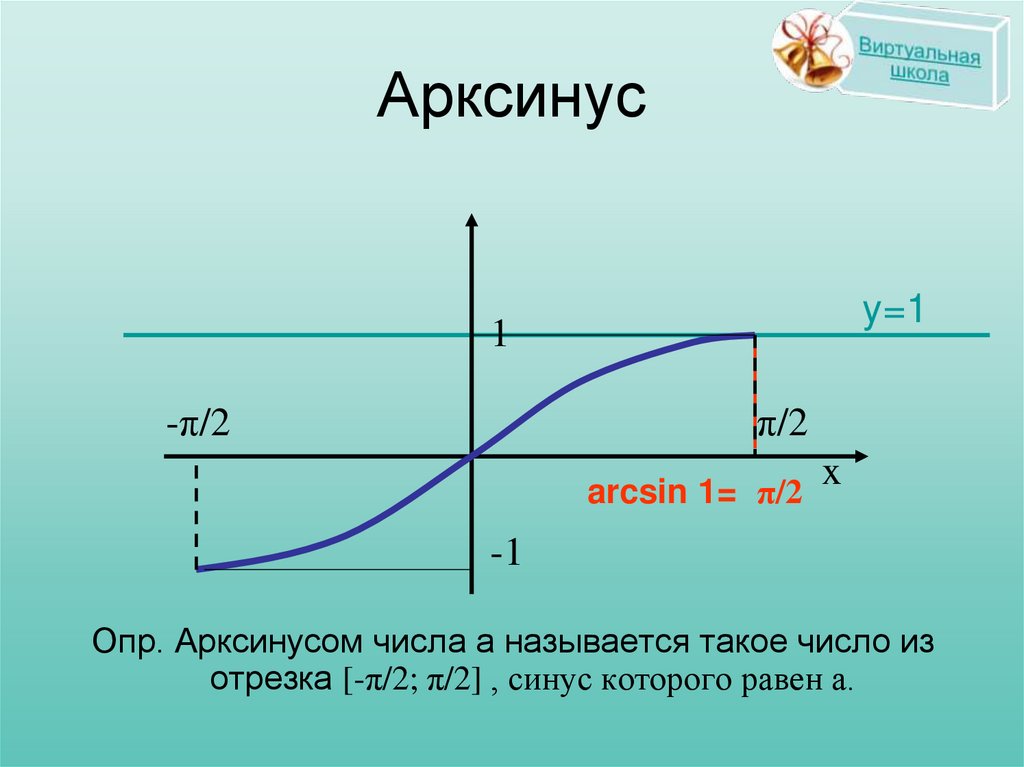
arcsin 1= π/2
x
-1
Опр. Арксинусом числа а называется такое число из
отрезка [-π/2; π/2] , синус которого равен а.

15.

Арксинус
y=
1
0,5
π/2
-π/2
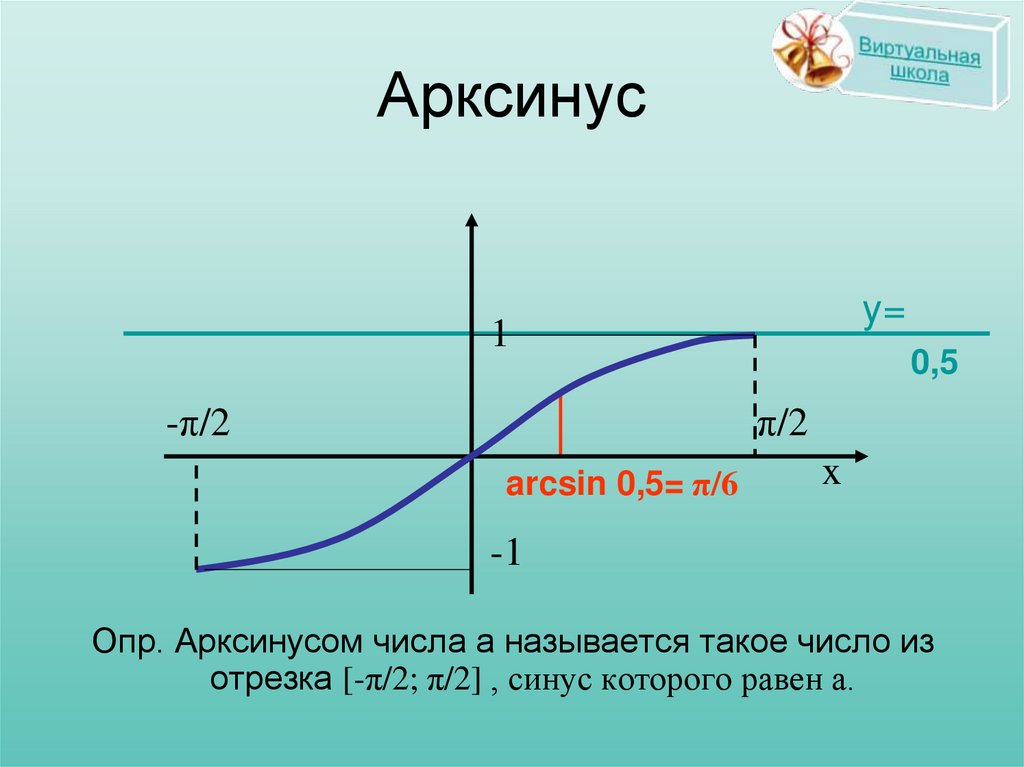
arcsin 0,5= π/6
x
-1
Опр. Арксинусом числа а называется такое число из
отрезка [-π/2; π/2] , синус которого равен а.

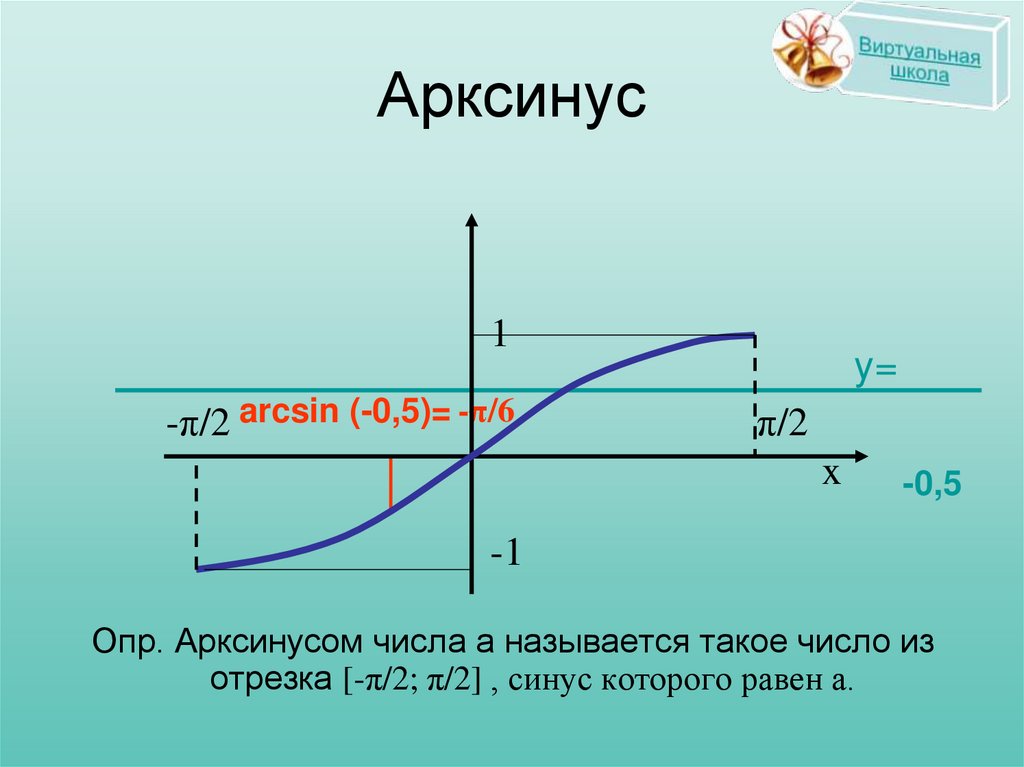
16.

Арксинус
1
-π/2 arcsin (-0,5)= -π/6
y=
π/2
x
-0,5
-1
Опр. Арксинусом числа а называется такое число из
отрезка [-π/2; π/2] , синус которого равен а.

17.

Арксинус
1
π/2
-π/2
xy=
arcsin (-1)=-π/2
-1
-1
Опр. Арксинусом числа а называется такое число из
отрезка [-π/2; π/2] , синус которого равен а.

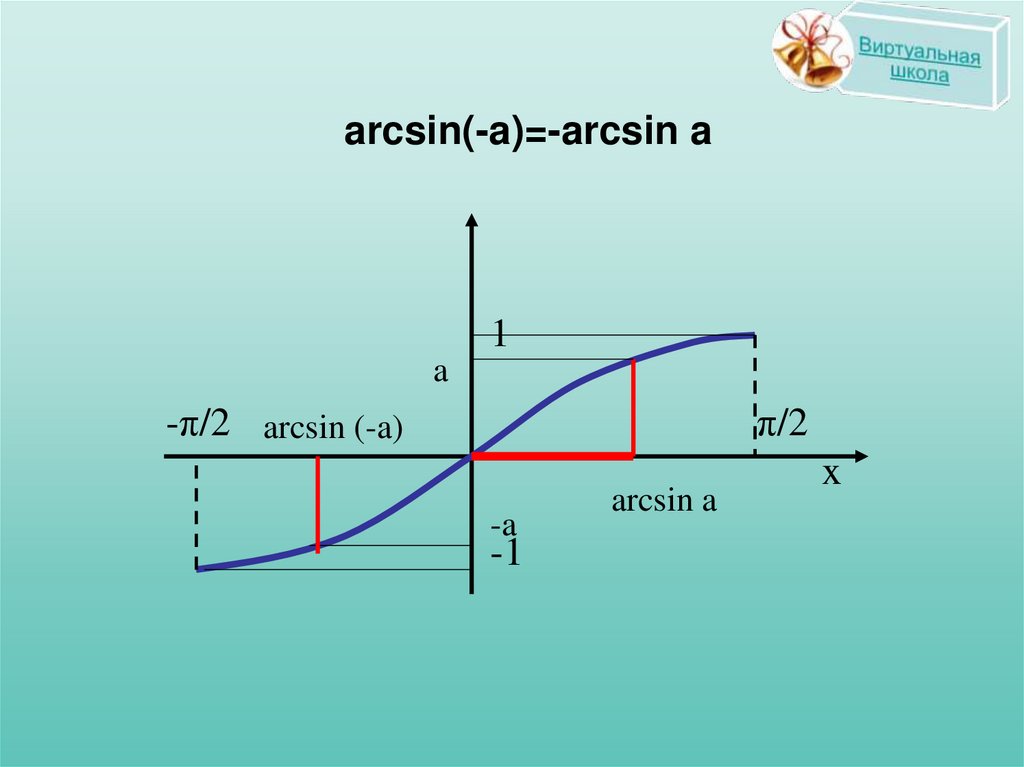
18.

arcsin(-a)=-arcsin a
1
a
π/2
-π/2 arcsin (-a)
-a
-1
arcsin a
x

19.

2
arcsin
2
2
arcsin(
)
2
3
arcsin
2
3
arcsin(
)
2
arcsin 0 0
arcsin 3
π/4
-π/4
π/3
-π/3
не существует
Почему?
Почему?
Почему?
Почему?
Почему?

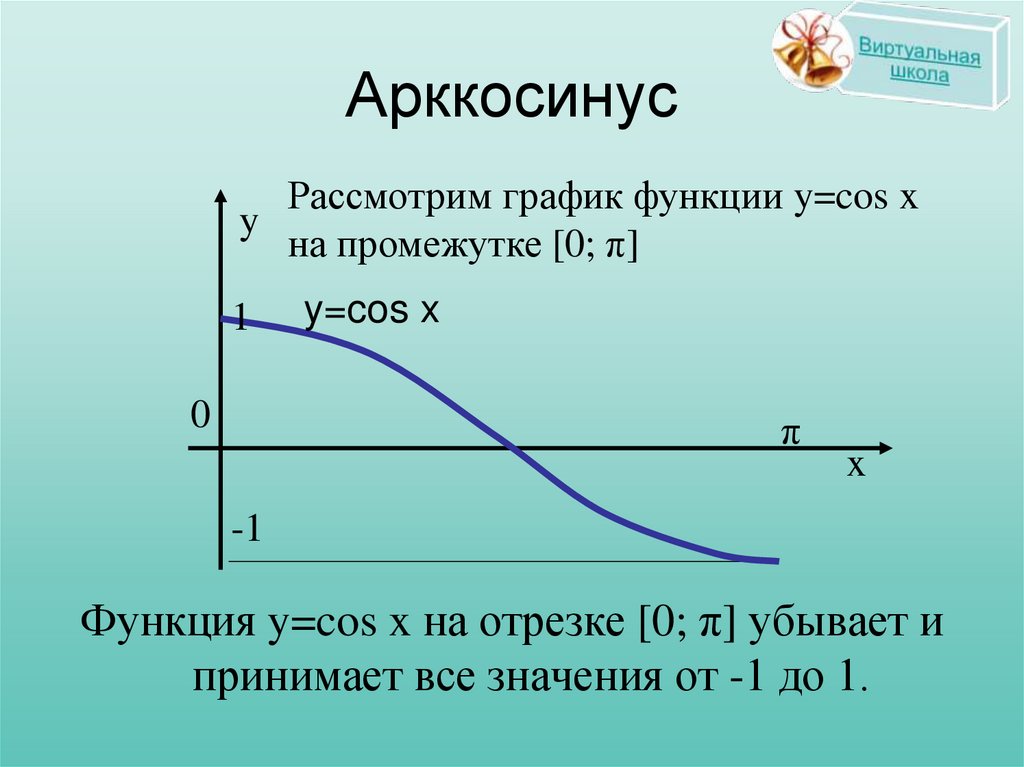
20.

Арккосинус
Рассмотрим график функции y=cos x
y
на промежутке [0; π]
1
0
y=cos x
π
x
-1
Функция y=cos x на отрезке [0; π] убывает и
принимает все значения от -1 до 1.

21.

Арккосинус
y=a
y
1
0
π
b
x
-1
По теореме о корне уравнение cos x=a на
отрезке [0; π] имеет единственный
корень b при аЄ[-1;1]

22.

Арккосинус
y=a
y
1
0
π
b=arccos a
x
-1
Опр. Арккосинусом числа а называется такое
число из отрезка [0; π] , косинус которого равен а.

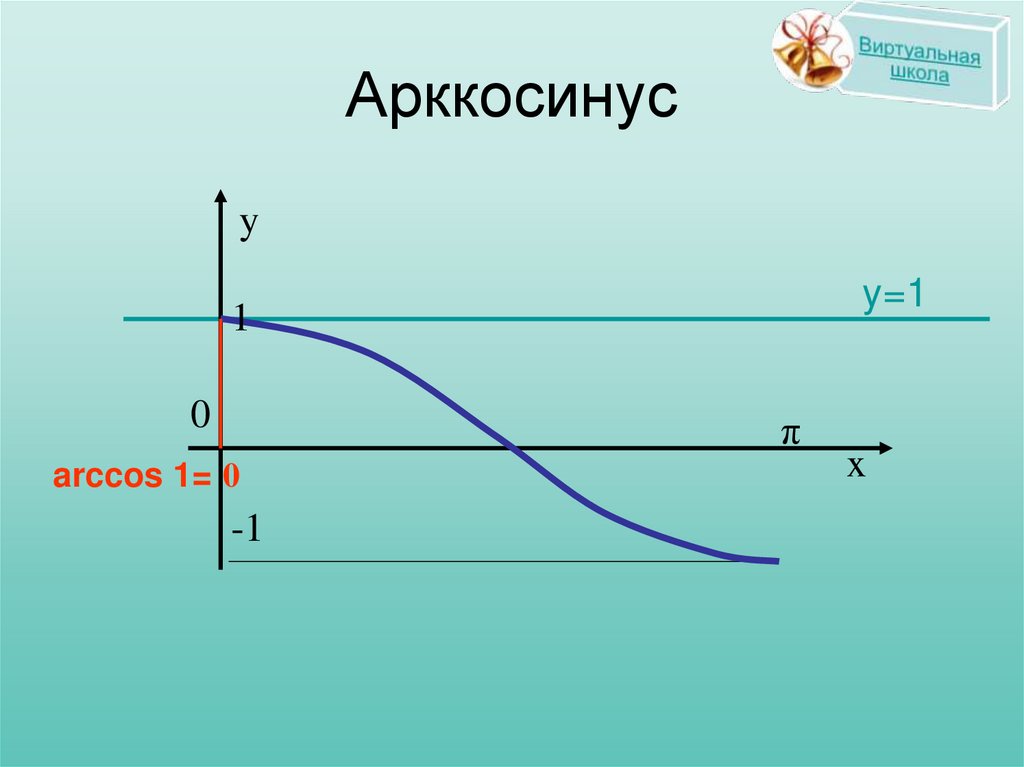
23.

Арккосинус
y
y=1
1
0
π
arccos 1= 0
-1
x

24.

Арккосинус
y
y=0,5
1
0
π/3
arccos 0,5= π/3
-1
π
x

25.

Арккосинус
y
1
y=-0,5
0
2π/3
-1
arccos (-0,5)= 2π/3
π
x

26.

Арккосинус
y
1
0
π
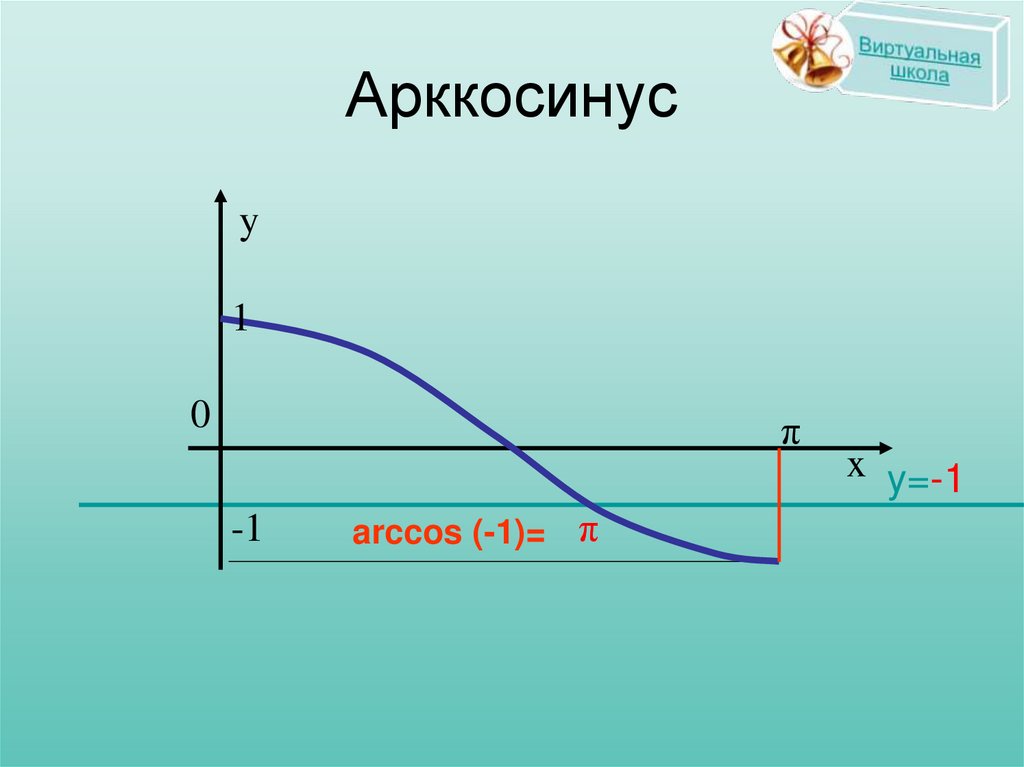
-1
arccos (-1)= π
x y=-1

27.

2
arccos
π/4
2
2
arccos(
) 3π/4
2
3
arccos
π/6
2
3
arccos(
) 5π/6
2
arccos 0 π/2
arccos
2
не существует
Почему?
Почему?
Почему?
Почему?
Почему?

28.

В понятиях арктангенса и арккотангенса
попробуйте разобраться
самостоятельно. Для этого перейдите
по ссылке http://vschol.ru/urok/urok1.htm
и нажмите на «Начать
самостоятельную работу»
Запишите домашнее задание.
•п8, №118(а,б), 119(а,б), 121(а,б),
122(а,б).
•Из Интернета – по ссылке
http://vschol.ru разобрать 6 тестов
по подготовке к ЕГЭ.