Похожие презентации:
Арксинус и арккосинус
1.
Тема урокаУчитель математики
Абакарова Раисат Алибековна
МКОУ «Уркарахская многопрофильная гимназия им. А. Абубакара"
Дахадаевского района Республика Дагестан
2.
• Цели и задачи урока:• Сформировать знания обучающихся о
понятиях: арксинус и арккосинус числа.
• Научить вычислять их значения по
таблице.
• Развивать мышление, память,
вычислительные навыки, навыки
самоконтроля и взаимоконтроля.
• Воспитывать ответственность,
самостоятельность, трудолюбие.
• Совершенствовать навыки устного
счета
3.
.Блицопрос
2. От чего зависит значение
1. Кофункция тангенса –
это…?
косинус
функции?
От
аргумента
3. Мера измерения угла?
градус,
радиан
4. Какой функции недостает: синус,
тангенс
косинус, котангенс?
5. Значение тригонометрических
период
функций повторяется через?
4.
.6. y = соs x –
тригонометрическая…
функция
7. Как называется график функции y =
sin x ?
cинусоида
8.
(0;?) – Что это?
ордината
9. Он не только в земле, но и в корень
математике.
аксиома
10. Предложение, требующее
доказательства?
5.
.11. Отношение противолежащего
катета к гипотенузе - это
синус
12. y = sin x - нечетная функция,
y = соs x четная
13. Функции синус, косинус,
тангенс и котангенс
изучаются в разделе математики,
который называется… тригонометрия
6. Решение задач
Устный счет:19+200=
:(-3)=
-13=
+6=
: (-0,2)=
7. Решение задач
На рисунке показано изменение температуры воздуха напротяжении трех суток. По горизонтали указывается дата и
время суток, по вертикали — значение температуры в
градусах Цельсия. Определите по рисунку наименьшую
температуру воздуха 16 октября.
8. Решение задач
На диаграмме показан средний балл участников 10 стран втестировании по математике. Найдите средний балл
участников из Болгарии.
9. Решение задач
Найдите площадь трапеции, вершины которой имеюткоординаты (1;1), (10;1), (9;8), (4;8)
10. Решение задач
Определите знак выражения:0
0
0
0
1) sin 105 cos 37 tg85 ctg93
0
0
0
2) sin 197 cos134 tg 74 ctg190
0
11.
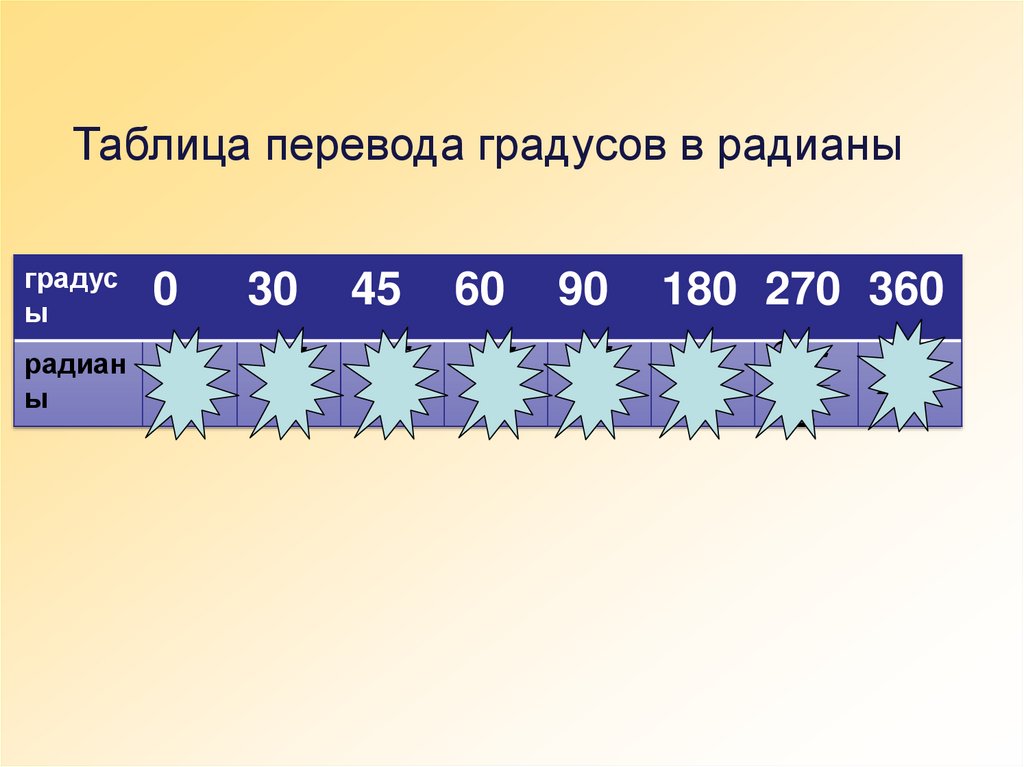
Таблица перевода градусов в радианыградус
ы
радиан
ы
0
0
30
6
45
4
60
3
90
2
180 270 360
3 2
2
12.
Таблица некоторых значенийтригонометрических функций
функци
я
0
30
45
60
sin 0
cos 1
1
2
2
2
2
2
3
2
1
2
tg 0
ctg
90
180
1 0
3
0
1
2
1
3 0
3 1
1
3 1 3 0
270
360
1 0
0 1
0
0
13.
Тригонометрические функции – этоматематические функции, зависящие от
угла.
Определяют тригонометрические функци
и обычно как отношения сторон
прямоугольного треугольника или длины
определённых отрезков в единичной
окружности. К тригонометрическим
функциям относятся функции:
y = sin x;
y = cos x;
y = tg x;
y = ctg x;
y = sec x;
y = cosec x.
14.
Обра́тные тригонометри́ческиефу́нкции — математические
функции, являющиеся обратными к
тригонометрическим функциям.
15.
Обратныетригонометрические функции
у=arcctgx
у=arcsinx
график
график
у=arccosx
график
у=arctgx
график
16. Сведения из истории
Современные обозначения arcsin иarctg появляются в 1772г.в работах
венского математика Щерфера и
известного французского ученого
Ж.Л. Лагранжа, хотя
несколько ранее уже
рассматривал Д. Бернулли,
который употреблял иную
символику.
17. Сведения из истории
• Общепринятыми эти символыстали лишь в конце XVIII
столетия. Приставка «арк»
происходит от латинского
arcus (лук, дуга), что вполне
согласуется со смыслом
понятия; arcsin х,
например,— это угол (а можно сказать, и
дуга),синус которого равен х.
18.
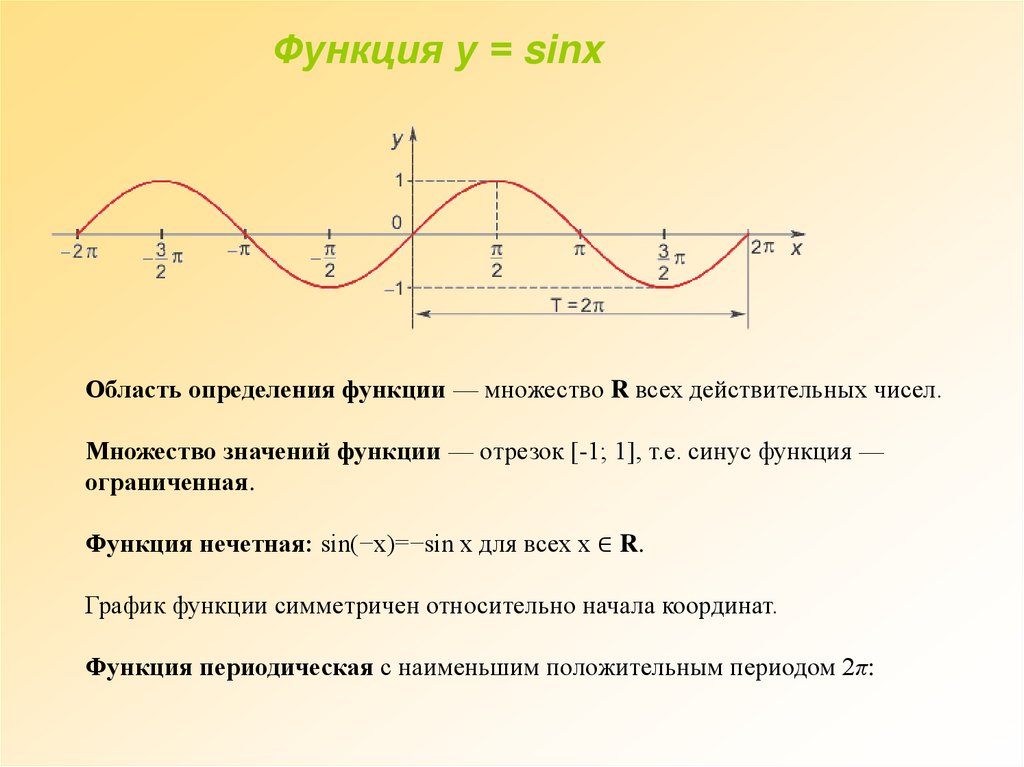
Функция у = sinxОбласть определения функции — множество R всех действительных чисел.
Множество значений функции — отрезок [-1; 1], т.е. синус функция —
ограниченная.
Функция нечетная: sin(−x)=−sin x для всех х ∈ R.
График функции симметричен относительно начала координат.
Функция периодическая с наименьшим положительным периодом 2π:
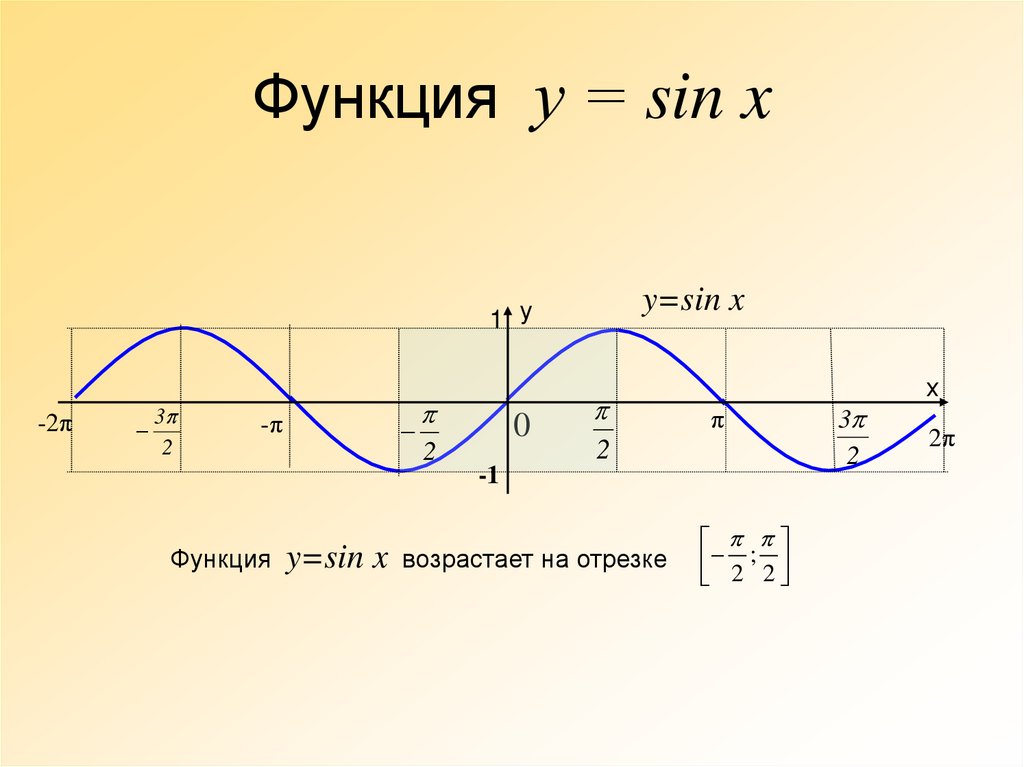
19. Функция у = sin x
y=sin x1 у
-2π
3
2
-π
Функция
y=sin x
2
0
2
π
-1
возрастает на отрезке
2 ; 2
3
2
х
2π
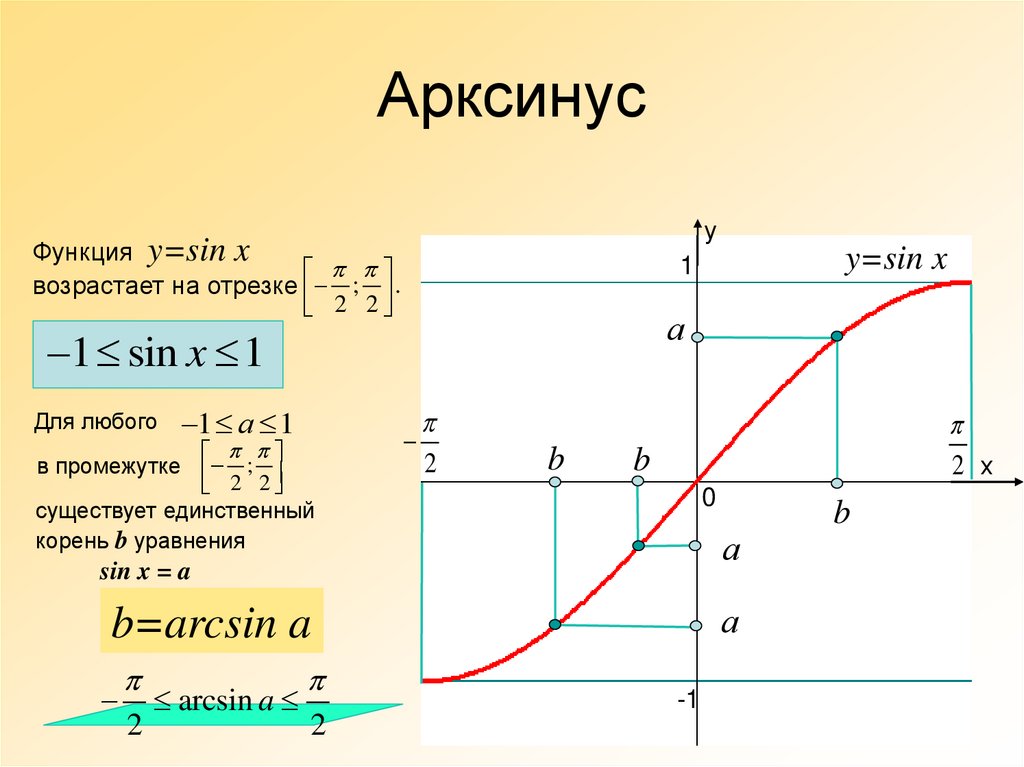
20. Арксинус
уФункция y=sin x
возрастает на отрезке ; .
2 2
а
1 sin x 1
Для любого
1 а 1
в промежутке ;
2 2
существует единственный
корень b уравнения
2
b
2 х
b
0
а
sin x = a
а
b=arcsin a
2
arcsin a
2
y=sin x
1
-1
b
21. Арксинус
Обозначение. Арксинус а обозначаетсяarcsina.
• Арксинусом числа а называется такое
число
из отрезка
, синус которого равен а.
Очевидно, что а є [-1;1].
Т.к
Функция y=arcsin x- нечетная,
поэтому
22.
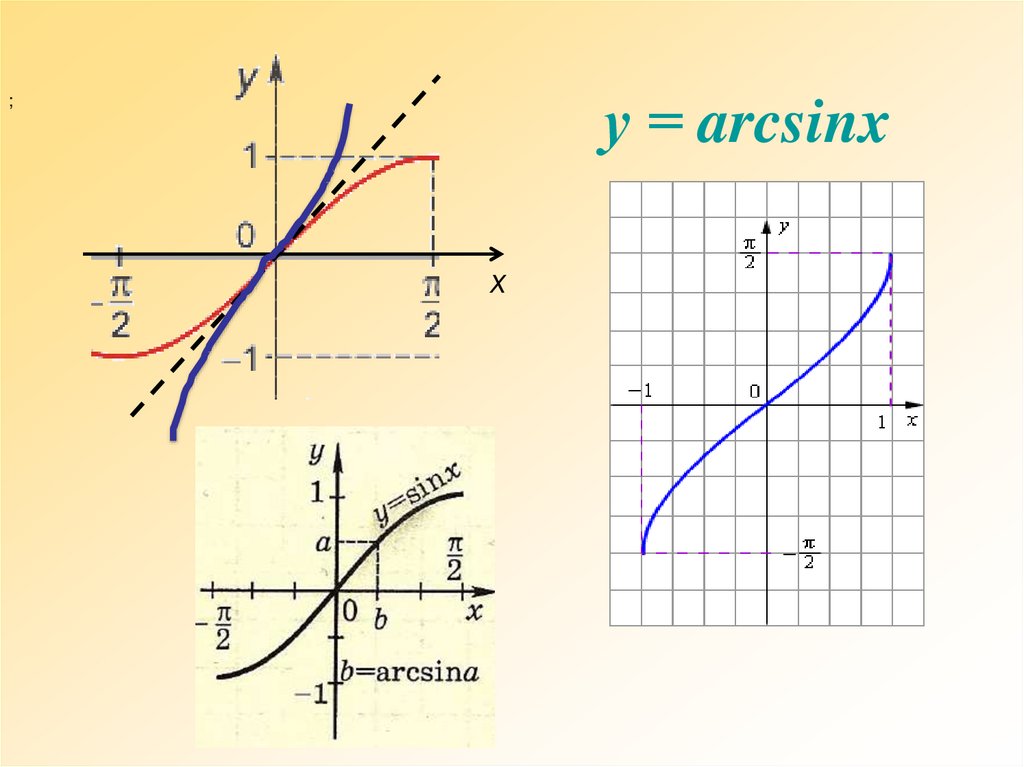
у = arcsinx;
х
23.
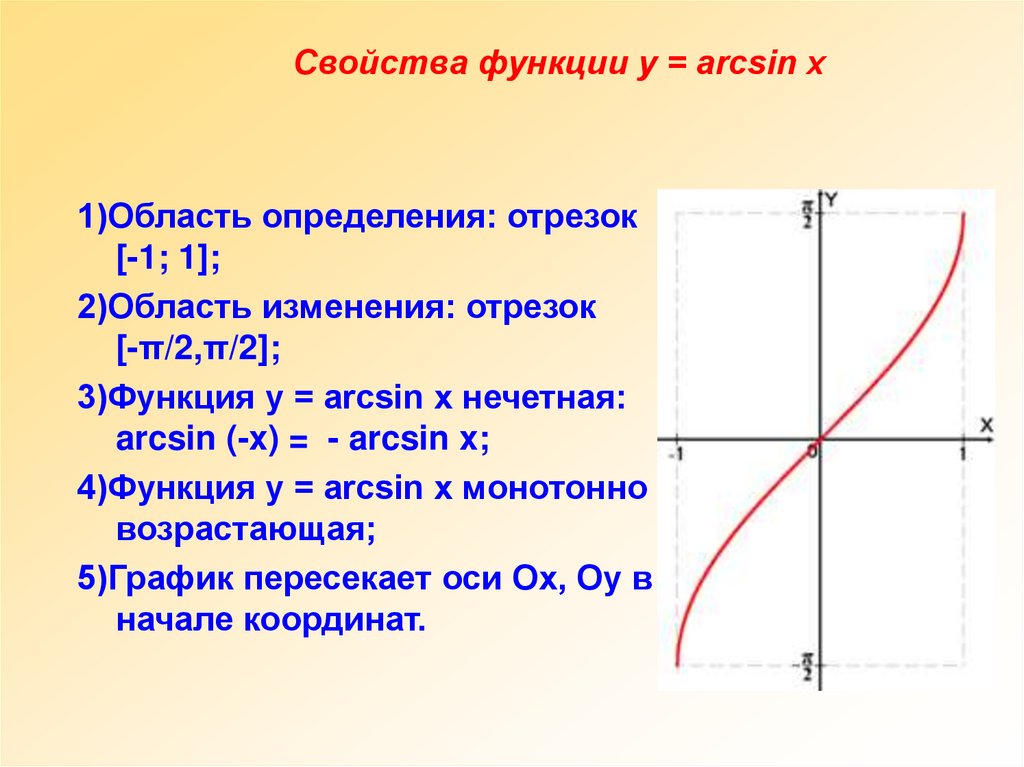
Свойства функции y = arcsin x1)Область определения: отрезок
[-1; 1];
2)Область изменения: отрезок
[-π/2,π/2];
3)Функция y = arcsin x нечетная:
arcsin (-x) = - arcsin x;
4)Функция y = arcsin x монотонно
возрастающая;
5)График пересекает оси Ох, Оу в
начале координат.
24.
2Определение
0
arcsin t = a
1)
2
2
2) sin t
3) 1 t 1
2
arcsin(-x) = - arcsinx
25. Примеры вычислений
sin
,так как
0, так как
=
, так как
26.
Функция у = cosxОбласть определения функции — множество R всех действительных чисел.
Множество значений функции — отрезок [-1; 1], т.е. косинус функция —
ограниченная.
Функция четная: cos(−x)=cos x для всех х ∈ R.
График функции симметричен относительно оси OY.
Функция периодическая с наименьшим положительным периодом 2π:
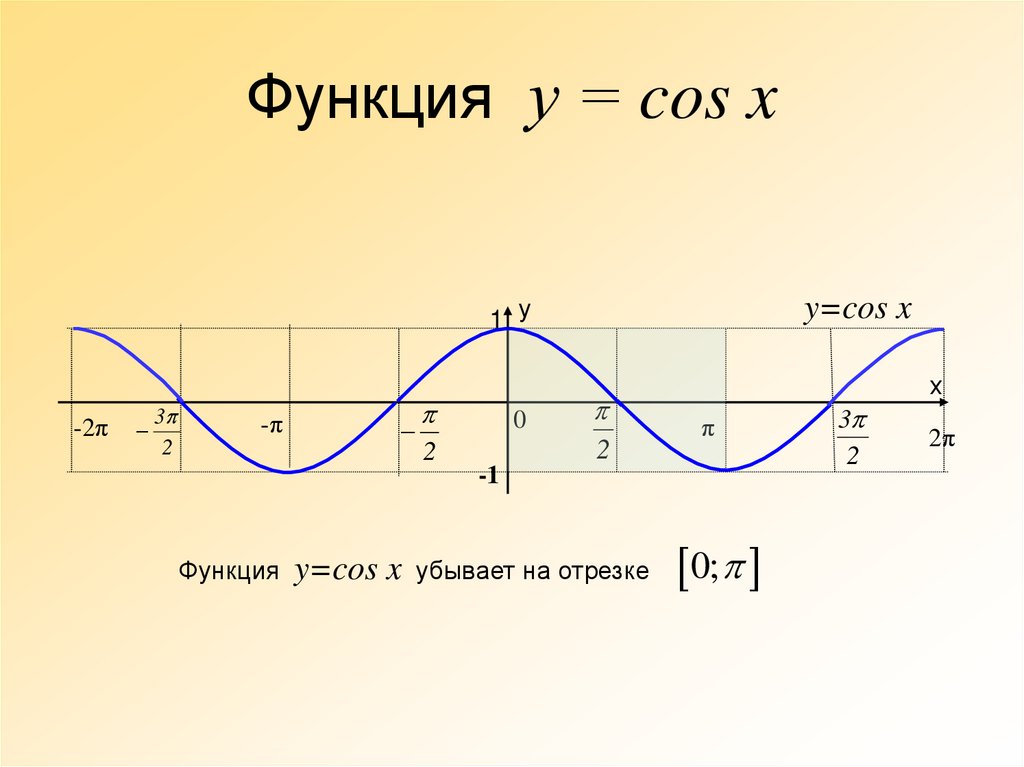
27. Функция у = cos x
1 у-2π
3
2
-π
Функция
y=cos x
2
0
y=cos x
2
х
π
-1
убывает на отрезке
0;
3
2
2π
28. Арккосинус
уФункция y=cos x
убывает на отрезке
0; .
1 cos x 1
1 а 1
в промежутке
0;
1
y=cos x
а
Для любого
существует единственный
корень b уравнения
cos x = a
b=arccos a
0 arccos a
b
0
а
а
-1
b
2
b
х
29. Арккосинус
Обозначение: Арккосинус а обозначаетсяarccosa.
• Арккосинусом числа а называется такое
число из отрезка
, косинус которого
равен а.
Очевидно, что а є [-1; 1]
• Т.к.
Функция y=arccosx- четная,
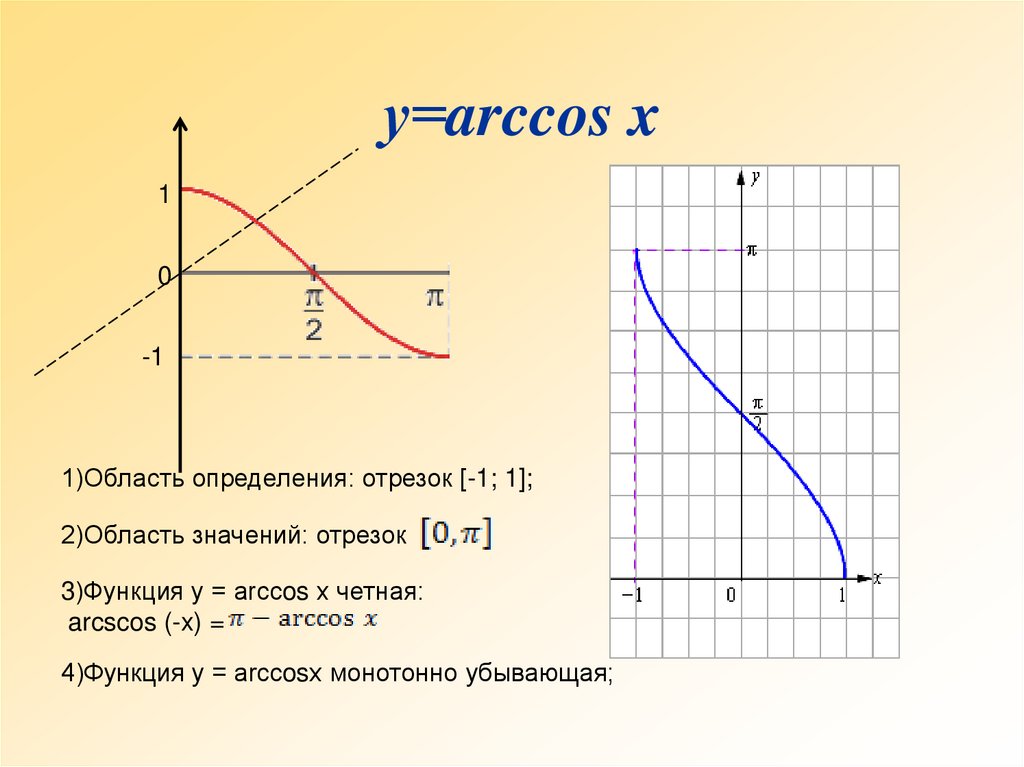
30.
у=arccos x1
0
-1
1)Область определения: отрезок [-1; 1];
2)Область значений: отрезок
3)Функция у = arcсos x четная:
arcscos (-x) =
4)Функция у = arcсosx монотонно убывающая;
31.
Свойства функции y = arccos x .1)Область определения: отрезок [-1; 1];
2)Область изменения:отрезок[0;π]
3)Функция y =
arccosx четная:
arccos(-x )=
arccosx
4)Функция y = arccos x
монотонно убывающая
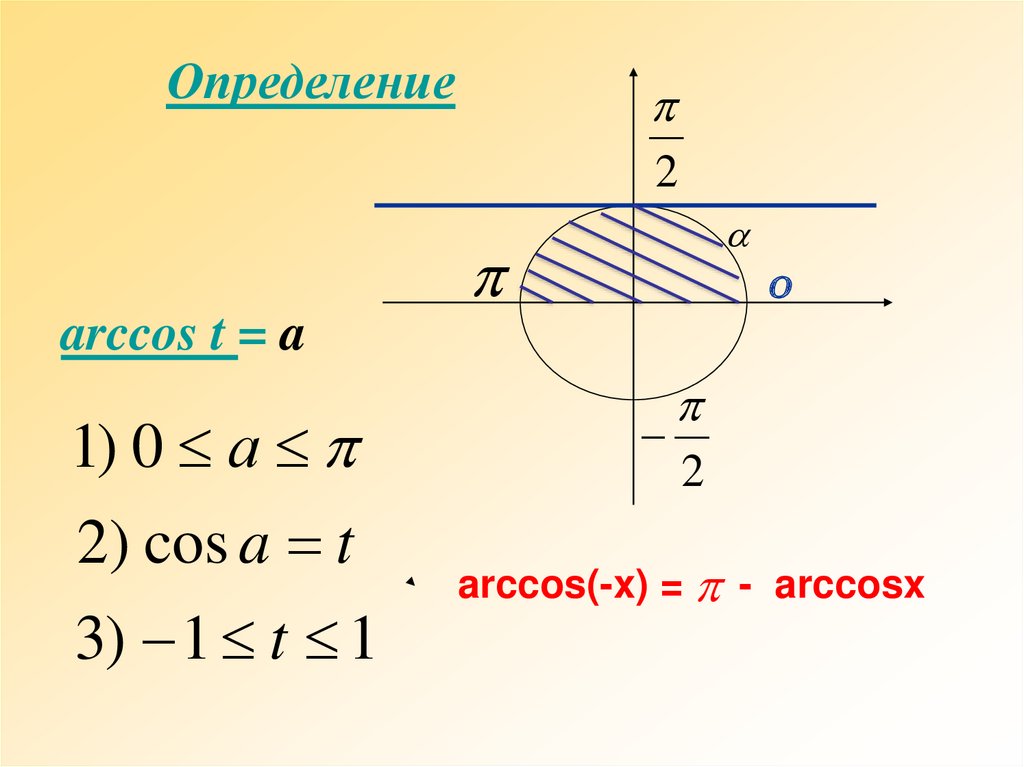
32.
Определение2
0
arccos t = a
1) 0 а
2) cos a t
3) 1 t 1
2
arccos(-x) = - arccosx
33. Примеры вычислений
• 1)• 2)
• 3)
• 4)
34.
Работаем устноarcsin 1
arcsin 0
arccos 1
arccos 0
2
arcsin
2
1
arcsin
2
1
arccos
2
1
arccos
3
arcsin(-x) = - arcsinx
1
arcsin( )
2
1
arccos( )
2
3
2
arcsin( )
arccos(
)
2
2
arccos(-x) = - arccosx
35.
Работаем устноИмеет ли смысл выражение?
arcsin 2 arccos 3
arctg100
Может ли arcsint и arccost принимать
значение равное
5
5, , , 10,
9
3
,?
7
36.
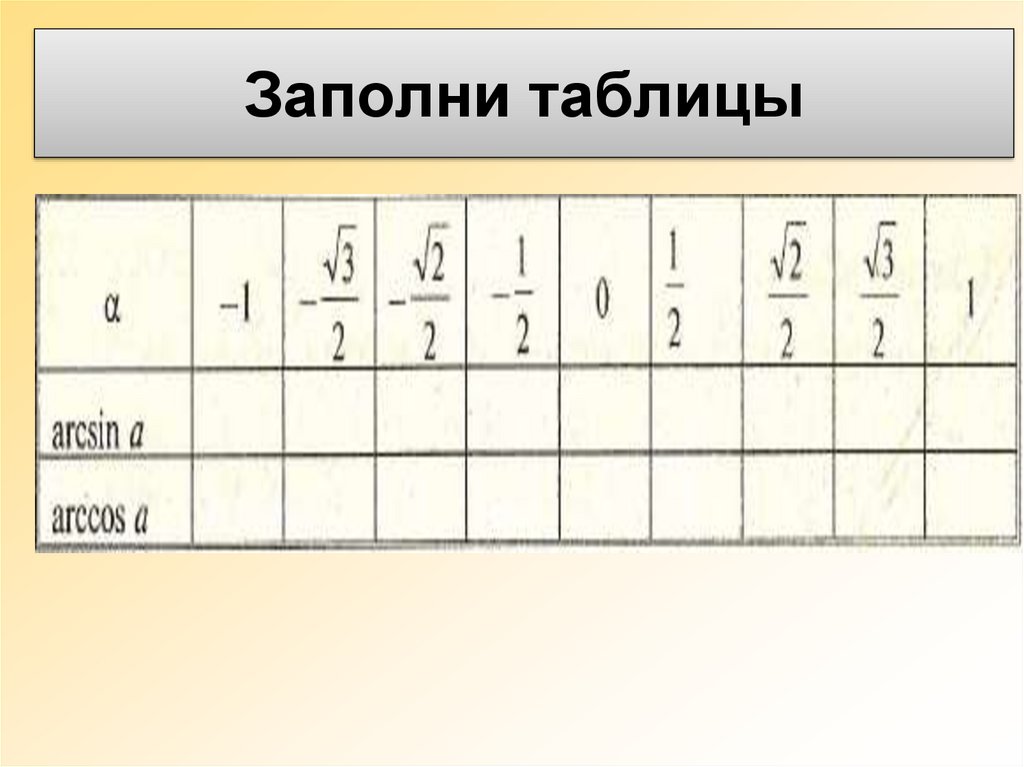
37. Заполни таблицы
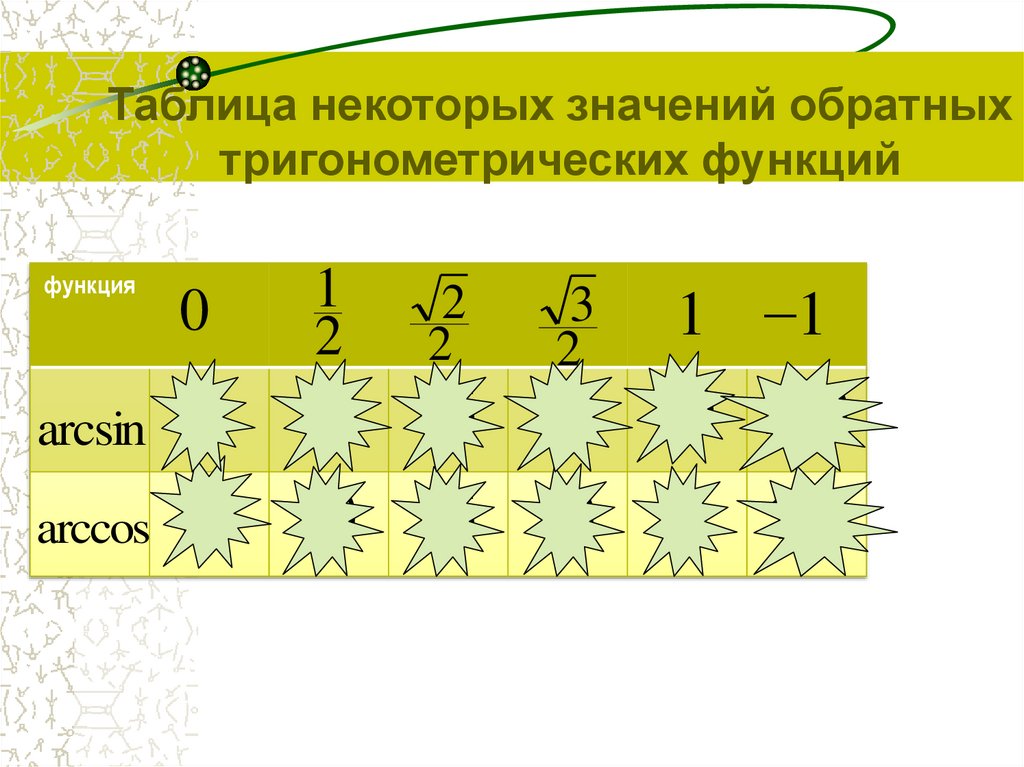
38.
Таблица некоторых значений обратныхтригонометрических функций
функция
arcsin
arccos
0
1
2
0
30 45 60 90 270
2
2
3
2
90 60 45 30
1 1
0 180



























 Математика
Математика








