Параллельность прямых. Прямой и плоскости

1.

Параллельность
прямых. Прямой и
плоскости.

2.

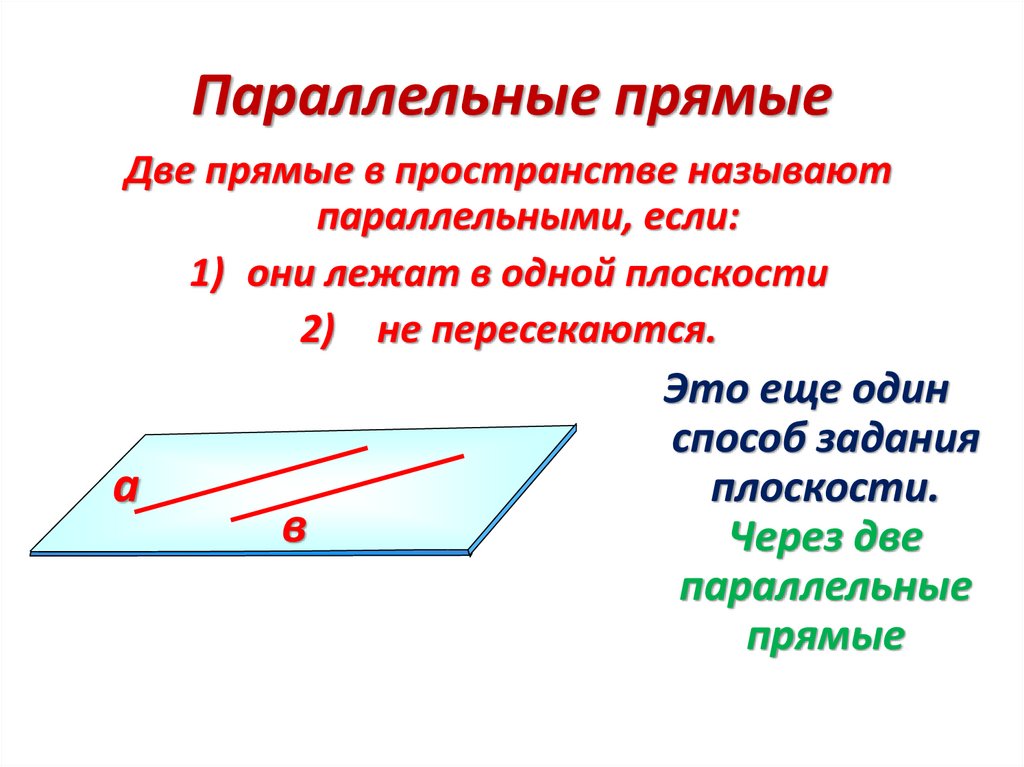
Параллельные прямые
Две прямые в пространстве называют
параллельными, если:
1) они лежат в одной плоскости
2) не пересекаются.
а
в
Это еще один
способ задания
плоскости.
Через две
параллельные
прямые

3.

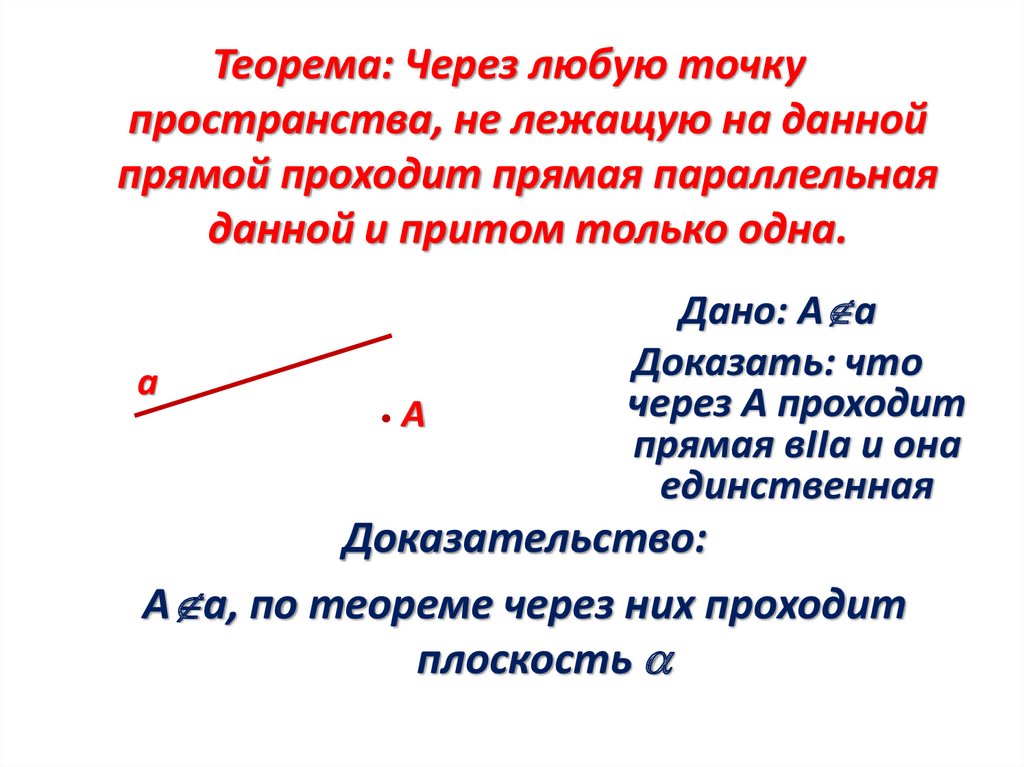
Теорема: Через любую точку
пространства, не лежащую на данной
прямой проходит прямая параллельная
данной и притом только одна.
а
А
Дано: А а
Доказать: что
через А проходит
прямая вIIа и она
единственная
Доказательство:
А а, по теореме через них проходит
плоскость

4.

а
в
А
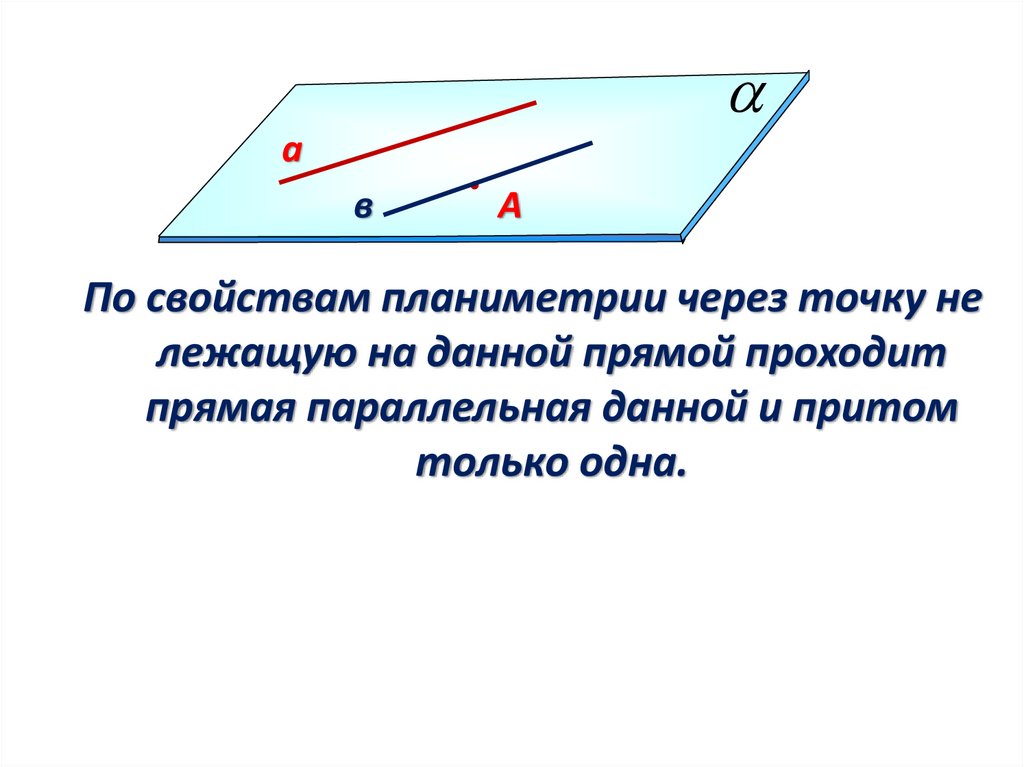
По свойствам планиметрии через точку не
лежащую на данной прямой проходит
прямая параллельная данной и притом
только одна.

5.

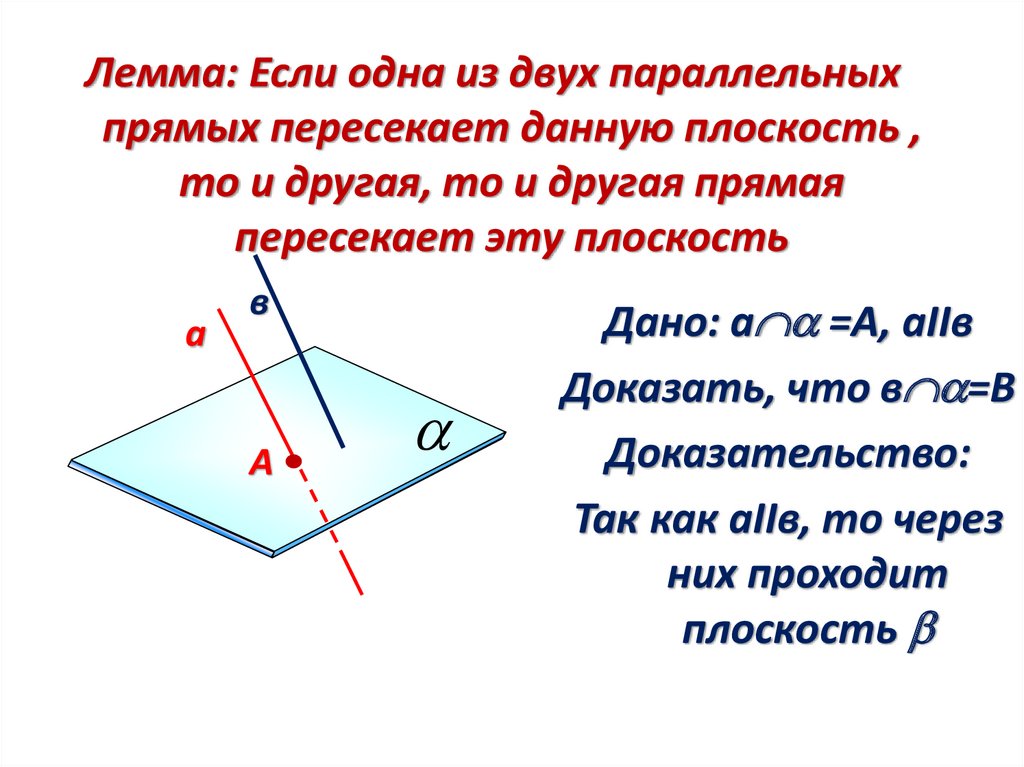
Лемма: Если одна из двух параллельных
прямых пересекает данную плоскость ,
то и другая, то и другая прямая
пересекает эту плоскость
а
в
А
Дано: а =А, аIIв
Доказать, что в =В
Доказательство:
Так как аIIв, то через
них проходит
плоскость

6.

а в
А
В m
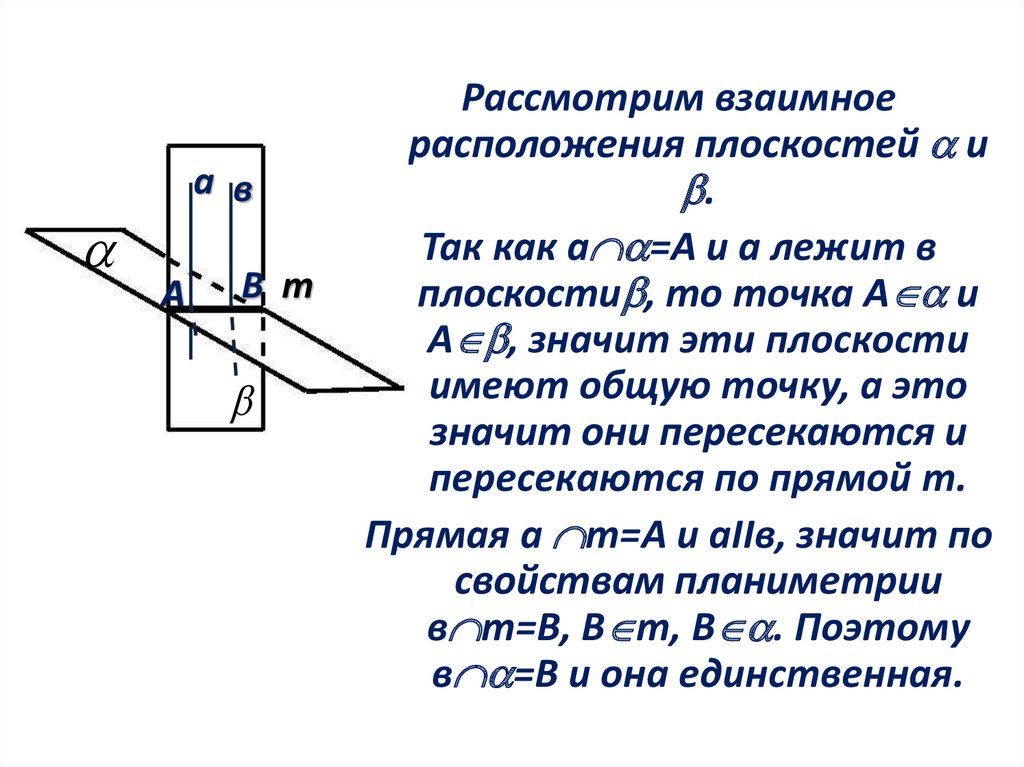
Рассмотрим взаимное
расположения плоскостей и
.
Так как а =А и а лежит в
плоскости , то точка А и
А , значит эти плоскости
имеют общую точку, а это
значит они пересекаются и
пересекаются по прямой m.
Прямая а m=А и аIIв, значит по
свойствам планиметрии
в m=В, В m, В . Поэтому
в =В и она единственная.

7.

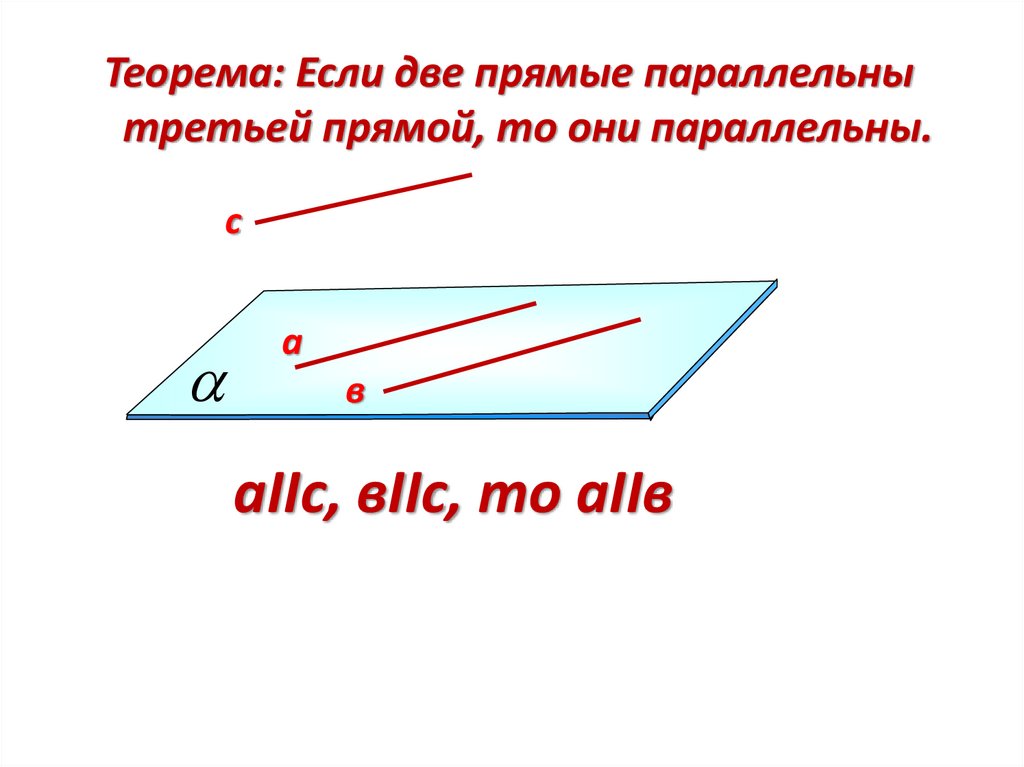
Теорема: Если две прямые параллельны
третьей прямой, то они параллельны.
с
а
в
аIIс, вIIс, то аIIв

8.

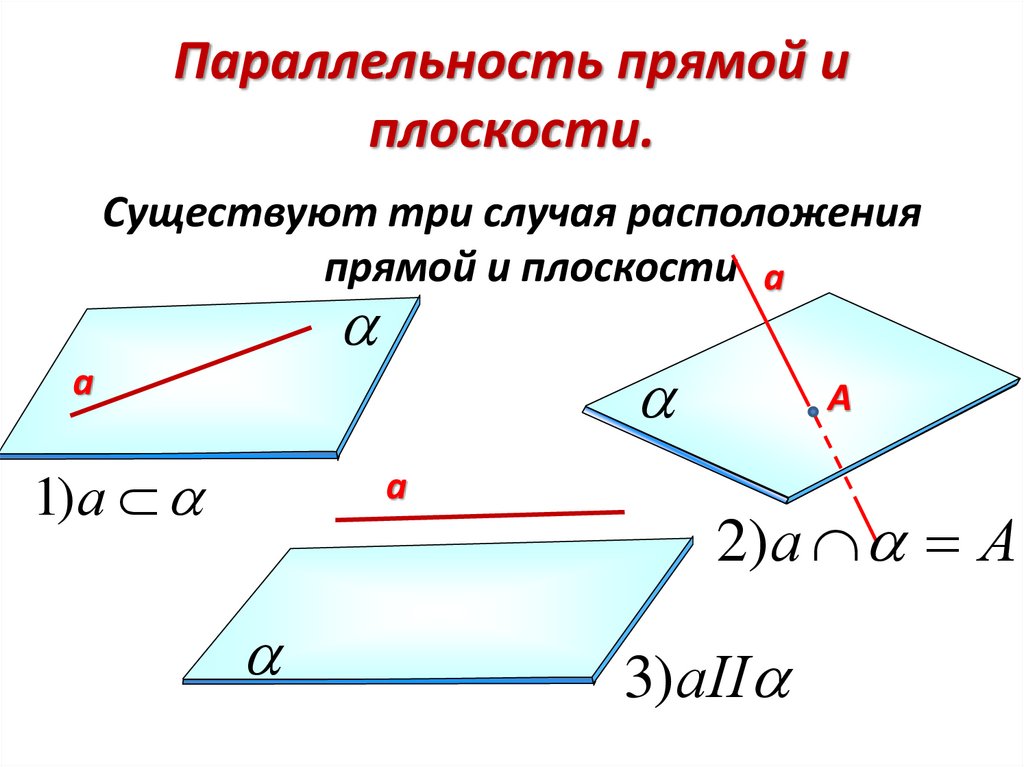
Параллельность прямой и
плоскости.
Существуют три случая расположения
прямой и плоскости а
а
1)а
а
А
2)а А
3)аII

9.

Прямая и плоскость называются
параллельными, если они не имеют
общих точек
Теорема.(Признак параллельности прямой и
плоскости)
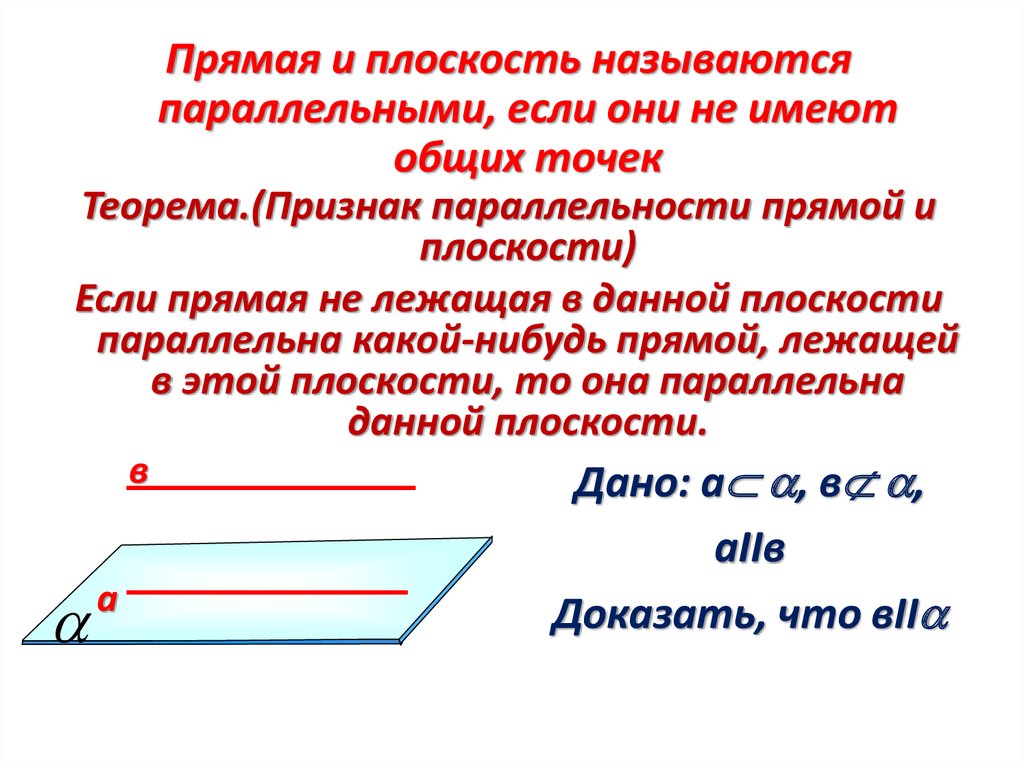
Если прямая не лежащая в данной плоскости
параллельна какой-нибудь прямой, лежащей
в этой плоскости, то она параллельна
данной плоскости.
в
а
Дано: а , в ,
аIIв
Доказать, что вII

10.

в
а
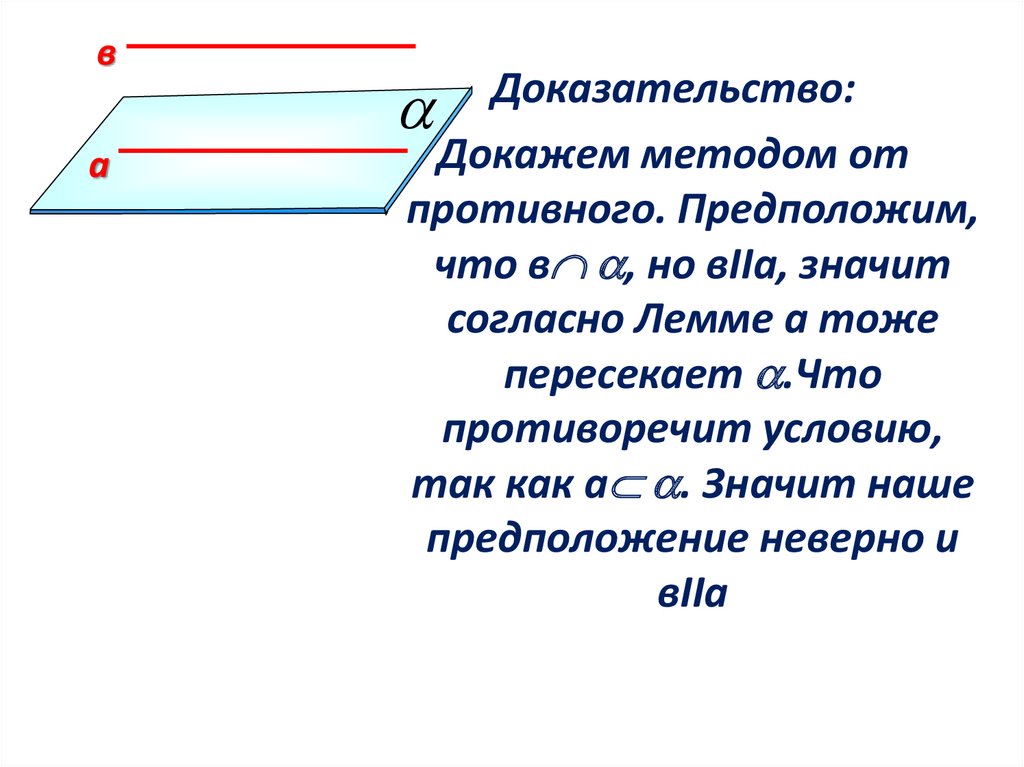
Доказательство:
Докажем методом от
противного. Предположим,
что в , но вIIа, значит
согласно Лемме а тоже
пересекает .Что
противоречит условию,
так как а . Значит наше
предположение неверно и
вIIа

11.

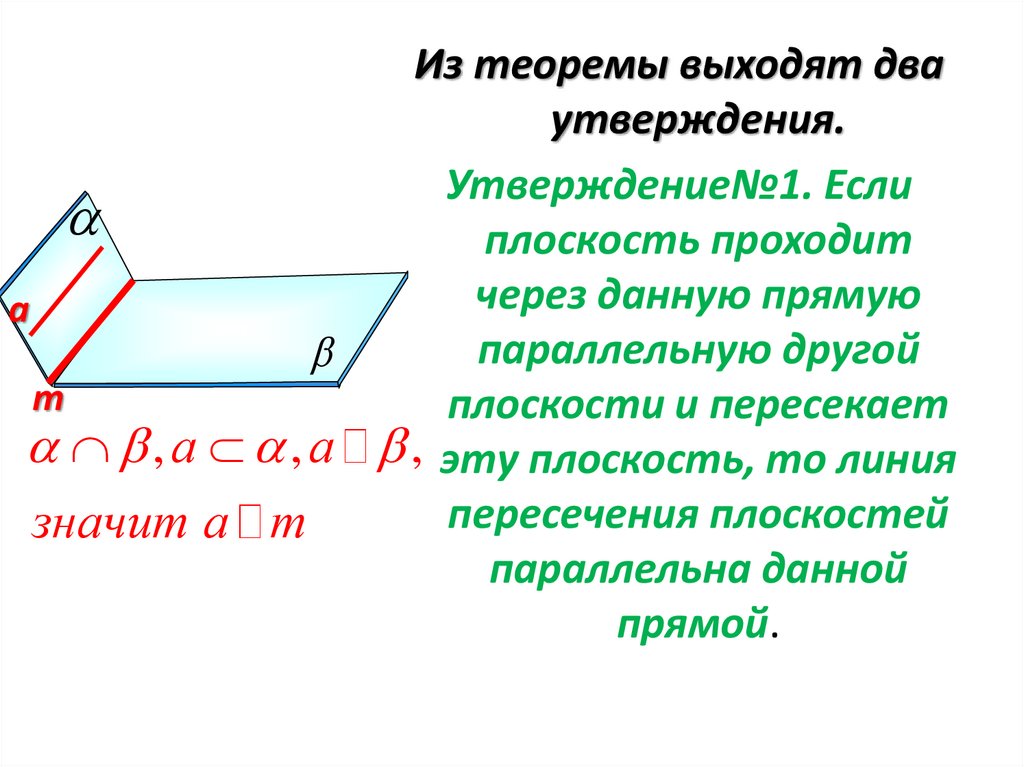
Из теоремы выходят два
утверждения.
Утверждение№1. Если
плоскость проходит
через данную прямую
а
параллельную другой
m
плоскости и пересекает
, а , а , эту плоскость, то линия
пересечения плоскостей
значит а m
параллельна данной
прямой.

12.

в
а
а
в
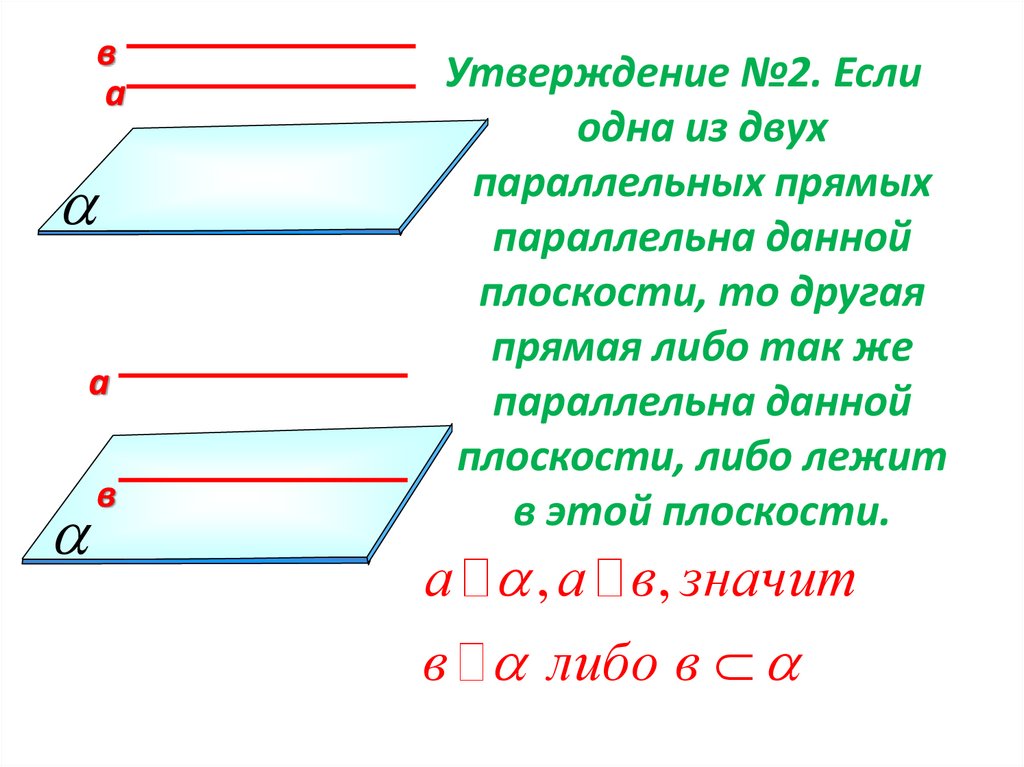
Утверждение №2. Если
одна из двух
параллельных прямых
параллельна данной
плоскости, то другая
прямая либо так же
параллельна данной
плоскости, либо лежит
в этой плоскости.
а , а в, значит
в либо в