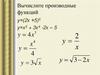Похожие презентации:
Применение производной для отыскания наибольших и наименьших величин
1.
Применение производной дляотыскания наибольших и
наименьших величин.
mathvideourok.moy.su
2.
1.Отыскание наибольшего инаименьшего значений непрерывной
функции на промежутке.
Аналитически:
Найти наименьшее и наибольшее
значения функции у 9 х 2
Решение :
Так как
9 х 0, то
2
унаим 0, унаиб 3
3.
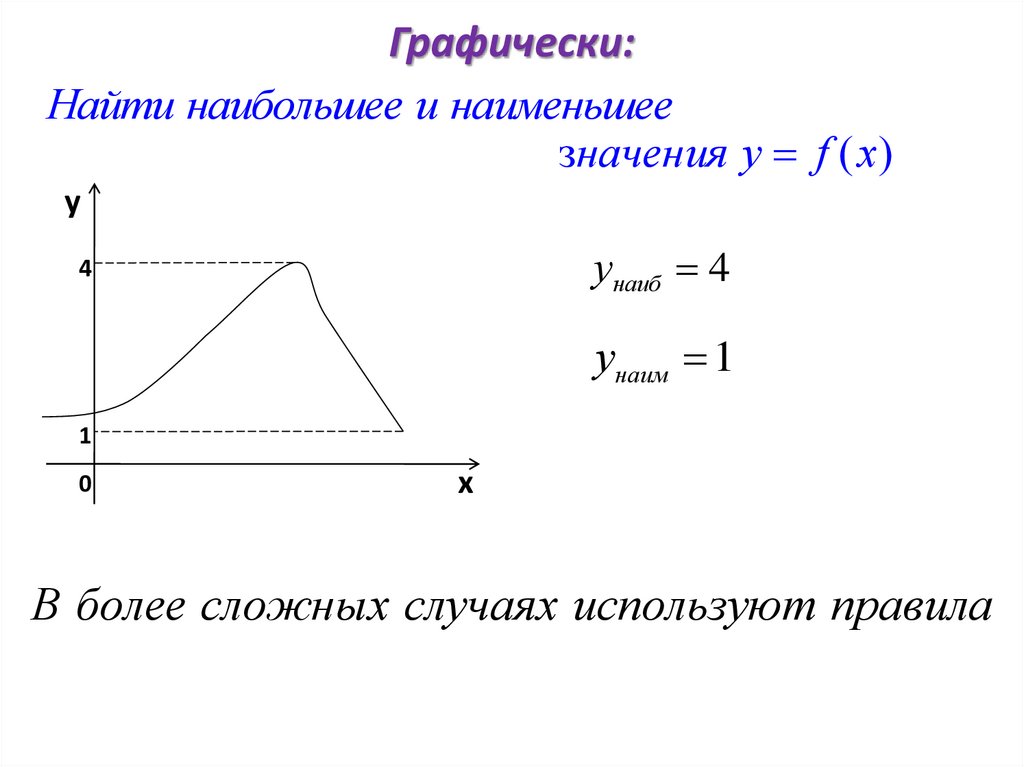
Графически:Найти наибольшее и наименьшее
значения у f ( x)
y
унаиб 4
4
унаим 1
1
0
х
В более сложных случаях используют правила
4.
*Если функция непрерывна на отрезке, тоона достигает на нем и своего
наименьшего и наибольшего значения.
*Наибольшего и наименьшего значения
непрерывная функция может достигать
как на концах отрезка, так и внутри
него.
*Если наибольшее (или наименьшее)
значение достигается внутри отрезка, то
только в стационарной или критической
точке.
5.
Алгоритм отыскания наименьшего инаибольшего значений непрерывной
функции на отрезке
y f ( x)на а; в
1.Найти D( f ) и f ( x)
2.Найти стационарные и критические точки
фукции лежащие внутри отрезка.
3.Вычислить значения функции y f ( x )
в точках а и в, а также в
стационарных и критических
4.Выбрать среди них наибольшее
и наименьшее
6.
1.Найти наименьшее и наибольшее значение функцииу х 3 3х 2 45 х 1 на 4;6
1) Д ( у ) R
Решение :
2) у 3х 6 х 45
3 х 2 6 х 45 0
х1 5; х2 3
2
5 4;6
-3 4;6
у (-4) 69
у (6) -161
у (5) -174
у (-3) 82
Ответ : унаим 174; унаиб 82
7.
Для отыскания наибольшего и наименьшего значенийфункции на промежутке применяют следующую
теорему
Теорема:
Пусть функция у f ( x) непрерывна на промежутке Х
и имеет внутри него стационарную или критическую точку
х х0 , тогда
1)если х х0 т.максимум, то унаиб f ( x0 )
2)если х х0 т.минимум, то унаим f ( x0 )
8.
2.Найти наибольшее значение функциих
у
на 0; )
2
1 х
Решение :
1) Д ( у ) R
1 х2
2) у
2 2
(1 х )
1 х
0
2 2
(1 х )
х 1 1 0; )
2
-1 0; )
y
y
0
y (0,5) 0
x
1
y (2) 0
xmax 1
y (1) 0,5 наиб.знач.
Ответ : унаиб 0,5
9.
2. Задачи на отыскание наибольшего инаименьшего значений величин.
Задачи на оптимизацию-это задачи на
нахождение наибольшего или
наименьшего значений какой-либо
величины.
10.
Алгоритм решения задач методомматематического моделирования
1.Задача переводится на язык функций.
Для этого выбирается удобный
параметр х, через который
интересующую нас величину выражают,
как функцию f(x).
2.Средствами анализа ищется наибольшее
или наименьшее значение этой функции
на некотором промежутке.
3.Выясняется какой практический смысл
имеет полученный результат на языке
задачи.
11.
1.Число 12 представьте в виде суммы двухположительных слагаемых так, чтобы сумма
куба первого слагаемого и утроенного второго
слагаемого была наименьшей?
Пусть х первое слагаемое, тогда (12 х )
второе. Составим функцию
f ( x) x 3(12 x) x 3 x 36
D ( f ) R, x (0;12) Найдем наименьшее
значение функции
2
3
f ( x) 3x 3
3x 3 0
2
x 1
3
1 (0;12)
1 (0;12)
12.
ff
0
1
12
x
x 1 точка минимум
значит наименьшее значение при х 1
Первое слагаемое 1, а другое 12 1 11
Ответ :12 1 11
13.
2.Бак,имеющий вид прямоугольногопараллелепипеда с квадратным
основанием должен вмещать V литров
жидкости. При какой стороне основания
площадь поверхности бака(без крышки)
будет наименьший?
V известная величина
Пусть х сторона квадрата в основании.
14.
VТак как V AA1 x x, то АА1 2
x
С1
В1
Составляем функцию
А1
V
x2
Д1
S ( x) Sосн Sбок
С
В
x
А
x
Д
Sосн х 2 ;
V 4V
Sбок =4 х 2 =
x
x
4V
2
S ( x)
x , х (0, )
x
Найдем наименьшее значение этой
функции
15.
4VS
S ( x) 2 2 x
x
3
S 0
x
2V
4V
4V 2V
2V
2 2x 0
3
S ( V )
3 2 0
x
2
3
( V)
( V)
3
4V 2 x 0
x 2V
x 3 2V
3
4V 6V
2V
0
S ( 3V )
2
2
(3 V )
(3 V )
3
x 2V точка минимум
Значит S бака будет наименьшим, если
3
сторона основания равна
3
2V














 Математика
Математика