Нахождение наибольшего и наименьшего значения функции

1.

Нахождение
наибольшего и
наименьшего значения
функции
(при решении задач
прикладного
характера).

2.

«Недостаточно лишь понять
задачу, необходимо желание
решить ее. Без сильного
желания решить трудную
задачу невозможно, но при
наличии такового возможно.
Где есть желание, найдется
путь!»
Пойа Д.

3.

Алгоритм решения задач
Этапы
1. Найти f /(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
3. Вычислить
значения функции в
критических точках
и на концах отрезка.
4. Из вычисленных
значений выбрать
наименьшее или
наибольшее
Найдите наименьшее значение функции
y = x3 – 27x на отрезке [0; 4]
1) y / = 3x2 – 27
3
-3
2) y / = 3x2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
x = 3 [0; 4]
x = –3 [0; 4]
3) y(0) = 0
y(4) = 43– 27 4 = – 44
y(3) = 33– 27 3 = –54
В 11
- 5 4
3
10 х
х

4.

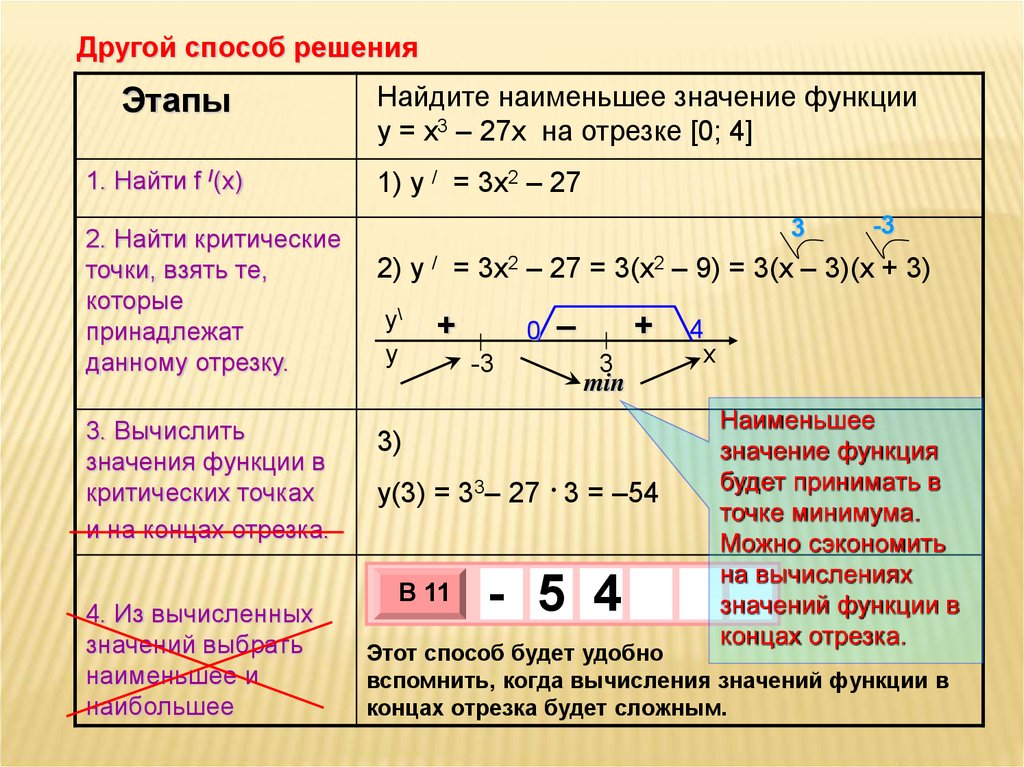
Другой способ решения
Этапы
1. Найти f /(x)
2. Найти критические
точки, взять те,
которые
принадлежат
данному отрезку.
3. Вычислить
значения функции в
критических точках
и на концах отрезка.
4. Из вычисленных
значений выбрать
наименьшее и
наибольшее
Найдите наименьшее значение функции
y = x3 – 27x на отрезке [0; 4]
1) y / = 3x2 – 27
3
-3
2) y / = 3x2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
y\
y
+
0
-3
–
+
3
min
4
x
3)
y(3) = 33– 27 3 = –54
В 11
- 5 4
3
10 х
х
Наименьшее
значение функция
будет принимать в
точке минимума.
Можно сэкономить
на вычислениях
значений функции в
концах отрезка.
Этот способ будет удобно
вспомнить, когда вычисления значений функции в
концах отрезка будет сложным.

5.

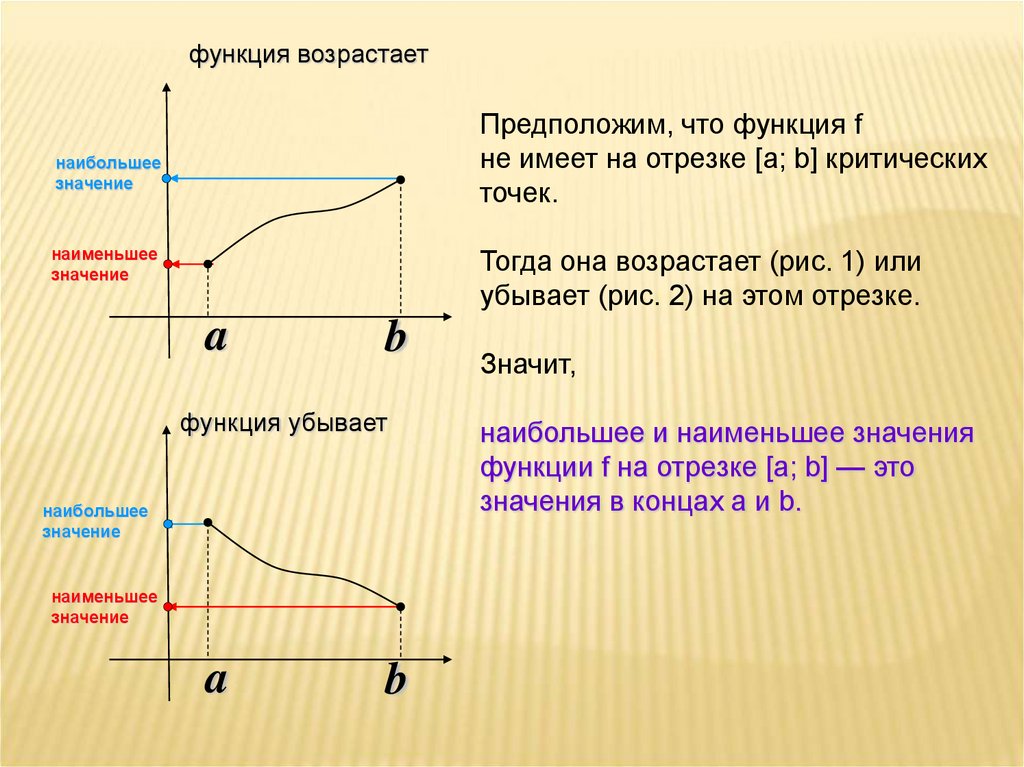
функция возрастает
Предположим, что функция f
не имеет на отрезке [а; b] критических
точек.
наибольшее
значение
наименьшее
значение
Тогда она возрастает (рис. 1) или
убывает (рис. 2) на этом отрезке.
a
b
функция убывает
наибольшее
значение
наименьшее
значение
a
b
Значит,
наибольшее и наименьшее значения
функции f на отрезке [а; b] — это
значения в концах а и b.

6.

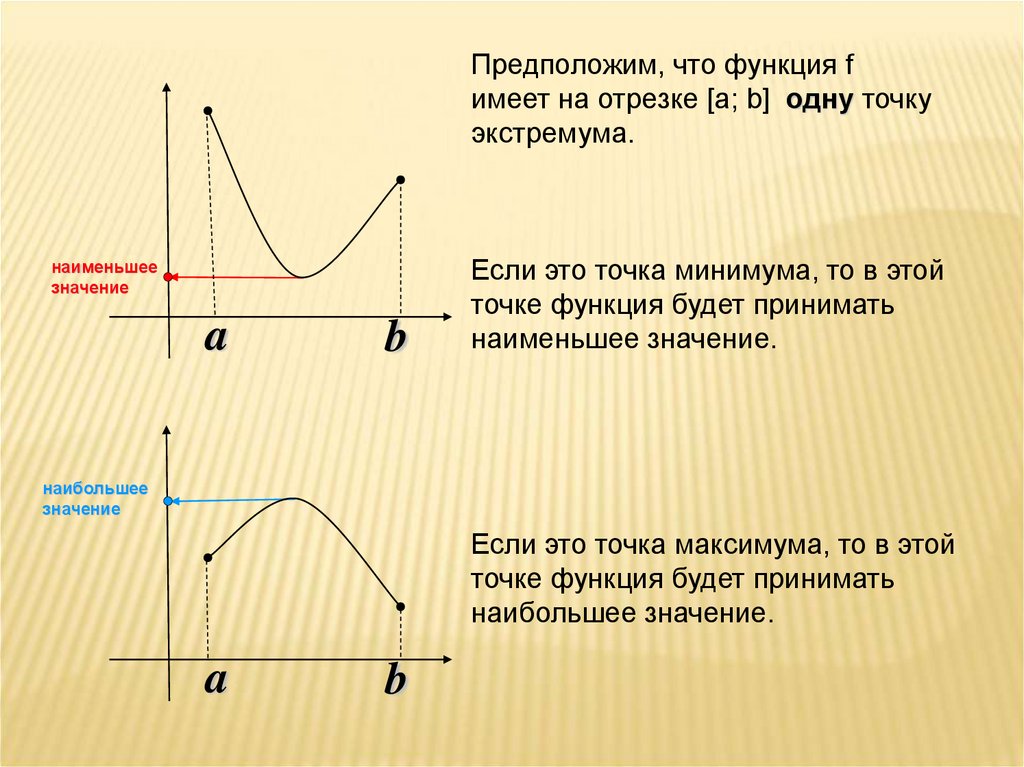
Предположим, что функция f
имеет на отрезке [а; b] одну точку
экстремума.
наименьшее
значение
a
b
Если это точка минимума, то в этой
точке функция будет принимать
наименьшее значение.
наибольшее
значение
Если это точка максимума, то в этой
точке функция будет принимать
наибольшее значение.
a
b

7. Рассказ «Много ли человеку земли нужно»

РАССКАЗ «МНОГО ЛИ ЧЕЛОВЕКУ ЗЕМЛИ
НУЖНО»
О крестьянине Пахоме, покупавшем землю у башкирцев.
-А цена какая будет?- говорит Пахом.
-Цена у нас одна: 1000 рублей за день.
Не понял Пахом.
-Какая же это мера – день? Сколько в ней десятин будет?
-Мы этого, - говорит, - не умеем считать. А мы за день продаем;
сколько обойдешь в день, то и твое, а цена 1000 рублей.
Удивился Пахом.
-Да ведь это, - говорит, -в день обойти земли много будет.
Засмеялся старшина.
-Вся твоя, - говорит. – Только один уговор: если назад не
придешь в день к тому месту, с какого возьмешься, пропали твои
деньги.
-А как же, - говорит, - отметить , где я пройду?
-А мы встанем на место, где ты облюбуешь; мы стоять будем, а
ты иди, делай круг, а с собой скребку возьми и, где надобно,
замечай, на углах ямки рой, дернички клади; потом с ямки на ямку
плугом пройдем. Какой хочешь круг забирай, только до захода
солнца приходи к тому месту, с какого взялся. Что обойдешь, все
твое.
Л.Н. Толстой

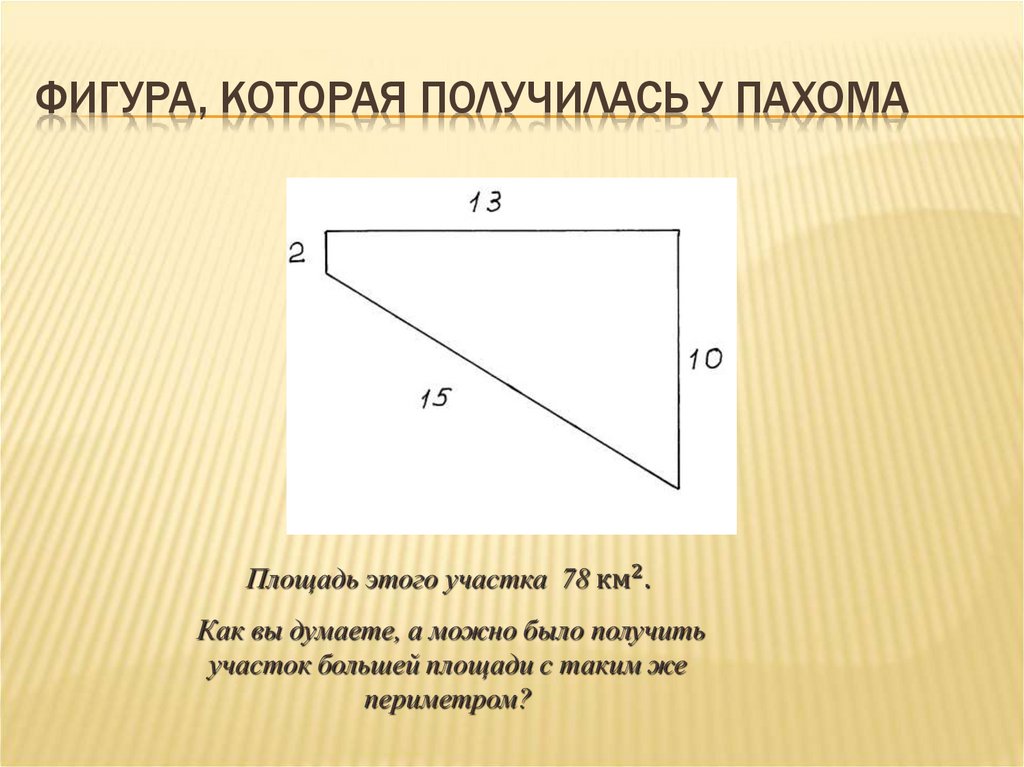
8. Фигура, которая получилась у Пахома

ФИГУРА, КОТОРАЯ ПОЛУЧИЛАСЬ У ПАХОМА

9. Задача 1

ЗАДАЧА 1
Периметр прямоугольника равен 40
км. Какую длину должны иметь
стороны прямоугольника, чтобы
площадь была наибольшей?

10. Задача 2:

ЗАДАЧА 2:
Выращенную на участке клубнику ученики
отправляют в детский сад в коробках,
имеющих форму прямоугольного
параллелепипеда с квадратным основанием,
периметр боковой грани которого 72 см.
Какими должны быть размеры коробки, чтобы
ее вместимость была наибольшей ?

11.

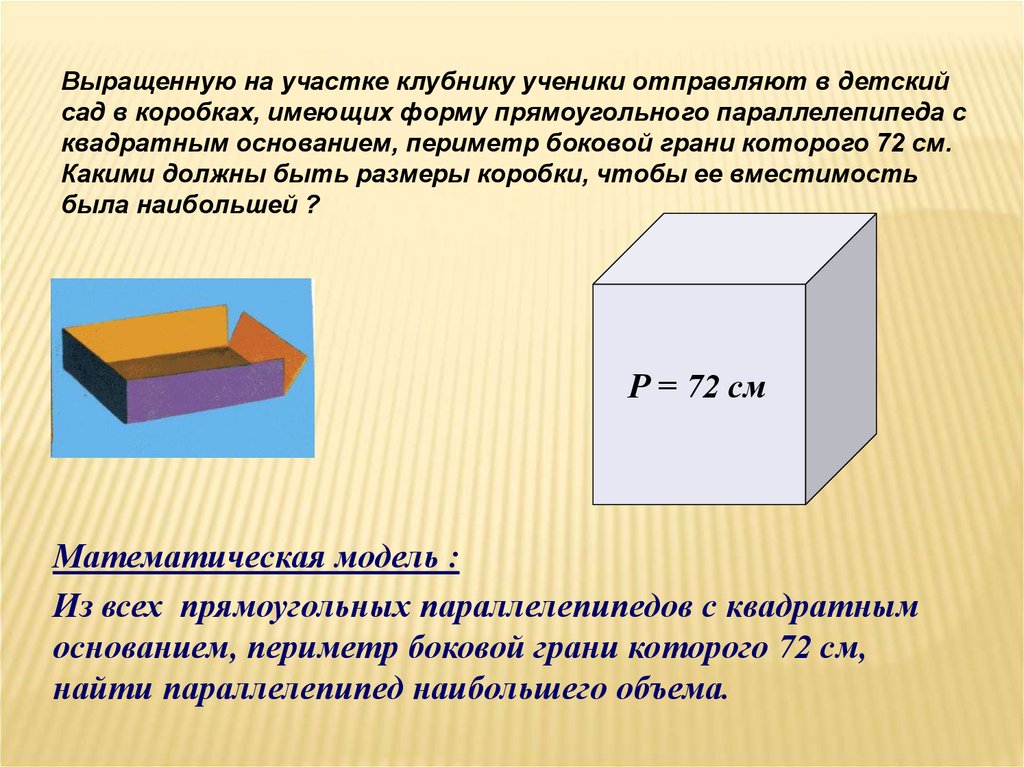
Выращенную на участке клубнику ученики отправляют в детский
сад в коробках, имеющих форму прямоугольного параллелепипеда с
квадратным основанием, периметр боковой грани которого 72 см.
Какими должны быть размеры коробки, чтобы ее вместимость
была наибольшей ?
Р = 72 см
Математическая модель :
Из всех прямоугольных параллелепипедов с квадратным
основанием, периметр боковой грани которого 72 см,
найти параллелепипед наибольшего объема.

12.

Из всех прямоугольных параллелепипедов с квадратным
основанием, периметр боковой грани которого 72 см,
найти параллелепипед наибольшего объема.
1. V – объем прямоугольного
параллелепипеда
2. х ( см ) – длина прямоугольного
параллелепипеда ,
х ( см ) – ширина прямоугольного
параллелепипеда
36 – х ( см ) – высота
прямоугольного параллелепипеда
x 0
3.
36 x 0
x 0
x 36 ,
36 – х
Р = 72 см
х
х
0 x 36
4. V x 2 ( 36 x )
V S основания h

13.

v( x )
5.
Рассмотрим функцию v ( x ) x 2 ( 36 x )
2
v ( x ) 72x 3x 3x ( 24 x )
v ( x ) 0 ,
x1 0 , x2 24
0 0 ; 36
v( x )
v ( x )
+
0
24
36
х
x = 24 – точка максимума, значит функция v ( х ) в этой точке
принимает наибольшее значение. Следовательно и объем
прямоугольного параллелепипеда при х = 24 будет наибольшим.

14.

Длина прямоугольного параллелепипеда – 24 ( см )
Ширина прямоугольного параллелепипеда – 24 ( см )
Высота прямоугольного параллелепипеда 36 – 24 = 12 ( см )
Ответ : чтобы вместимость коробки была наибольшей,
ее размеры должны быть 24 см, 24 см, 12 см

15. Алгоритм отыскания наибольшего и наименьшего значения

АЛГОРИТМ ОТЫСКАНИЯ НАИБОЛЬШЕГО И
НАИМЕНЬШЕГО ЗНАЧЕНИЯ
1. Выбирают независимую переменную и выражают
через неё ту величину, для которой находится
наибольшее и наименьшее значение, как функцию.
2. Находят промежуток изменения независимой
переменной.
3. Ищется наибольшее и наименьшее значение
функции на найденном промежутке.
4. Записывают ответ.

16.

Задача 3
Какими должны быть размеры участка
2
прямоугольной формы площадью 1600 м
,
чтобы на его ограждение было израсходовано
наименьшее количество материала ?
Составим математическую модель задачи :
из всех прямоугольников площадью 1600 кв. м
найти прямоугольник наименьшего
периметра

17. Из всех прямоугольников площадью 1600 кв. м найти прямоугольник наименьшего периметра.

ИЗ ВСЕХ ПРЯМОУГОЛЬНИКОВ ПЛОЩАДЬЮ 1600 КВ. М
НАЙТИ ПРЯМОУГОЛЬНИК НАИМЕНЬШЕГО ПЕРИМЕТРА.
1. Р – периметр прямоугольника
2. х ( м ) – длина прямоугольника
1600
( м ) ширина прямоугольника
х
x 0
3. 1600
0
x
;
x 0
S 1600 м
х
1600
4. P 2 x
x
5. Рассмотрим функцию
1600
р (x) 2 x
x
2
1600
х

18.

1600
3200
5. p (x) 2 x
2x
x
x
3200 2x 2 3200 2 ( x 2 1600 ) 2( x 40 ) ( x 40 )
p (x) 2 2
2
2
x
x
x
x2
p ( x ) 0,
x1 40 ,
40 0 ;
p ( х )
p( х )
0
x2 40
+
40
х
x = 40 – точка минимума, значит функция р ( х ) в этой точке
принимает наименьшее значение. Следовательно и периметр
прямоугольника будет наименьшим.

19.

Длина прямоугольника –
40 ( м )
Ширина прямоугольника –
1600
40 ( м )
40
Длина участка – 40 ( м )
Ширина участка – 40 м
Ответ:
длина участка 40 м, ширина участка – 40 м.

20.

Стоимость (за один час перевозки) содержания баржи
состоит из двух частей: стоимости топлива,
пропорциональной кубу скорости баржи, и стоимости
амортизации баржи ( зарплата команды, стоимость
оборудования и т. д.). Общая стоимость содержания
баржи за час выражается формулой: S = av³ + b, где vскорость судна в км/ч, a и b – коэффициенты,
заданные для каждого судна (для нашего а=0,005,
b=40).
Ясно, что расходы на топливо будут тем больше,
чем быстрее движется корабль, остальные расходы
от скорости не зависят.
Казалось бы, чем медленнее движется корабль, тем
дешевле его эксплуатация. Так ли это?

21. Вывод:

ВЫВОД:
Производная функции успешно
применяется при решении
оптимальных задач в
различных сферах
деятельности человека

22. Спасибо за урок!

СПАСИБО ЗА УРОК!