Похожие презентации:
Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке
1. ”Особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека:
какрасполагать своими
средствами для достижения
наибольшей выгоды”.
2. Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке
ТемаНахождение наибольшего и
наименьшего значений
непрерывной функции на
промежутке
3. ° ВЫВЕСТИ АЛГОРИТМ НАХОЖДЕНИЯ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЙ ФУНКЦИИ. ° РЕШАТЬ ЗАДАЧИ НА ОТЫСКАНИЕ НАИБОЛЬШИХ И НАИМЕНЬШИХ
Цели урока:° ВЫВЕСТИ АЛГОРИТМ НАХОЖДЕНИЯ
НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЙ
ФУНКЦИИ.
° РЕШАТЬ ЗАДАЧИ НА ОТЫСКАНИЕ
НАИБОЛЬШИХ И НАИМЕНЬШИХ ЗНАЧЕНИЙ
ФУНКЦИИ.
4.
yy
y
Y= f(x)
0 а
Y= f(x)
b x
0
а
Y= f(x)
b
x
0 а
b x
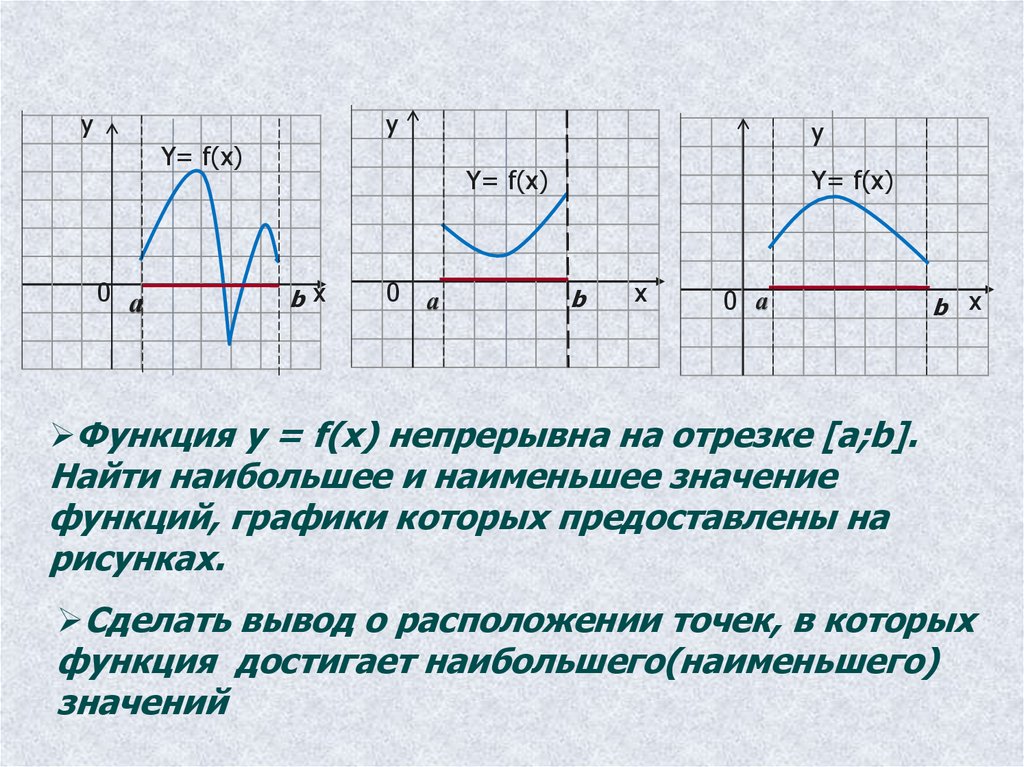
Функция у = f(х) непрерывна на отрезке [a;b].
Найти наибольшее и наименьшее значение
функций, графики которых предоставлены на
рисунках.
Сделать вывод о расположении точек, в которых
функция достигает наибольшего(наименьшего)
значений
5.
5. Назвать необходимые и достаточныеусловия существования точек
экстремума функции
6. а) если х = хо – точка максимума, то унаиб= f(xo)
Теорема.Пусть функция у = f(x) непрерывна на
промежутке Х и имеет внутри него единственную
стационарную или критическую точку х = хо.
y
Тогда:
Y= f(x)
а) если х = хо – точка максимума,
то унаиб= f(xo)
У
наиб.
0 а
хо
b
x
y
б) если х = хо – точка минимума,
то унаим= f(xo)
Y= f(x)
0 а
У наим.
хо
b
x
7. Алгоритм нахождения наибольшего и наименьшего значений непрерывной функции у = f(x) на отрезке [a;b]
1. Найти производную f´(х)2. Найти стационарные и критические точки
функции, лежащие внутри oтрезка [a;b]
3. Вычислить значение функции у= f(x) в точках,
отобранных на втором шаге, и в точках a и b.
Выбрать среди этих значений наименьшее
( это будет унаим )и наибольшее (это будет унаиб )
8.
у5
4
2
1
-7
-5
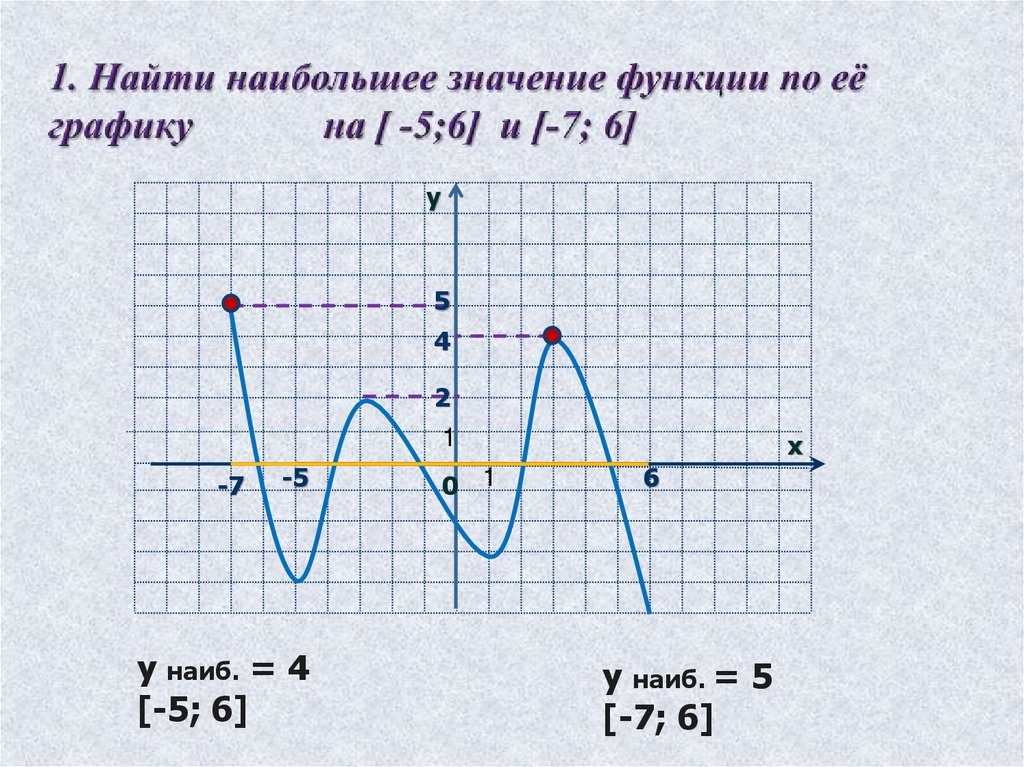
у наиб. = 4
[-5; 6]
0 1
х
6
у наиб. = 5
[-7; 6]
9.
у5
4
2
1
-7
-5
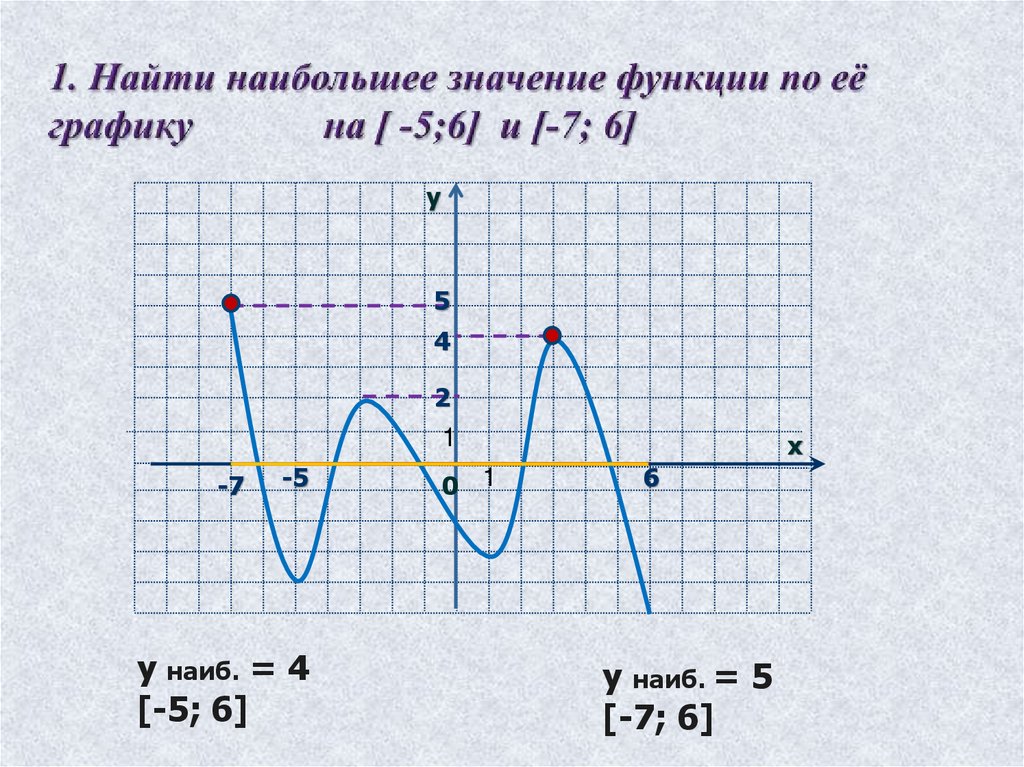
у наиб. = 4
[-5; 6]
0 1
х
6
у наиб. = 5
[-7; 6]
10.
у5
4
2
1
-7
-5
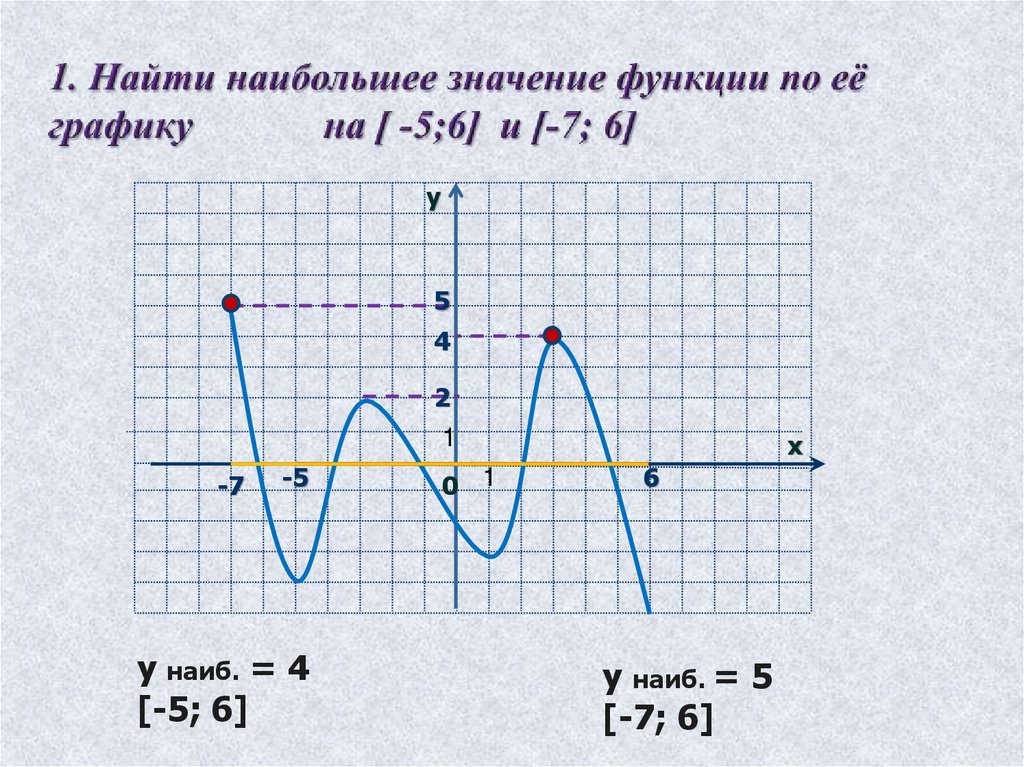
у наиб. = 4
[-5; 6]
0 1
х
6
у наиб. = 5
[-7; 6]
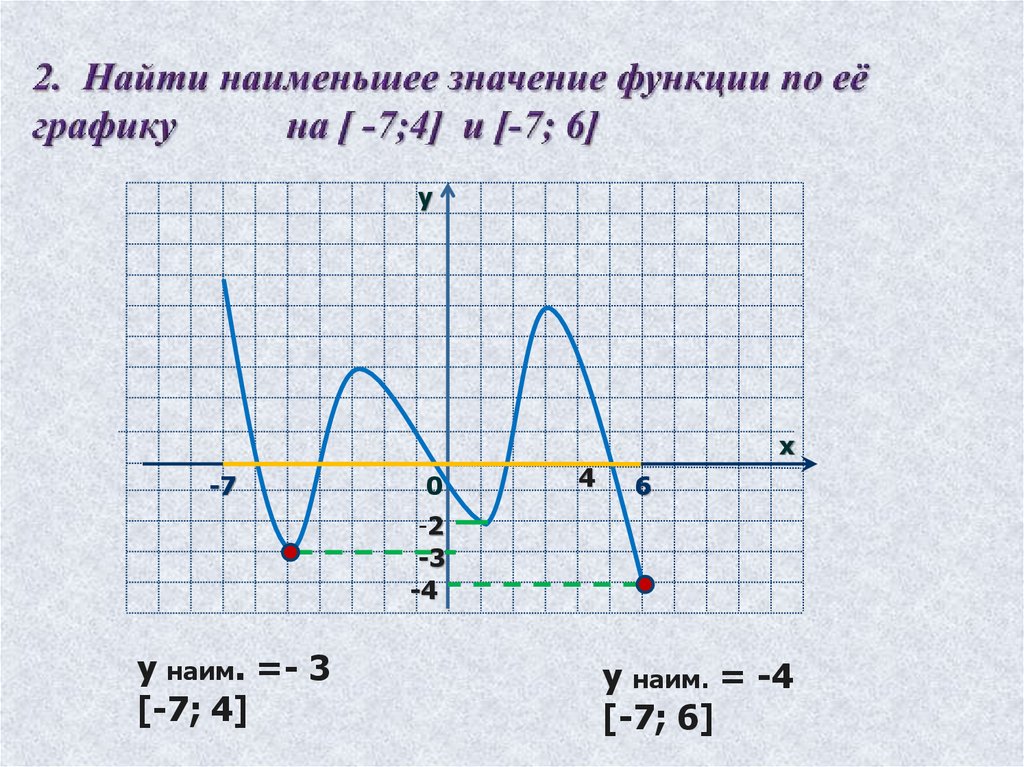
11.
ух
-7
0
4
6
-2
-3
-4
у наим. =- 3
[-7; 4]
у наим. = -4
[-7; 6]
12. Выводы
1.Если функция непрерывна на отрезке, то онадостигает на нем и своего наибольшего, и своего
наименьшего значений.
2.Наибольшего
и
наименьшего
значений
непрерывная функция может достигать как на
концах отрезка, так и внутри него.
3.Если наибольшее (или наименьшее) значение
достигается
внутри
отрезка,
то
только
в
стационарной или критической точке.
13.
Задание 1.Найти наибольшее и наименьшее значение
функции у = х³ - 3х² - 45х + 1 на [-4; 6]
без построения графика.
14.
Задание 2.Найти наибольшее и наименьшее значение
функции у = х³ - 5х² + 7х на [-1; 2]
без построения графика.
Ответ: : у наим = у (-1) = -13; у наиб = у(1) = 3
15. Нахождение наибольшего и наименьшего значений функции широко применяется при решении многих практических задач на нахождение
наилучших, оптимальных решенийпри наименьших затратах труда, в так
называемых
задачах
на
оптимизацию.
ПРИМЕР. Рекламный щит имеет форму
прямоугольника S=9 м2. Изготовьте щит в
виде прямоугольника с наименьшим
периметром





![Алгоритм нахождения наибольшего и наименьшего значений непрерывной функции у = f(x) на отрезке [a;b] Алгоритм нахождения наибольшего и наименьшего значений непрерывной функции у = f(x) на отрезке [a;b]](https://cf2.ppt-online.org/files2/slide/i/ibFG7CJUkgZwYKTvSz0ILpNyc23RDnMuQHehst/slide-6.jpg)




 Математика
Математика








