Атомное ядро. Центральная часть атома

1. Атомное ядро

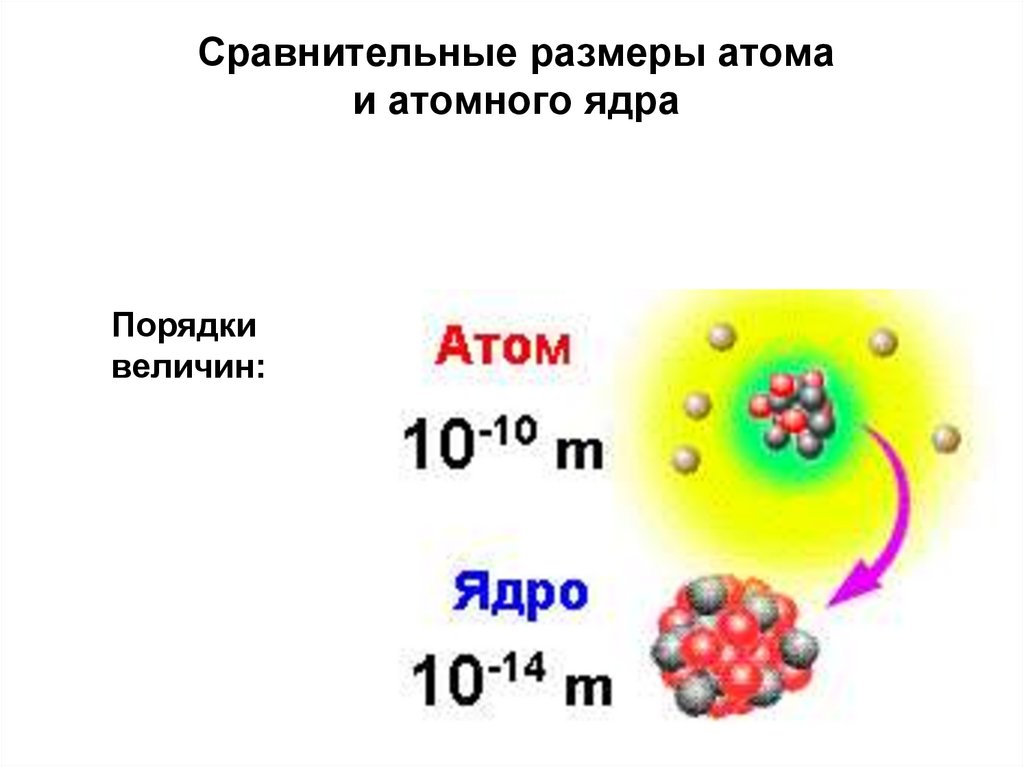
Центральная часть атома

2. Сравнительные размеры атома и атомного ядра

Порядки
величин:

3. Состав атомного ядра

Z протонов и N нейтронов,
где Z – порядковый номер химического элемента.
Протоны и нейтроны называются нуклонами, т.е.
внутриядерными частицами.

4. Нуклоны

Протон.
Электрический заряд: e = 4,8032 10–10 СГСЕ
(элементарный)
Масса: mp = 1,6726231 10–24 г
Спиновое квантовое число s = 1/2
Нейтрон.
Электрический заряд: 0
Масса: mn = 1, 6749286 10–24 г
Спиновое квантовое число s = 1/2
Массы нуклонов близки к атомной единице массы
1 а.е.м. 1,66 10–24 г

5.

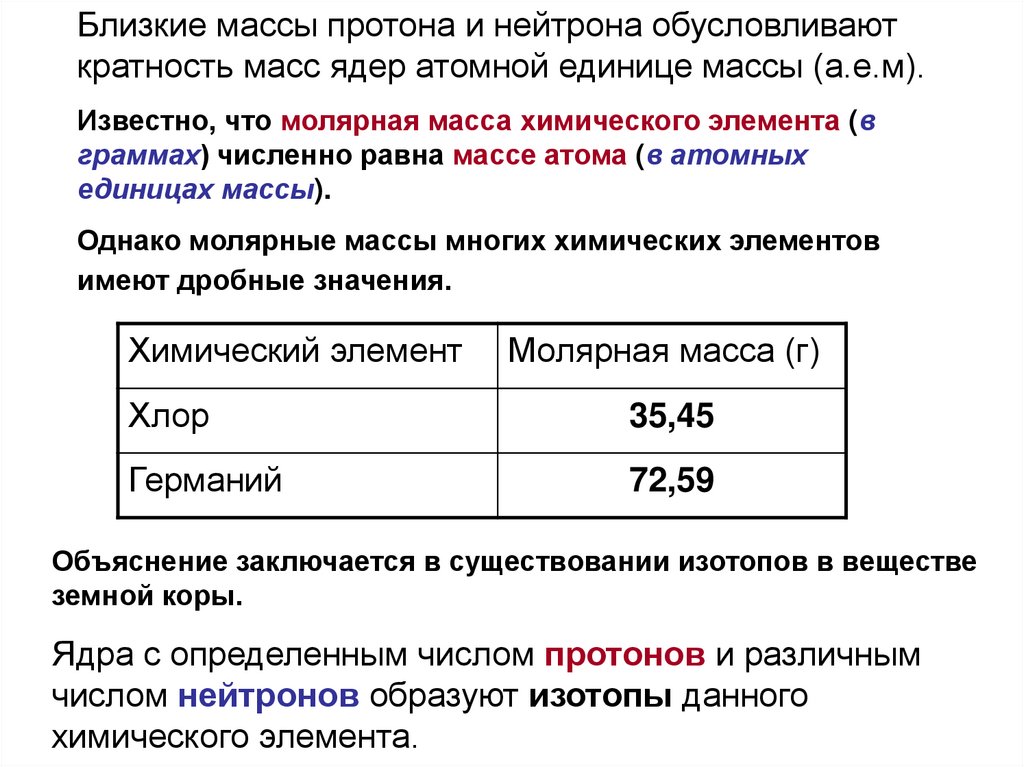
Близкие массы протона и нейтрона обусловливают
кратность масс ядер атомной единице массы (а.е.м).
Известно, что молярная масса химического элемента (в
граммах) численно равна массе атома (в атомных
единицах массы).
Однако молярные массы многих химических элементов
имеют дробные значения.
Химический элемент
Молярная масса (г)
Хлор
35,45
Германий
72,59
Объяснение заключается в существовании изотопов в веществе
земной коры.
Ядра с определенным числом протонов и различным
числом нейтронов образуют изотопы данного
химического элемента.

6.

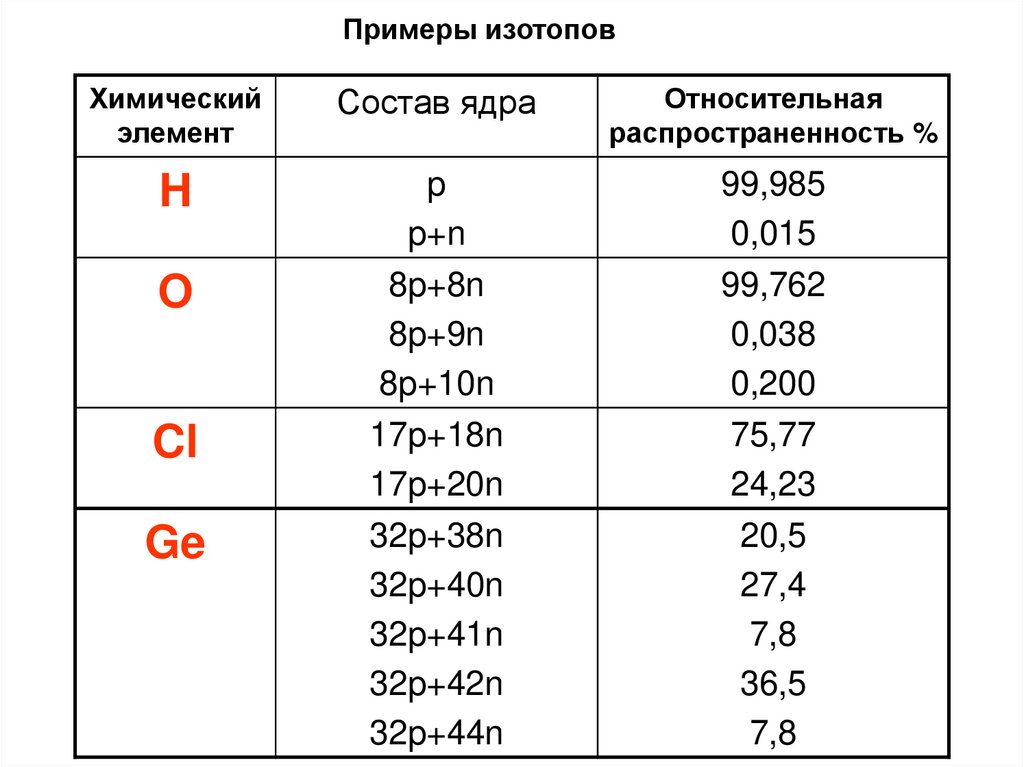
Примеры изотопов
Химический
элемент
Состав ядра
Относительная
распространенность %
H
p
p+n
99,985
0,015
O
8p+8n
8p+9n
8p+10n
99,762
0,038
0,200
Cl
17p+18n
17p+20n
75,77
24,23
Ge
32p+38n
32p+40n
32p+41n
32p+42n
32p+44n
20,5
27,4
7,8
36,5
7,8

7.

Масс-спектрограмма природного кадмия
I (отн.ед.)
Наблюдается 8 стабильных изотопов
Кадмий
30
25
20
15
10
5
0
104
106
108
110
112
114
116
118
M (а.е .м.)
По горизонтали – масса ядра в а.е.м.
По вертикали относительное количество изотопа.
Ширина пика – аппаратурная погрешность

8.

Специальные термины
Чётно-чётные ядра:
число протонов Z чётное, число нейтронов N чётное.
Чётно-нечётные ядра:
число протонов Z чётное, число нейтронов N нечётное.
Нечётно-чётные ядра:
число протонов Z нечётное, число нейтронов N чётное.
Нечётно-нечётные ядра:
число протонов Z нечётное, число нейтронов N нечётное.

9.

Размер ядра
Размеры атомных ядер вычисляются по результатам
рассеяния на них ускоренных протонов, электронов и
нейтронов (с малой длиной волны Де-Бройля).
Размер ядра: ~ 10-12 ÷ 10-13 см
Оценка радиуса:
RN A 10
3
13
см
(1.1)
где A = Z + N (массовое число, т.е. суммарное
количество протонов и нейтронов в ядре).
1 ферми = 10–13 см

10.

Электрический заряд ядра: +Ze
Определяется количеством протонов Z.
e – элементарный заряд.
Электрический дипольный момент ядра
равен нулю.

11. Массовая плотность атомного ядра

Усредненная плотность :
N
MN
(1.2)
3
(4 / 3) RN
Приближенная оценка с помощью формулы (1.1):
N
( Z N ) 1( a.е.m.)
(4 / 3) ( Z N ) (10
13
см )
3
(1.3)

12.

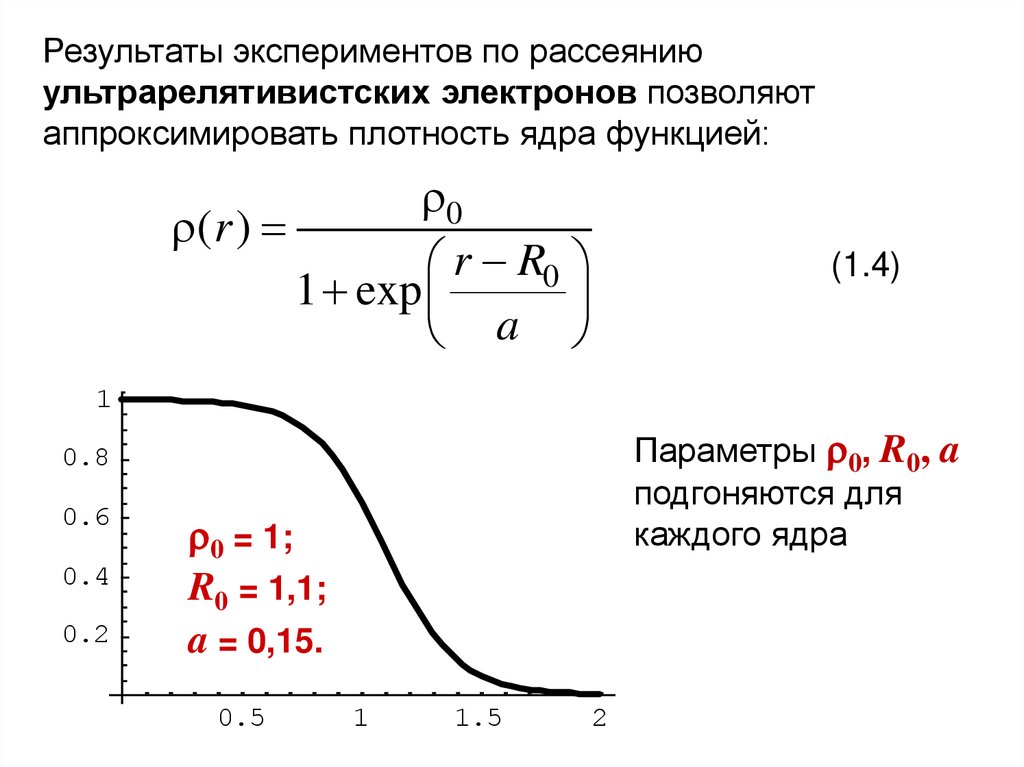
Результаты экспериментов по рассеянию
ультрарелятивистских электронов позволяют
аппроксимировать плотность ядра функцией:
0
( r )
r R0
1 exp
a
(1.4)
1
Параметры 0, R0, a
подгоняются для
каждого ядра
0.8
0.6
0.4
0.2
0 = 1;
R0 = 1,1;
a = 0,15.
0.5
1
1.5
2

13. Спин атомного ядра

Спин ядра складывается из спинов нуклонов и
орбитальных моментов импульса нуклонов,
движущихся в ядре.
Сложение проводится по правилам квантовой механики.
Ядра с четным количеством нуклонов имеют целое
спиновое квантовое число.
Ядра с нечетным количеством нуклонов имеют
полуцелое спиновое квантовое число.
Спины всех четно-четных ядер в основном состоянии
равны нулю.
Спиновые квантовые числа всех стабильных ядер в
основном состоянии не превышают 9/2.

14. Магнитный момент нуклонов и ядер

Проекция магнитного момента пропорциональна
проекции спина (механического момента импульса) :
Z = sZ
(1.5)
– гиромагнитное отношение.
Проекция спина квантуется:
sZ = ħ m s
(1.6)
ms – магнитное квантовое число.
Во внешнем магнитном поле B магнитный момент
приобретает дополнительную энергию
ZB
(1.7)

15.

Метод ядерного магнитного резонанса (ЯМР)
При поглощении резонансного фотона с частотой 0
магнитная энергия (1.7) увеличивается, при этом
магнитное квантовое число mj изменяется на единицу.
Уравнение магнитного резонанса :
ħ 0 = ( Z B)
Подстановка в правую часть выражений (1.5) и (1.6) с
учётом (ms) = 1 даёт:
ħ 0 = ħ B
(1.8)

16.

Метод ядерного магнитного резонанса (ЯМР)
Измерив резонансную частоту 0 , решением
уравнения (1.8) можно вычислить гиромагнитное
отношение
= 0 / B ,
Затем по формуле (1.5) рассчитывается проекция
магнитного момента Z

17.

Скалярный магнитный момент – максимальное
значение проекции магнитного момента на направление
внешнего магнитного поля.
Из вышеприведенных уравнений (1.5) и (1.8) следует, что
= s
или
= ( 0 / B) s
где s – спиновое квантовое число.
(1.9)

18.

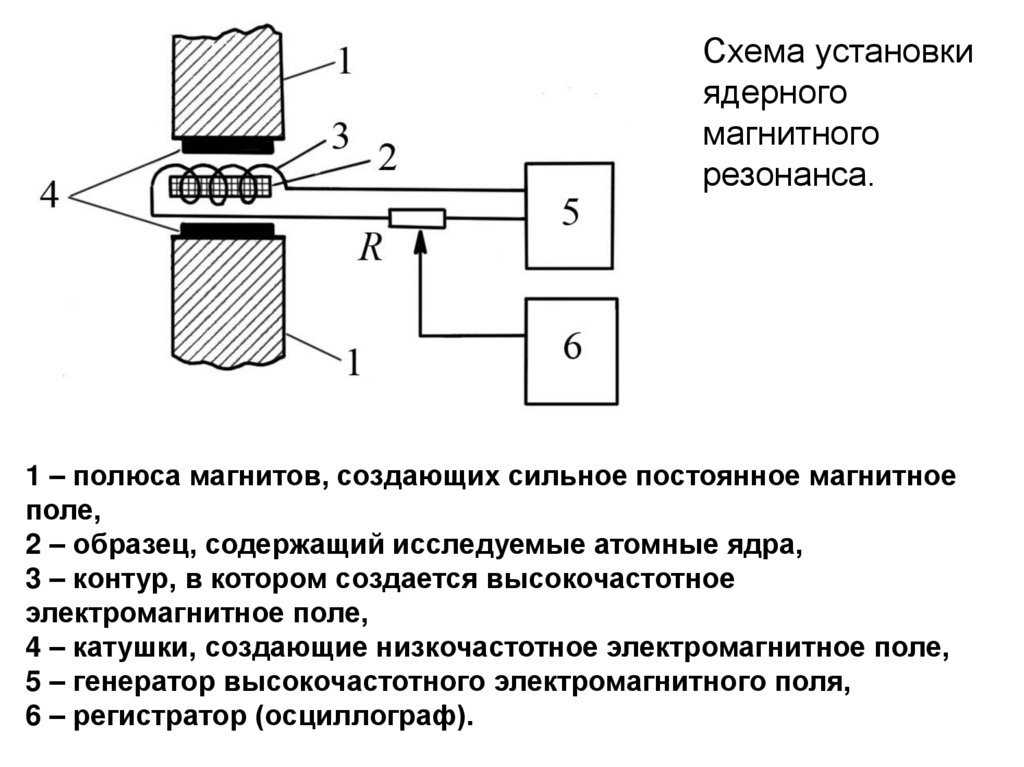
Схема установки
ядерного
магнитного
резонанса.
1 – полюса магнитов, создающих сильное постоянное магнитное
поле,
2 – образец, содержащий исследуемые атомные ядра,
3 – контур, в котором создается высокочастотное
электромагнитное поле,
4 – катушки, создающие низкочастотное электромагнитное поле,
5 – генератор высокочастотного электромагнитного поля,
6 – регистратор (осциллограф).

19.

Спиновое число протона s = 1/2.
Измерения резонансной частоты методом ЯМР и
вычисления по формуле (1.9) дают для протона
= 2,79 0
Единица магнитного момента ядра – ядерный магнетон
e
0
5 10 24 эрг / Гс
2m p c
(1.10)

20.

Магнитный момент нейтрона
Спин нейтрона s = 1/2, и его проекция магнитного момента
может принимать два значения Z.
Во внешнем магнитном поле состояния с + Z. и Z.
имеют энергии, различаются на величину
Е = 2 ZB
(1.11)
Свободный нейтрон – нестабильная частица.
Для измерения магнитного момента нейтрона
используются пучки нейтронов, пропускаемые через
неоднородные магнитные поля. При этом на нейтроны
воздействуют потоком высокочастотного излучения.
Если энергия фотона равна Е, то нейтрон изменяет
свое состояние.

21.

На магнитный момент в неоднородном магнитном поле
действует сила
F μ B
(1.12)
Проекция силы, действующей на магнитный момент
в неоднородном магнитном поле
B y
B Bx
Bz
x
Fz μ
y
z
z
z
z
z

22.

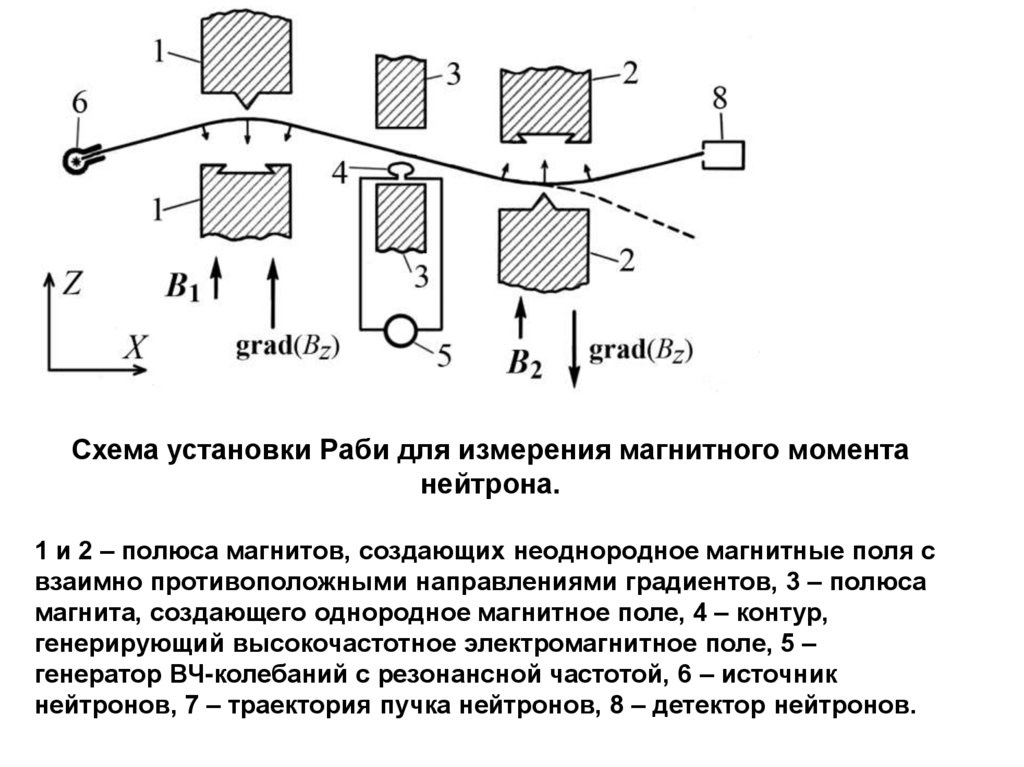
Схема установки Раби для измерения магнитного момента
нейтрона.
1 и 2 – полюса магнитов, создающих неоднородное магнитные поля с
взаимно противоположными направлениями градиентов, 3 – полюса
магнита, создающего однородное магнитное поле, 4 – контур,
генерирующий высокочастотное электромагнитное поле, 5 –
генератор ВЧ-колебаний с резонансной частотой, 6 – источник
нейтронов, 7 – траектория пучка нейтронов, 8 – детектор нейтронов.

23.

При поглощении резонансного фотона с энергией = Е
изменяется на противоположную ориентация магнитного
момента и направление действующей силы (1.12).
Измерения резонансной частоты позволяют
вычислить для нейтрона = – 1,91 0 .
Отрицательный знак означает, что спин и магнитный
момент антипараллельны.

24.

Магнитные моменты ядер
Изотоп
Квантовое число
спина ядра
Магнитные моменты ядер в
ядерных магнетонах
7Li
3/2
3,2564
14N
1
0,40376
19F
1/2
2,6289
23Na
3/2
2,2175
27Al
5/2
3,6415
51V
7/2
5,151
55Mn
5/2
3,47
59Co
7/2
4,6
93Nb
9/2
6,17
127I
5/2
2,81
133Cs
7/2
2,582
197Au
3/2
0,146
209Bi
9/2
4,3

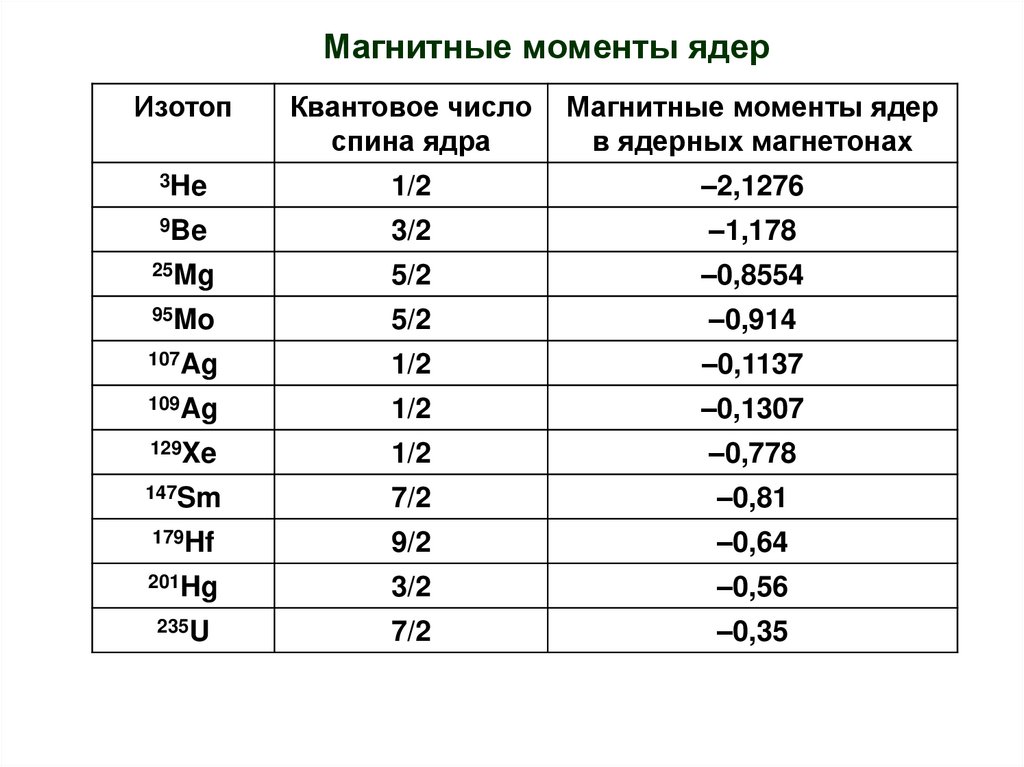
25.

Магнитные моменты ядер
Изотоп
Квантовое число
спина ядра
Магнитные моменты ядер
в ядерных магнетонах
3He
1/2
–2,1276
9Be
3/2
–1,178
25Mg
5/2
–0,8554
95Mo
5/2
–0,914
107Ag
1/2
–0,1137
109Ag
1/2
–0,1307
129Xe
1/2
–0,778
147Sm
7/2
–0,81
179Hf
9/2
–0,64
201Hg
3/2
–0,56
235U
7/2
–0,35

26. Квадрупольный электрический момент ядра

Мера отклонения распределения электрического заряда
от сферической симметрии.
1
2
2
Q0
e (r )(3 z r )dV
e
(1.13)
V
e – плотность распределения электрического заряда.
При Q0 0 распределение заряда - эллипсоид вращения.
Для ядра, вытянутого вдоль направления вектора спина,
квадрупольный электрический момент Q0 положителен;
для ядра, сплющенного в этом направлении, Q0 < 0.
При сферическом распределении заряда в ядре Q0 = 0.

27.

Квадрупольный электрический момент Q0 определен в
собственной системе координат.
Вследствие вращательного движения атомного ядра
измеряемый квадрупольный электрический момент
равен:
s ( 2 s 1)
Q
Q0
( s 1)( 2 s 3)
где s – спиновое число ядра.
(1.14)

28.

В неоднородном электрическом поле квадрупольный
электрический момент приобретает дополнительную
энергию.
2
2
3ms s ( s 1)
(1.15)
EQ
eQ 2
4 s ( 2 s 1)
z
– потенциал внешнего электрического поля
Для измерения квадрупольного электрического момента
ядра используется ядерный квадрупольный резонанс.

29.

Результаты измерений квадрупольного электрического
момента некоторых ядер
Ядро
Q (барн)
Ядро
Q (барн)
2
H
1
0,0027
59
Co
27
0,404
14
N
7
0,0071
85
Rb
37
0,27
17
8O
-0,027
73Ta
27
Al
13
0,140
204
Bi
81
-0,19
33
S
16
-0,064
233
U
92
3,4
181
6
1 барн = 10 24 см2

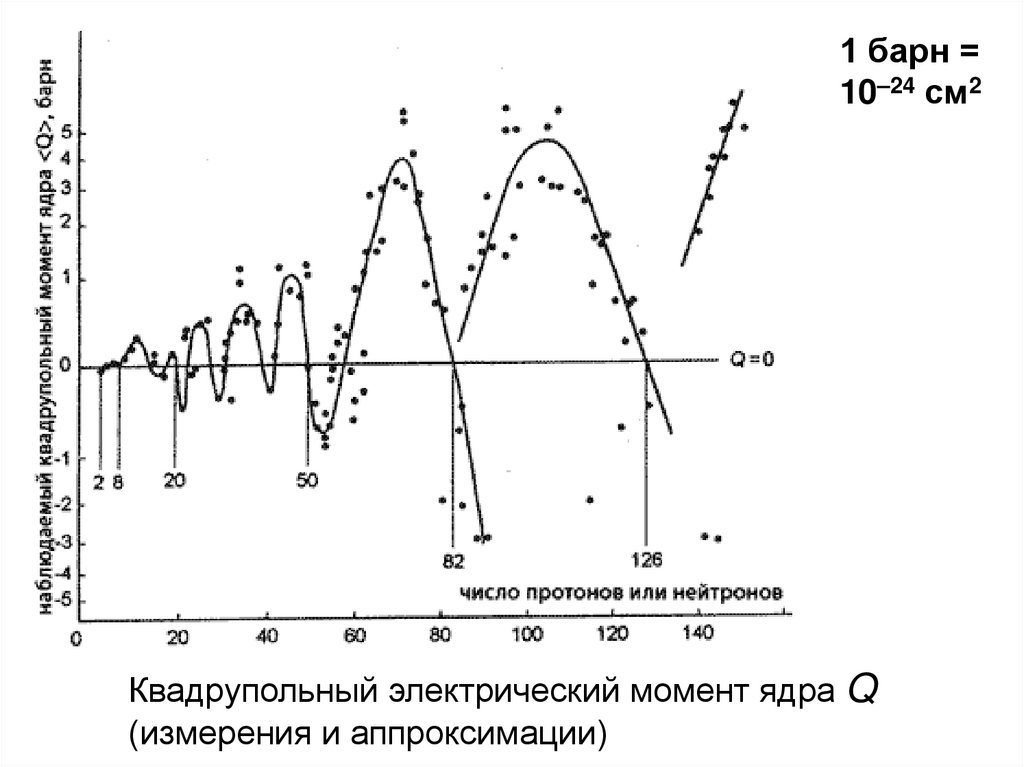
30.

1 барн =
10 24 см2
Квадрупольный электрический момент ядра Q
(измерения и аппроксимации)

31.

Межнуклонное взаимодействие
Нуклоны (протоны и нейтроны) удерживаются в ядре
силами притяжения.
Силы межнуклонного притяжения компенсируют силы
кулоновского расталкивания между протонами.
Силы межнуклонного притяжения являются
короткодействующими. Это обусловливает размер ядра
и количество нейтронов в стабильных ядрах.
mp mn 1 а.е.м.= 1,6606 10–24 г
mn mp + 2,5 me

32.

Дефект массы ядра
m = Zmp + Nmn – Mя
Обнаружен средствами
прецизионной масс-спектрометрии
(1.16)

33.

Энергия связи нуклонов в ядре
Энергия, необходимая для разделения ядра на
составляющие его нуклоны.
Есв = m с2 = (Zmp + Nmn – Mя) с2
(1.17)
Пример.
Альфа-частица состоит из двух протонов и двух
нейтронов.
Масса альфа-частицы: 6,644656×10−24 г
Расчет по формуле (1.17) дает для альфа-частицы:
Есв = 28,3 МэВ

34.

Удельная энергия связи нуклонов в ядре
= Есв /(Z + N) = Есв / A
(1.18)
Энергия связи, приходящаяся на один нуклон в ядре.

35.

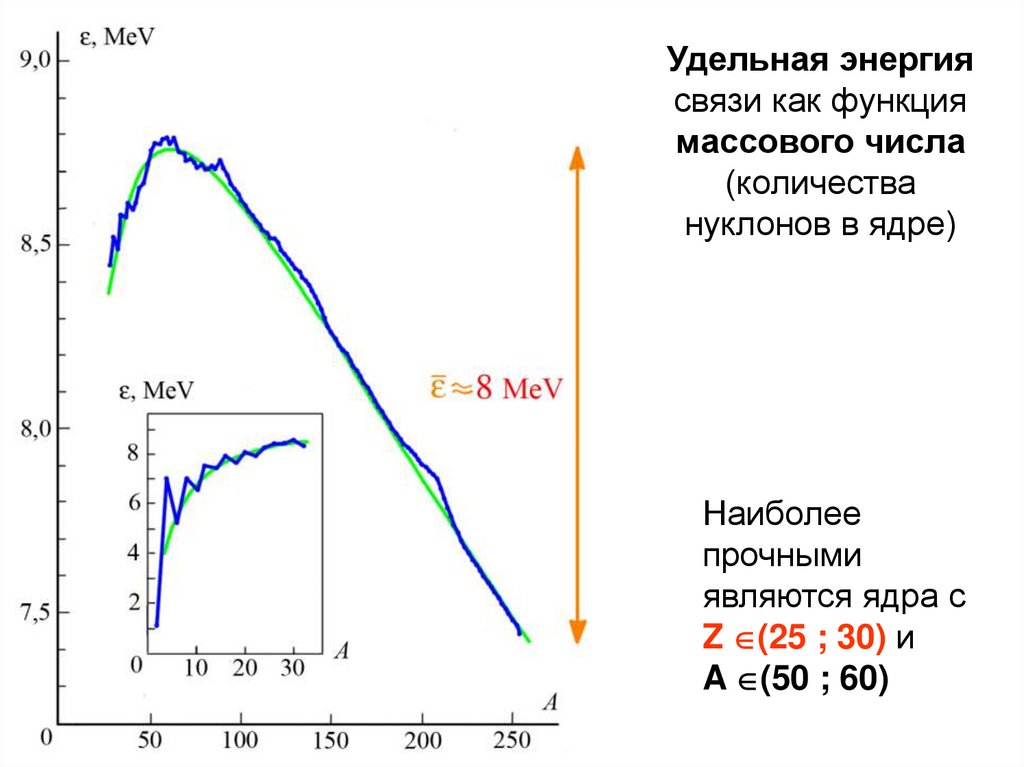
Удельная энергия
связи как функция
массового числа
(количества
нуклонов в ядре)
Наиболее
прочными
являются ядра с
Z (25 ; 30) и
A (50 ; 60)

36. Формула Вайцзеккера

Есв a1 A a2 A
23
a3 Z A
2
1 3
( A 2Z )
a4
A
2
(1.19)
a1 = 15,75 МэВ; a2 = 17,8 МэВ; a3 = 0,7 МэВ; a4 = 23,7 МэВ
(четно четные ядра)
( нечетно нечетные ядра)
= 12/A1/3 МэВ

37.

Карл Фридрих фон Вайцзеккер
(1912 2007)
Германский физик, философ и
политический деятель.

38.

130
Протоннейтронная
диаграмма
стабильных
ядер
N
120
110
100
90
80
70
60
50
40
30
20
10
Z
0
0
10
20
30
40
50
60
70
80
90
N Z если Z 20
N > Z если Z > 20