Похожие презентации:
Обобщение понятия о показателе степени
1.
Обобщение понятия опоказателе степени.
mathvideourok.moy.su
2.
рОпределение : Если обыкновенная дробь
q
(q 1) и а 0, то
р
q
а а
q
р
Например :
1
2
в) 3 2 2
1)а)3 3
5
4
б )7 7
4
5
1
3
г) 2 2
4
3
3
4
3.
2) Вычислите :1
6
2
3
б )27 27 3 9
а)64 64 2
51
4
6
3
2
2
в)0 0 0
1
г) 8 3 не имеет смысла !!! так как 8 0, но
4
51
3
1
3
8 1
3
8 2
8 3 8
2
6
8 2
!!!
( 8) 64 2
получаем, что 2 2 1
таким образом 8 3 не имеет смысла
6
2
6
4.
рОпределение : Если обыкновенная дробь
q
(q 1) и а 0, то
р
1
a
р
q
a
р
q
а
q
1
a
р
q
, а 0
5.
а)31
2
1
3
б )7
5
4
1
2
1
3
1
2
1
4
7
в)64
5
1
6
1
1
6
64 2
1
г )0 не имеет смысла
0
6.
Основные свойства степенейа a a
m
n
а :a a
m
n
a
m n
a
ав
m n
m
а в
m m
m
m n
а
а
m
в
в
mn
m
Если a 1, то если
0 a в, то
если r 0, то а в
r
если r 0, то а в
r
r
r
r s, то a a
Если 0 a 1, то если
r
r s, то a a
r
s
s
7.
1) Найти значение выражения4
1
4
40 2 : 5
3
4
4
40 2
4
5
3
4
4
3
4
80 5 16 5 5
4
4
2 5 2 5 10
2) Преобразуйте выражения
а)
1
2
1
2
1
4
1
4
а в
а в
1
4
4
1
4
1
4
1
4
1
4
1
4
( а в )(а в )
а в
4
1
4
а в
1
4
3
8.
а в(а 0,4 )3 (в 0,7 )3
б ) 0,8
0,8
0,4 0,7
1,4
0,4 0,7
1,4
а а в в
а а в в
1,2
2,1
(а 0,4 в 0,7 )(а 0,8 а 0,4в 0,7 в1,4 )
0,4
0,7
а в
0,8
0,4 0,7
1,4
а а в в
9.
3) Сравните числаа) 8 и 2
5
3
5
2 и2
2 1
2
3
2
3
3
2
<
5
3
3
5
2 <2
8 2 2
5
3
2 10
3 15
3 9
;
5 15
IIспособ:
а) 8 и 2
5
2
3
Ответ : 8 < 2
5
5
3
5
5
2
3
2
3
8 2 2
5
2
3
3
15
9
2 2 2
3
2
15
10
Ответ : 5 8 < 2
2
3
10.
15
б )0,5 и 0,5
2
5
0 0,5 1
1 2
, значит
5 5
1
5
0,5 > 0,5
2
5
Если a 1, то если
r s, то a a
Если 0 a 1, то если
r
r s, то a a
r
s
s
11.
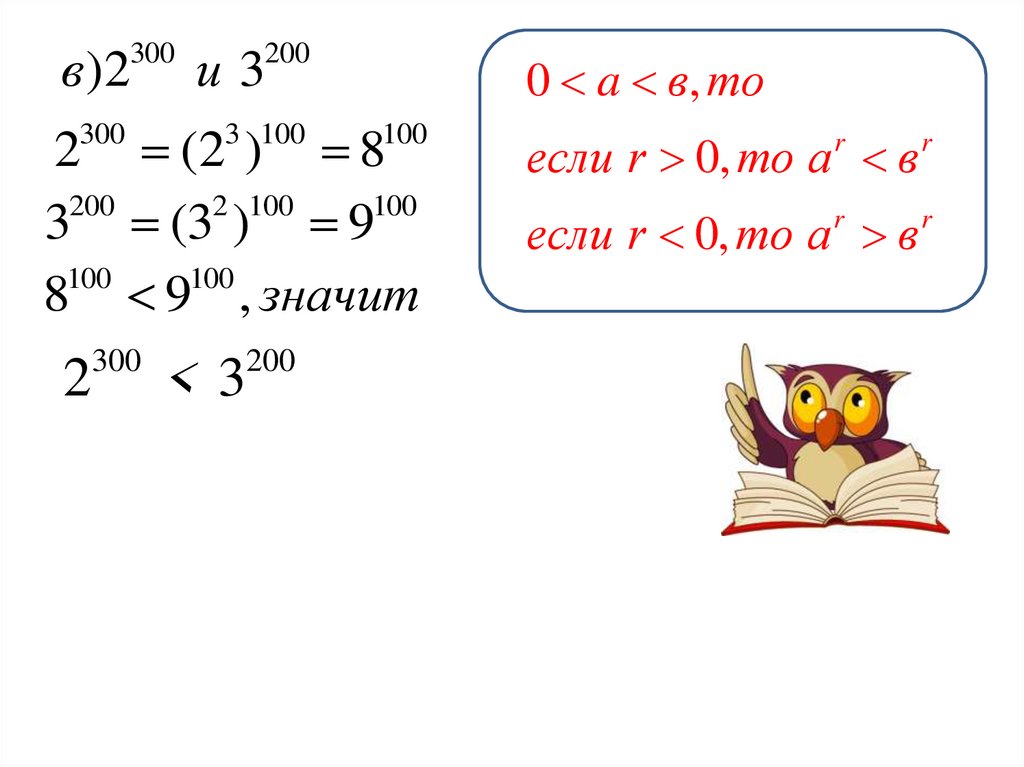
в)2300
и3
200
0 a в, то
2 (2 ) 8
200
2 100
100
3 (3 ) 9
100
100
8 9 , значит
300
2
300
3 100
200
<3
100
если r 0, то а в
r
r
если r 0, то а r в r
12.
г )22
20
20
30
и3
1
2
20
1
2
1
1
3
3
30
30
3
10
2 10
10
1
4
3 10
10
1
27
10
1
1
, значит
4
27
2
20
30
>3
13.
4) Упростите выражение:2
1
3
х у 2 ху 3 2
( у)
1
3
1
3
2
3
1
3
1
3
2
3
1
3
1
3
2
3
х 2х у у 2х у у х
5) Решите уравнение
а) х 1
2
х 1
3
2
х 1
Ответ : 1
2
3
14.
23
б) х 1
ОДЗ : х 0 (согласно определению)
3
3
х 1
2
3
х 1
2
х 1
1 не входит в ОДЗ
Ответ :1
15.
23
1
3
1
3
в) х 2 х 8 0
2
п 2п 8 0
Пусть х п, х 0
п 0
1 3
п1;2
1
Д
1 8 9 0(2к )
4
1
3
п1 4
п2 2
1)если п 2, то х 2
корней нет
2)если п 4, то х
1
х
1
3
4
1
3
1
3
1
х
4
4
1
х
16
1
Ответ :
16
16.
6) Вычислить:1
2
1
4
1
8
1
16
5 3 5 3... 5 3 5 3 ... 5
Найдем 5
1 1
...
2 8
5 3 5 3...
1 1
...
2 8
3
1 1
...
4 16
1 1
... бесконечная
2 8
геометрическая прогрессия
в2
q= 1 : 1 1 2 1
в1
8 2 8 1 4
1
в1
2 2
Sn
1 q 1 1 3
4
5
1 1
...
2 8
2
3
5 5
3
2
17.
Найдем 31 1
...
4 16
1 1
... бесконечная
4 16
геометрическая прогрессия
в2
1
1
1
4
1
q=
:
в1 16 4 16 1 4
1
в1
1
4
Sn
1 q 1 1 3
4
Получается
5
1 1
...
2 8
3
3
1 1
...
4 16
1 1
...
4 16
Ответ :
1
3
3 3
3
5 3 75
3
2
3
3
5 3 5 3... 3 75




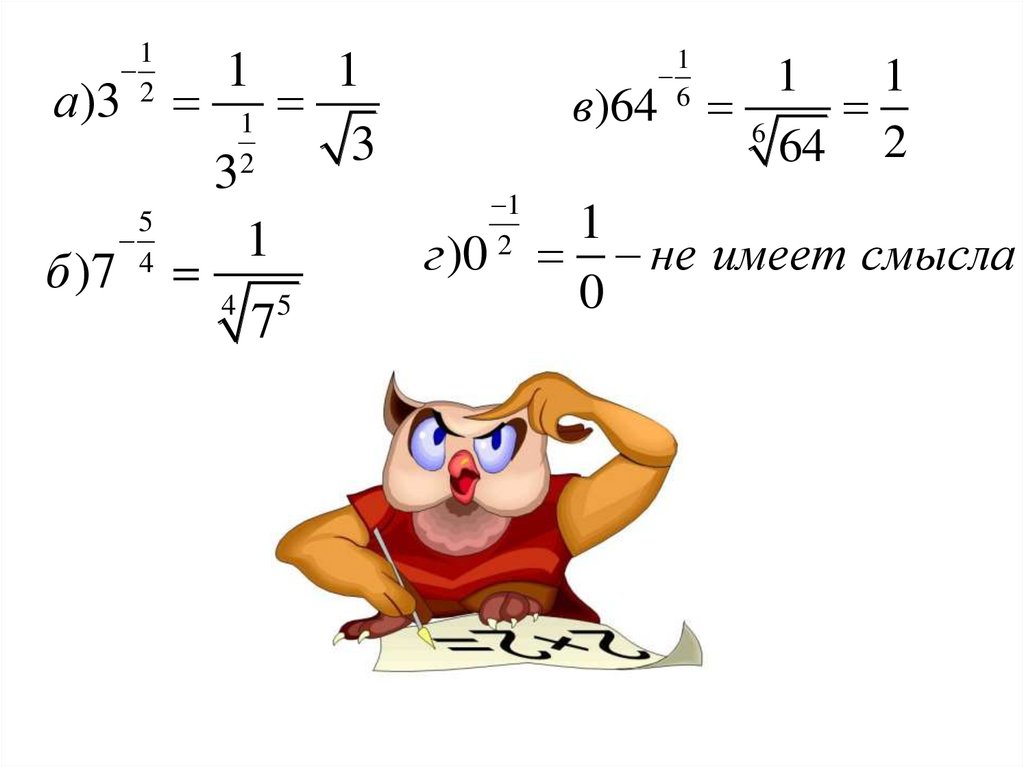





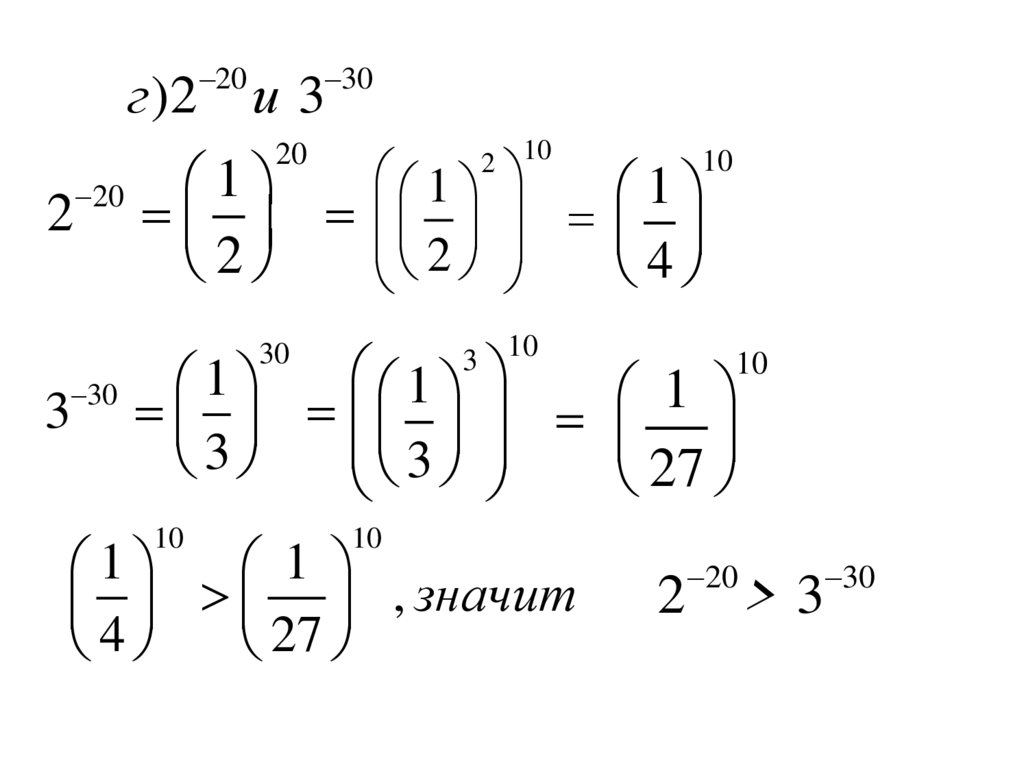


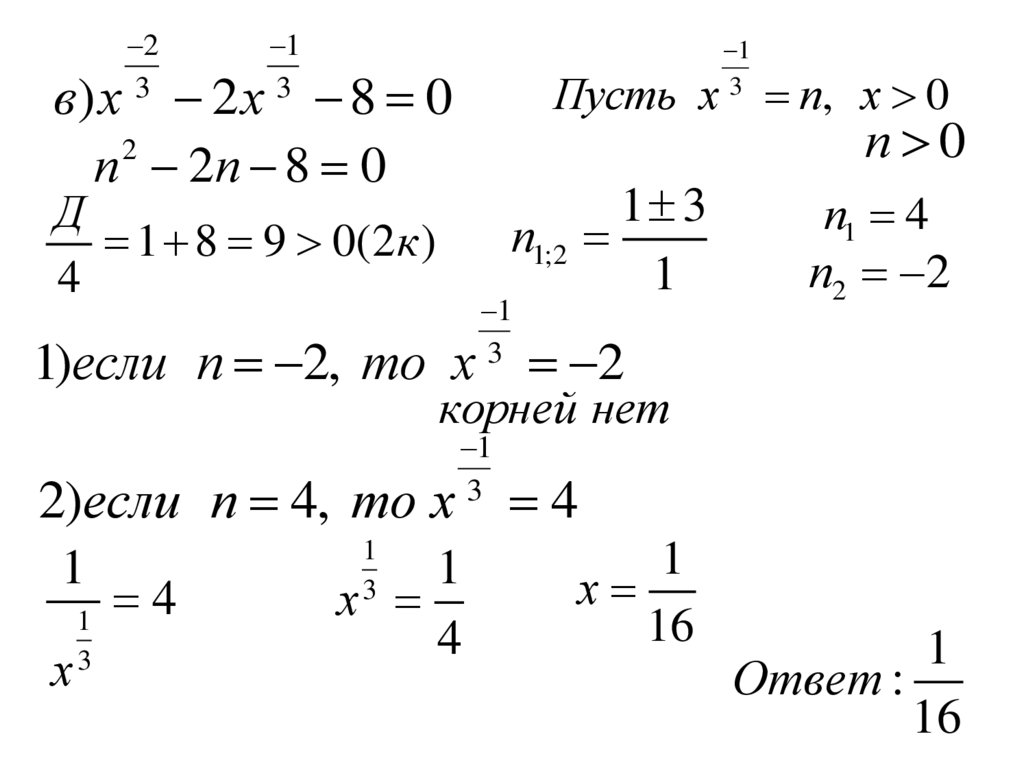


 Математика
Математика








