Похожие презентации:
Степень с рациональным показателем и ее свойства
1. Степень с рациональным показателем и ее свойства.
2.
ПовторениеСтепень с целым показателем
a a a ... a
n
1)3 27
3
2)5 125
3
3)2 16
4
4)3 3
1
Степенью числа а с
натуральным показателем n,
большим 1, называется
произведение n множителей,
каждый из которых равен а
3.
mn m
n
n
1)a a a
n
m
n m
2)a : a m a
n
n m
3) a a
n
n
n
4) a b a b
n
a a
5) n
b b
4.
1a n
a
a 0
n
a 1
0
5.
11
а) 10 6
;
10
1000000
1
1
2
б) 9 2 ;
9
81
1
1
в) а 1 ;
а
1
20
г) х 20 ;
х
1
3
д) ав
;
3
ав
1
4
е) а в
.
4
а в
6
1)3 1
0
2)5 1
0
3)22222222 1
0
4)100000 1
0
6. Арифметический корень натуральной степени Определение
Корнем n-ой степени из числа aназывается такое число, n-я
степень которого равна a.
n
a x,
то есть x a
n
7.
АРИФМЕТИЧЕСКИЙ КОРЕНЬn-Й СТЕПЕНИ ИЗ ЧИСЛА а
а – ПОДКОРЕННОЕ ВЫРАЖЕНИЕ
8.
ТождестваДЕЙСТВИЕ, ПОСРЕДСТВОМ КОТОРОГО
ОТЫСКИВАЕТСЯ КОРЕНЬ n – Й
СТЕПЕНИ, НАЗЫВАЕТСЯ
ИЗВЛЕЧЕНИЕМ КОРНЯ n – Й СТЕПЕНИ.
9. Примеры
31)
27 3; 33 27
2)
4
256 4 ;
3)
5
0,00243 0,3;
0,35 0 ,00243
4)
3
1000000 100 ;
100 3 1000000
5)
3
64000 40 ;
40 3 64000
1
1
;
64 2
6
6)
6
4 4 256
1
1
64
2
10.
Вычислите:4
16 2
7
0 8 256 0 2 2
5
32 2
3
125 4 81 5 3 8
10
4
1 1
81 3
64 243 8 3 5
5
6
64 4 625 2 5 7
11. Свойства корня n-ой степени (для n ∈ N, m ∈ N, n > 1, m > 1)
Свойства корня n-ой степени(для n ∈ N, m ∈ N, n > 1, m > 1)
1
n
2
n
a
a
n
n ,
b
b
3
4
ab n a n b ,
где a 0 , b 0
где a 0 , b 0
a a , где a 0
n
m
n m
a nm a , где a 0
n
m
12. Понятие степени с рациональным показателем
mn
a a , где a 0, n N , m Z
n
m
Примеры
a
p
1)
2)
3)
2
3
5 3 5 2 3 25
7
5
121,4 12 5 127
4
9
2
2
5
4
9
12
5
4
9
5
12
12
9
4
5
13. Представьте степень с дробным показателем в виде корня:
1.2.
2
3
2
3
1
3
3. 8
5.
2
2
1
3
1
3
1
3
3
не имеет смысла
1
5а 2 5 а
1, 5
4.
3
х у х у
2
3
3
2
14. Представьте в виде степени с дробным показателем:
nа a
m
7 7
1.
2.
m
n
9
1
2
а а
4
4
9
1
3
3 2 2
3.
2
1
Представьте в
виде степени с
дробным
показателем:
4. b
b b b b
5.
х у x y x y
2
3
1, 5
3
2
1,5
15.
mn
a a
km
kn
nk
а
mk
где a 0, n, k N , m Z
2
3
4
6
2 2 2
10
15
16. Свойства степени с рациональным показателем (для p ∈ R, q ∈ R)
1a 0 1,
2
a1 a
где a 0
1
, где a 0
a
1
р
4 a р , где a 0
a
3
a 1
a
10
b
7
a a
p q
pq
8 a p b p ab
p
9
5 a p a q a p q
p
6
ap
p q
a
, где a 0
q
a
p
p
ap a
, где b 0
p
b
b
b
, где a 0, b 0
a


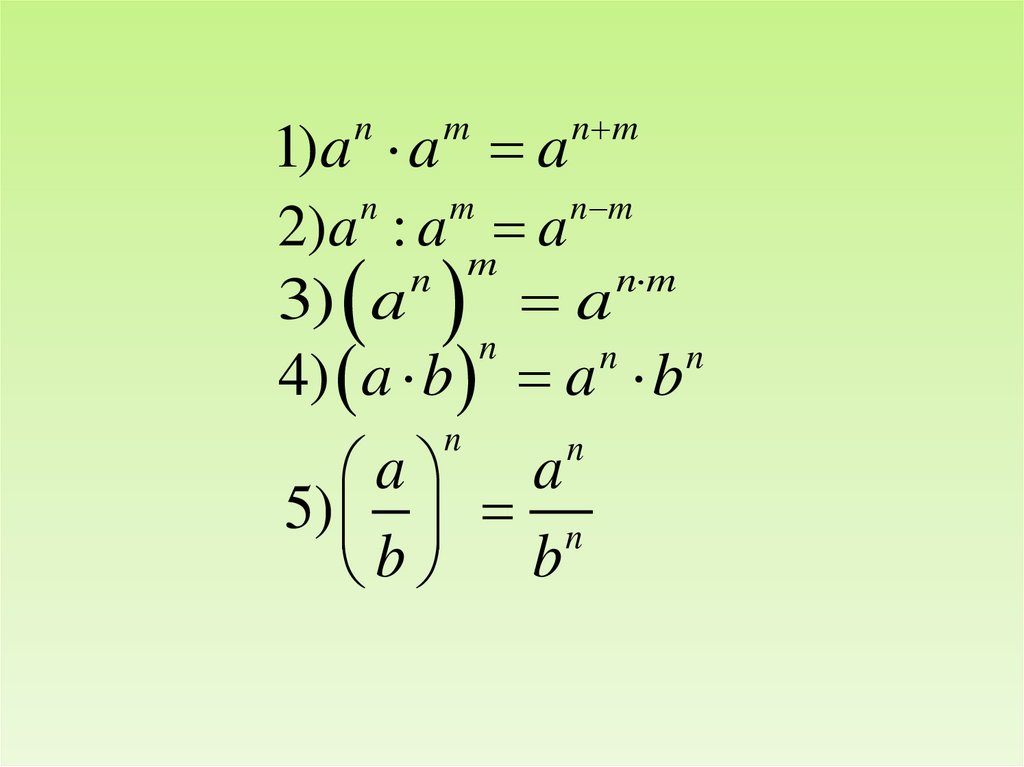

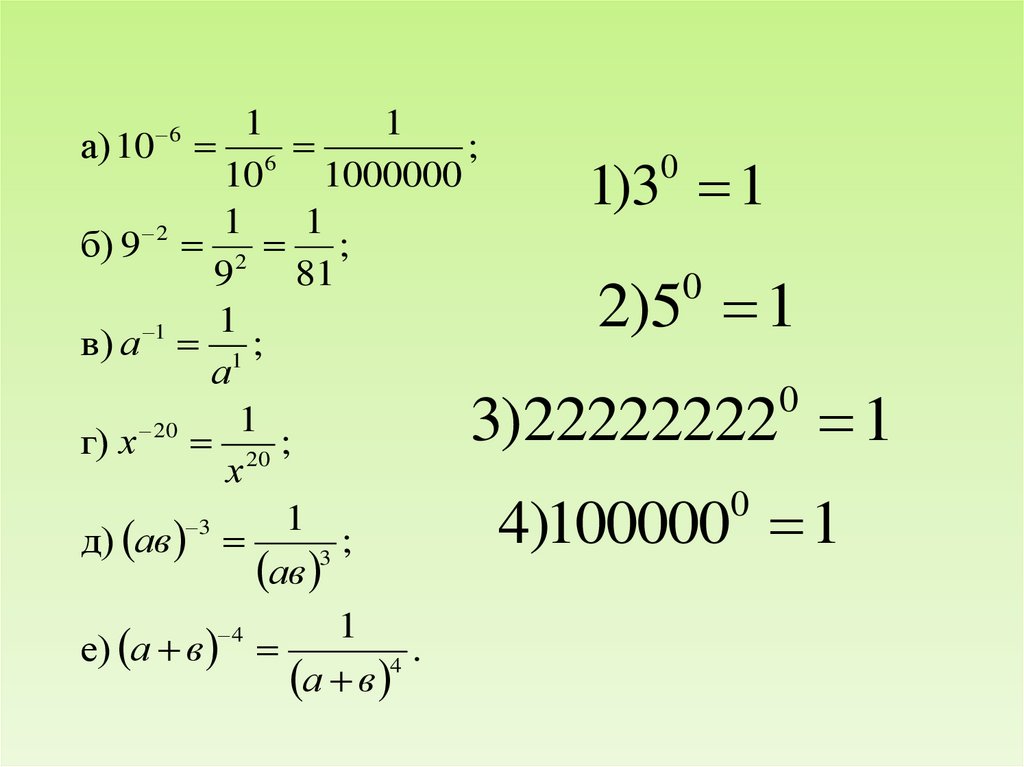









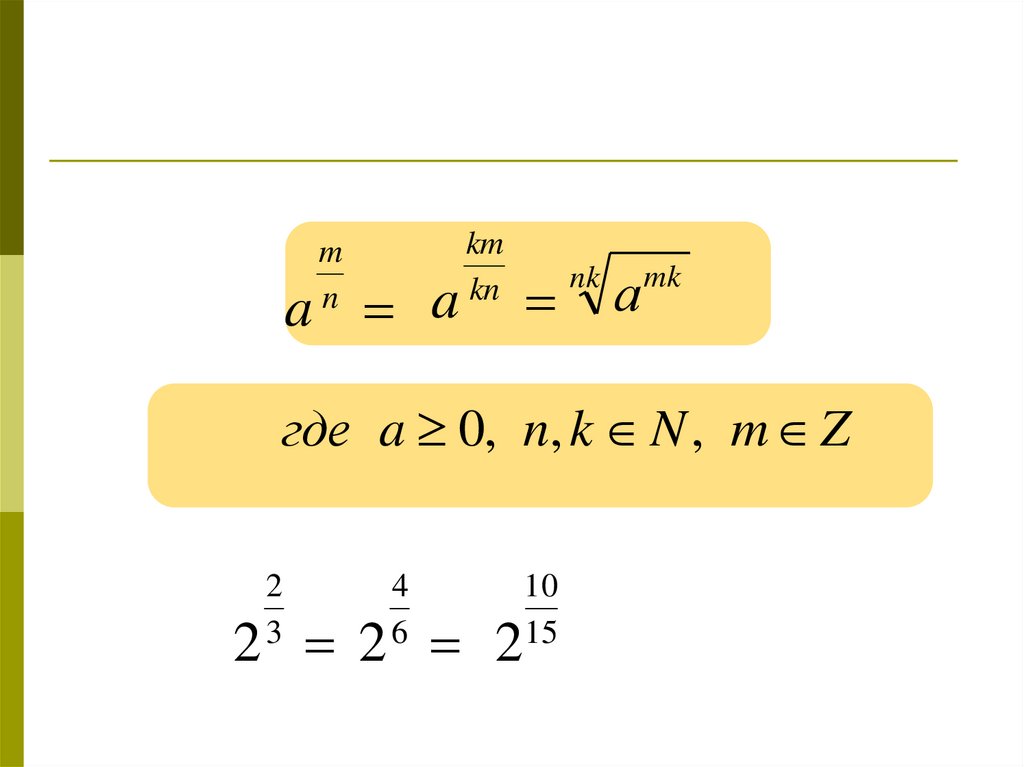

 Математика
Математика








