Похожие презентации:
Теоремы динамики механической системы. Масса механической системы. (Лекция 4)
1. Общие теоремы динамики механической системы
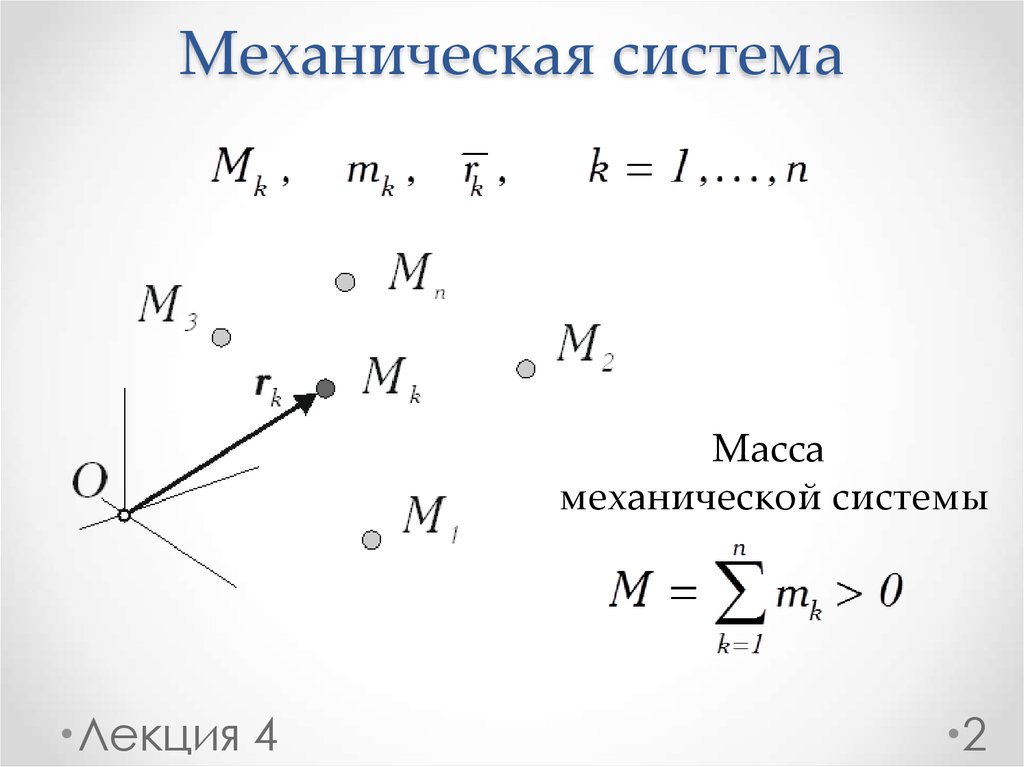
2. Механическая система
Массамеханической системы
Лекция 4
2
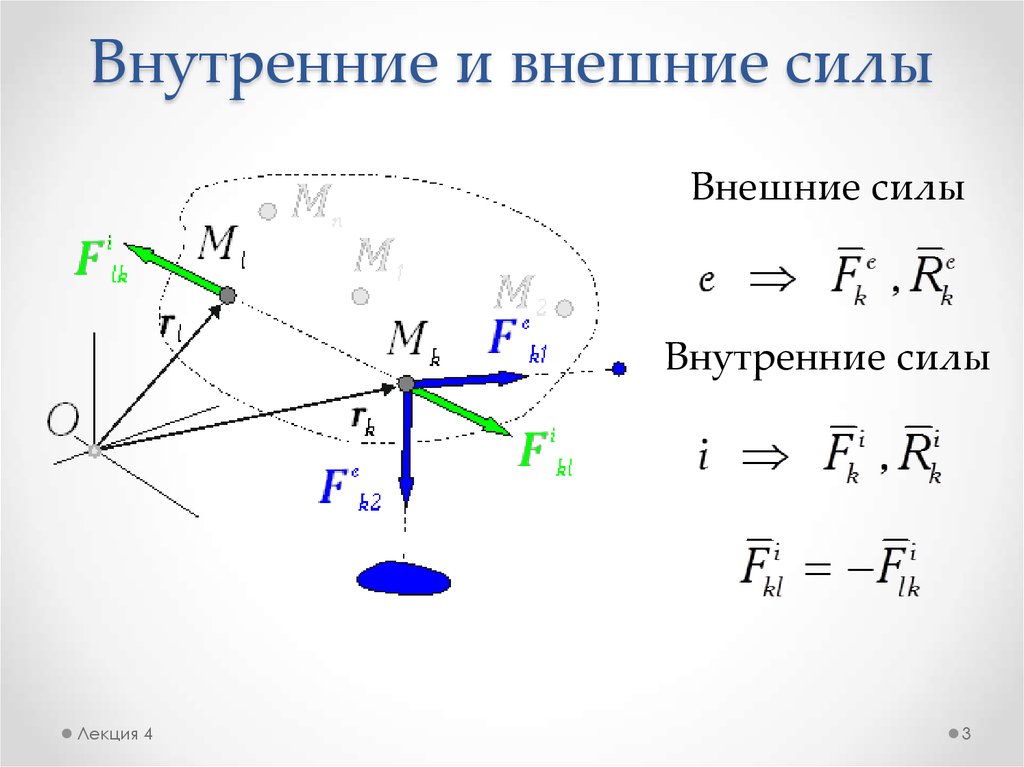
3. Внутренние и внешние силы
Внешние силыВнутренние силы
Лекция 4
3
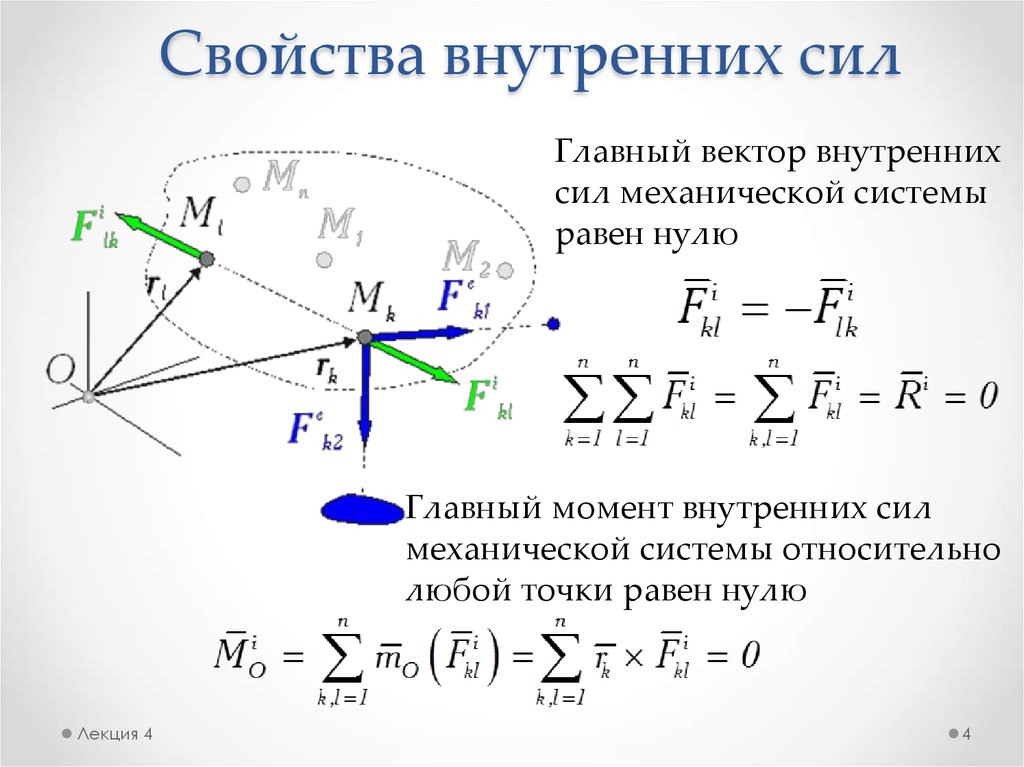
4. Свойства внутренних сил
Главный вектор внутреннихсил механической системы
равен нулю
Главный момент внутренних сил
механической системы относительно
любой точки равен нулю
Лекция 4
4
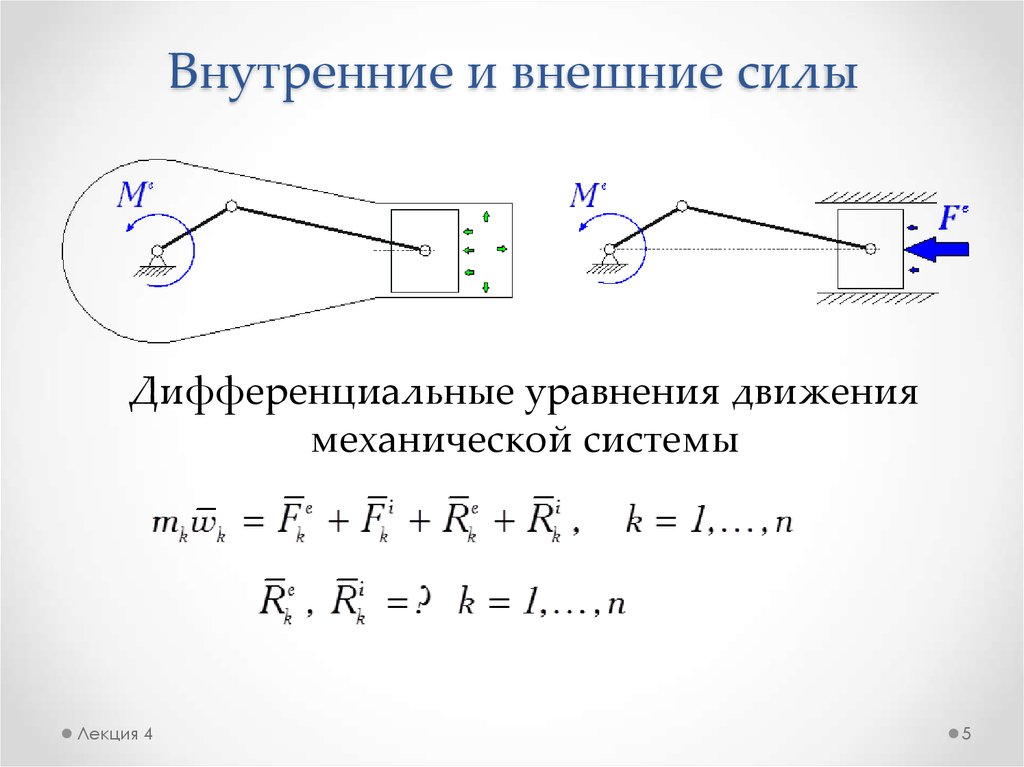
5. Внутренние и внешние силы
Дифференциальные уравнения движениямеханической системы
Лекция 4
5
6. Центр масс
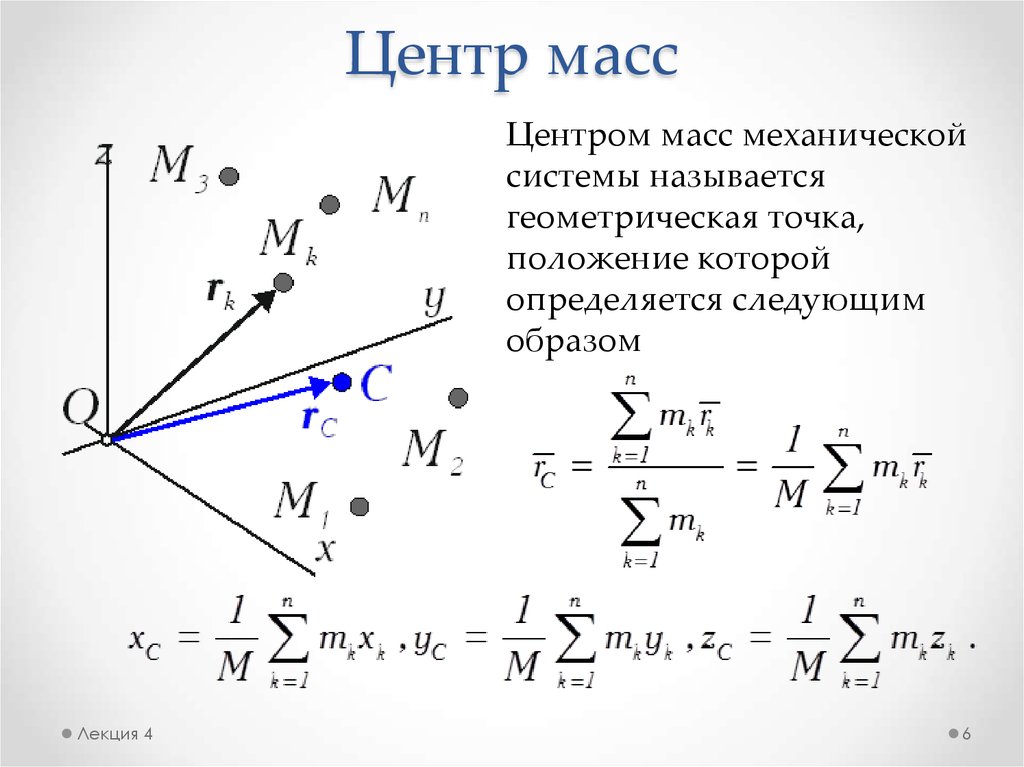
Центром масс механическойсистемы называется
геометрическая точка,
положение которой
определяется следующим
образом
Лекция 4
6
7. Центр масс
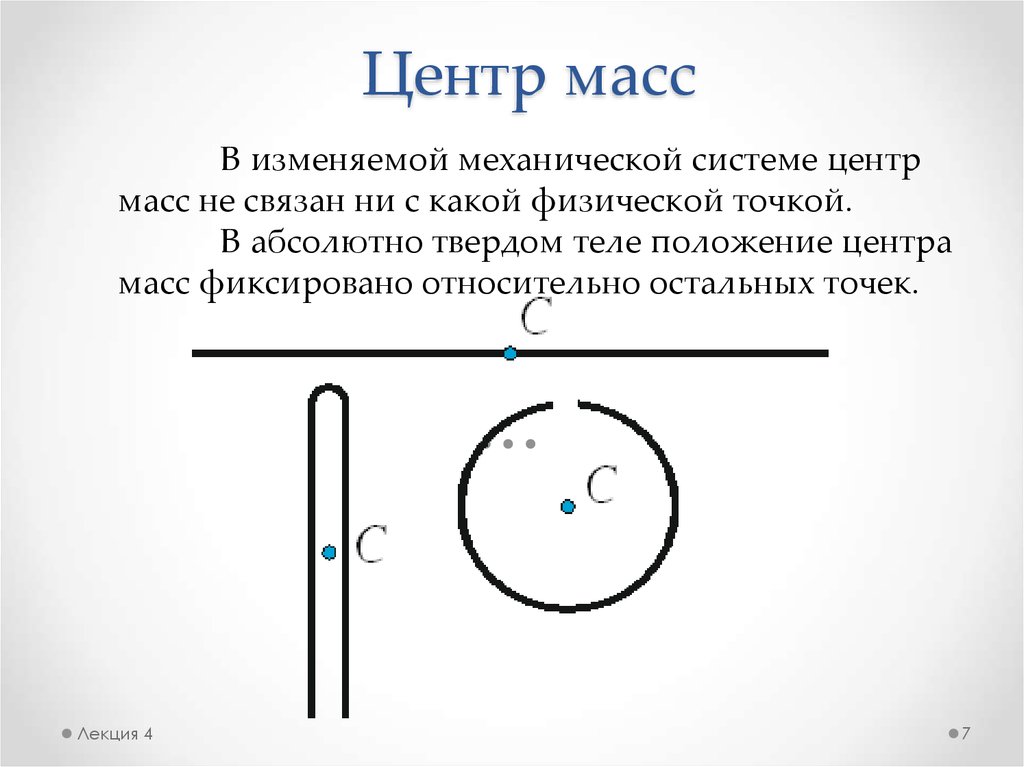
В изменяемой механической системе центрмасс не связан ни с какой физической точкой.
В абсолютно твердом теле положение центра
масс фиксировано относительно остальных точек.
Лекция 4
7
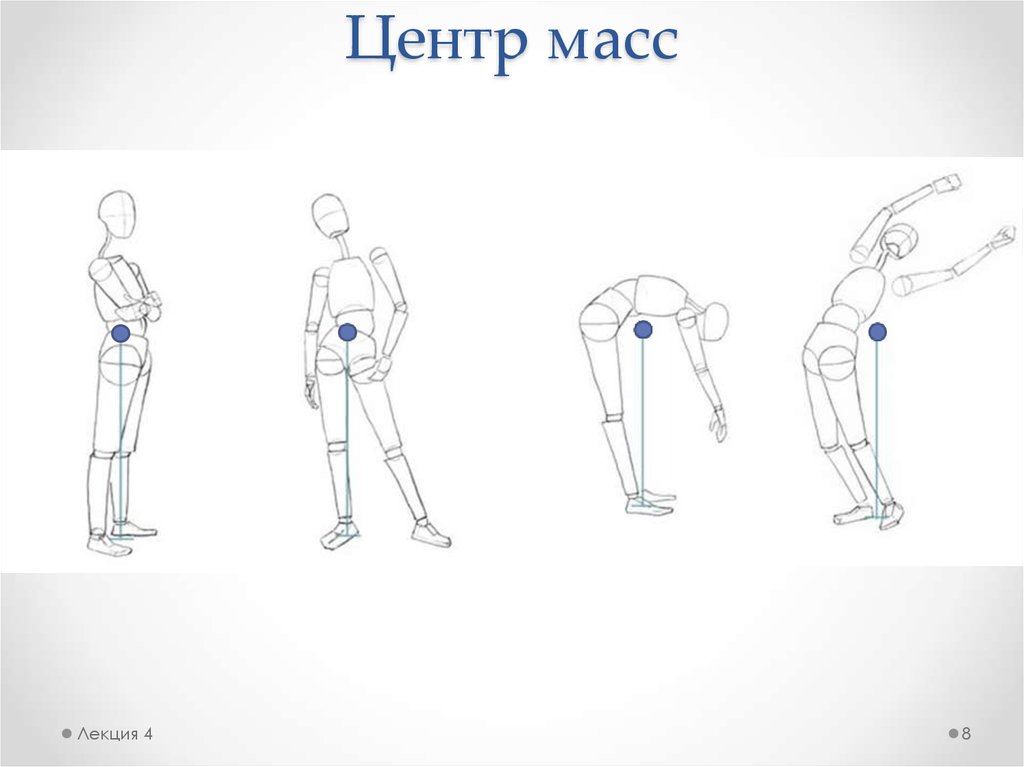
8. Центр масс
Лекция 48
9. Центр масс
Лекция 49
10. Теорема о движении центра масс механической системы
Центр масс механической системы движется так, какдвигалась бы точка, масса которой равна массе
механической системы, под действием одной силы, равной
главному вектору всех внешних сил, приложенных к
точкам и телам системы.
Лекция 4
10
11. Теорема о движении центра масс механической системы
Лекция 411
12. Теорема о движении центра масс механической системы
Следствие 1. Если главный вектор внешних сил, приложенных к точками телам механической системы, равен нулю, то центр масс этой
системы или покоится, или движется равномерно и прямолинейно.
Следствие 2. Если проекция главного вектора внешних сил,
приложенных к точкам и телам механической системы, на какую-то ось
равна нулю, то проекция центра масс этой системы на эту ось или
остается в покое, или движется вдоль оси равномерно и прямолинейно.
Лекция 4
12
13.
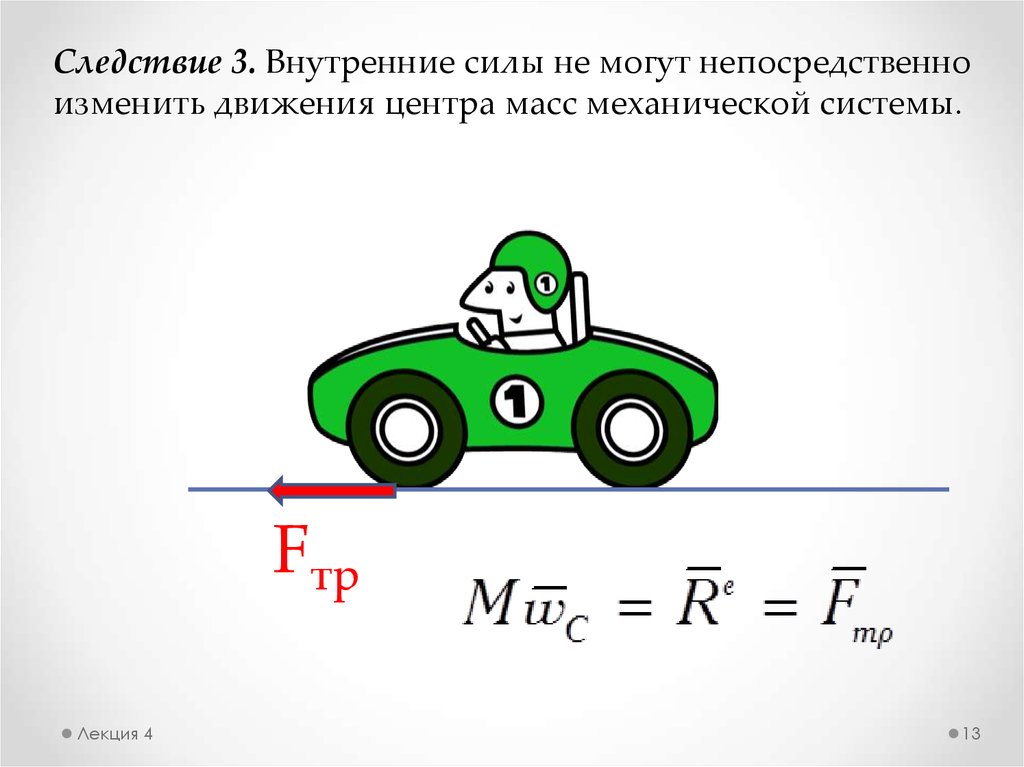
Следствие 3. Внутренние силы не могут непосредственноизменить движения центра масс механической системы.
Fтр
Лекция 4
13
14. Главный вектор количества движения механической системы
Для материальной точкиДля механической системы
Лекция 4
14
15. Теорема об изменении количества движения механической системы
Полная производная по времени от главного вектораколичества движения механической системы по величине
и направлению совпадает с главным вектором внешних
сил, приложенных к точкам и телам этой системы.
Доказательство
Лекция 4
15
16.
Следствие 1. Если главный вектор внешних сил, приложенных кточкам и телам механической системы, равен нулю, то главный
вектор количества движения этой системы остается неизменным.
Следствие 2. Если проекция главного вектора внешних сил,
приложенных к точкам и телам механической системы, на какуюто ось равна нулю, то проекция главного вектора количества
движения системы на эту ось остается неизменной.
Следствие 3. Внутренние силы не могут непосредственно
изменить главный вектор количества движения механической
системы.
Лекция 4
16
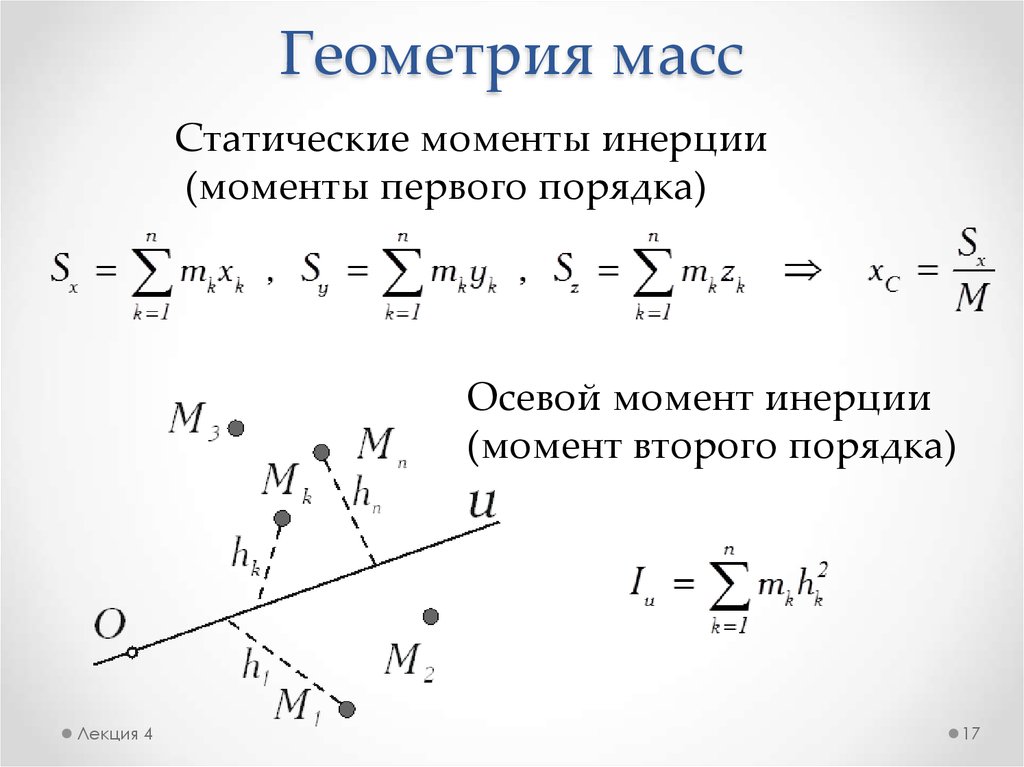
17. Геометрия масс
Статические моменты инерции(моменты первого порядка)
Осевой момент инерции
(момент второго порядка)
Лекция 4
17
18. Моменты второго порядка
ОсевыеЦентробежные
Лекция 4
18
19. Свойства моментов второго порядка
1. Осевой момент невырожденногоположительное число.
тела
есть
Iz 0
2. Сумма моментов инерции относительно двух
любых осей не меньше момента относительно
третьей оси.
Ix Iy Iz
3. Сумма моментов относительно трех осей,
проходящих через одну и ту же точку, не зависит
от направления этих осей
I x I y I z const 2 I O
Лекция 4
19
20. Теорема Гюйгенса – Штейнера
Момент инерции твердого тела относительно выбранной оси равен суммемомента инерции относительно оси, параллельной выбранной и проходящей
через центр масс тела, и произведения массы тела на расстояние между
осями
Лекция 4
20
21.
1.Из моментов инерции относительно
параллельных осей наименьшим будет момент
относительно оси, проходящей через центр масс
тела (центральной оси).
2.
Лекция 4
21
22. Моменты инерции стержня
Лекция 422
23.
Лекция 423














 Физика
Физика








