Динамика механической системы и твердого тела (§12 - §14). Некоторые виды систем

1. Глава 3 Динамика механической системы и твердого тела

§ 12. Некоторые виды систем
12.1. Неизменяемая система
12.2. Система с идеальными связями
12.3. Примеры идеальных связей
§ 13. Дифференциальные уравнения движения твердого
тела
§ 14. Принцип Даламбера для механической системы
14.1. Главный вектор и главный момент сил инерции
системы
14.2. Приведение сил инерции твердого тела
14.3. Динамические реакции, действующие на ось при
вращении тела

2. § 12. Некоторые виды систем

12.1. Неизменяемая система
Неизменяемой называют механическую систему, в
которой расстояние между каждыми двумя
взаимодействующими точками во все время движения
остаётся постоянным
Рассмотрим две точки в неизменяемой системе, т.е.
В1В2 = const
V1
Пусть точка В1 движется со
скоростью V1 ,
α
а точка В2 – со скоростью V2 ,
V2
В1
тогда по теореме о проекциях
F12
β
F21 В2
скоростей V1 cos V2 cos ,
т.к.
ds V dt
, то
ds1 cos ds2 cos

3. следовательно,

A F
F
A F F
i
12
ds1 cos ,
i
12
i
21
i
21
ds2 cos
Сложим эти выражения, воспользовавшись свойством
внутренних сил, тогда имеем
A F
i
12
A F 0,
i
21
и теорема об изменении кинетической энергии для
e
такой системы будет dT
dA F
k
k
или
T1 T0 A Fke
k

4. 12.2. Система с идеальными связями

Рассмотрим систему, на которую наложены связи, не
изменяющиеся со временем
Разделим все внешние и внутренние силы на активные
a
r
и реакции связей, тогда dT
dAk
dAk
k
k
Т.к. силы реакции связи – постоянные, то
r
dA
k 0,
k
и теорема об изменении кинетической энергии для такой
системы запишется
dT dAka
k
Связи называются идеальными, если они не
изменяются со временем и при элементарном
перемещении системы сумма их работ равна нулю

5. 12.3. Примеры идеальных связей

1. Движение по гладкой поверхности
dA Fтр 0
2. Если связью является неподвижная поверхность
(или кривая), трением о которую можно пренебречь
A N 0
3. Качение без скольжения по твердой поверхности
A Fтр 0
4. Качение по абсолютно твердой поверхности (без
деформаций)
A F
0 и A N 0
сопр

6. 5. При нерастяжимых нитях и стержнях

A Fупр 0
6. Шарнирно неподвижная опора
A Rшарн 0 ,
если Fтр = 0
Вывод
В случае системы с идеальными связями теорема об
изменении кинетической энергии
Tкон Tнач A Fka
k
(22)

7. § 13. Дифференциальные уравнения движения твердого тела

1. Если тело двигается поступательно, то
дифференциальное уравнение его движения запишется
как движение центра масс
M aC Fke
(23)
k
в координатном представлении
M xC Fkxe ;
M yC Fkye ;
k
M zC Fkze
k
k
2. Если тело двигается вращательно, то по теореме
dK Z
моментов
momZ Fke . K J , а ,
dt
(24)
Z
Z
k
J Z momZ Fke
k
– дифференциальное
уравнение движения
вращающегося тела

8.

3. Если тело двигается плоско-параллельно, то
положение его центра масс описывает уравнение
движения центра масс системы, а уравнение для
вращательного движения – его вращение относительно
МЦС
M xC Fkxe
k
M yC Fkye
k
M zC Fkze
k
J zC momzC Fke
k
(25)

9. § 14. Принцип Даламбера для механической системы

Для каждой точки системы можем записать уравнение
e
i
ин
принципа Даламбера Fk Fk Fk 0
Просуммируем по всем точкам системы
e
i
ин
F
F
F
k k k 0
(26)
k
Если в любой момент времени к каждой из точек
системы кроме действующих на нее внешних и
внутренних сил присоединить соответствующие
силы инерции, то полученная система сил будет
уравновешенной и к ней можно применить все
уравнения статики

10. Введем обозначения

R ин Fkин
− главный вектор сил инерции,
k
M Оин momО Fkин
k
F 0
i
k
Так как
− главный момент сил инерции
относительно центра О
и
k
i
mom
F
O k 0
, то
k
e
ин
F
R
0
k
k
mom F M
O
k
e
k
ин
O
0
(27) − условия равновесия
механической
системы

11. 14.1. Главный вектор и главный момент сил инерции системы

При поступательном движении
F M a 0
e
k
R M aC
(28)
R M aC
R M aCn
ин
ин
n
k
C
k
ин
M aC Fke
Главный вектор сил инерции
системы равен произведению
массы системы (тела) на
ускорение центра масс и
направлен в противоположную
сторону ускорения
Тангенциальная и нормальная
(центробежная) силы инерции

12. По теореме об изменении кинетического момента

dK O
dK O
e
e
momO Fk momO Fk
0
dt
dt
k
k
M
ин
O
dK O
dt
M
ин
Z
dK Z
dt
(29) − главный момент
сил инерции системы
относительно центра О
− главный момент
сил инерции системы
относительно оси Z

13. 14.2. Приведение сил инерции твердого тела

Систему сил инерции твердого тела можно
заменить одной силой Rин, приложенной в
произвольно выбранном центре О, и парой сил с
моментом, равным МОин.
1. Пусть механическая система движется поступательно,
тогда ak aC
Все силы инерции образуют систему параллельных
сил и имеют равнодействующую, проходящую через
центр масс системы
F ин M aC

14.

2. Пусть механическая система, обладающая
плоскостью симметрии ОХY, движется вращательно
относительно оси ОZ, тогда результирующая сила Rин
и пара сил с моментом МОин будут лежать в
плоскости ОХY
M
ин
Z
dK Z
JZ JZ
dt
здесь ε − угловое ускорение системы

15. 3. Вращение вокруг оси, проходящей через центр масс системы

Если твердое тело совершает такое движение, то
сила R ин 0 , т.к. aC 0, следовательно, система сил
ин
инерции сводится к паре сил с моментом, равным M CZ
4. Плоско-параллельное движение
Если тело имеет плоскость симметрии и движется
параллельно этой плоскости, то равнодействующая сил
инерции лежит в ней и приложена к центру масс тела, а
пара сил имеет момент
ин
M CZ
J CZ
ε − угловое ускорение тела

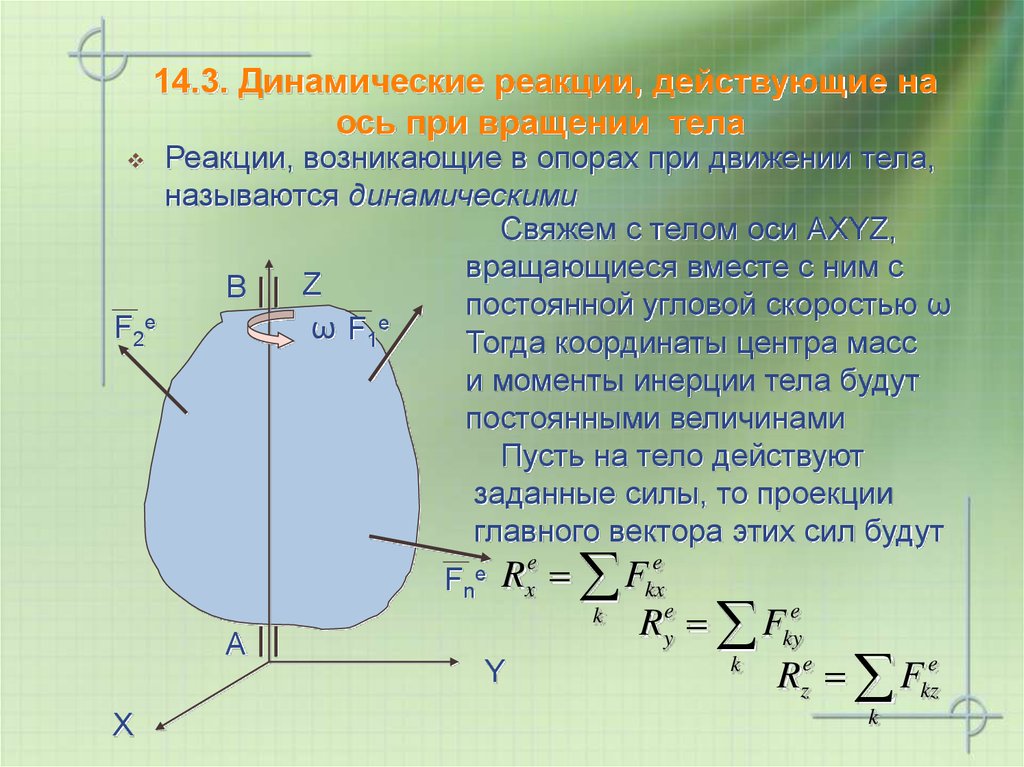
16. 14.3. Динамические реакции, действующие на ось при вращении тела

Реакции, возникающие в опорах при движении тела,
называются динамическими
Свяжем с телом оси АХYZ,
вращающиеся вместе с ним с
Z
B
постоянной угловой скоростью ω
e
e
F2
ω F1
Тогда координаты центра масс
и моменты инерции тела будут
постоянными величинами
Пусть на тело действуют
заданные силы, то проекции
главного вектора этих сил будут
Rxe Fkxe
k
Rye Fkye
k
Y
Rze Fkze
Fne
A
Х
k

17. Главные моменты относительно тех же осей

e
M xe momx Fke , M ye momy Fke , M z 0, т.к. ω = const
k
k
Определим динамические реакции подшипников
XA, YA, ZA, XB, YB
Z YB
Присоединим силы инерции всех
B
ХВ
частей тела, приведя их к центру А
e
ω
F
e
1
F2
Равнодействующая сила Rин и
пара с моментом
М Аин momA Fkин
k
Fn
ZА
ХА
Х
A
МХин
e
M
YА
МYинY
Rин
Проекции этого момента будут
M xин momx Fkин
M
ин
y
čí
z
mom F
k
y
k
ин
k
0, т.к. const

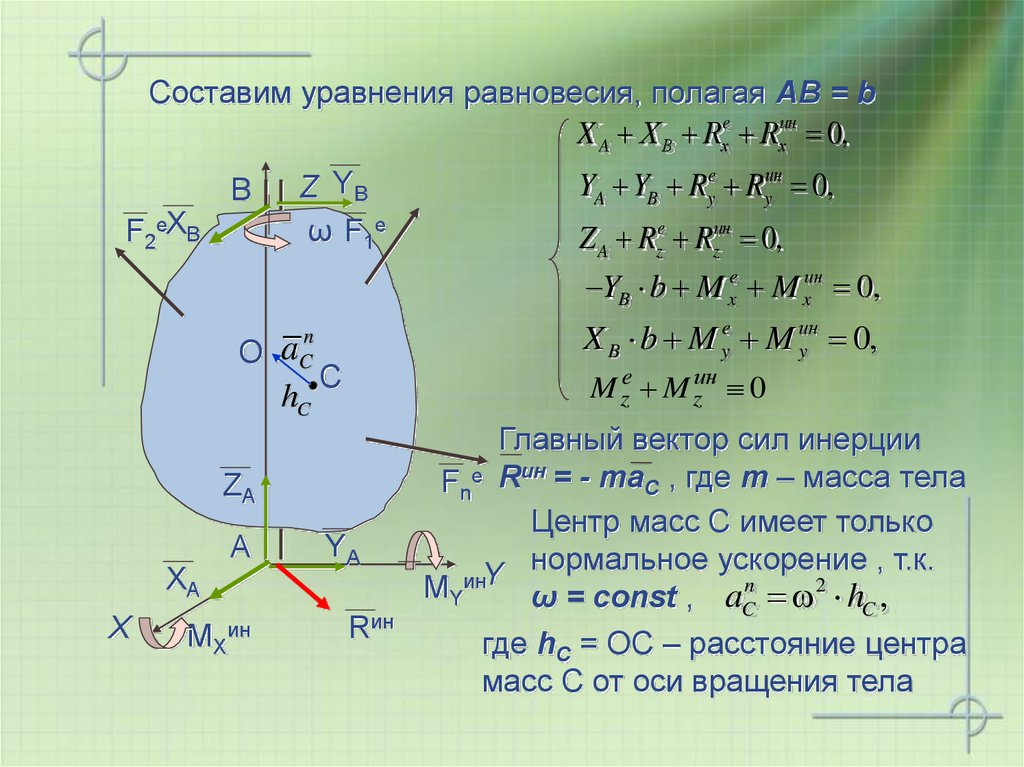
18. Составим уравнения равновесия, полагая АВ = b

X A Х В Rxe Rxин 0,
F2eХВ
Z YB
ω F1e
B
n
C
О a
hC
ХА
Х
МХин
Z A Rze Rzин 0,
YB b M xe M xин 0,
X B b M ye M yин 0,
С
M ze M zин 0
ZА
A
YA YB Rye Ryин 0,
YА
Rин
Главный вектор сил инерции
Fne Rин = - maC , где m – масса тела
Центр масс С имеет только
нормальное ускорение , т.к.
Y
ин
n
2
МY
ω = const , aC hC ,
где hC = ОС – расстояние центра
масс С от оси вращения тела

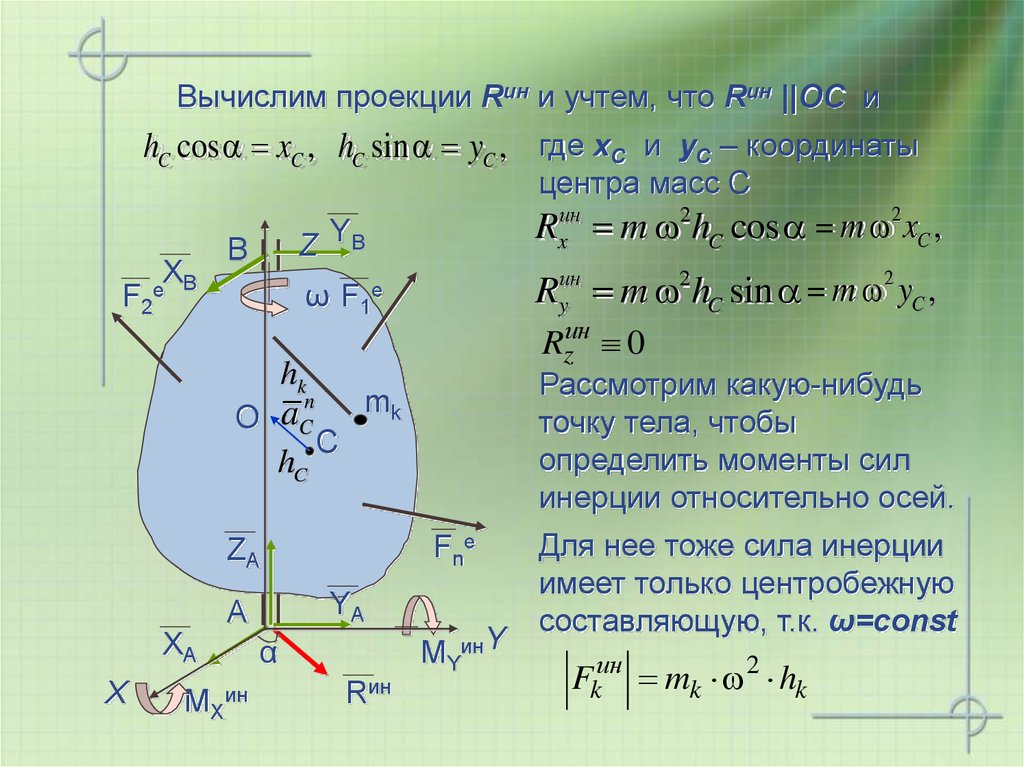
19. Вычислим проекции Rин и учтем, что Rин ||ОС и

hC cos xC , hC sin yC , где xC и yC – координаты
центра масс С
F2
Х
e В
Rxин m 2hC cos m 2 xC ,
Z YB
B
ω F1
hk
n
C
О a
hC
Х
Рассмотрим какую-нибудь
точку тела, чтобы
определить моменты сил
инерции относительно осей.
С
Fne
YА
A
МХин
Rzин 0
mk
ZА
ХА
Ryин m 2hC sin m 2 yC ,
e
МYинY
α
Rин
Для нее тоже сила инерции
имеет только центробежную
составляющую, т.к. ω=const
Fkин mk 2 hk

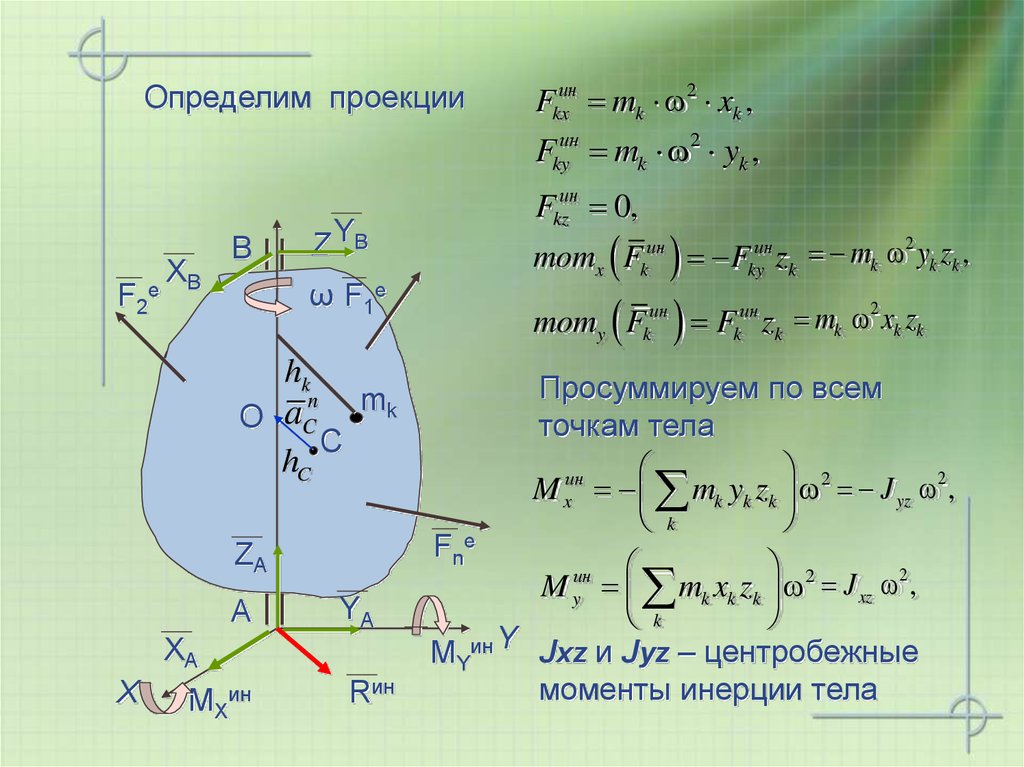
20. Определим проекции

Fkxин mk 2 xk ,
Fkyин mk 2 yk ,
F2
Х
e В
Z YB
B
ω F1e
hk
n
C
О a
hC
mk
С
ZА
A
YА
ХА
Х
МХин
Rин
Fkzин 0,
momx F
F F
ин
k
momy
ин
k
2
m
yk zk ,
F z
k
ин
ky k
2
z mk xk zk
ин
k
k
Просуммируем по всем
точкам тела
M xин mk yk zk 2 J yz 2 ,
k
e
Fn
M yин mk xk zk 2 J xz 2 ,
k
Y
МYин Jxz и Jyz – центробежные
моменты инерции тела

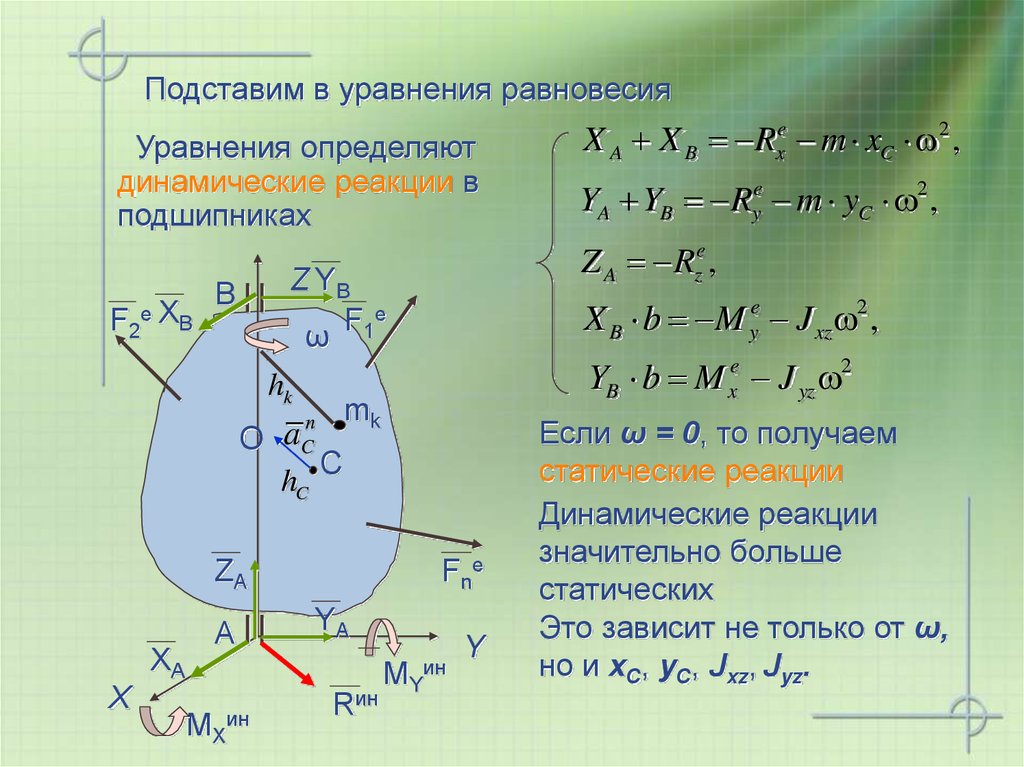
21. Подставим в уравнения равновесия

Уравнения определяют
динамические реакции в
подшипниках
F2e ХВ
hk
n
C
О a
С
hC
Х
ХА
A
МХин
X B b M ye J xz 2 ,
YB b M xe J yz 2
mk
Fne
ZА
YА
Rин
YA YB Rye m yC 2 ,
Z A Rze ,
Z YB
F1e
ω
B
X A X B Rxe m xC 2 ,
МYин
Y
Если ω = 0, то получаем
статические реакции
Динамические реакции
значительно больше
статических
Это зависит не только от ω,
но и хС, уС, Jxz, Jyz.

22. Если хС = 0, yС = 0, Jxz = 0, Jyz = 0, то наличие вращения не влияет на значения реакций подшипников

Получили условие динамической уравновешенности
вращающегося тела относительно оси Z
Динамическое уравновешивание вращающихся тел –
важная техническая задача
Любую ось, проведенную в теле, можно сделать
главной центральной осью инерции, прибавляя к телу
две точечные массы!
Пусть для тела массой m координаты его центра масс
и центробежные моменты инерции известны и не равны
нулю: хС ≠ 0, yС ≠ 0, Jxz ≠ 0, Jyz ≠ 0

23.

Прибавим к телу ещё две массы m1 и m2 в точках с
координатами (х1, у1, z1) и (х2, у2, z2)
Найдем радиус-вектор центра масс такой системы и
её центробежные моменты инерции
1
rC mk rk , Чтобы для полученной системы
M k
ось Z стала главной центральной
J xy mk xk yk , осью инерции, необходимо
k
J yz mk yk zk ,
k
J zx mk zk xk
k
выполнение следующих условий
m xC m1 x1 m2 x2 0,
m yC m1 y1 m2 y2 0,
J xz m1 x1 z1 m2 x2 z2 0,
J yz m1 y1 z1 m2 y2 z2 0
Тогда х’С = 0, y’С = 0, J’xz= 0, J’yz = 0

24. Механический смысл величин

J xz
и
J yz
Центробежные моменты инерции характеризуют
степень динамической неуравновешенности тела при
его вращении вокруг оси Z
ин
M CZ