Похожие презентации:
Введение в динамику системы. Масса. Центр масс. Моменты инерции
1.
ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.ДИНАМИКА
ЛЕКЦИЯ 6
2. Цель лекции
Познакомиться с механической системой и с ееосновными характеристиками и свойствами.
План лекции
Введение
• Механическая система. Силы внутренние и внешние.
• Масса системы. Центр масс
• Момент инерции относительно оси.
• Теорема Гюйгенса
Заключение
2
Цель лекции
3. Механическая система
Совокупность материальных точек,движения которых взаимосвязаны,
называют механической системой.
Твердые тела или системы тел
частный случай механической
системы.
1
2
3
Механическая система
3
1
N
3
2
N
4. Внешние и внутренние силы
СилыВнутренние
4
Внутренние и внешние силы
Внешние
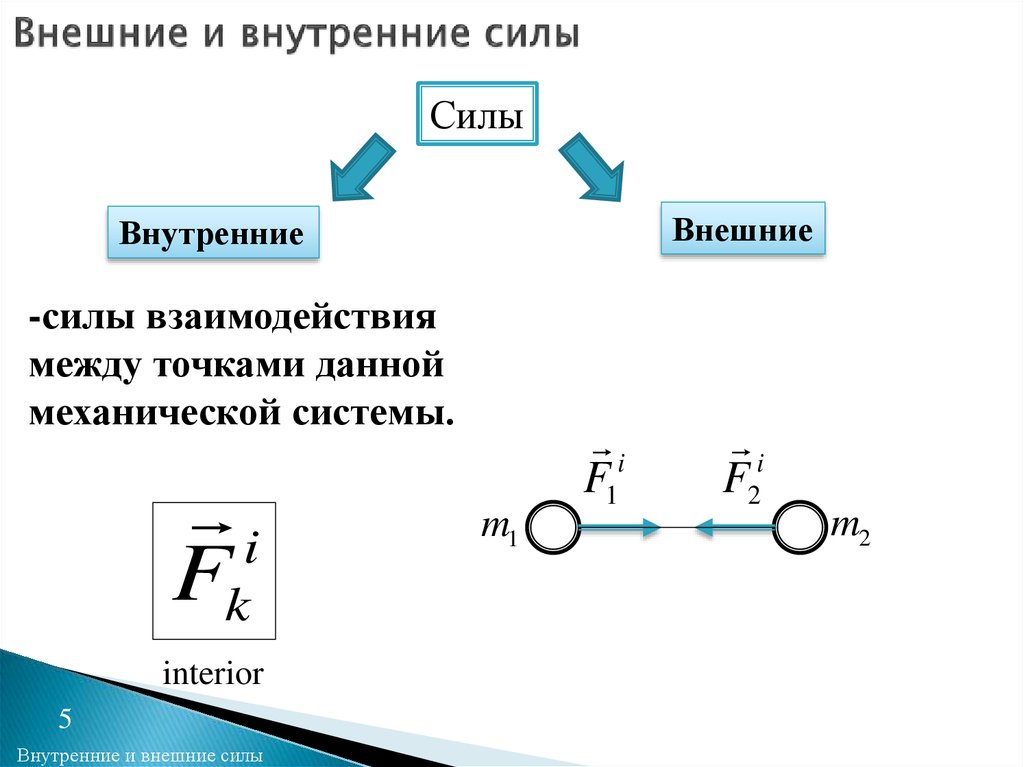
5. Внешние и внутренние силы
СилыВнешние
Внутренние
-силы взаимодействия
между точками данной
механической системы.
i
Fk
interior
5
Внутренние и внешние силы
m1
i
F1
i
F2
m2
6. Свойства внутренних сил
iF21
i
F12
A2
h
O
A1
i
i
F12 F21
i
i
F21 F12
6
Свойства внутренних сил
m (F ) m (F ) 0
1. Геометрическая сумма всех внутренних
i
i
сил, действующих на точки системы,
O
12
O
21
равна нулю.
i i
12Fk
h
F h 0 F 0
i
21
2. Сумма моментов всех внутренних
сил системы относительно любого центра
или оси равняется нулю.
i
mO ( Fk ) 0
i
mx ( Fk ) 0
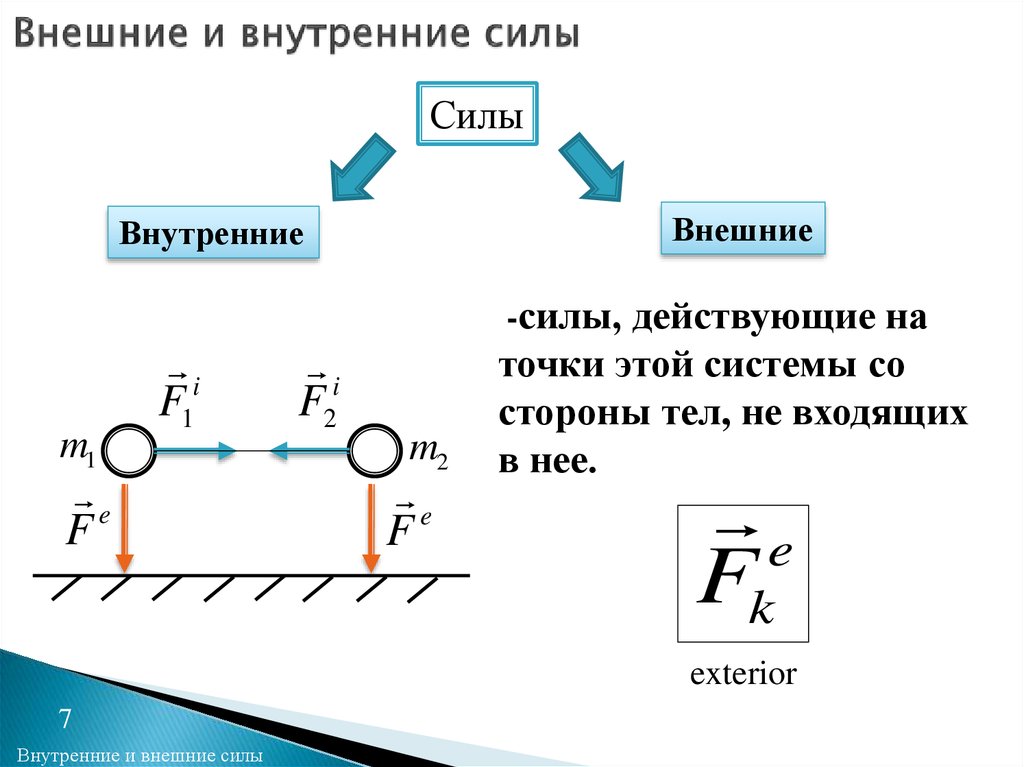
7. Внешние и внутренние силы
СилыВнешние
Внутренние
-силы, действующие на
m1
i
F1
e
F
i
F2
m2
e
F
точки этой системы со
стороны тел, не входящих
в нее.
e
Fk
exterior
7
Внутренние и внешние силы
8.
Внешние и внутренние силыe
F
i
F
8
Активные силы
9.
ХАРАКТЕРИСТИКИ МЕХАНИЧЕСКОЙ СИСТЕМЫЦентр масс
Масса
Момент инерции
9
Характеристики механической
системы
10. МАССА СИСТЕМЫ. ЦЕНТР МАСС
Масса системы равна арифметической сумме массвсех точек или тел образующих систему:
Центроммера
масс инертности
механической
Масса-
системы называется геометрическая
точка С, координаты которой
определяются формулами
xc
m x
k
M
k
yc
m
Масса системы
yk
M
или
10
k
rc
M mk
zc
m z
mk rk
M
k k
M
11.
11Момент инерции
12.
12Центр масс
13. МОМЕНТ ИНЕРЦИИ ОТНОСИТЕЛЬНО ОСИ
zhk
Jz m h
2
k k
mk
Jz m h
2
k k
O
x
y
J z кг м2
Моментом инерции тела (системы)
относительно данной оси Oz называется
величина, равная сумме произведений масс
всех точек тела (системы) на квадраты их
расстояний до этой оси
Момент инерции
14.
МОМЕНТ ИНЕРЦИИ ОТНОСИТЕЛЬНО ОСЕЙz
hk
2
2
2
h
x
y
Зная, что k
k
k
mk
Тогда моменты инерции относительно
осей будут определяться формулами:
y
O
x
yk
xk
J x mk ( zk2 yk2 )
J y mk ( zk2 xk2 )
J z mk ( xk2 yk2 )
14
Момент инерции
15.
МОМЕНТ ИНЕРЦИИ СПЛОШНОГО ТЕЛАJz m h
2
k k
Учитывая, что
dm dV
J z h dm
2
M
15
Момент инерции
J z h dV
2
или
V
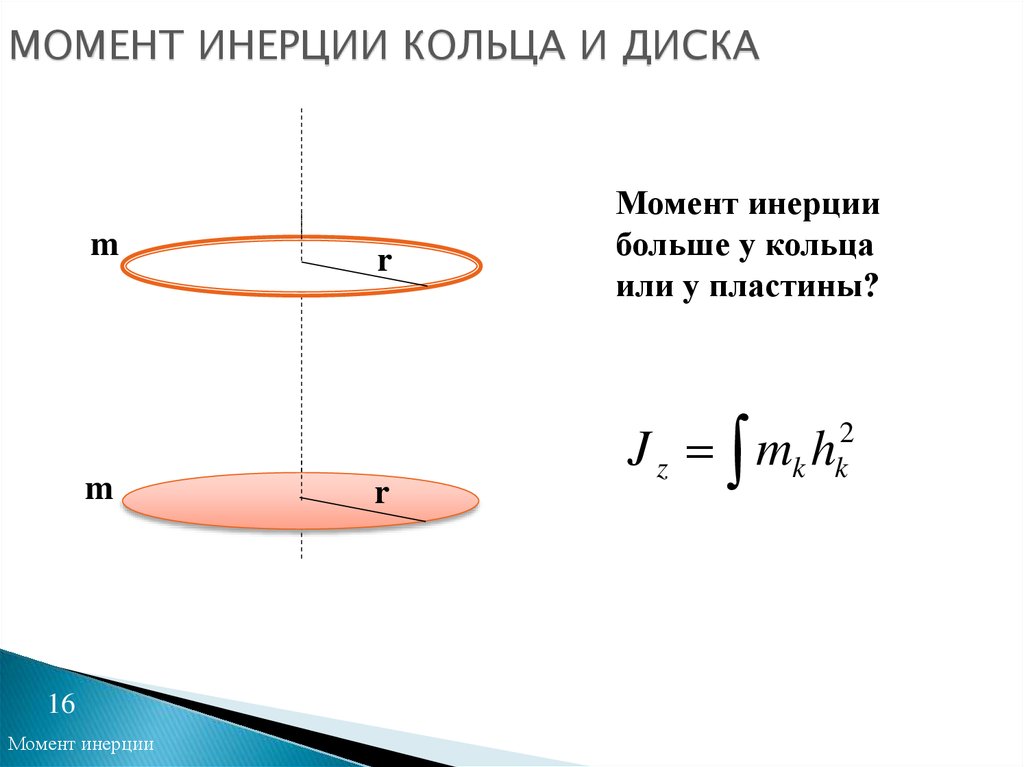
16.
МОМЕНТ ИНЕРЦИИ КОЛЬЦА И ДИСКАm
m
16
Момент инерции
r
r
Момент инерции
больше у кольца
или у пластины?
Jz m h
2
k k
17.
ПРИМЕРЫ МОМЕНТОВ ИНЕРЦИИ ТЕЛ2
J z h dm dm l dl
Тонкий стержень
Дано: m и l
M
y
А
l
J A x 2 dm x 2 l dx x
l
M
h
dm
l
dx
x
13
Момент инерции
3
0
m
, получаем:
Зная l
l
ml
JA
3
3 l
2
0
18.
ПРИМЕРЫ МОМЕНТОВ ИНЕРЦИИ ТЕЛТонкое кольцо:
J A mk R mk R MR
2
J A MR
18
Момент инерции
2
2
2
19.
ПРИМЕРЫ МОМЕНТОВ ИНЕРЦИИ ТЕЛДиск
J Z r 2 dm
M
M
R
r
R
R
0
0
r 2 S 2 rdr 2 S r 3dr
z
M
M
2
dm s dS s
S R
dr
19
Момент инерции
2 r
2 S R 4 MR 2
4
2
MR
Jz
2
2
20.
Моменты инерции относительно параллельных осейz
zc
Jz m x
2
k k
d
m (x
k
kc
d)
2
C
xk c
mk ( x 2 xkc d d )
2
kc
2
xk
xk xk c d
Mxkс mk xkс
20
Теорема Гюйгенса
m x 2d mk xkc Md )
2
k kc
J cz1
2
0
J z J cz1 Md
2
21.
Моменты инерции относительно параллельных осейz
zc
C
x, xc
yk ykc
y
d
J z mk ( x y )
2
k
yc
K
mk ( x 2 xkc d d y )
2
kc
J z mk ( x y
2
kc
21
Теорема Гюйгенса
2
k
2
kc
2
) m d
k
2
2
k
2 mk xkc d
J z J cz1 Md
2
22.
Теорема ГюйгенсаМомент инерции тела относительно данной оси
равен сумее момента инерции относительно оси,
ей параллельной и проходящей через центр масс
тела, и произведениея массы тела на квадрат
расстояния между осями.
J z J cz1 Md
22
Теорема Гюйгенса
2
23. ЦЕНТРОБЕЖНЫЕ МОМЕНТЫ ИНЕРЦИИ
Центробежные моменты инерциипо отношению к осям Ox, Oy, Oz –
величины, определяемые равенствами
J xy mk xk yk , J yz mk yk zk , J zx mk zk xk
Центробежные моменты инерции могут быть
положительными, отрицательными и равными нулю.
J кг м
2
yz
23
Момент инерции
Оси, для которых центробежные моменты
инерции, содержащие в своих индексах их
наименования, равны нулю, называют
главными осями инерции.
24. ГЛАВНЫЕ ОСИ ИНЕРЦИИ
Для однородного тела, имеющего ось симметрии, даннаяось является её главной осью инерции.
z
c
mk zk xk J zx 0, mk yk zk J yz 0
b
B
a O
x
x A xB
d
y
y A yB
z A zB
A
Если однородное тело имеет плоскость симметрии, то
любая ось, перпендикулярная ей является главной осью
инерции.
24
Момент инерции
Докажите!
25. ГЛАВНЫЕ ОСИ ИНЕРЦИИ
Главные оси инерции, проходящиечерез центр масс системы, называют главными
центральными осями инерции
Динамические реакции, действующие на ось вращающегося
тела, будут равны статическим, если ось вращения, является
одной из главных центральных осей инерции.
25
Момент инерции
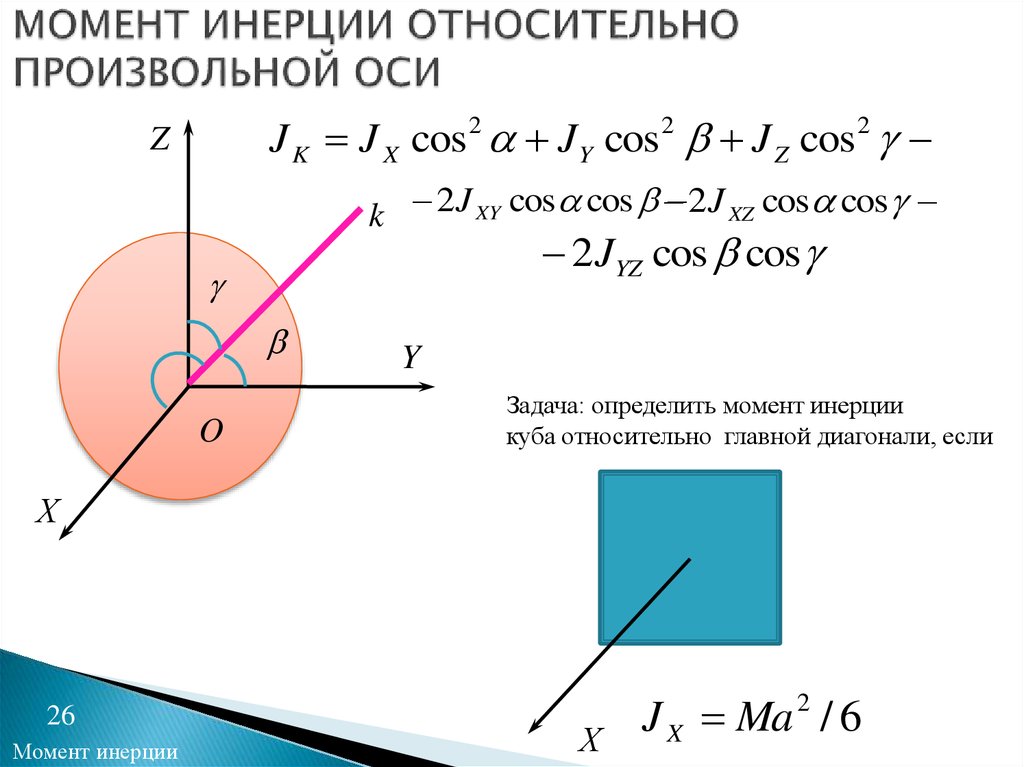
26. МОМЕНТ ИНЕРЦИИ ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ОСИ
J K J X cos 2 J Y cos 2 J Z cos 2Z
k 2J XY cos cos 2J XZ cos cos
2JYZ cos cos
O
Y
Задача: определить момент инерции
куба относительно главной диагонали, если
Х
26
Момент инерции
J X Ma / 6
2
Х
27. ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Каким образом задача о движении произвольноймеханической системы (конструкции) приближенно
сводится к задаче о движении конечного числа
материальных точек?
2. Каковы основные сложности решения системы ДУ
движения N материальных точек? Каков другой путь
приближенного описания движения механических
систем?
3. Какие силы называются внутренними, а какие
внешними?
4. Какими свойствами обладают внутренние силы?
5. Что называют центром масс системы? Как определяются
его координаты?
27
Заключение
28. ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
7. Какова связь между центром масс и центром тяжестисистемы?
8. Как определяется момент инерции тела относительно
оси?
9. Какова зависимость между моментами инерции
относительно двух параллельных осей?
10. Относительно какой из параллельных осей момент
инерции будет наименьшим?
28
Заключение
29. ТЕМА СЛЕДУЮЩЕЙ ЛЕКЦИИ
ТЕОРЕМЫ О ДВИЖЕНИИЦЕНТРА МАСС И ИМПУЛЬСА
29
Заключение























 Физика
Физика








