Похожие презентации:
Объемы прямой призмы и цилиндра. (ЕГЭ. Задачи В10, В1)
1. Объемы прямой призмы и цилиндра ЕГЭ. Задачи В10, В13.
Курылева С.С., учитель математикиМОУ «Лицей №1» г. Воркуты
2. Эпиграф:
ЭПИГРАФ:Первое условие, которое надлежит
выполнять в математике, –
это быть точным, второе – быть
ясным и, насколько можно,
простым.
Лазар Карно
(французский государственный и военный
деятель, инженер и ученый)
3. задачи на урок:
повторить формулы для вычисленияобъема прямой призмы и цилиндра;
учиться применять формулы для
вычисления объема прямой призмы и
цилиндра при решении задач;
рассмотреть задачи на вычисление
объема призмы, вписанной в цилиндр и
призмы, описанной около цилиндра.
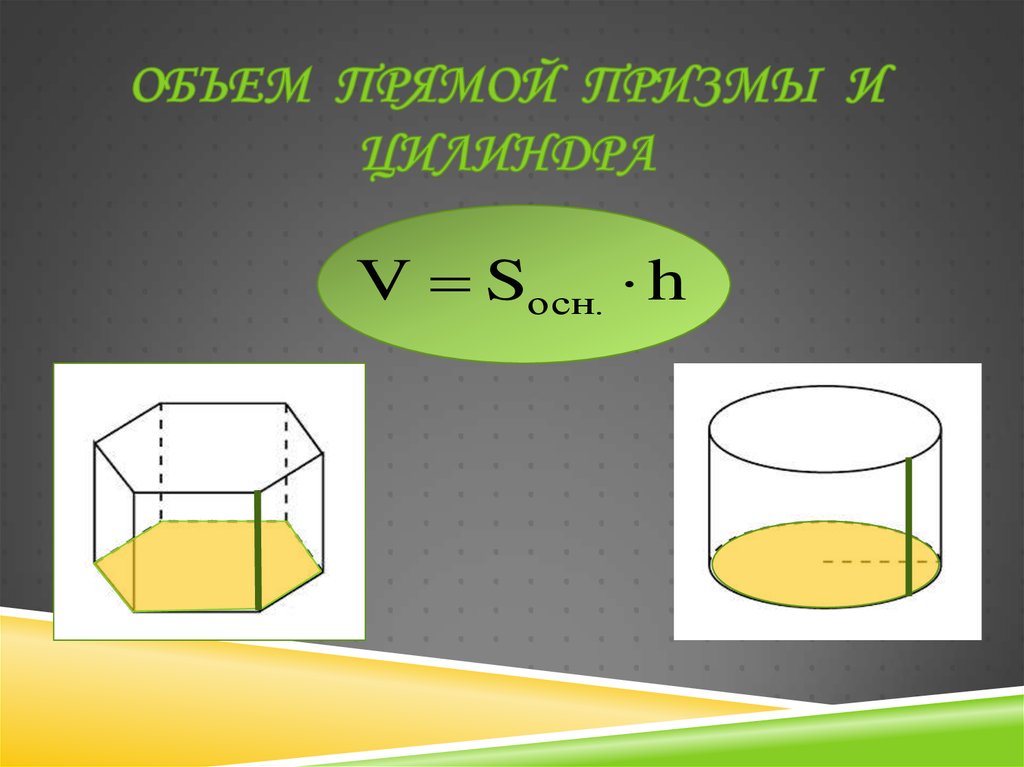
4. Объем ПРЯМОЙ призмы И ЦИЛИНДРА
V Sосн. h5. СВЕДЕНИЯ ИЗ ПЛАНИМЕТРИИ
6.
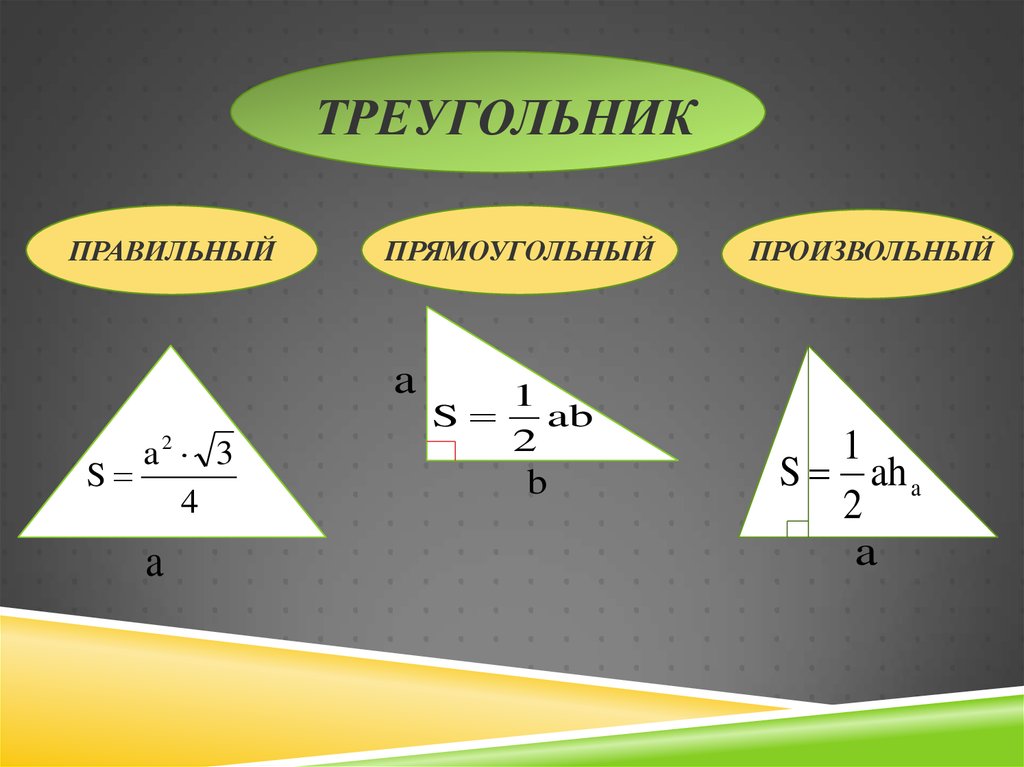
ТРЕУГОЛЬНИКПРАВИЛЬНЫЙ
ПРЯМОУГОЛЬНЫЙ
a
a2 3
S
4
a
S
1
ab
2
b
ПРОИЗВОЛЬНЫЙ
1
S ah a
2
a
7.
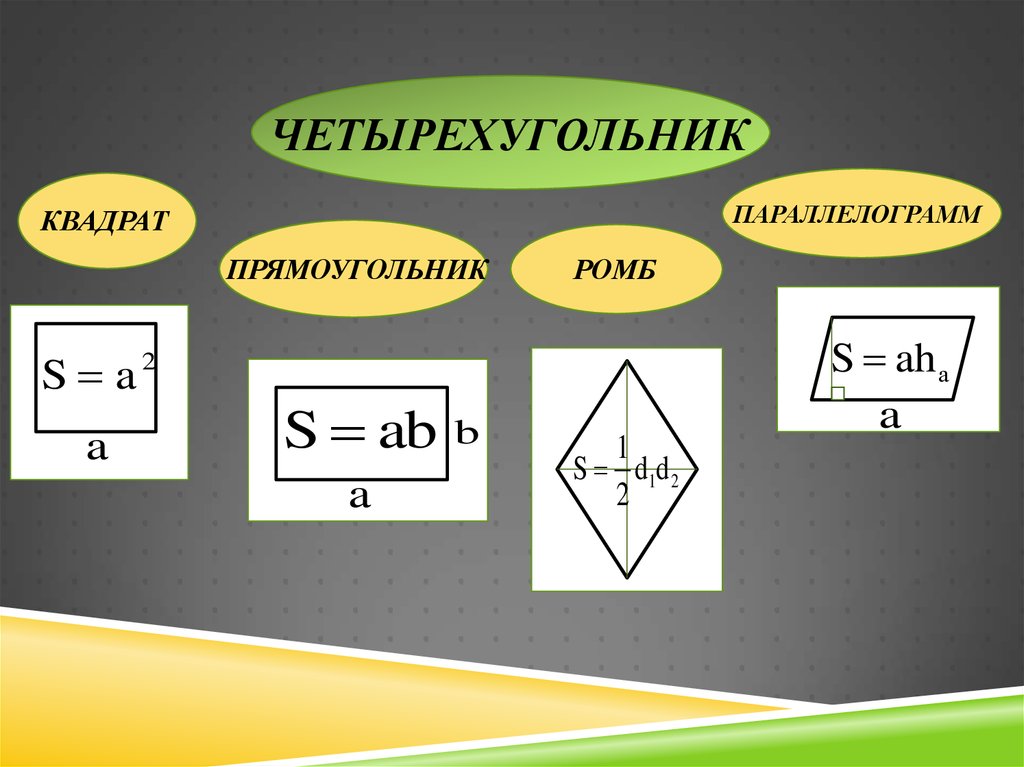
ЧЕТЫРЕХУГОЛЬНИКПАРАЛЛЕЛОГРАММ
КВАДРАТ
ПРЯМОУГОЛЬНИК
S a
a
РОМБ
2
S ab
a
b
1
S d1d 2
2
S ah а
a
8.
ПРАВИЛЬНЫЙ ШЕСТИУГОЛЬНИК3 3a 2
S
2
а
9.
ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯРАДИУСА ВПИСАННОЙ И ОПИСАННОЙ
ОКРУЖНОСТИ
Правильный треугольник
r
a
3
6
, R
a
3
3
a b c
1
,
R
с, где с гипотенуза
Прямоугольный треугольник
2
2
a
r
, R a 2
Квадрат
2
2
1
R
d, где d диагональ
Прямоугольник
2
r
Правильный шестиугольник
r
a 3
,
2
R а
10. Некоторые отношения подобия
НЕКОТОРЫЕ ОТНОШЕНИЯПОДОБИЯ
• Отношение периметров подобных
многоугольников равно коэффициенту
подобия.
• Отношение площадей подобных фигур
равно квадрату коэффициента подобия.
• Отношение объемов подобных тел
равно кубу коэффициента подобия.
11. ОБЪЕМ ПРИЗМЫ
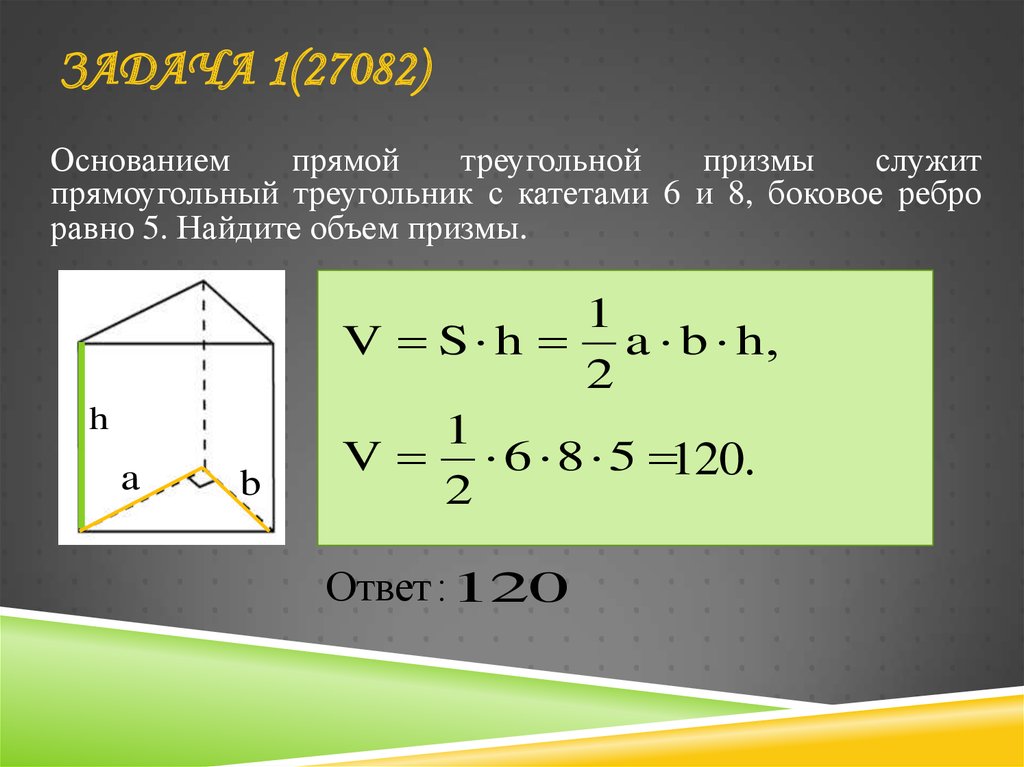
12. ЗАДАЧА 1(27082)
Основаниемпрямой
треугольной
призмы
служит
прямоугольный треугольник с катетами 6 и 8, боковое ребро
равно 5. Найдите объем призмы.
h
a
b
1
V S h a b h,
2
1
V 6 8 5 120.
2
Ответ : 120
13. ЗАДАЧА 2(27084)
Найдите объем правильной шестиугольной призмы, стороныоснования которой равны 1, а боковые ребра равны √3.
2
h
a
3 3a
V S h
h,
2
3 3 12
V
3 4,5.
2
Ответ : 4,5
14. ЗАДАЧА 3 (27048)
В сосуд, имеющий форму правильной треугольной призмы,налили воду. Уровень воды достигает 80 см. На какой высоте
будет находиться уровень воды, если ее перелить в другой
такой же сосуд, у которого сторона основания в 4 раза больше,
чем у первого? Ответ выразите в см.
а 2 4а1 S2 16S1 ,
1
Так как V1 V2 , то h 2
h1 ,
16
h1
h2
80 :16 5.
Ответ : 5
15. ЗАДАЧА 4 (27047)
В сосуд, имеющий форму правильной треугольной призмы,налили 2300 см³ воды и полностью в нее погрузили деталь. При
этом уровень жидкости в сосуде поднялся с отметки 25 см до
отметки 27 см. Чему равен объем детали? Ответ выразите в см³.
h2
h1
Vводы 2300
Sосн.
92,
h1
25
Vдетали Sосн. h 2 ,
Vдетали 92 27 25 184.
Ответ : 184
16. ОБЪЕМ цилиндра
17. ЗАДАЧА 5(27091)
В цилиндрический сосуд, в котором находится 6 литров воды,опущена деталь. При этом уровень жидкости в сосуде
поднялся в 1,5 раза. Чему равен объем детали? Ответ выразите
в литрах.
h 2 1,5h1 V2 1,5V1 ,
V2 1,5 6 9,
h2
h1
Значит, Vдетали 9 6 3.
Ответ :
3
18. ЗАДАЧА 6(27053)
Объем первого цилиндра равен 12 м3. У второго цилиндравысота в три раза больше, а радиус основания — в два раза
меньше, чем у первого. Найдите объем второго цилиндра.
Ответ дайте в кубических метрах.
Vцилиндра R h,
2
V1 R h1 ,
2
2
1
2
1
R
3
2
R1
3h1 R 1 h1 ,
V2
3h1
4
4
2
3
3
V2 V1 12 9.
4
4
Ответ :
9
19. ЗАДАЧА 7(27199)
Найдите объем V части цилиндра, изображенной на рисунке. Вответе укажите V/π.
Vцил. R 2 h, V 225 5 1125 ,
5
1
5
0
0
60 это
от 360 , 300 это
от 3600
6
6
0
1125 5
V
937,5 .
6
Ответ : 937,5
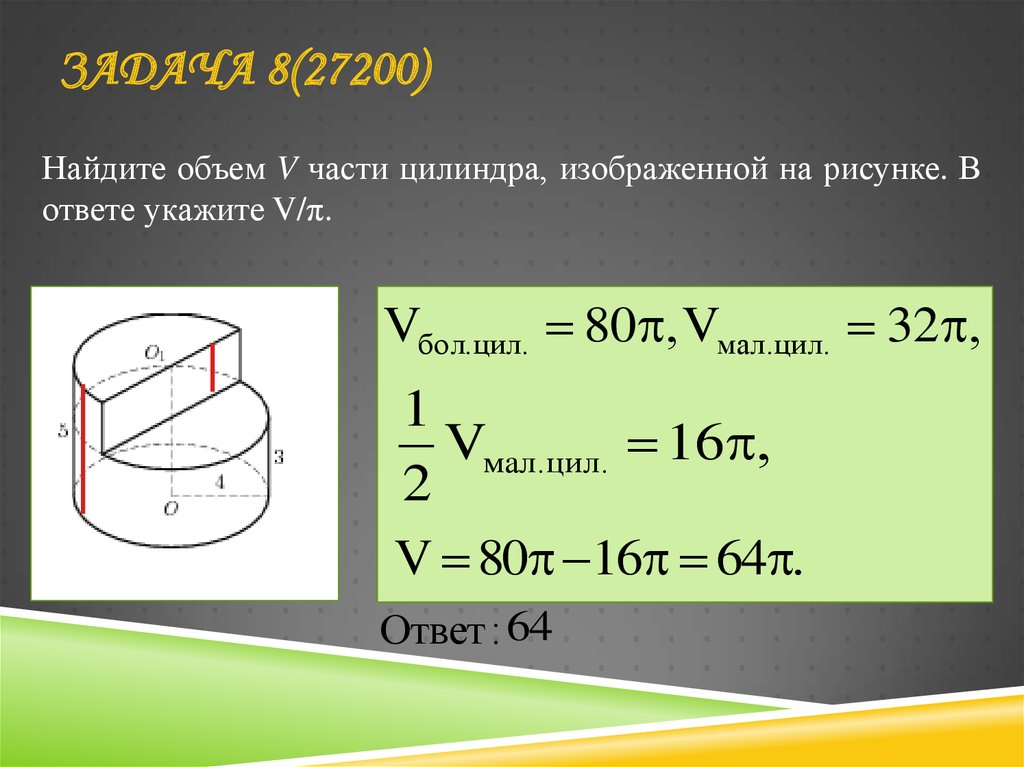
20. ЗАДАЧА 8(27200)
Найдите объем V части цилиндра, изображенной на рисунке. Вответе укажите V/π.
Vбол.цил. 80 , Vмал.цил. 32 ,
1
Vмал.цил. 16 ,
2
V 80 16 64 .
Ответ : 64
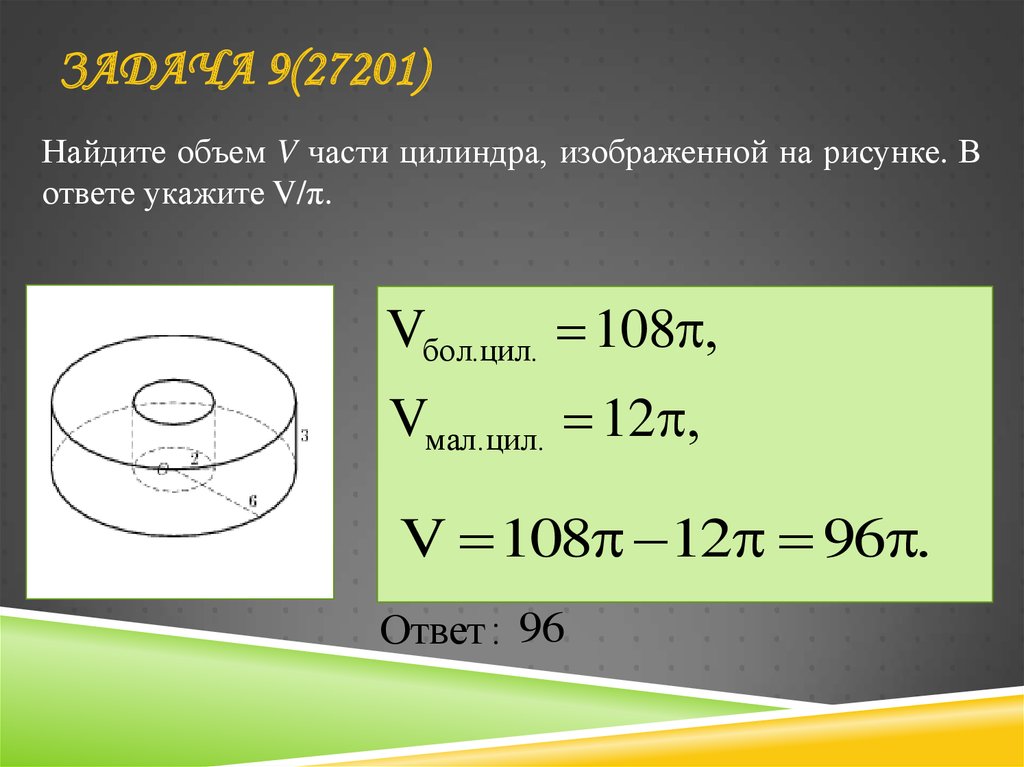
21. ЗАДАЧА 9(27201)
Найдите объем V части цилиндра, изображенной на рисунке. Вответе укажите V/π.
Vбол.цил. 108 ,
Vмал.цил. 12 ,
V 108 12 96 .
Ответ : 96
22. Конфигурации тел
23. Призма, вписанная в цилиндр
ПРИЗМА, ВПИСАННАЯ ВЦИЛИНДР
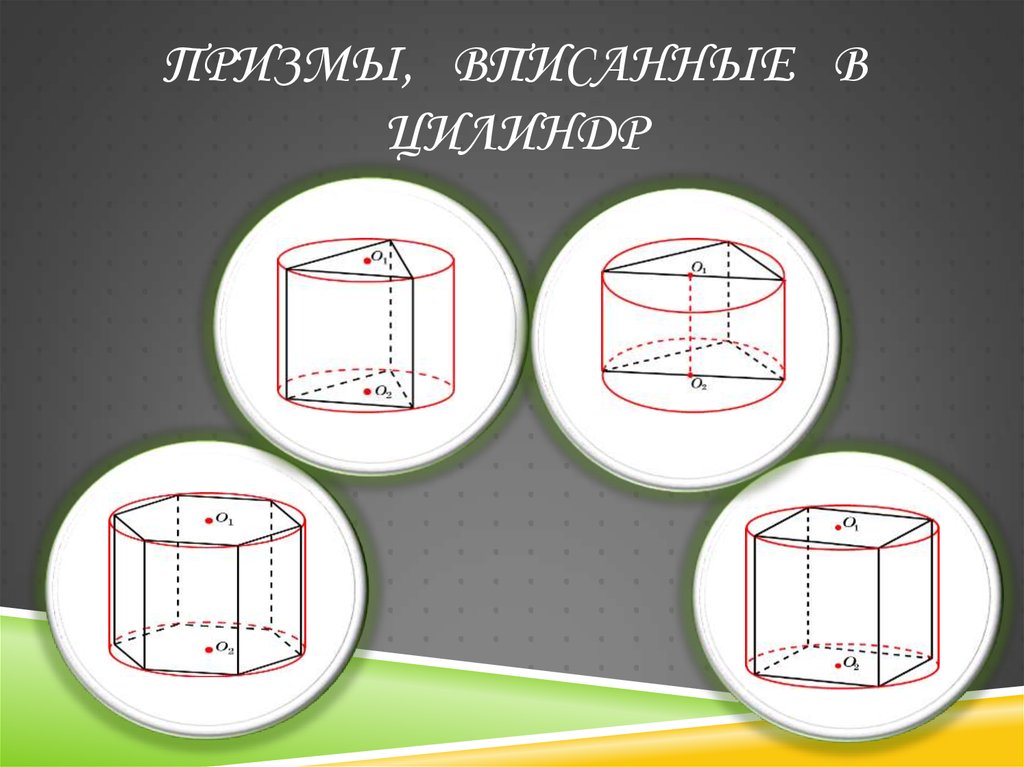
24. Призмы, вписанные в цилиндр
ПРИЗМЫ, ВПИСАННЫЕ ВЦИЛИНДР
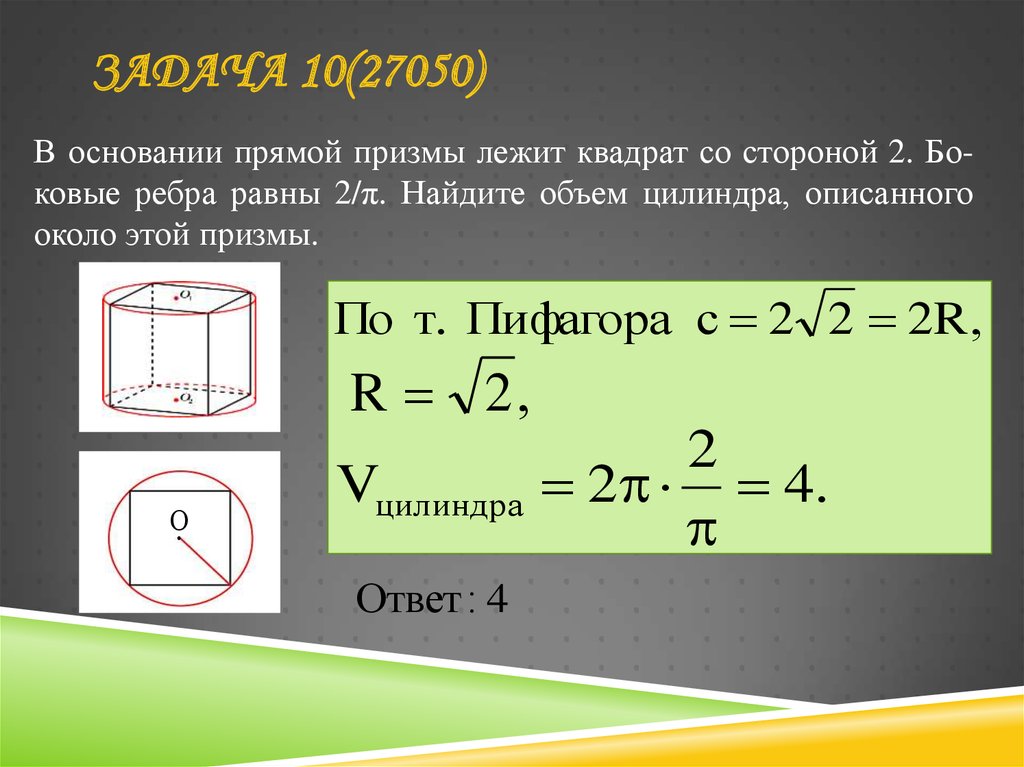
25. ЗАДАЧА 10(27050)
В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны 2/π. Найдите объем цилиндра, описанногооколо этой призмы.
По т. Пифагора с 2 2 2R ,
R 2,
О
Vцилиндра
Ответ : 4
2
2 4.
26. Призма, описанная около цилиндра
ПРИЗМА, ОПИСАННАЯ ОКОЛОЦИЛИНДРА
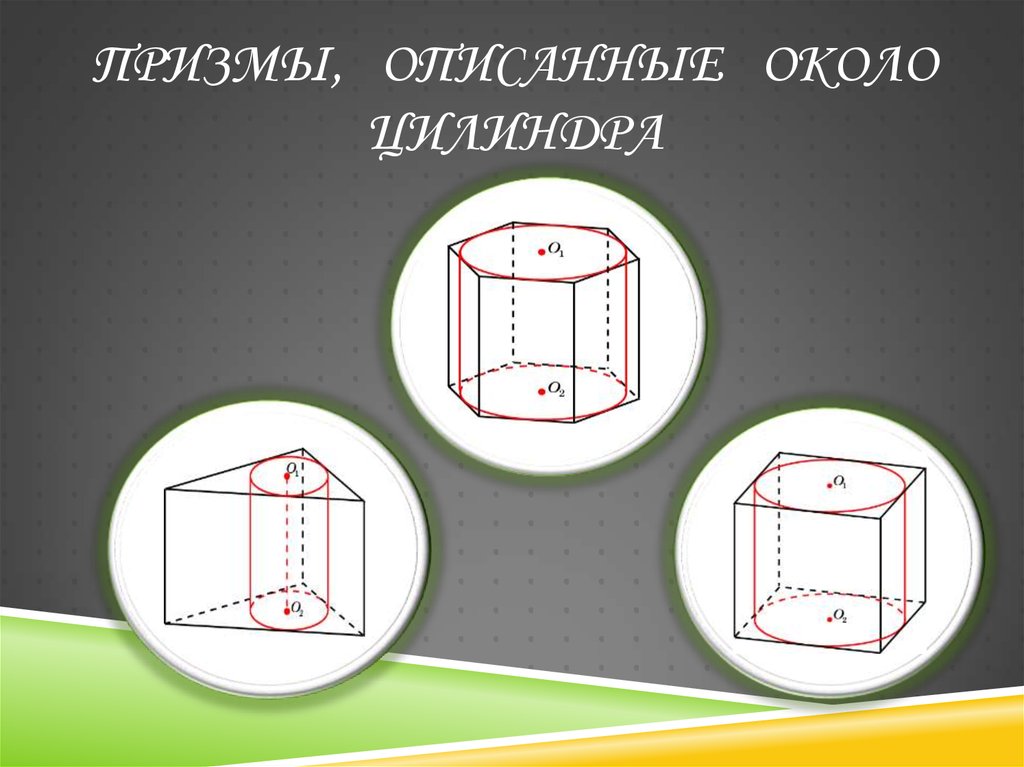
27. Призмы, описанные около цилиндра
ПРИЗМЫ, ОПИСАННЫЕ ОКОЛОЦИЛИНДРА
28. ЗАДАЧА 11(27041)
Правильная четырехугольная призма описана около цилиндра,радиус основания и высота которого равны 1,5. Найдите объем
призмы.
Vпризмы Sосн. h а h,
2
а 2r 1 1,5 3,
Vпризмы 3 1,5 13,5.
2
О
Ответ : 13,5
29. Дополнительная задача
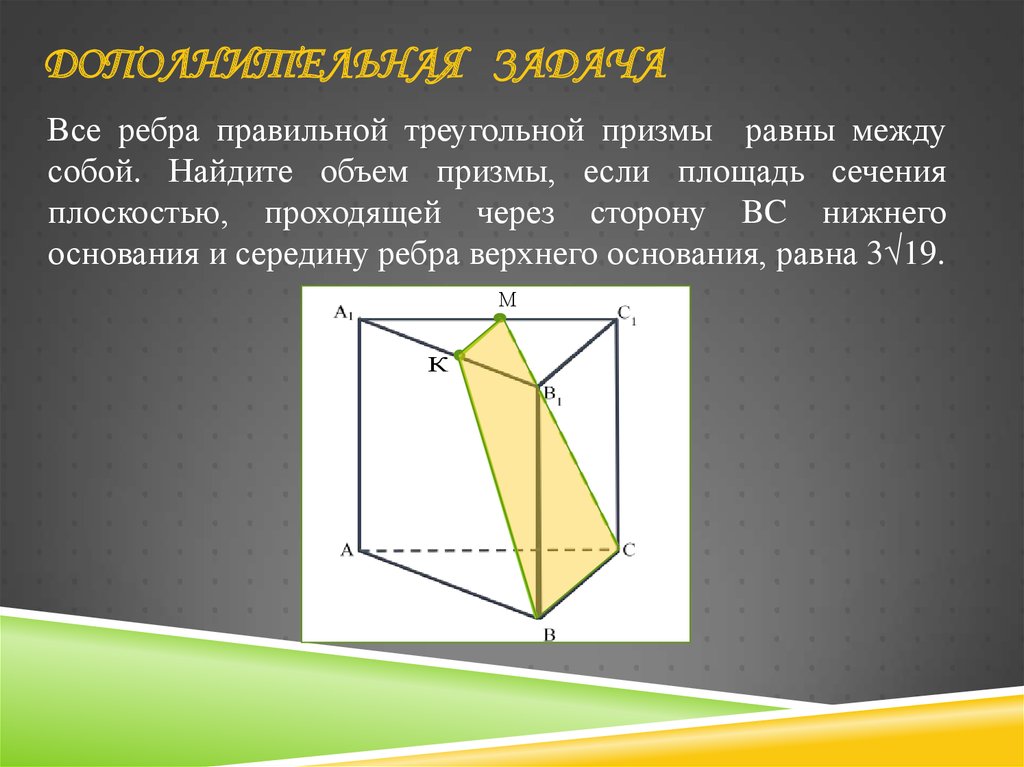
ДОПОЛНИТЕЛЬНАЯ ЗАДАЧАВсе ребра правильной треугольной призмы равны между
собой. Найдите объем призмы, если площадь сечения
плоскостью, проходящей через сторону BC нижнего
основания и середину ребра верхнего основания, равна 3√19.
М
К
30. План решения:
ПЛАН РЕШЕНИЯ:• Строим сечение
• Доказываем, что сечение является
равнобедренной трапецией
• Выполняем рисунок трапеции в плоскости
• Решая планиметрическую задачу, находим
длину стороны а
• Находим объём призмы
:
a3 3
V
4
31. Ответы к самостоятельной работе
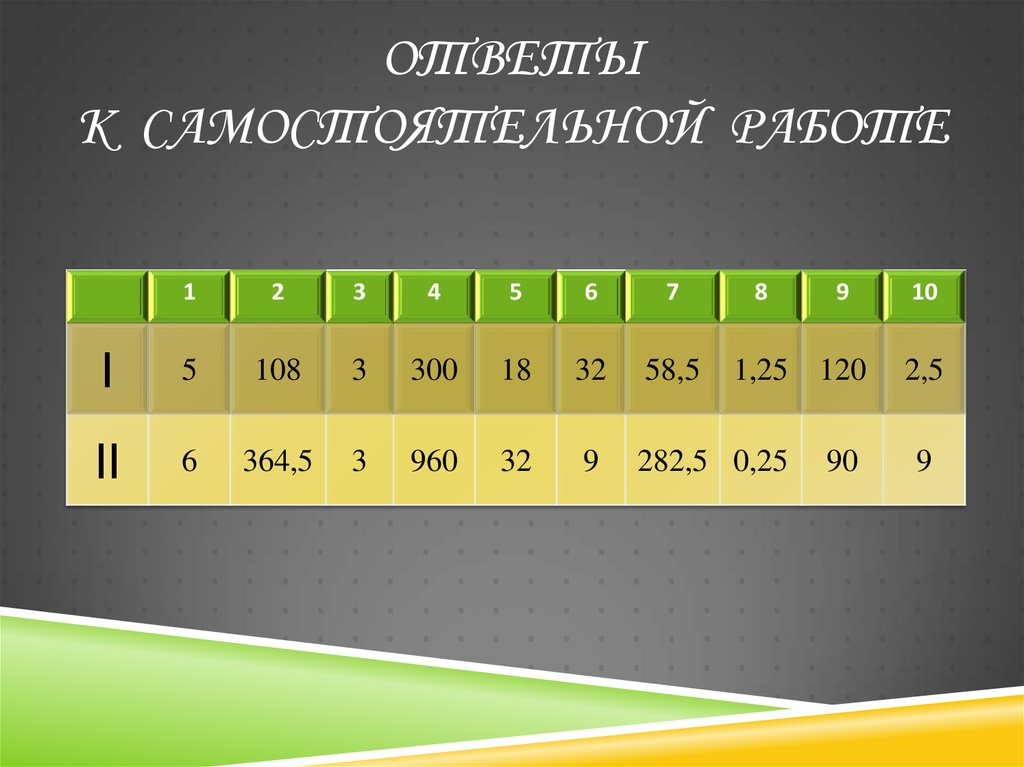
ОТВЕТЫК САМОСТОЯТЕЛЬНОЙ РАБОТЕ
1
2
3
4
5
6
7
8
I
5
108
3
300
18
32
58,5
II
6
364,5
3
960
32
9
282,5 0,25
9
1,25 120
90
10
2,5
9
32.
Учусь решать задачи группы СЗнаю теорию, умею решать
задачи группы В
Умею решать задачи, пользуясь
справочным материалом
Знаю теорию, но не всегда
могу её применить
Не знаю теорию, не умею её
применять






















 Математика
Математика








