Предмет, задачи и метод начертательной геометрии

1.

Лекция 1
1.Предмет, задачи и метод начертательной геометрии
2.Прямоугольные проекции и координаты точек. Эпюр (чертеж)
Г.Монжа. Изображение проекций точек при различном их
положении в пространстве.
3.Изображение прямой линии в ортогональных проекциях.
Взаимное положение точки и прямой. Прямые общего и частного
положения. Следы прямой.
4.Взаимное положение прямых. Понятие конкурирующих точек.
5.Задание плоскости в ортогональных проекциях. Следы
плоскости.
6.Прямые и точки в плоскости.
7.Главные линии плоскости.
8.Плоскости частного положения.
9.Изображение простых поверхностей.

2. 1. Предмет, задачи и метод начертательной геометрии

Начертательная геометрия - это наука изучающая
методы изображения реальных пространственных
объектов.
Метод начертательной геометрии – метод проекций.
Список рекомендованной литературы
Климухин А.Г. Начертательная геометрия.-М,: 1978.
Короев Ю.И. Начертательная геометрия. – М.: 2007.

3.

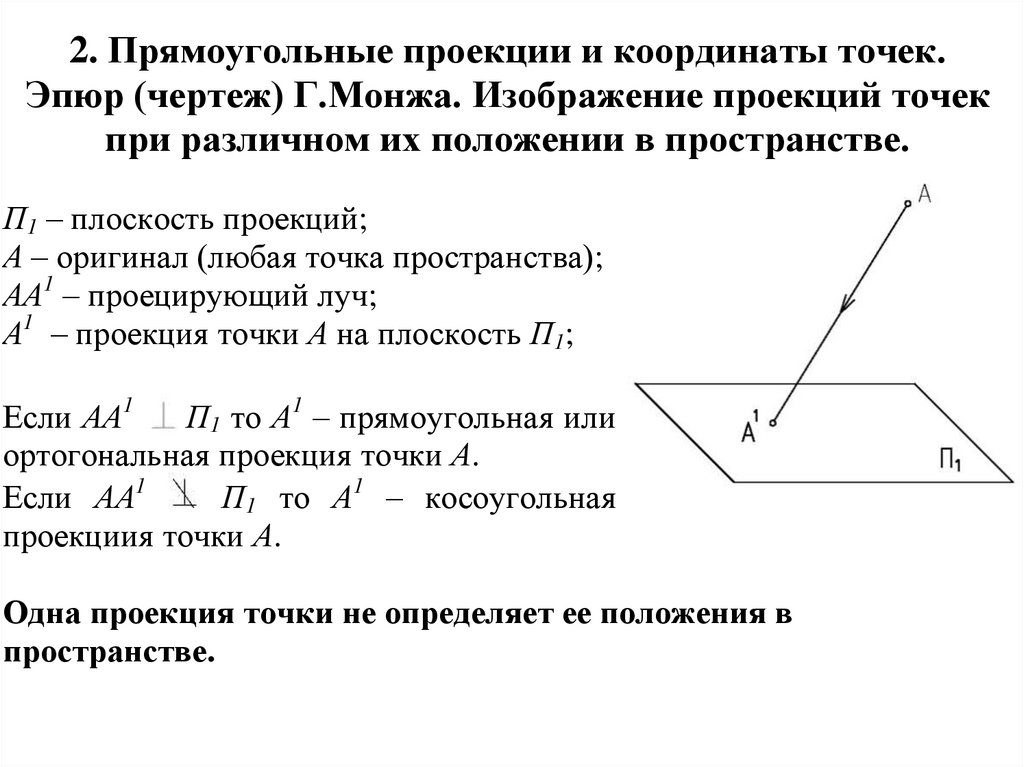
2. Прямоугольные проекции и координаты точек.
Эпюр (чертеж) Г.Монжа. Изображение проекций точек
при различном их положении в пространстве.
П1 – плоскость проекций;
А – оригинал (любая точка пространства);
АА1 – проецирующий луч;
А1 – проекция точки А на плоскость П1;
Если АА1
П1 то А1 – прямоугольная или
ортогональная проекция точки А.
Если АА1
П1 то А1 – косоугольная
проекциия точки А.
Одна проекция точки не определяет ее положения в
пространстве.

4.

П1 – горизонтальная плоскость проекции;
П2 – фронтальная плоскость проекций;
П3 – профильная плоскость проекций.
А1 – горизонтальная проекция точки А;
А2 – фронтальная проекция точки А;
А3 – профильная проекция точки А.
Точка А и ее проекции определяться
координатами:
А (xА; yА; zА) А1 (xА; yА); А2 (xА; zА); А3
(yА; zА);
Две проекции точки полностью
определяют положение точки в
пространстве, так как содержат все
три координаты.
Для перехода от пространственного чертежа к плоскому, плоскость
П1 повернем вокруг оси х12 до совмещения с плоскостью П2.

5.

Плоский чертеж состоящий из горизонтальной
А1 и фронтальной А2 проекций точки А,
расположенных
на
линии
связи
А1А2
перпендикулярной оси x12 называется эпюром
(ортогональным чертежом) и носит имя
основателя начертательной геометрии Г.Монжа.
Линия А1А2 – линия связи проекций А1 и А2.
Построение
профильной
проекции А3 по двум заданным.
k123

6.

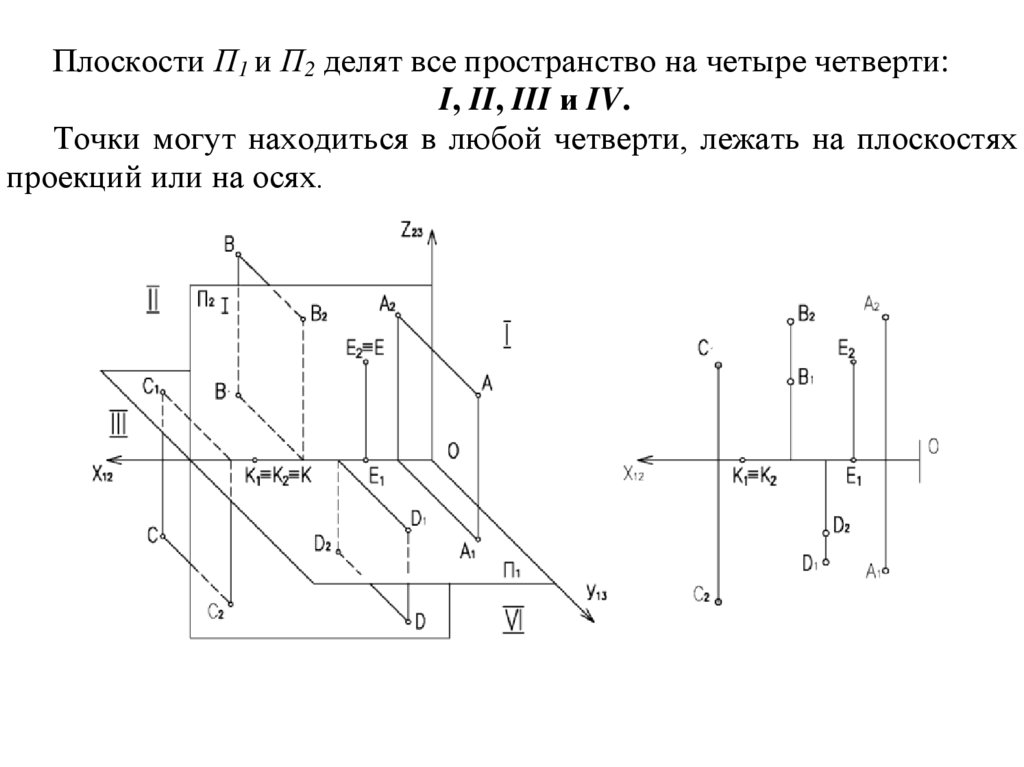
Плоскости П1 и П2 делят все пространство на четыре четверти:
I, II, III и IV.
Точки могут находиться в любой четверти, лежать на плоскостях
проекций или на осях.

7.

3. Изображение прямой линии в ортогональных
проекциях. Взаимное положение точки и прямой.
Прямые общего и частного положения. Следы прямой.
Положение прямой линии в пространстве определяется двумя
ее точками.
Если точка С лежит на прямой, то ее проекции лежат на
соответствующих проекциях прямой.

8.

Прямая, не параллельная ни одной из плоскостей проекций,
называется прямой общего положения.
Длина проекции отрезка прямой общего положения всегда
меньше длины самого отрезка.
Прямые частного положения
Прямые параллельные или перпендикулярные
плоскостям проекций называются прямыми частного
положения

9.

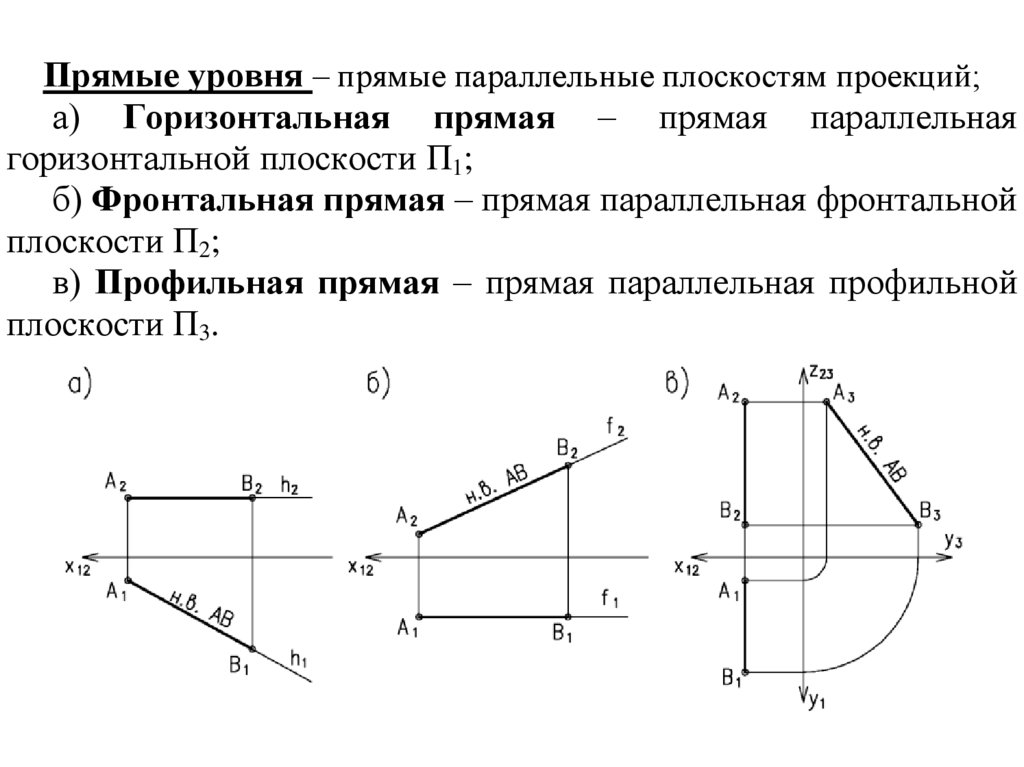
Прямые уровня – прямые параллельные плоскостям проекций;
а) Горизонтальная прямая – прямая параллельная
горизонтальной плоскости П1;
б) Фронтальная прямая – прямая параллельная фронтальной
плоскости П2;
в) Профильная прямая – прямая параллельная профильной
плоскости П3.

10.

Проецирующие
прямые
–
прямые
перпендикулярные
плоскостям проекций.
а) горизонтально-проецирующая прямая – прямая
перпендикулярная горизонтальной плоскости проекций П1;
б)
фронтально-проецирующая
прямая
–
прямая
перпендикулярная фронтальной плоскости проекций П2;
в)
профильно-проецирующая
прямая
–
прямая
перпендикулярная профильной плоскости проекций П3.

11.

Следы прямой на плоскостях
проекций
Следами
прямой
АB
называются точки пересечения ее
с плоскостями проекций.
Точка Н – горизонтальный
след прямой АВ.
Точка F – фронтальный след
прямой АВ.

12.

4. Взаимное положение прямых.
Понятие конкурирующих точек.
Две прямые линии в пространстве могут быть параллельными,
пересекающимися и скрещивающимися.
Если в пространстве две прямые параллельны, то их
одноименные проекции также параллельны.

13.

Пересекающиеся прямые – это прямые,
имеющие общую точку, следовательно, если
прямые в пространстве пересекаются, то точки
пересечения их одноименных проекций лежат на
одной линии проекционной связи.
Скрещивающиеся прямые не имеют
общей точки, поэтому точки пересечения их
одноименных проекций не лежат на одной
линии проекционной связи (рис.14).
Пары точек, у которых какие-либо
одноименные проекции совпали,
называются конкурирующими

14.

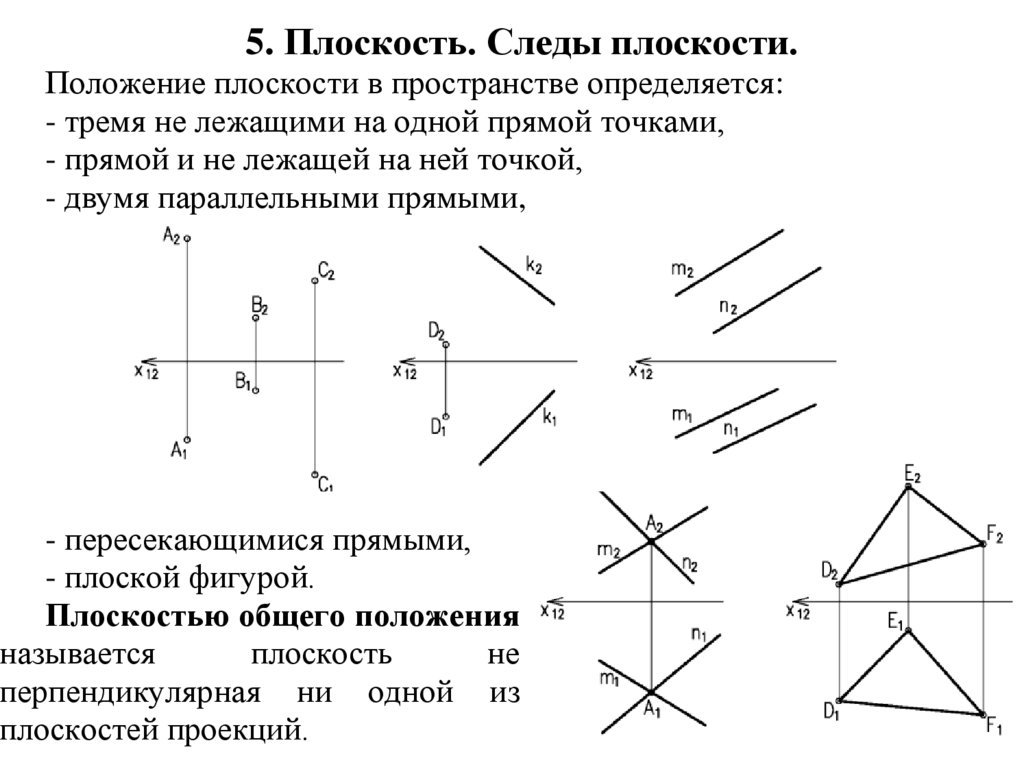
5. Плоскость. Следы плоскости.
Положение плоскости в пространстве определяется:
- тремя не лежащими на одной прямой точками,
- прямой и не лежащей на ней точкой,
- двумя параллельными прямыми,
- пересекающимися прямыми,
- плоской фигурой.
Плоскостью общего положения
называется
плоскость
не
перпендикулярная ни одной из
плоскостей проекций.

15.

Следами плоскости называются линии пересечения плоскости с
плоскостями проекций.
Фронтальным следом плоскости ά называется линия ее
пересечения с фронтальной плоскостью проекций П2 - f ά ( f1ά, f2ά)
Горизонтальный след плоскости ά – линия пересечения с
горизонтальной плоскостью проекций П1 - hά (h1ά, h2ά,)

16.

17.

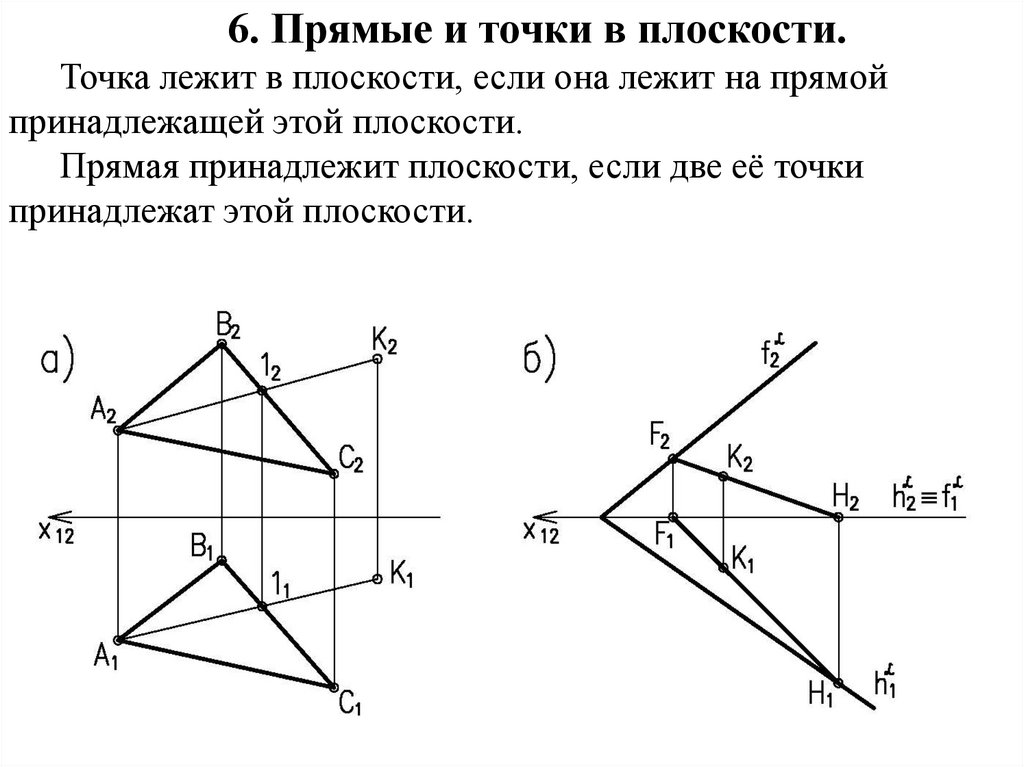
6. Прямые и точки в плоскости.
Точка лежит в плоскости, если она лежит на прямой
принадлежащей этой плоскости.
Прямая принадлежит плоскости, если две её точки
принадлежат этой плоскости.

18.

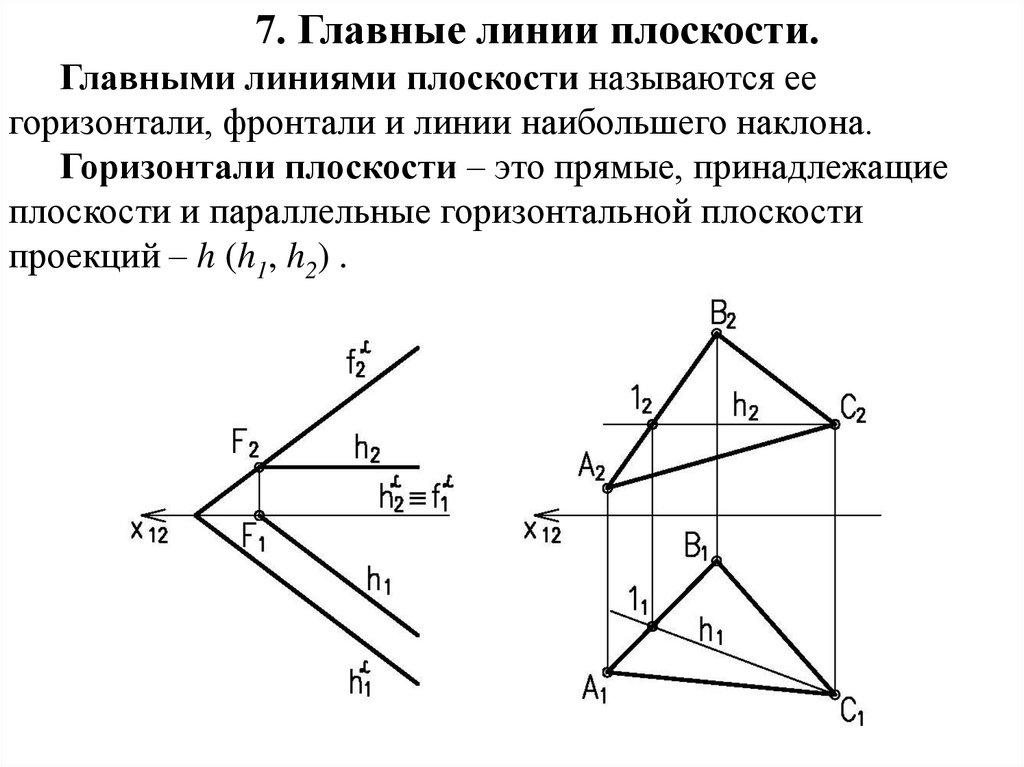
7. Главные линии плоскости.
Главными линиями плоскости называются ее
горизонтали, фронтали и линии наибольшего наклона.
Горизонтали плоскости – это прямые, принадлежащие
плоскости и параллельные горизонтальной плоскости
проекций – h (h1, h2) .

19.

Фронтали плоскости – это прямые, принадлежащие
плоскости и параллельны фронтальной плоскости проекций –
f (f1, f2).

20.

8. Плоскости частного положения.
Плоскости, перпендикулярные или параллельные одной из
плоскостей проекций – плоскости частного положения.
Плоскости, перпендикулярные одной из плоскостей
проекций, называются проецирующими.
а) – горизонтально проецирующая плоскость
б) – фронтально проецирующая плоскость

21.

Плоскости, параллельные одной из плоскостей проекций,
называются плоскостями уровня.
а) – горизонтальная плоскость уровня β, заданная
треугольником АВС,
б) – фронтальная плоскость уровня ε заданная
пересекающимися прямыми mn.

22.

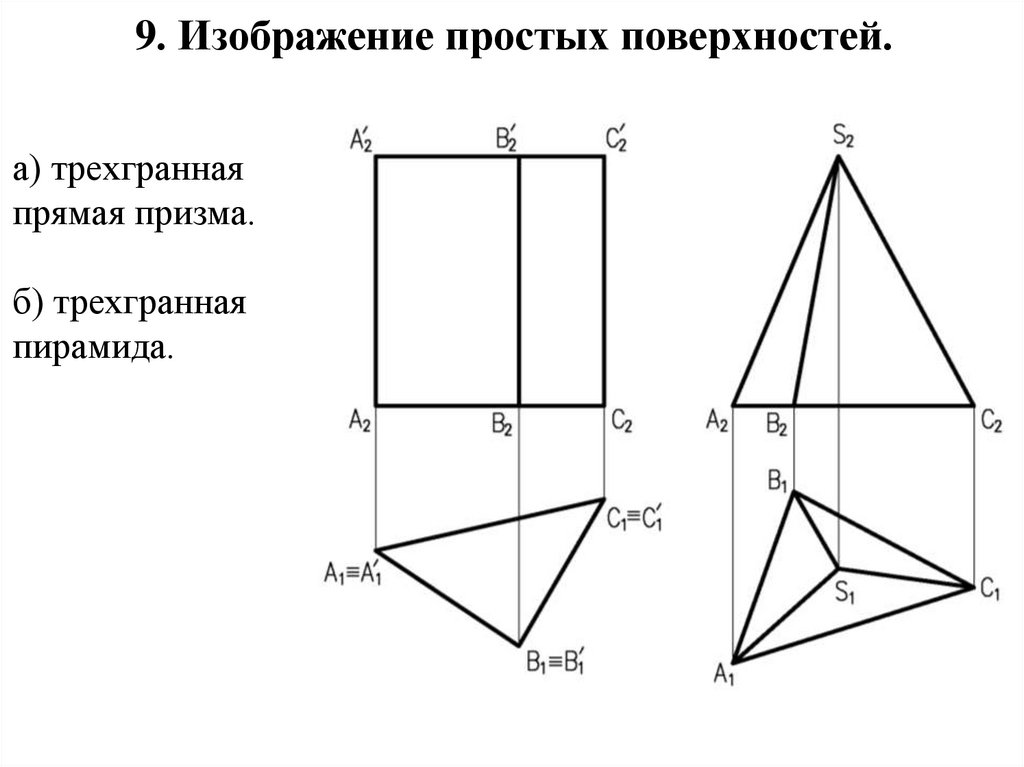
9. Изображение простых поверхностей.
а) трехгранная
прямая призма.
б) трехгранная
пирамида.

23.

а) – прямой цилиндр.
б) – прямой конус.