Основные задачи начертательной геометрии

1.

Основные задачи начертательной
геометрии:
• изучение и разработка методов проецирования
(моделирования) геометрических объектов на
плоскость;
• исследование геометрических преобразований
и их свойств;
• разработка методов решения пространственных
геометрических задач на плоских
изображениях;
• разработка
условий,
обеспечивающих
обратимость
чертежа
и
качественное
изготовление изделия с учетом новых
технологий.

2.

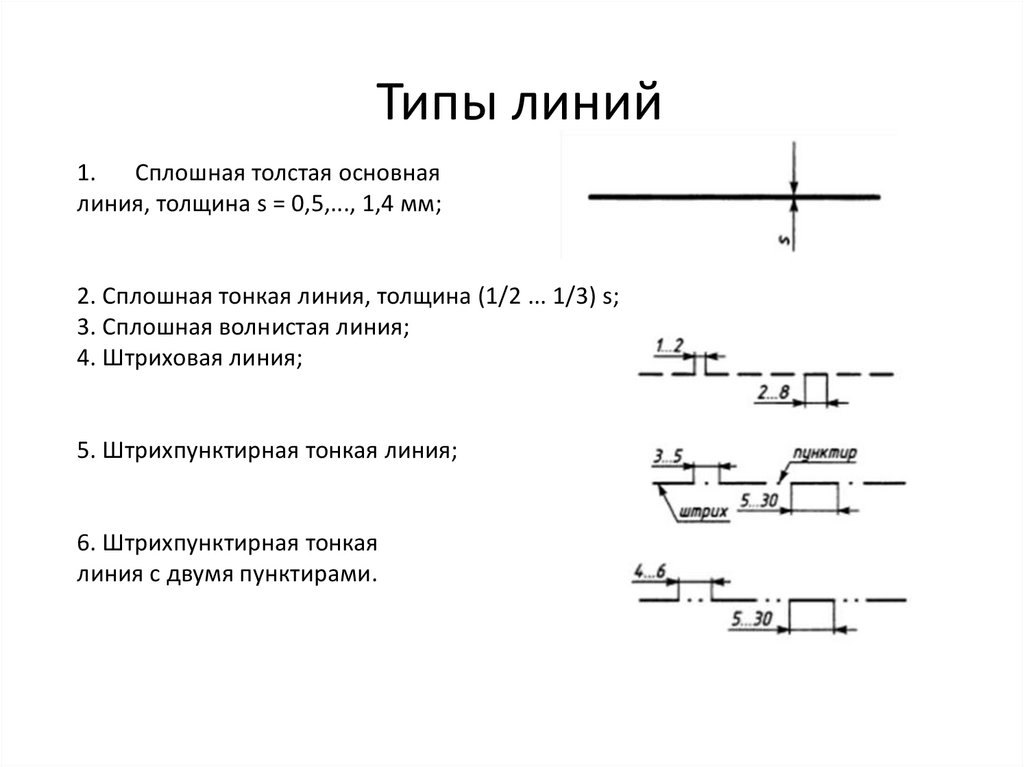
Типы линий
1. Сплошная толстая основная
линия, толщина s = 0,5,..., 1,4 мм;
2. Сплошная тонкая линия, толщина (1/2 ... 1/3) s;
3. Сплошная волнистая линия;
4. Штриховая линия;
5. Штрихпунктирная тонкая линия;
6. Штрихпунктирная тонкая
линия с двумя пунктирами.

3.

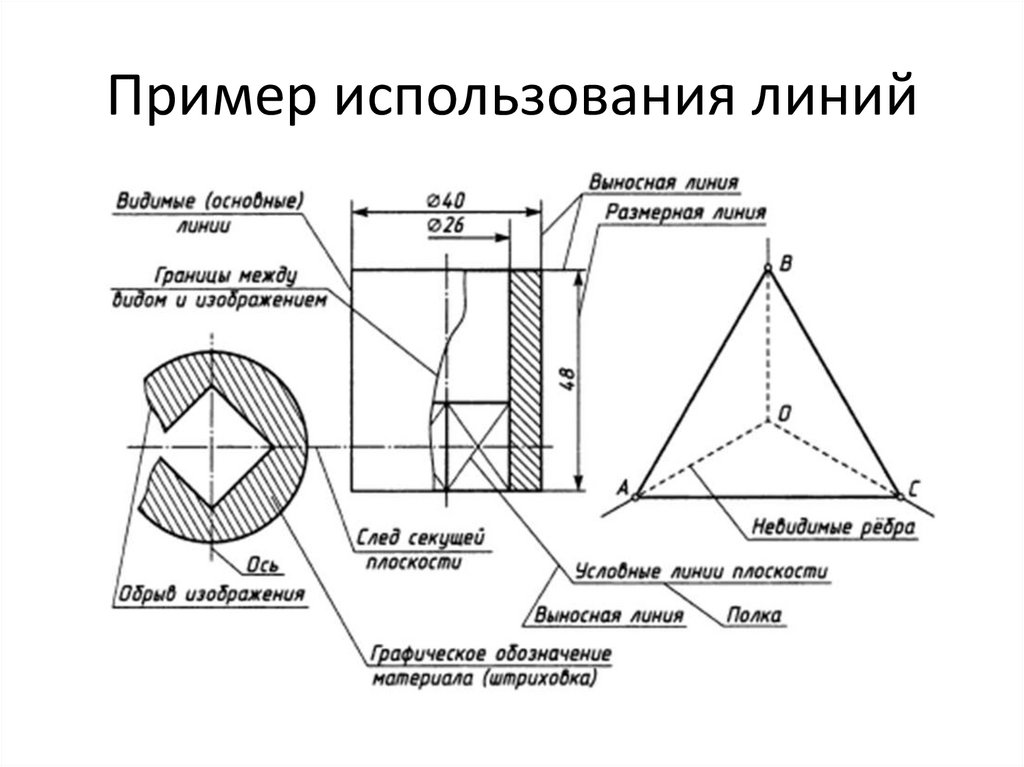
Пример использования линий

4.

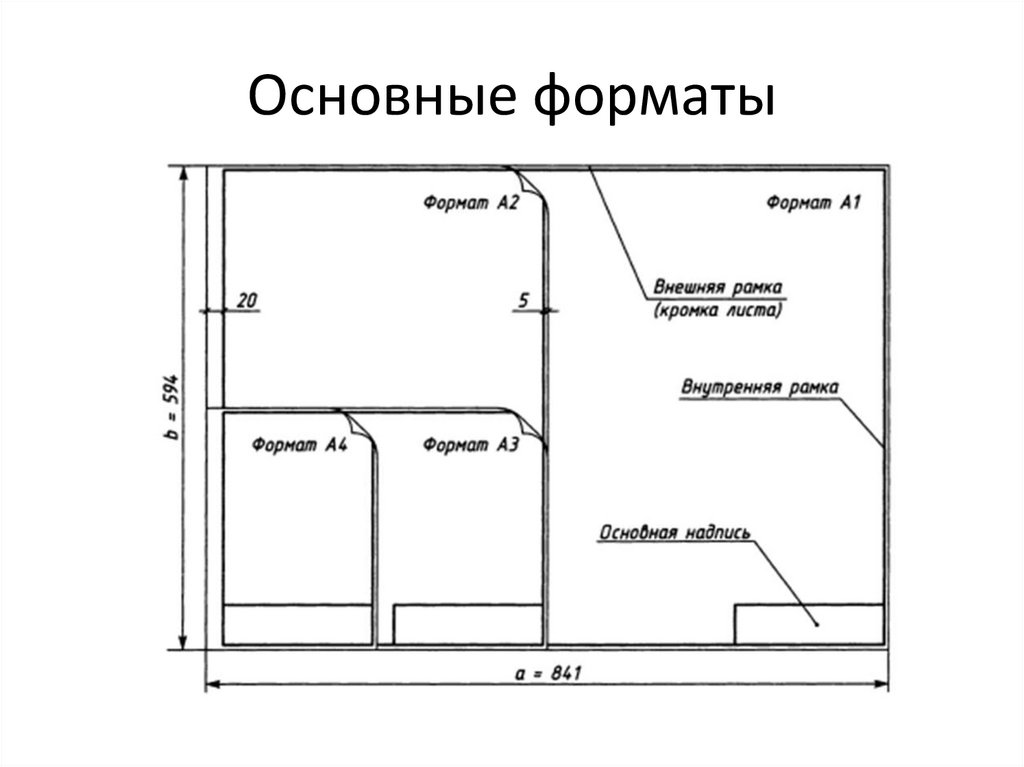
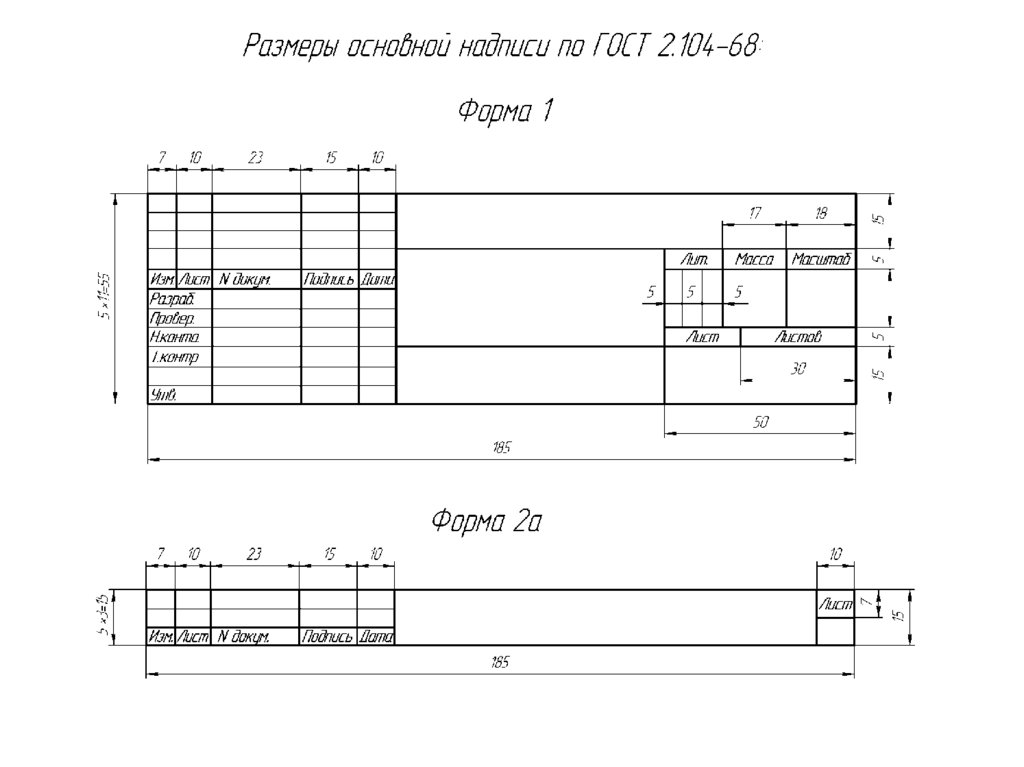
Основные форматы

5.

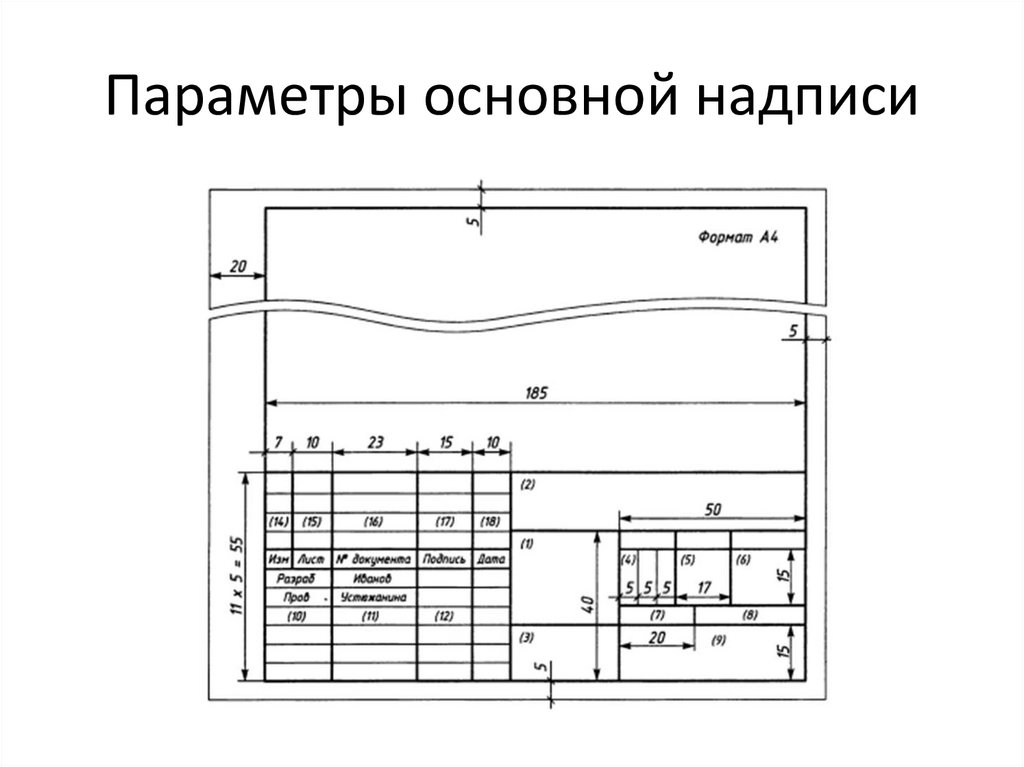
Параметры основной надписи

6.

7.

8.

Масштабы
Масштаб обозначают буквой ≪М≫ и
записывают отношением.
ГОСТ 2.302-68 Масштабы для изображения на
чертежах устанавливает:
• масштабы уменьшения:
1:2; 1:2,5; 1:4; 1:5; 1:10;
• натуральная величина: 1:1;
• масштабы увеличения:
2:1; 2,5:1; 4:1; 5:1; 10:1

9.

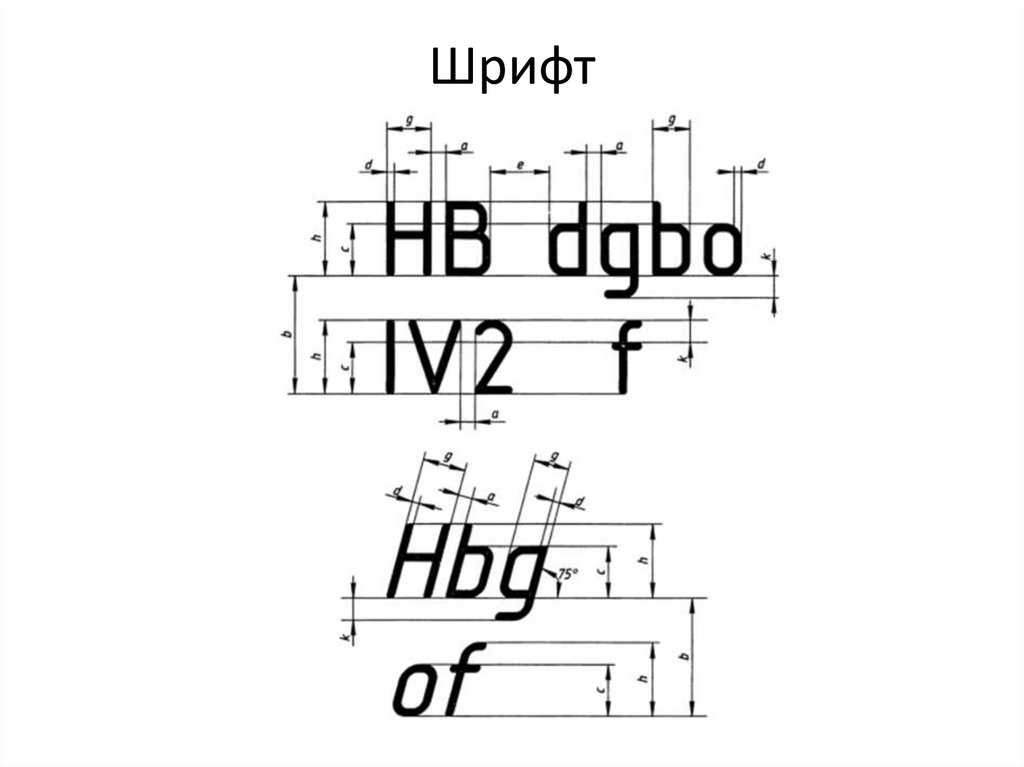
Шрифт

10.

11.

12.

Ерунда — штука гордая, в чью попало голову добровольно не
придет.
Идеальный дом — это сумма всех комнат, где тебе хорошо
жилось.
Старшая сестра — это такое специальное божье наказание. Она
всегда оказывается права.
Запомни раз и навсегда: всякое существо рождается для того,
чтобы познавать мир. А не для того, чтобы всем в этом мире
понравиться.
Ждать и надеяться - верный способ скоропостижно рехнуться, а
вот носиться по городу и делать глупости - это именно то, что
надо!
"Завтра" - одно из самых опасных слов на свете. Парализует
волю похлеще иного заклинания, склоняет к бездействию, в
зародыше уничтожает планы и идеи.
Цикл книг о Максе Фрае

13.

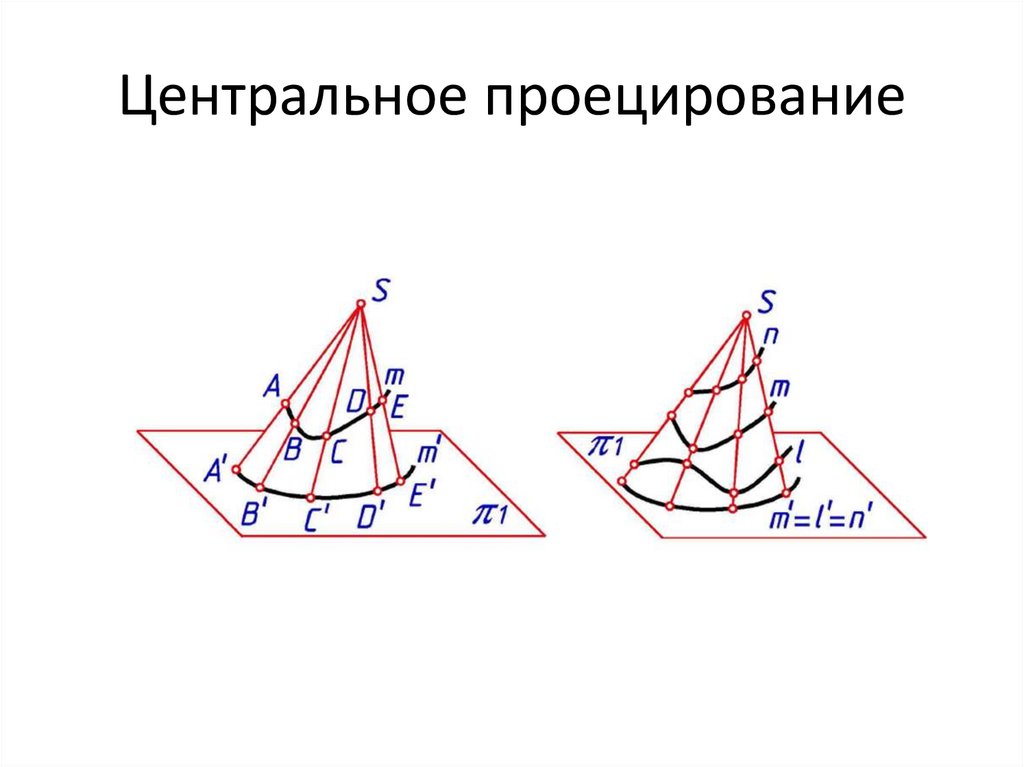
Центральное проецирование

14.

Параллельное проецирование

15.

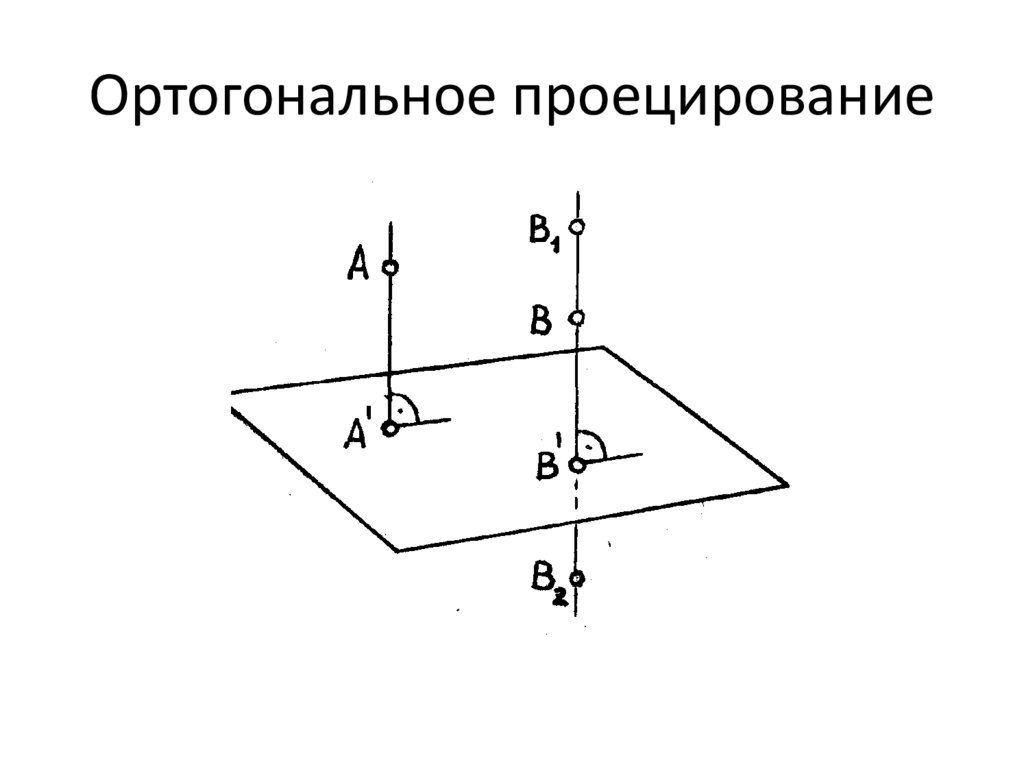
Ортогональное проецирование

16.

Свойства ортогонального
проецирования
1.
Проекция точки на плоскость есть точка.
2.
Проекция прямой на плоскость в общем
случае есть прямая. Она вырождается в
точку, если прямая параллельна
направлению проецирования.
3.
Если точка принадлежит линии, то
проекция точки принадлежит проекции
этой линии.

17.

4. Если отрезок прямой линии делится точкой в
каком-либо отношении, то и проекция отрезка
делится проекцией точки в том же отношении.
5. Точка пересечения линий проецируется в точку
пересечения их проекций.
6. Проекции отрезков параллельных прямых
параллельны, и их длины находятся в таком же
отношении, как и длины проецируемых отрезков.
7. Проекции двух скрещивающихся прямых линий в
зависимости от направления проецирования могут
пересекаться или быть параллельными.

18.

8. При прямоугольном проецировании прямой угол
проецируется без искажения (прямым углом), если
одна из его сторон параллельна плоскости
проекций, а другая не перпендикулярна ей.
9. Плоская фигура, параллельная плоскости
проекций, проецируется на эту плоскость без
искажения.
10. При параллельном перемещении фигуры или
плоскости проекций изображение фигуры на этой
плоскости не изменяется.

19.

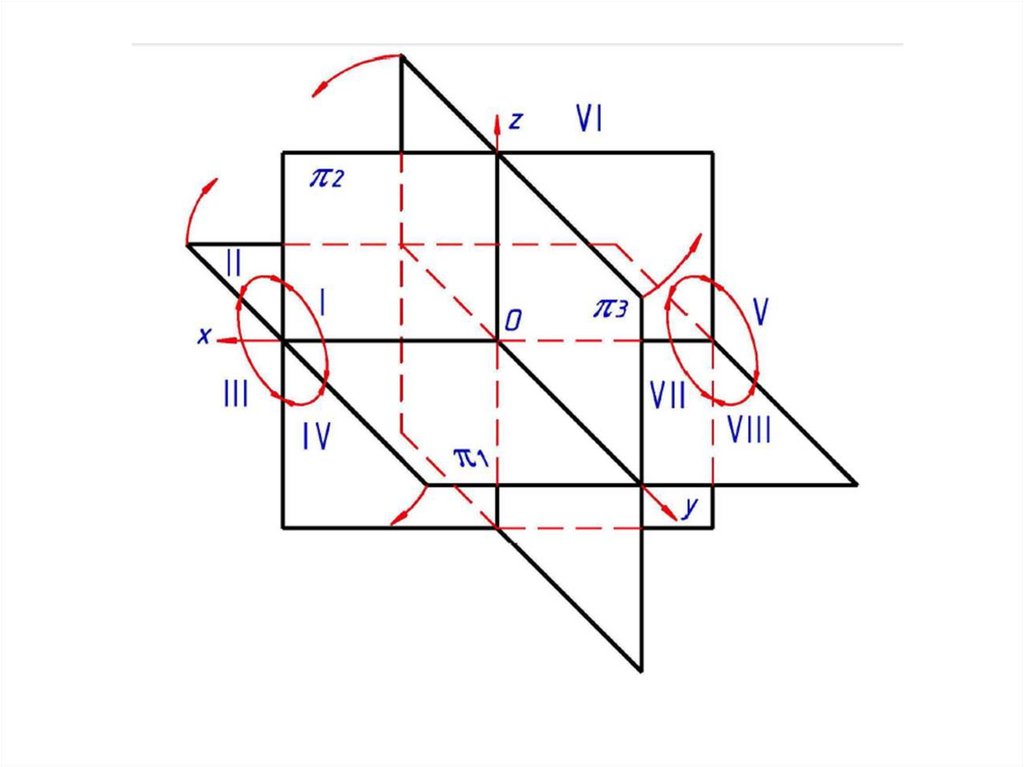
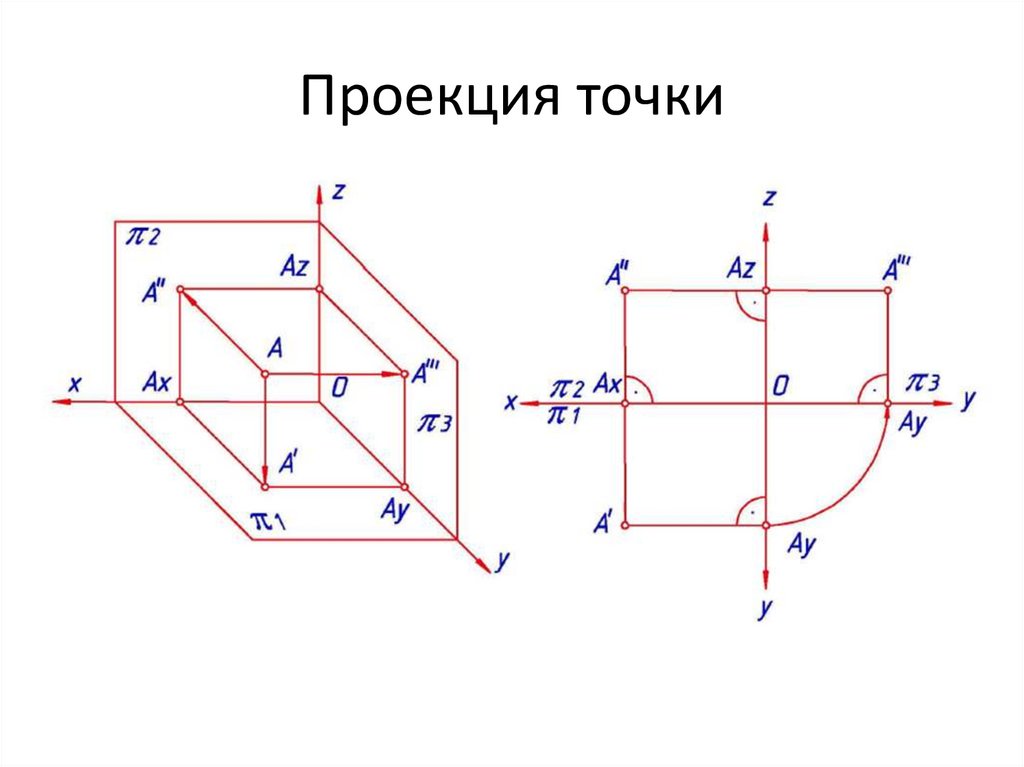
Комплексный чертеж.
П1 - горизонтальная плоскость проекций;
П2 - фронтальная плоскость проекций;
П3 - профильная плоскость проекций.
Комплексный чертеж (эпюр)- плоский чертеж,
составленный из двух или трех связанных между
собой ортогональных проекции геометрической
фигуры.

20.

21.

Проекция точки

22.

23.

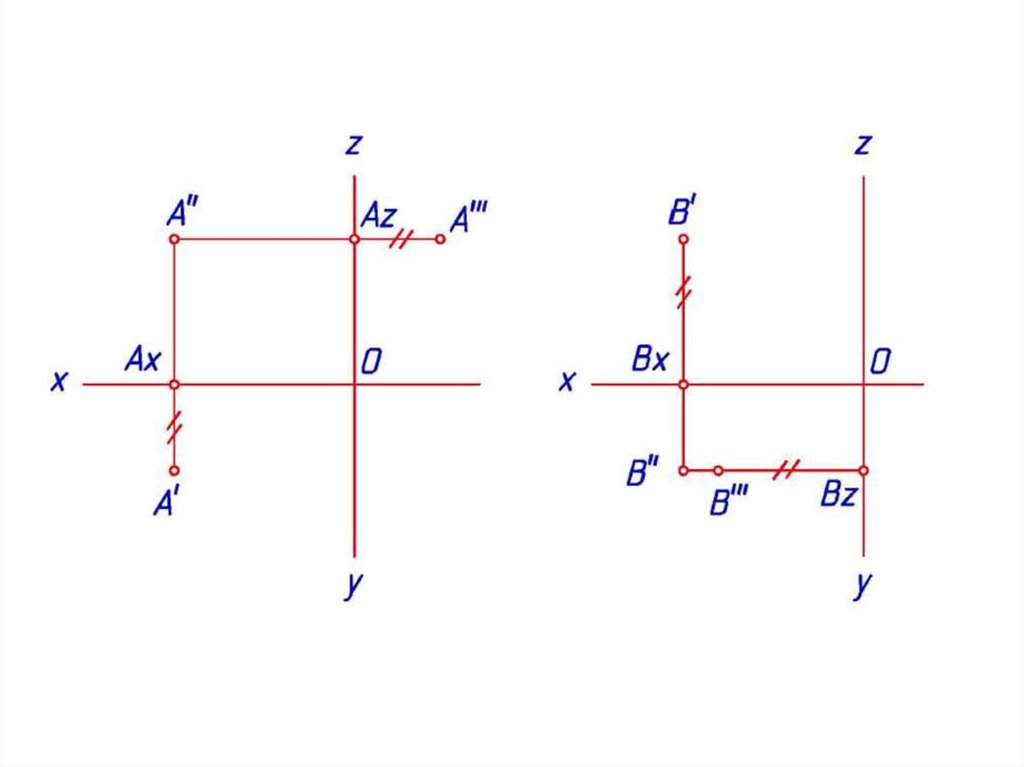
Проекции прямой линии

24.

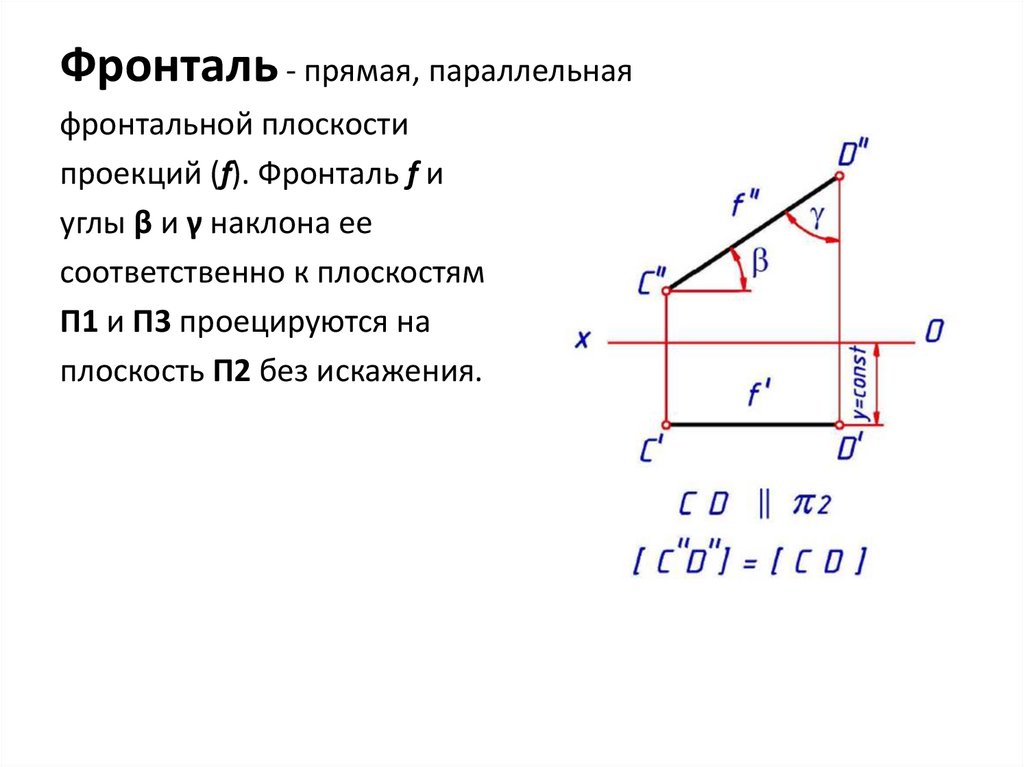
Прямые уровня

25.

Фронталь - прямая, параллельная
фронтальной плоскости
проекций (f). Фронталь f и
углы β и γ наклона ее
соответственно к плоскостям
П1 и П3 проецируются на
плоскость П2 без искажения.

26.

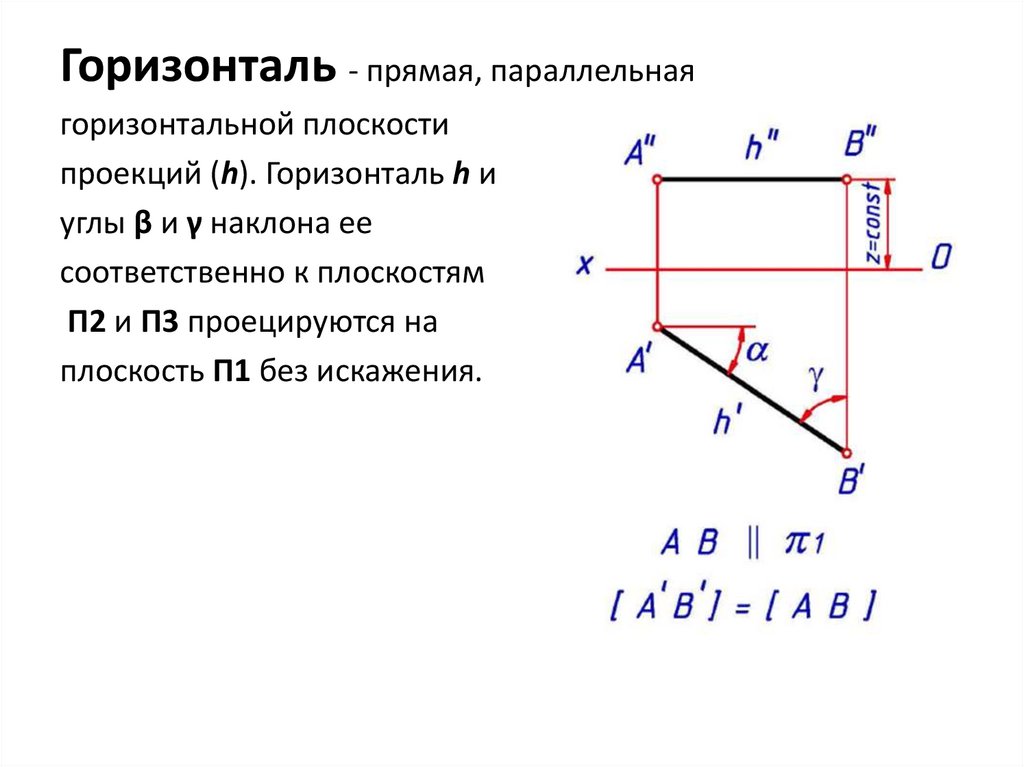
Горизонталь - прямая, параллельная
горизонтальной плоскости
проекций (h). Горизонталь h и
углы β и γ наклона ее
соответственно к плоскостям
П2 и П3 проецируются на
плоскость П1 без искажения.

27.

Профильная прямая - прямая, параллельная
профильной плоскости проекций. Профильная прямая
обозначается буквой р. Фронтальная и горизонтальная
проекции профильной прямой располагаются параллельна
оси Z, или, что то же, перпендикулярно к оси Х.

28.

Проецирующие
прямые

29.

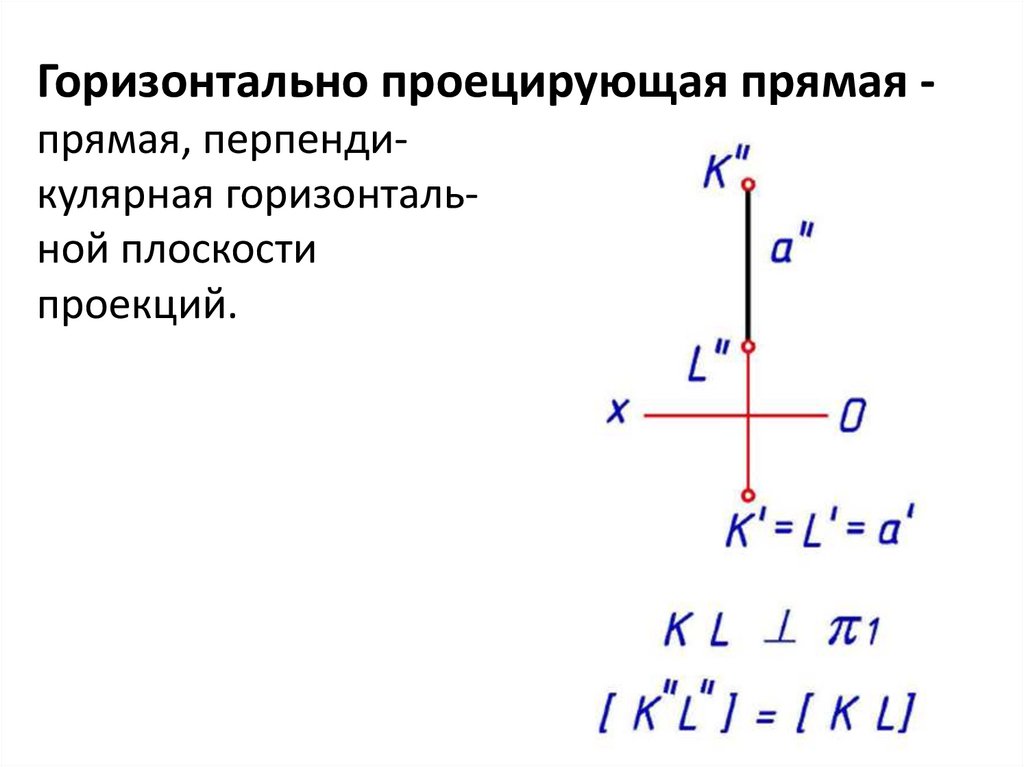
Горизонтально проецирующая прямая прямая, перпендикулярная горизонтальной плоскости
проекций.

30.

Фронтально проецирующая прямая прямая, перпендикулярная фронтальной плоскости
проекций. Фронтальная проекция
прямой вырождается в точку,
а на плоскости П1 и П3 она
проецируется без искажения.

31.

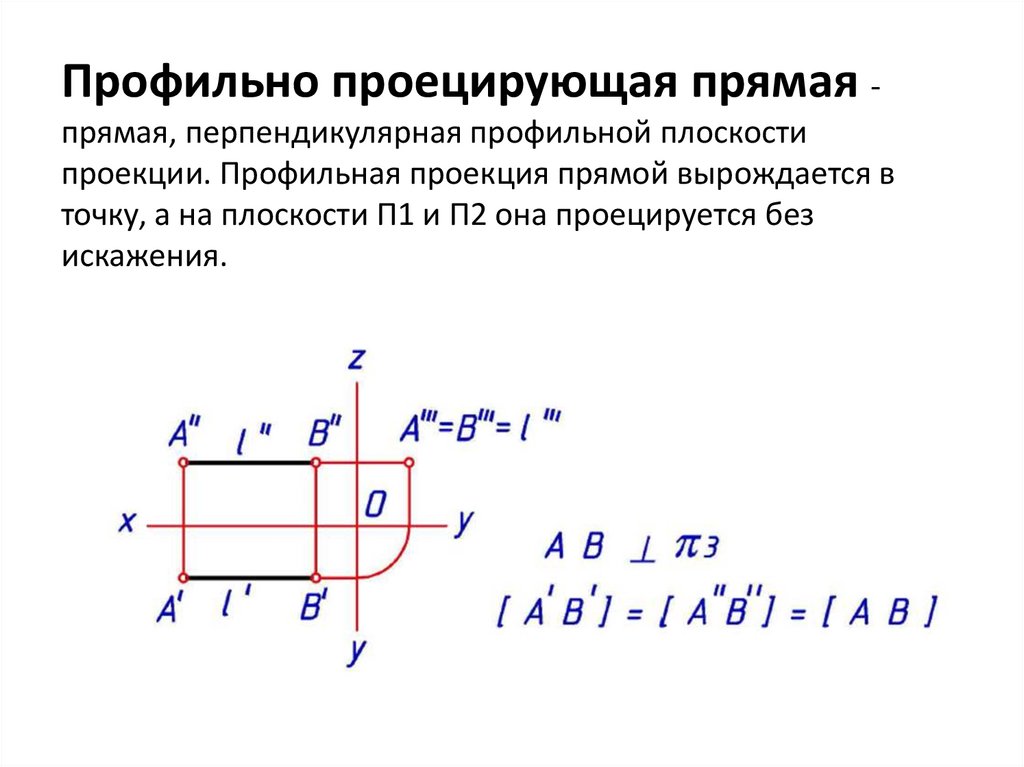
Профильно проецирующая прямая прямая, перпендикулярная профильной плоскости
проекции. Профильная проекция прямой вырождается в
точку, а на плоскости П1 и П2 она проецируется без
искажения.

32.

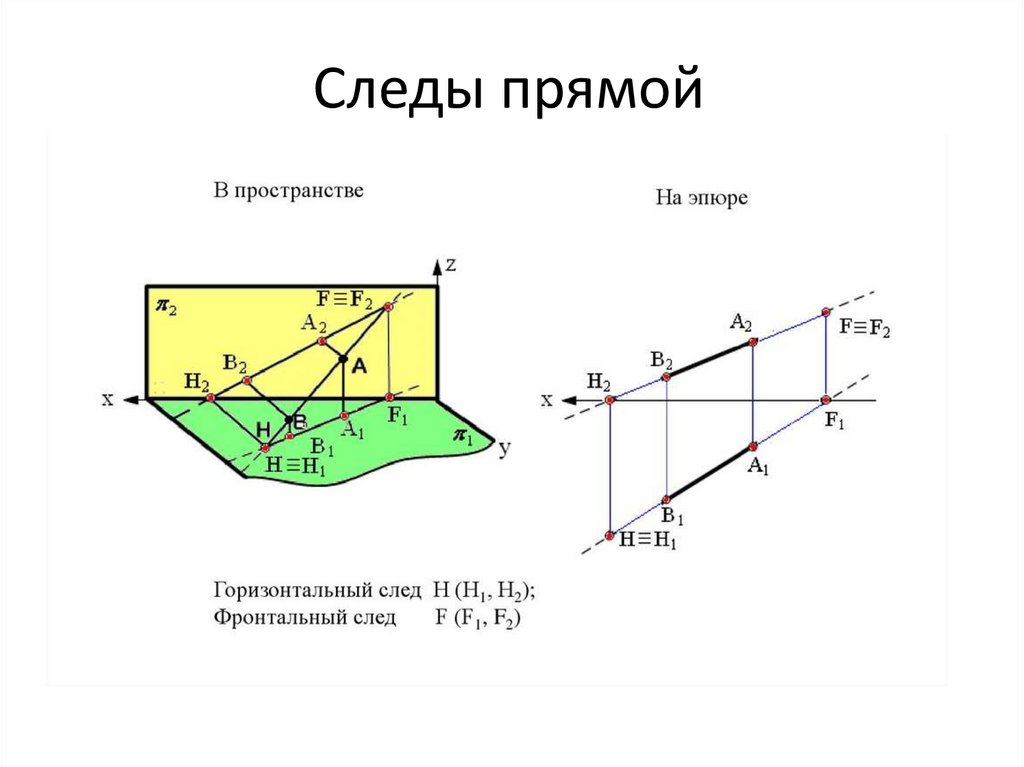
Следы прямой

33.

Определение натуральной
величины отрезка прямой способом
прямоугольного треугольника.

34.

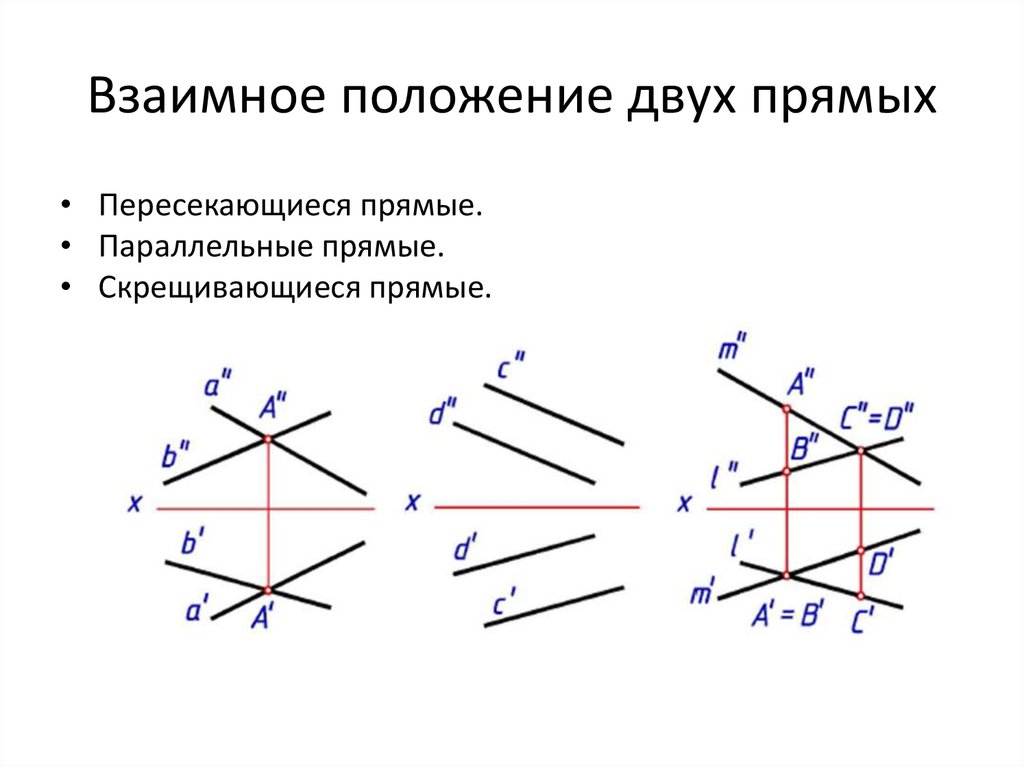
Взаимное положение двух прямых
• Пересекающиеся прямые.
• Параллельные прямые.
• Скрещивающиеся прямые.

35.

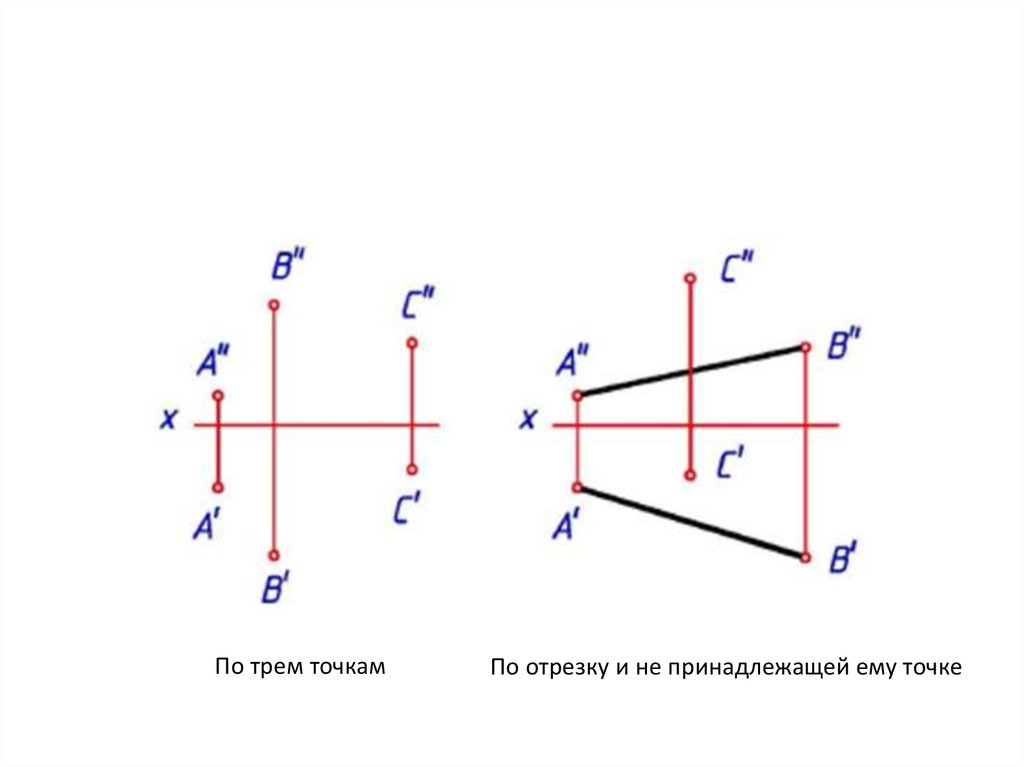
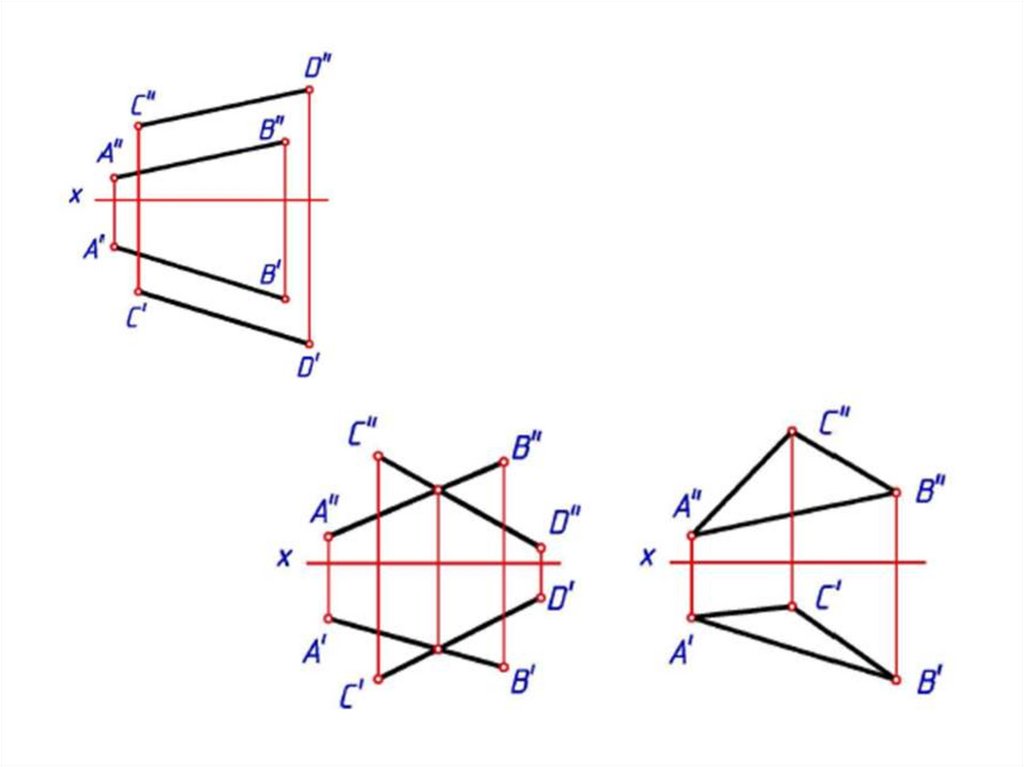
Способы задания плоскости на
комплексном чертеже.
• Проекциями трех точек, не лежащих на одной
прямой.
• Проекциями прямой и не принадлежащей ей
точки.
• Проекциями двух параллельных прямых.
• Проекциями двух пересекающихся прямых.
• Проекциями плоской фигуры, например
треугольника.
• Следами плоскости.

36.

По трем точкам
По отрезку и не принадлежащей ему точке

37.

38.

39.

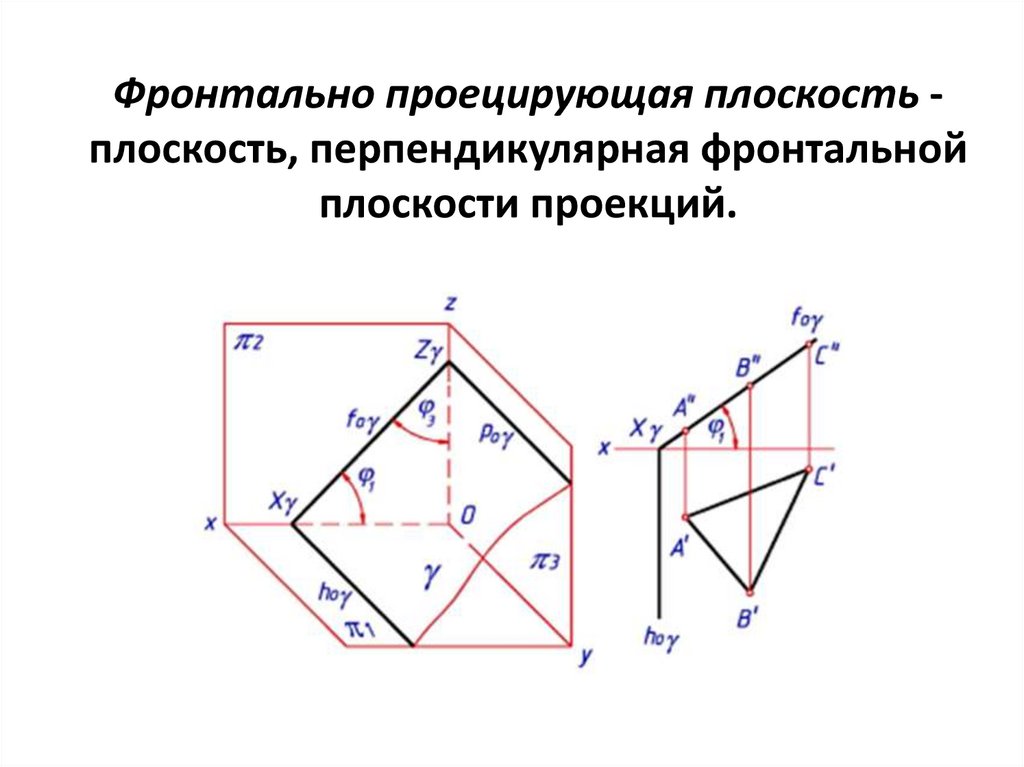
Проецирующие плоскости

40.

Фронтально проецирующая плоскость плоскость, перпендикулярная фронтальной
плоскости проекций.

41.

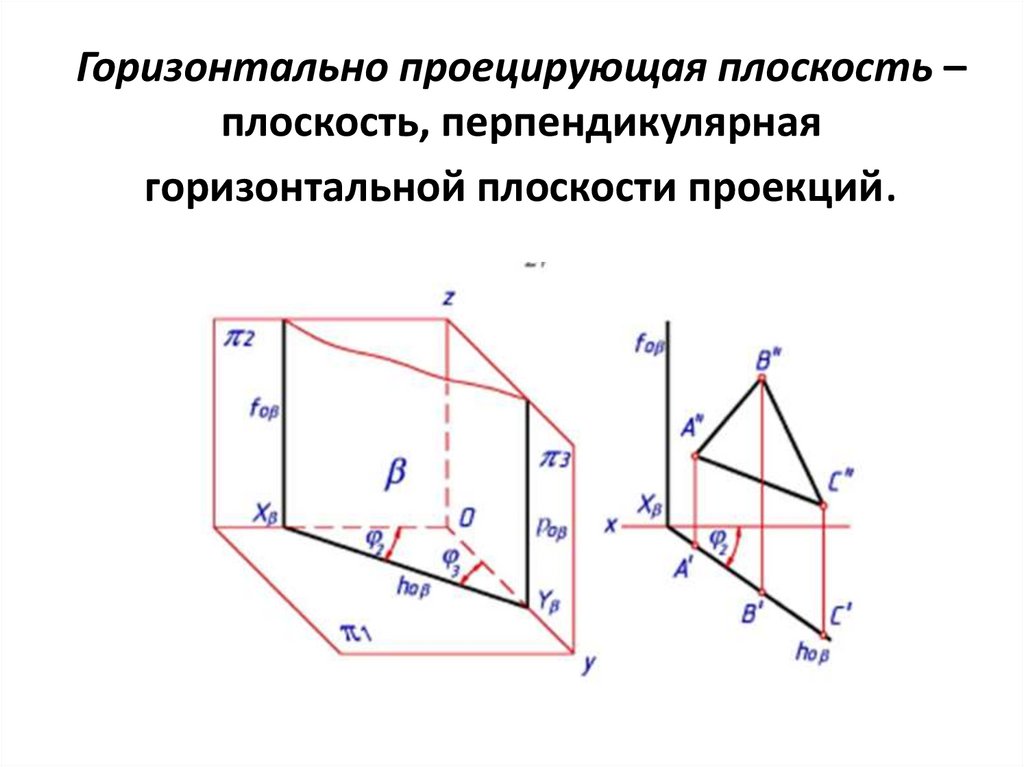
Горизонтально проецирующая плоскость –
плоскость, перпендикулярная
горизонтальной плоскости проекций.

42.

Профильно проецирующая плоскость плоскость, перпендикулярная профильной
плоскости проекций.

43.

Плоскости уровня.

44.

Горизонтальная плоскость - плоскость,
параллельная горизонтальной плоскости
проекций.

45.

• Фронтальная плоскость - плоскость,
параллельная фронтальной плоскости
проекций.
• Профильная плоскость - плоскость,
параллельная профильной плоскости
проекций.
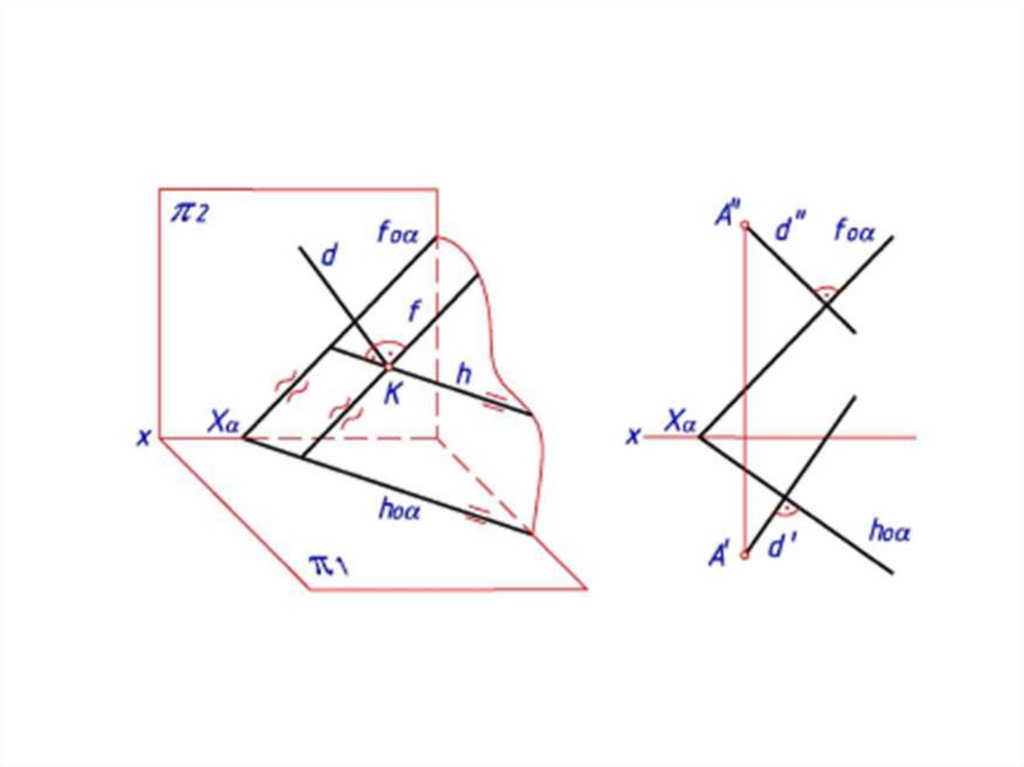
Точка принадлежит плоскости, если ее проекции
принадлежат одноименным проекциям прямой
этой плоскости. В плоскости через точку можно
провести множество прямых.

46.

Взаимное положение плоскостей
• Плоскости параллельны, если две
пересекающиеся прямые одной плоскости
соответственно параллельны двум
пересекающимся прямым другой
плоскости.
• Прямая перпендикулярна плоскости, если
она перпендикулярна двум
пересекающимся прямым этой плоскости.