Начертательная геометрия. Лекция 1

1. Начертательная геометрия

2. Литература

• В.О. Гордон, М.А. Семенцов-Огиевский «Курс
начертательной геометрии»;
• С.А. Фролов «Начертательная геометрия»;
• Стандарты ЕСКД;

3.

• О.В. Бразговка, О.П. Микова «Начертательная
геометрия» рабочая тетрадь №1 с печатной
основой для записи конспекта лекций;
• О.В. Бразговка, О.П. Микова, Н.В. Кнапнугель
«Начертательная геометрия» рабочая тетрадь №2;
• О.В. Бразговка, Н.В. Кнапнугель, С.И. Нюкалова
«Инженерная графика» рабочая тетрадь №5.

4.

• О.В. Бразговка, Н.В. Кнапнугель, Г.А.
Мальцева «Начертательная геометрия»
эпюры 1, 2, 3

5. Условные обозначения

1. Точки в пространстве – прописными буквами латинского алфавита : A, B,
C,… а также цифрами: 1, 2, 3, …
2. Линии в пространстве, произвольно расположенные по отношению к плоскостям проекции, – строчными буквами латинского алфавита: a, b, l, …
3. Плоскости в пространстве – строчными буквами греческого алфавита: α, β, γ
4. Линии уровня:
h – горизонталь;
f – фронталь;
р – профильная прямая уровня.
5. Плоскости проекций:
H – горизонтальная плоскость проекции;
V – фронтальная плоскость проекции;
W – профильная плоскость проекции.
6. Углы наклона прямой или плоскости к плоскостям проекции:
α – к плоскости Н;
β – к плоскости V;
γ – к плоскости W.

6.

7. Углы – строчными буквами греческого алфавита: θ, φ, ω, …
8. Проекции точек:
на горизонтальную плоскость проекции Н – А', В', С', …;
на фронтальную плоскость проекции V – А'', В'', С'', …;
на профильную плоскость проекции W – А''', В''', С''', ….
9. Проекции линий:
на горизонтальную плоскость проекции Н – a', b', c', …;
на фронтальную плоскость проекции V – a'', b'', c'', …;
на профильную плоскость проекции W – a''', b''', c''', ….
10. Оси проекций:
x – ось абсцисс;
y – ось ординат;
z – ось аппликат.
11. Сокращенные обозначения произвольных операций:
знак параллельности – ∥;
знак совпадения (тождества) – ≡;
знак перпендикулярности – ⊥;
знак принадлежности - ∈.

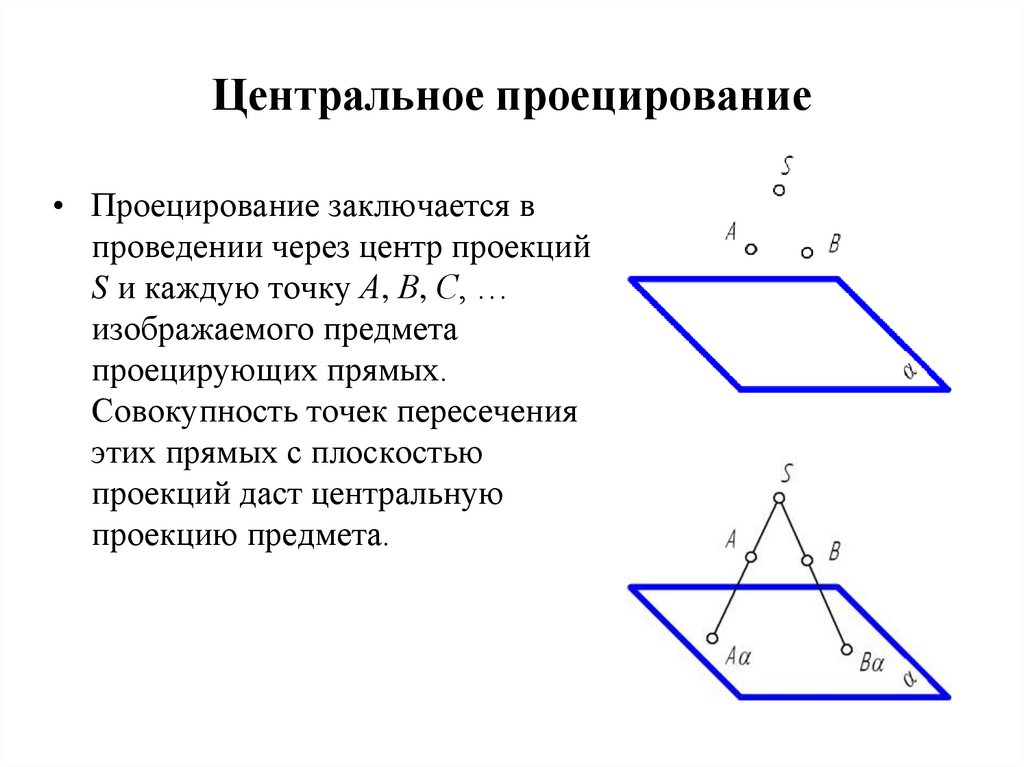
7. Центральное проецирование

• Проецирование заключается в
проведении через центр проекций
S и каждую точку А, В, С, …
изображаемого предмета
проецирующих прямых.
Совокупность точек пересечения
этих прямых с плоскостью
проекций даст центральную
проекцию предмета.

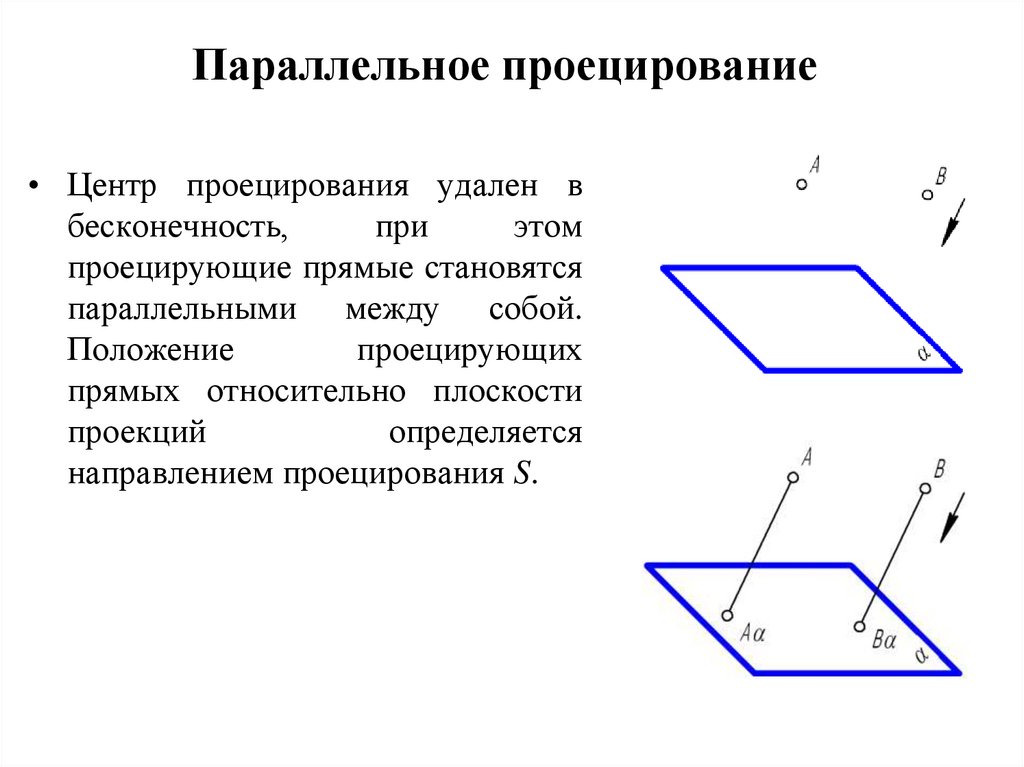
8. Параллельное проецирование

• Центр проецирования удален в
бесконечность,
при
этом
проецирующие прямые становятся
параллельными между собой.
Положение
проецирующих
прямых относительно плоскости
проекций
определяется
направлением проецирования S.

9. Основные инвариантные свойства параллельного проецирования

• Геометрические фигуры проецируются на
плоскость проекции, в общем случае, с
искажением.
• При этом характер искажений проекций по
сравнению с оригиналом зависит от аппарата
проецирования и положения проецируемой
фигуры по отношению к плоскости проекций.

10.

• Наряду с этим, между оригиналом и его
проекцией существует определенная связь,
заключающаяся в том, что некоторые
свойства оригинала сохраняются и на его
проекции. Такие свойства принято называть
инвариантными (независимыми) для
данного способа проецирования.
• Отметим основные инвариантные свойства
параллельного проецирования:

11.

1. проекция точки есть точка;
2. проекция прямой на плоскость есть прямая;
3. если в пространстве точка принадлежит
прямой, то проекция точки принадлежит
проекции этой прямой;

12.

4. проекции взаимно параллельных прямых также
взаимно параллельны, а отношение отрезков таких
прямых равно отношению их параллельных
проекций;
а) если отрезок прямой делится точкой в какомлибо отношении, то и проекция отрезка делится
проекцией этой точки в том же отношении;
б) проекции конгруэнтных отрезков взаимно
параллельных прямых взаимно параллельны и
конгруэнтны
(поэтому
проекцией
любого
параллелограмма будет параллелограмм);

13.

5. точка пересечения проекций
пересекающихся прямых является проекцией
точки пересечения этих прямых;
6. плоская фигура, параллельная плоскости
проекции, проецируется на эту плоскость в
конгруэнтную фигуру;
7. плоский многоугольник, в общем случае,
проецируется в многоугольник с тем же
числом вершин.

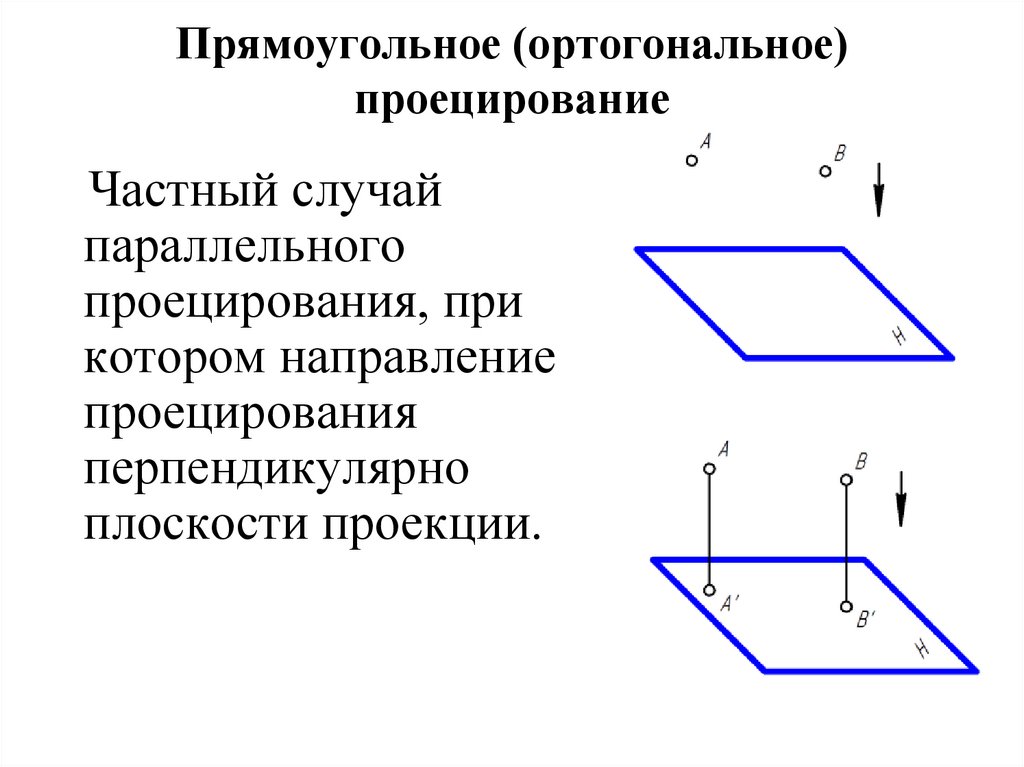
14. Прямоугольное (ортогональное) проецирование

Частный случай
параллельного
проецирования, при
котором направление
проецирования
перпендикулярно
плоскости проекции.

15. Пространственная модель координатных плоскостей проекций

• Сущность метода ортогонального
проецирования заключается в том,
что предмет проецируется на две или
три взаимно перпендикулярные
плоскости проекций проецирующими
прямыми, ортогональными
(перпендикулярными) этим
плоскостям.

16.

• H – горизонтальная плоскость
проекций;
• V – фронтальная плоскость проекций;
• W – профильная плоскость проекций.
• x – ось абсцисс
• y – ось ординат
• z – ось аппликат
• О – начало координат

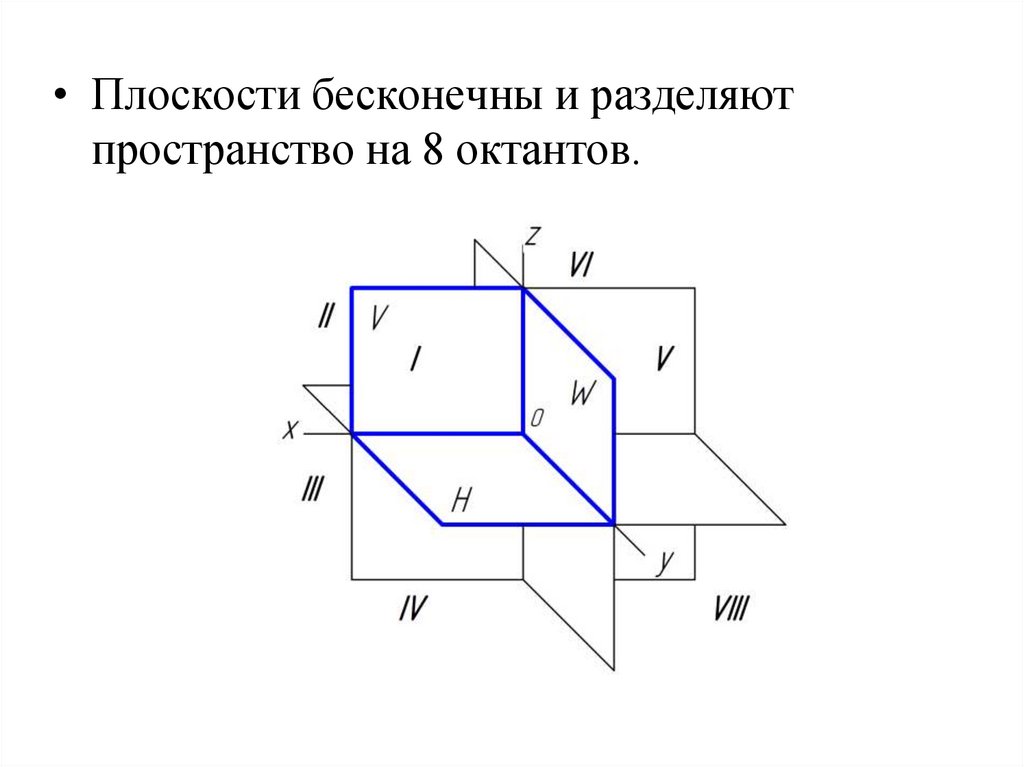
17.

• Плоскости бесконечны и разделяют
пространство на 8 октантов.

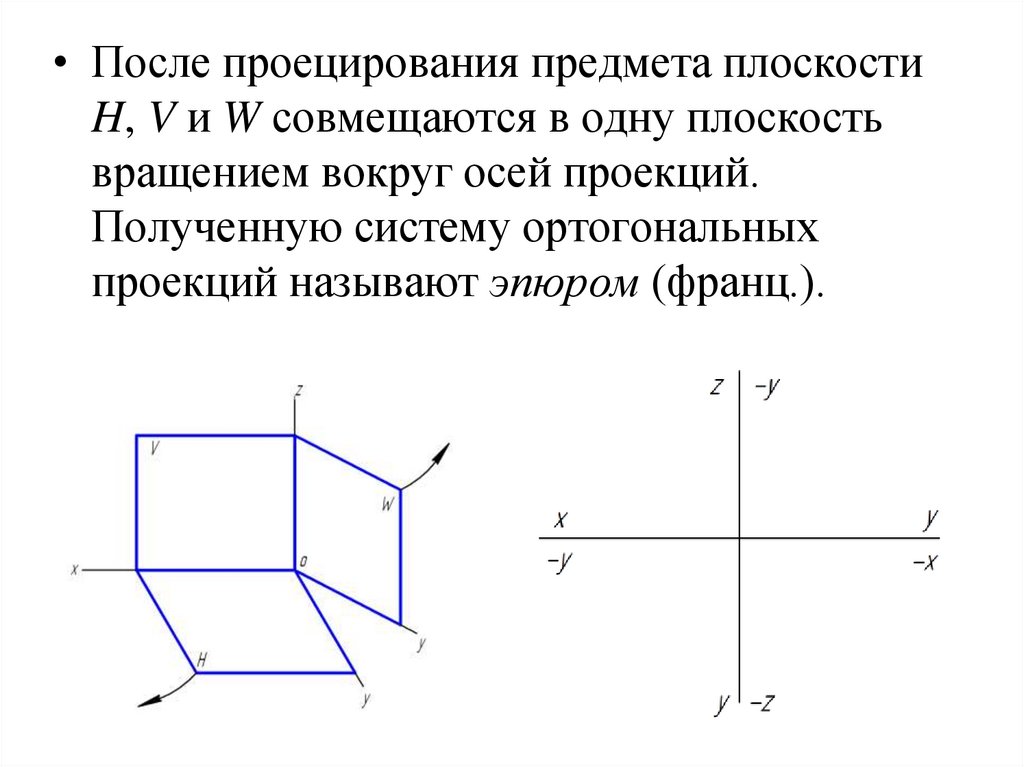
18.

• После проецирования предмета плоскости
H, V и W совмещаются в одну плоскость
вращением вокруг осей проекций.
Полученную систему ортогональных
проекций называют эпюром (франц.).

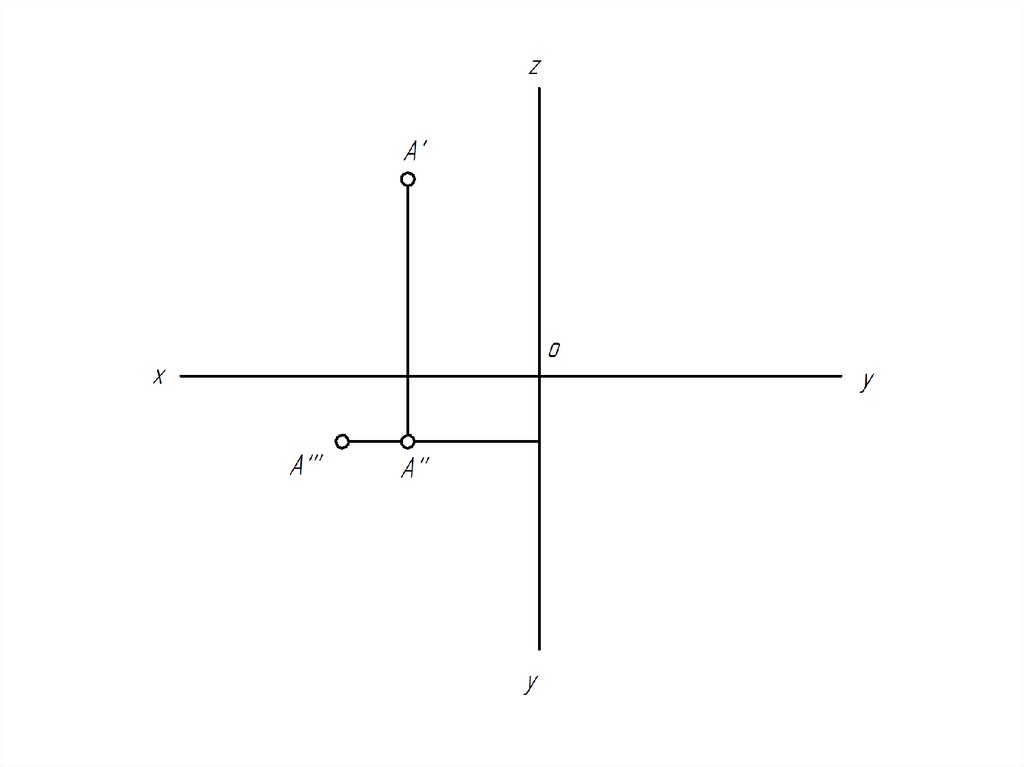
19. 2. Точка в системе трех плоскостей проекции

• В трехмерном пространстве положение
точки определяют с помощью
прямоугольных (декартовых) координат
А(x, y, z).
• Ортогональная проекция точки на плоскости
проекции - основание перпендикуляра,
опущенного из данной точки на эту
плоскость.

20.

• Из точки А проведем перпендикуляры к
плоскостям проекций.
• Определим точки пересечения перпендикуляров с
плоскостями проекций.

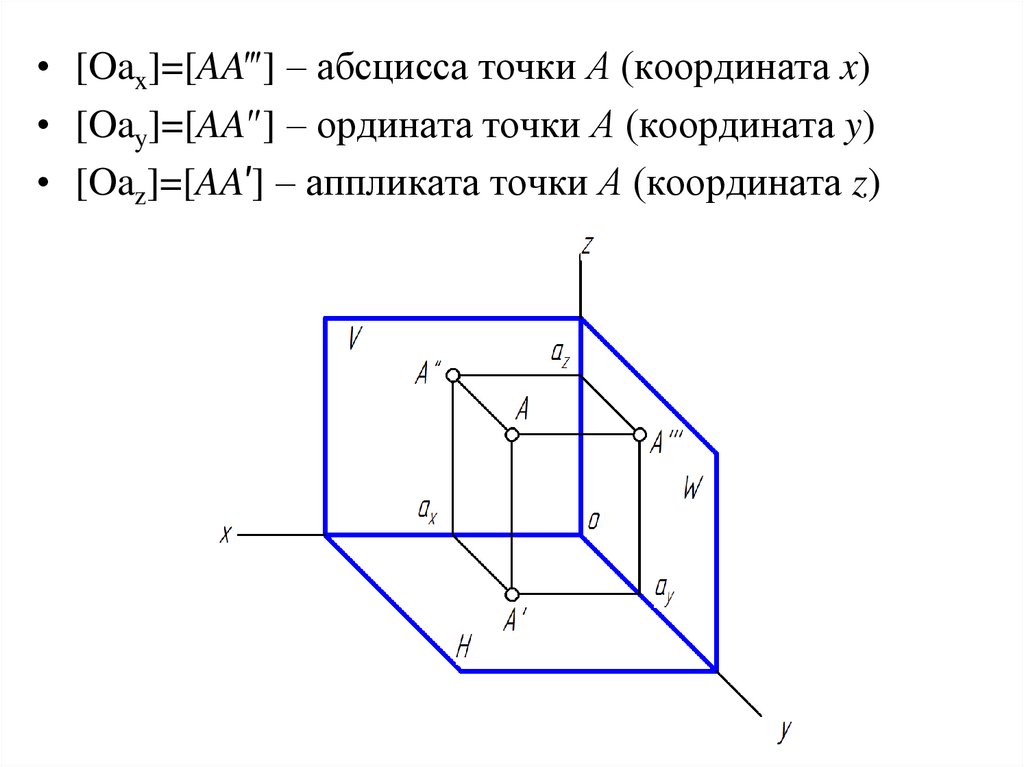
21.

• [Oax]=[AA‴] – абсцисса точки А (координата x)
• [Oay]=[AA″] – ордината точки А (координата y)
• [Oaz]=[AA′] – аппликата точки А (координата z)

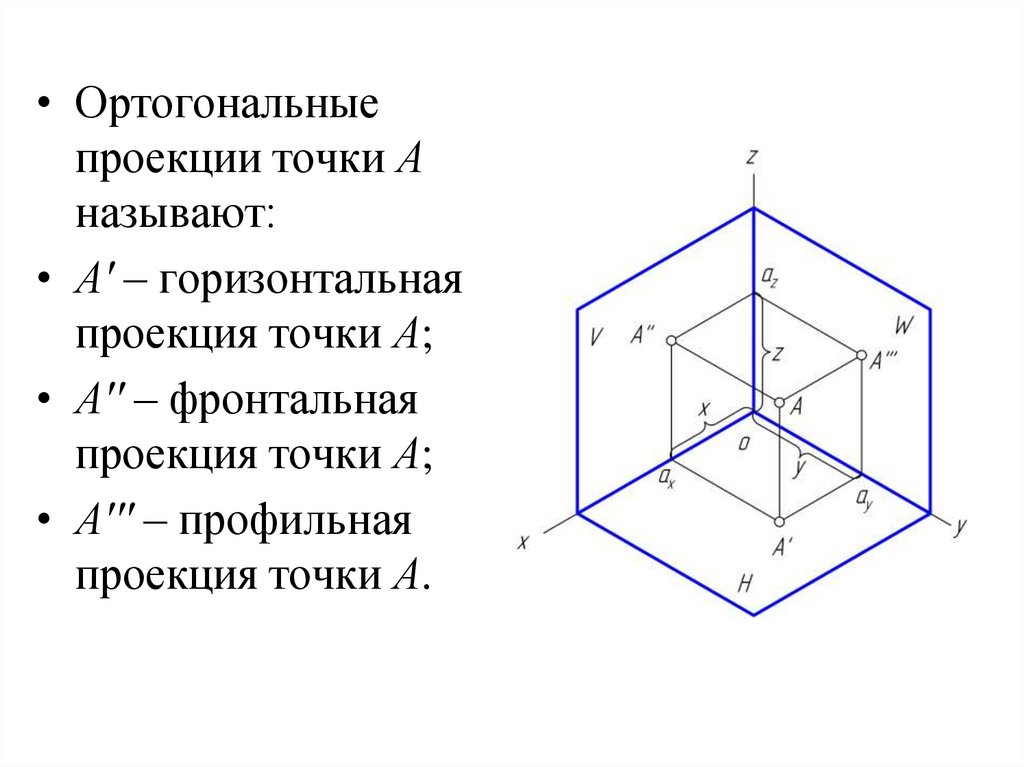
22.

• Ортогональные
проекции точки А
называют:
• А′ – горизонтальная
проекция точки А;
• А′′ – фронтальная
проекция точки А;
• А′′′ – профильная
проекция точки А.

23.

• Положение точки в пространстве вполне
определяется положением ее двух ортогональных
проекций.
• A′ (x, y);
• A″ (x, z);
• A‴ (y, z).
• Как следствие этого – по двум любым заданным
ортогональным проекциям точки всегда можно
построить
недостающую
ее
третью
ортогональную проекцию.
• Прямые линии, соединяющие проекции точки и
перпендикулярные осям проекций, называют
линиями связи

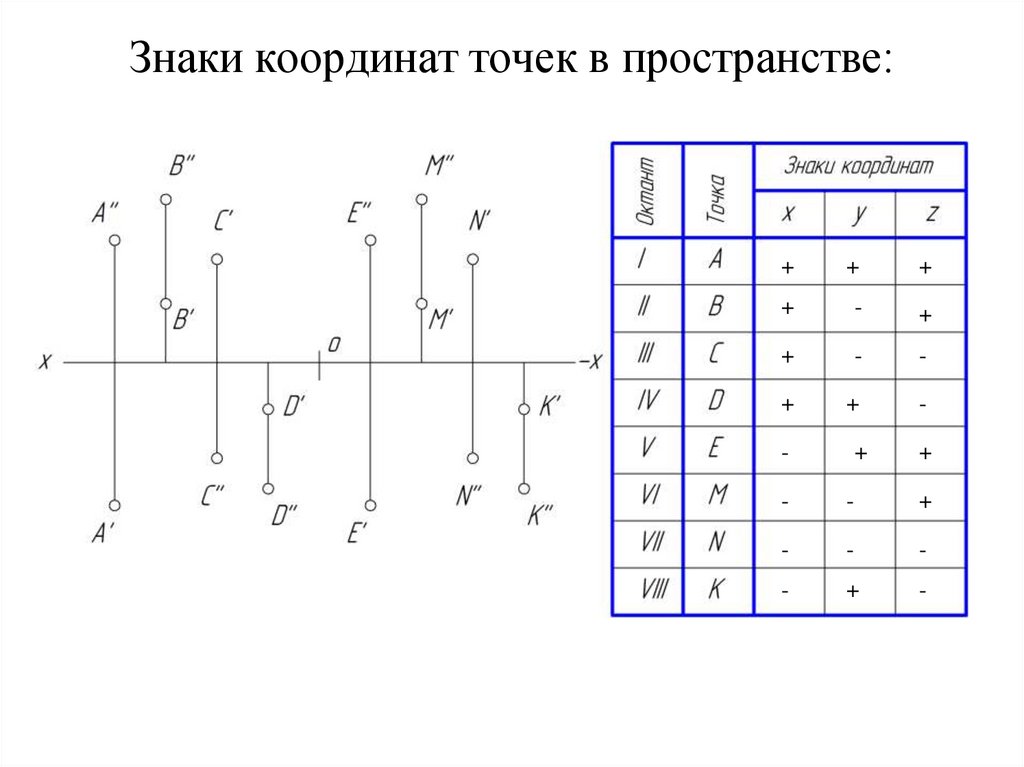
24. Знаки координат точек в пространстве:

+
+
+
+
-
+
+
-
-
+
+
-
-
+
+
-
-
+
-
-
-
-
+
-

25.

Горизонтальная и фронтальная проекции любой
точки принадлежат одной линии связи,
перпендикулярной оси х.
Фронтальная и профильная проекции любой
точки принадлежат одной линии связи,
перпендикулярной оси z.

26.

Построить эпюр точки А(30, 40, 40)

27.

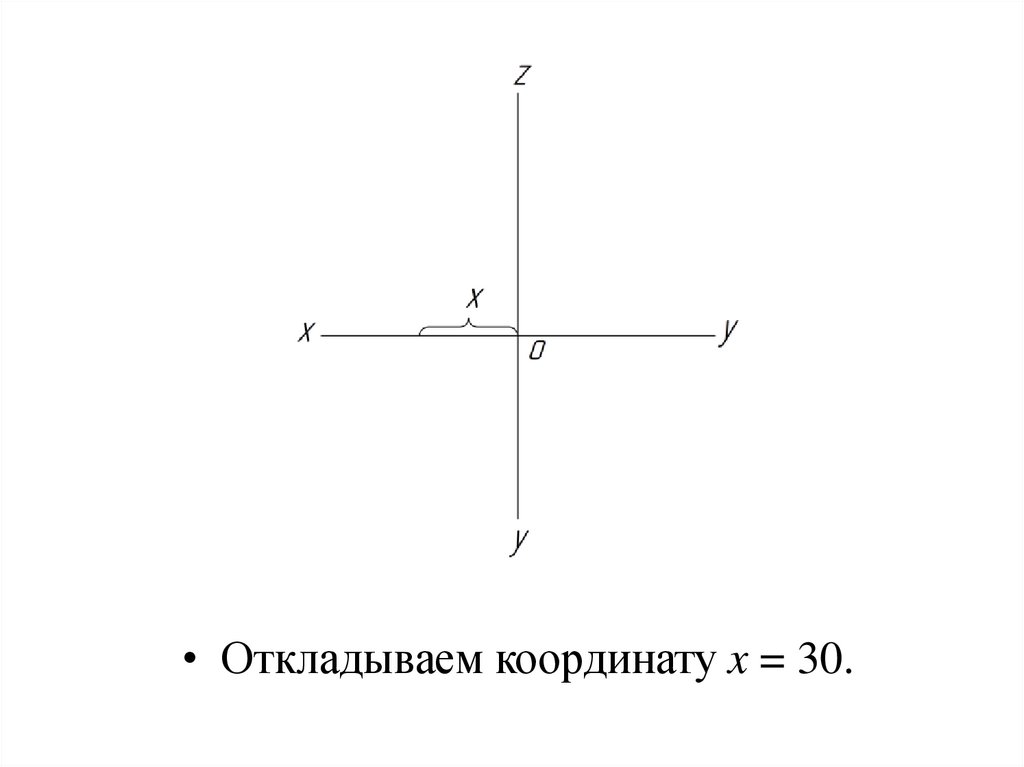
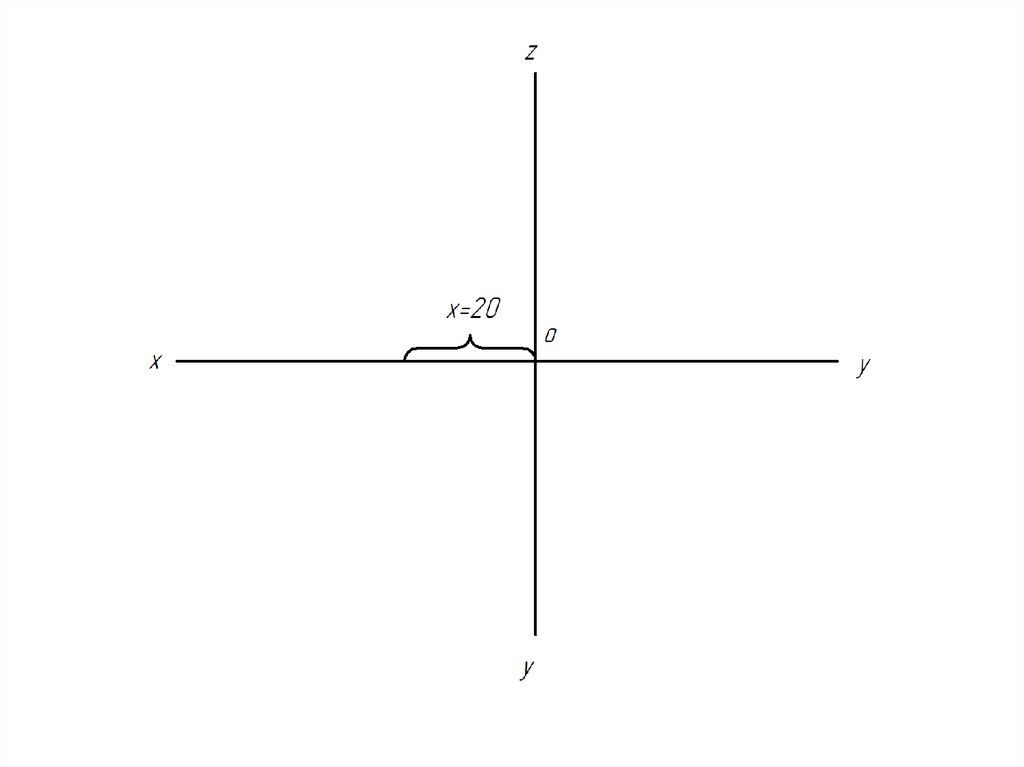
• Откладываем координату x = 30.

28.

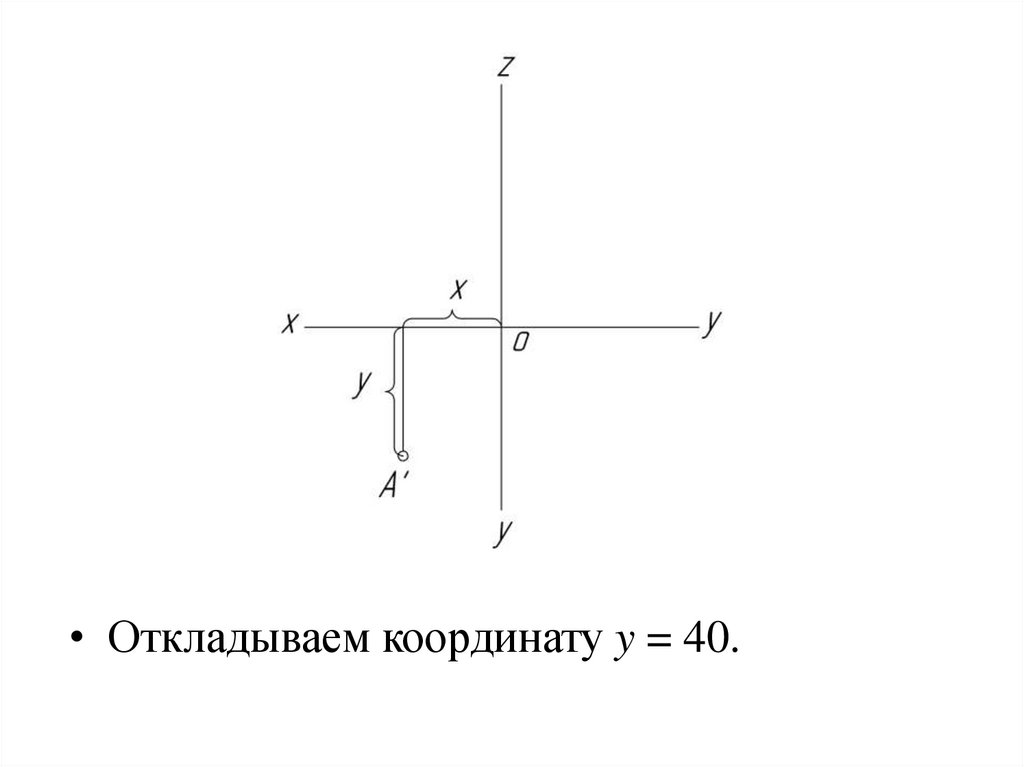
• Откладываем координату y = 40.

29.

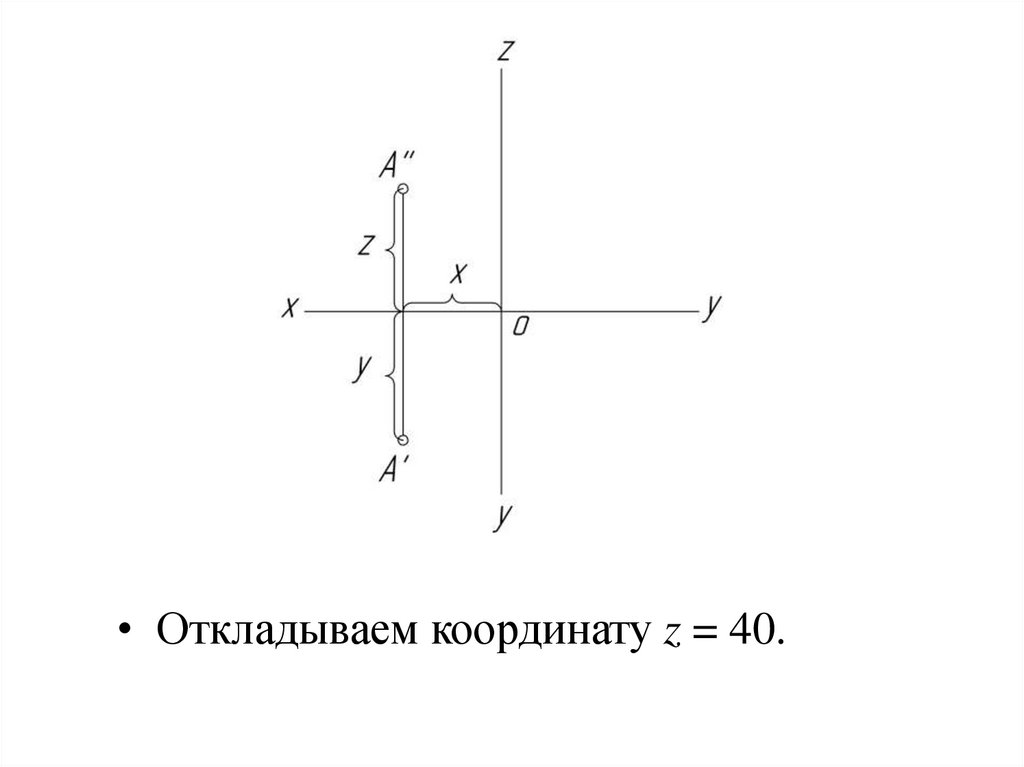
• Откладываем координату z = 40.

30.

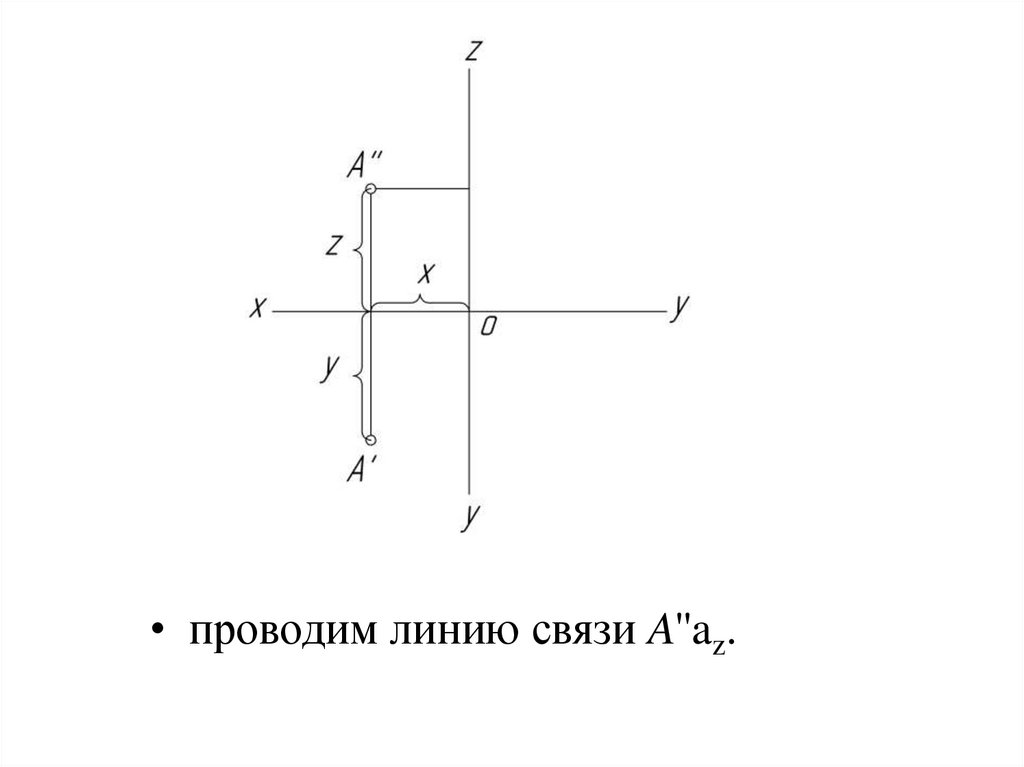
• проводим линию связи A''az.

31.

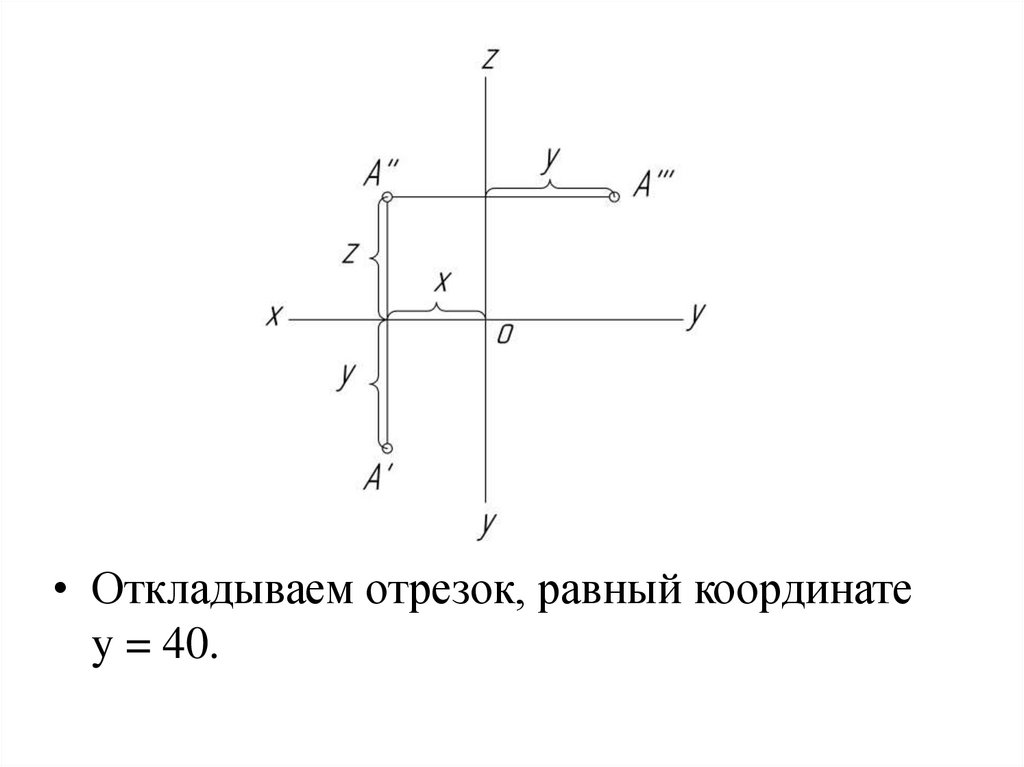
• Откладываем отрезок, равный координате
y = 40.

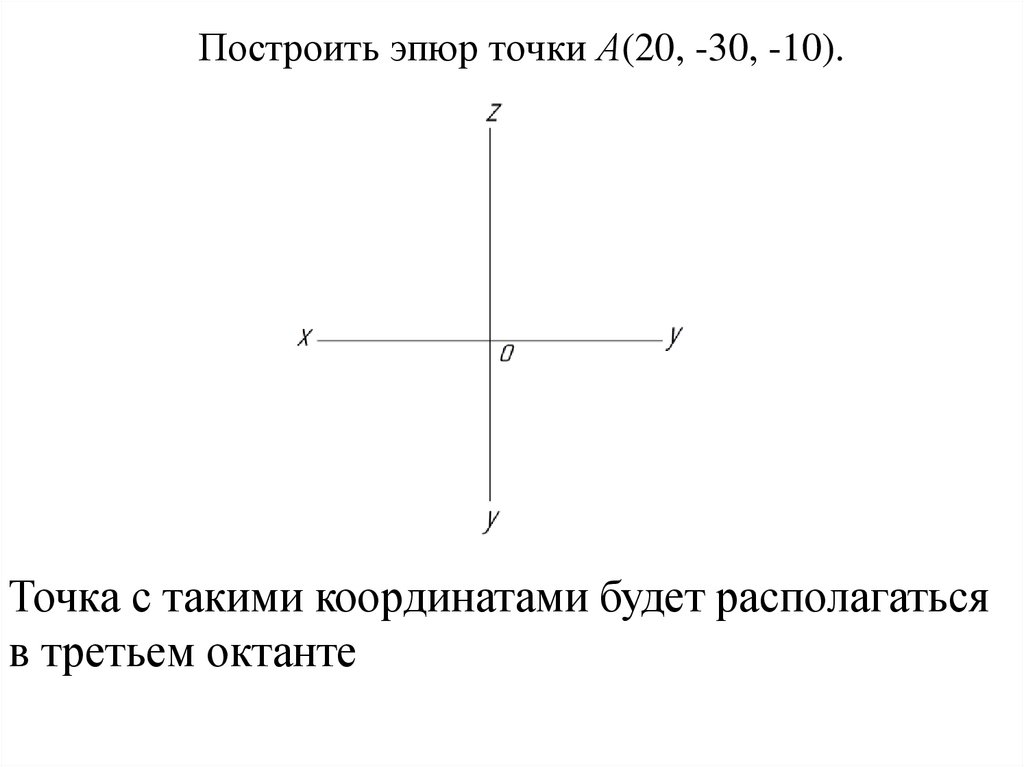
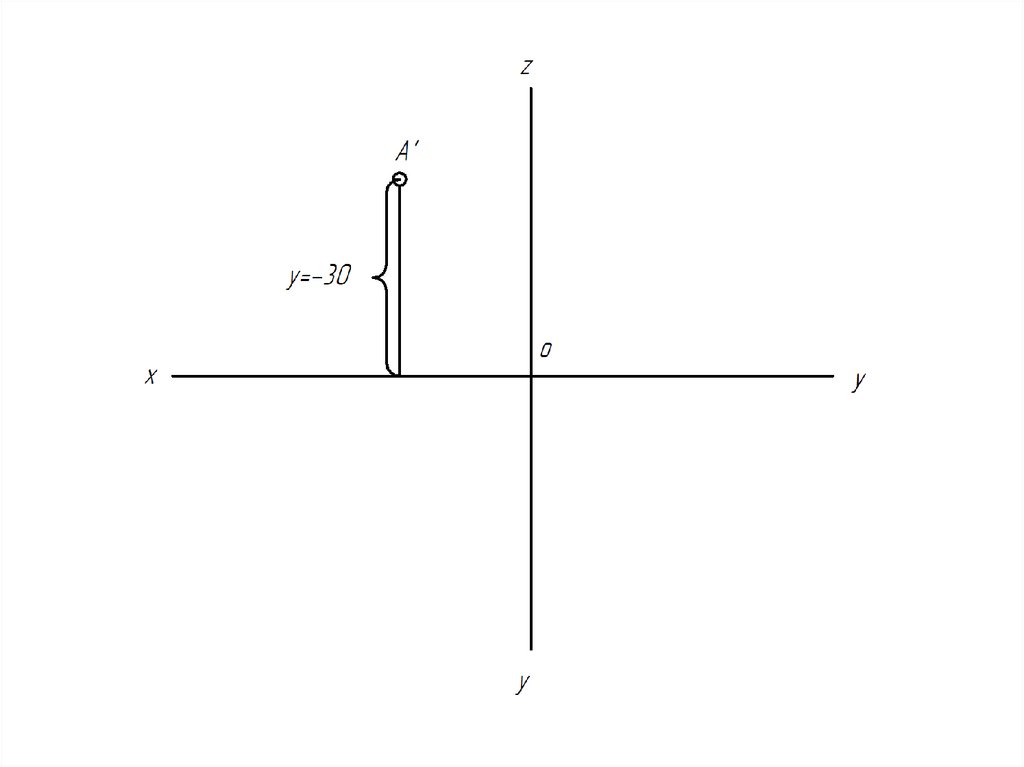
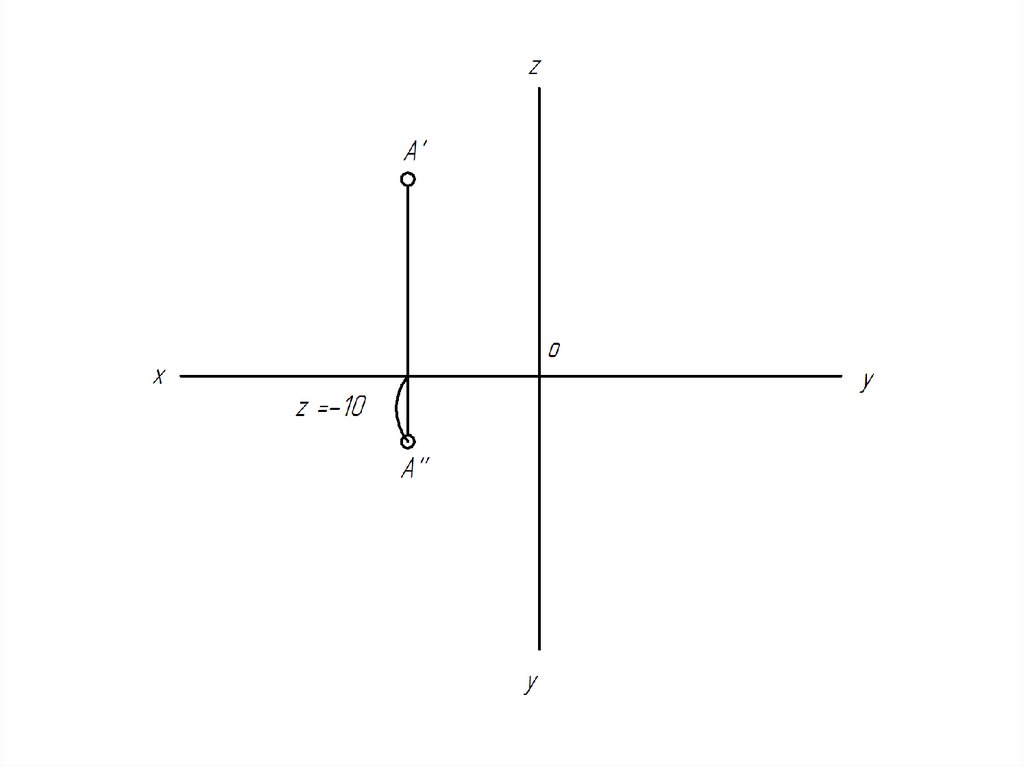
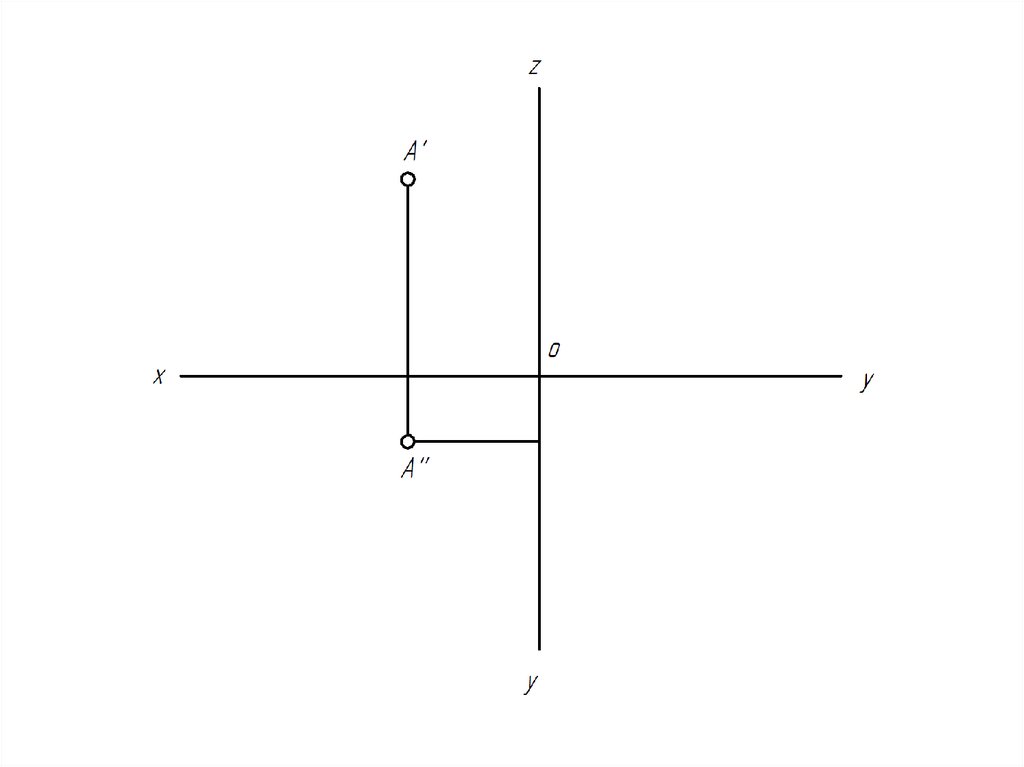
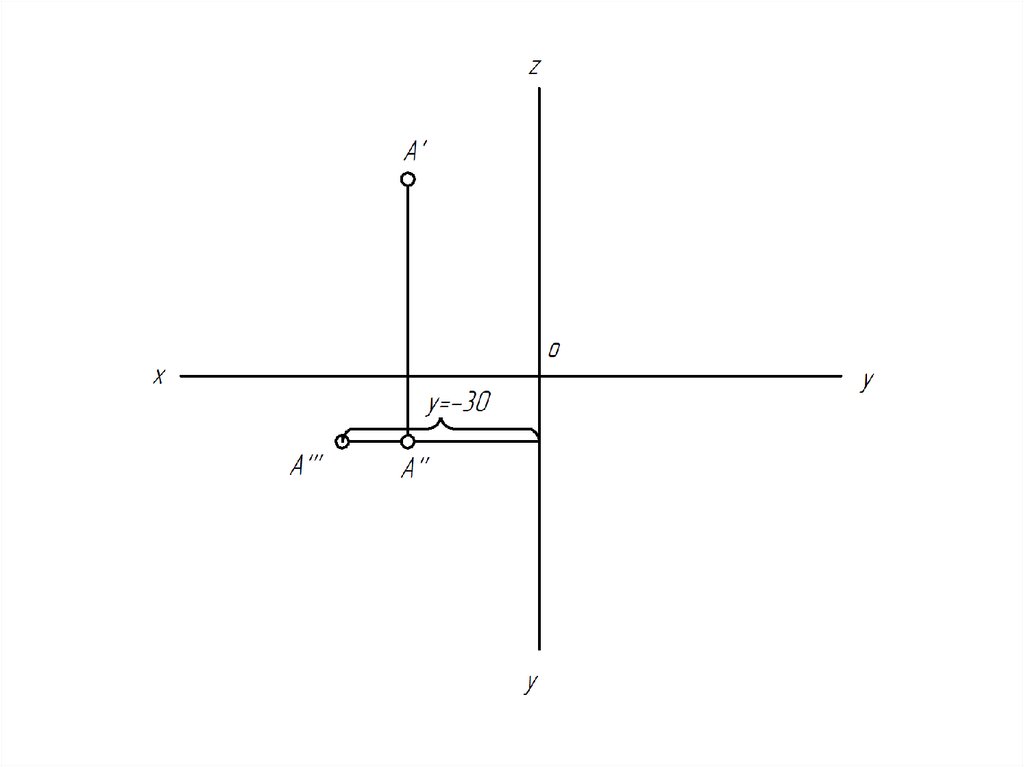
32. Построить эпюр точки А(20, -30, -10).

Точка с такими координатами будет располагаться
в третьем октанте

33.

34.

35.

36.

37.

38.

39.

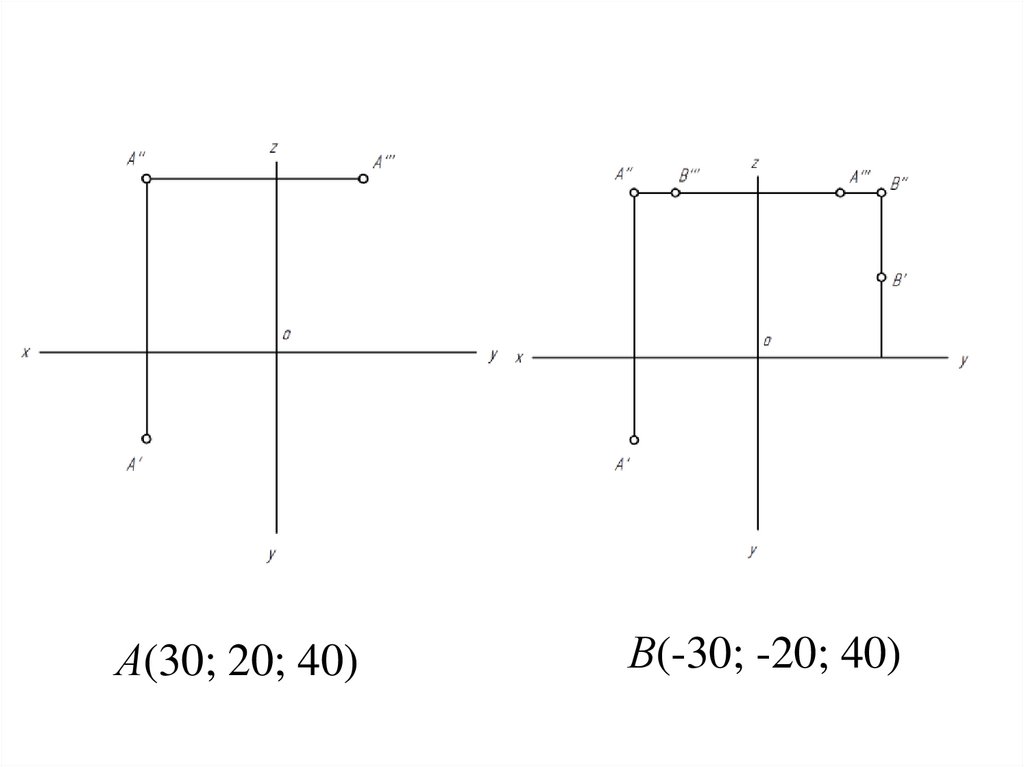
• Построить точку В, расположенную
симметрично точке А(30; 20; 40)
относительно оси z. Записать координаты
точки В.
• Точка А расположена в I октанте.
• Точка В расположится в VI октанте.
• В (-30, -20, 40).

40.

А(30; 20; 40)
В(-30; -20; 40)

41.

• Построить точку В, расположенной
симметрично точке А(40; 40; 20)
относительно оси х. Записать координаты
точки В.
• Точка А расположена в I октанте.
• Точка В расположится в III октанте.
• В(40, -40, -20).