Начертательная геометрия. Лекция 1. Введение в начертательную геометрию

1.

Уральский государственный университет путей сообщения
Кафедра
“Проектирование и эксплуатация
автомобилей”
НАЧЕРТАТЕЛЬНАЯ
ГЕОМЕТРИЯ
Пьянкова Жанна Анатольевна
канд. пед. наук, доцент кафедры
«Проектирование и эксплуатация автомобилей»
(ПиЭА)
ауд. Б1-72

2. Лекция 1. Введение в начертательную геометрию

Введение в
начертательную геометрию
Лекция 1.
• Предмет и задачи начертательной
геометрии
• Виды проецирования
• Ортогональная система плоскостей
проекций
• Ортогональные проекции точки

3.

- НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ наука о способах изображения
пространственных форм на
плоскости или другой поверхности
и методах решения геометрических
задач по этим изображениям

4. Задачи НГ:

Построение изображений объемных форм,
имеющих три измерения на плоскости,
имеющей два измерения
Чтение изображений, т.е. мысленное
представление размеров и формы
предметов, их взаимное расположение в
пространстве
Решение инженерных задач графическим
способом
Развитие пространственного воображения4

5. Проецирование – процесс получения на чертеже достоверного изображения, по которому можно представить форму и размеры объекта

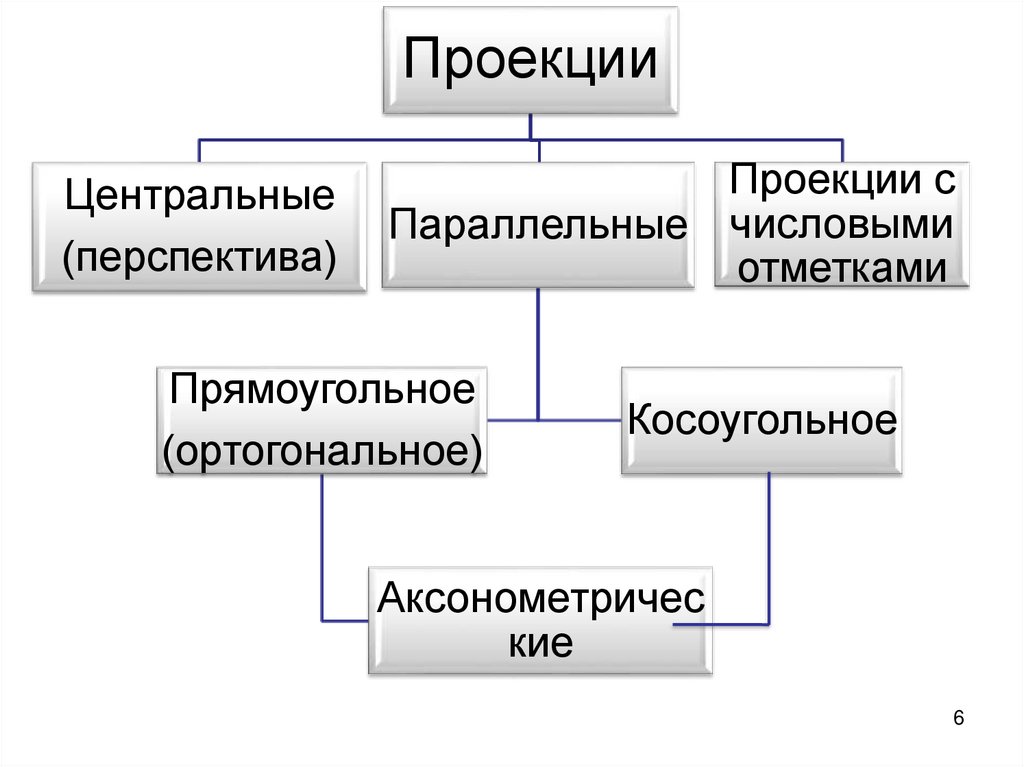
6.

Проекции
Центральные
(перспектива)
Проекции с
Параллельные числовыми
отметками
Прямоугольное
(ортогональное)
Косоугольное
Аксонометричес
кие
6

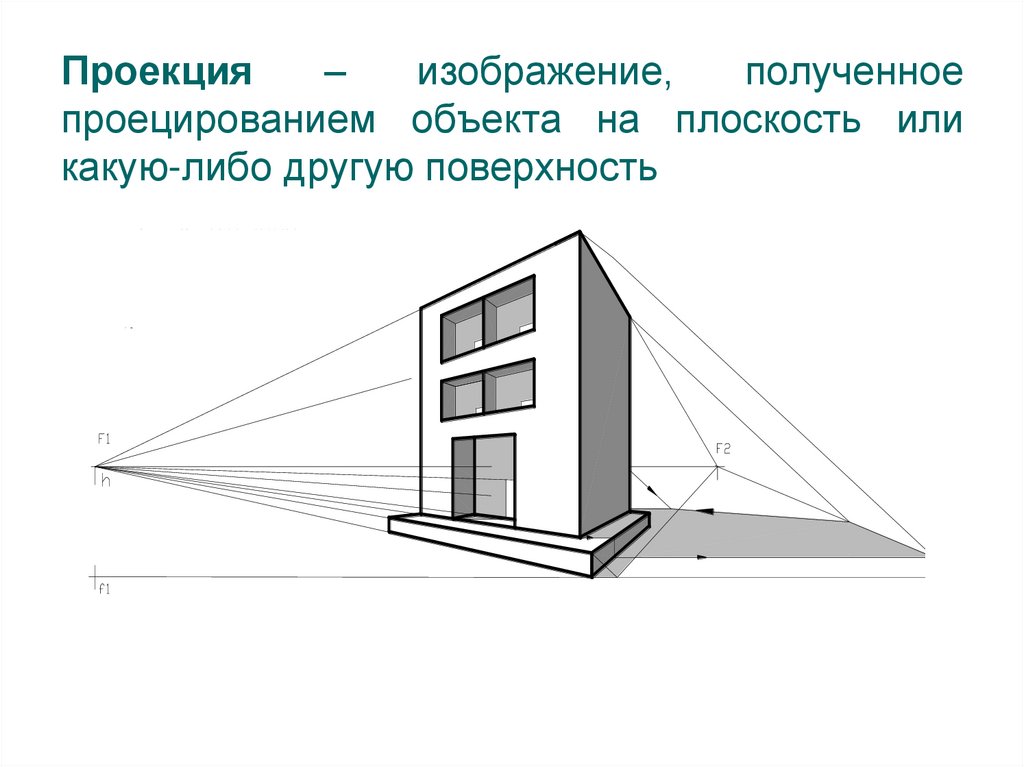
7. Проекция – изображение, полученное проецированием объекта на плоскость или какую-либо другую поверхность

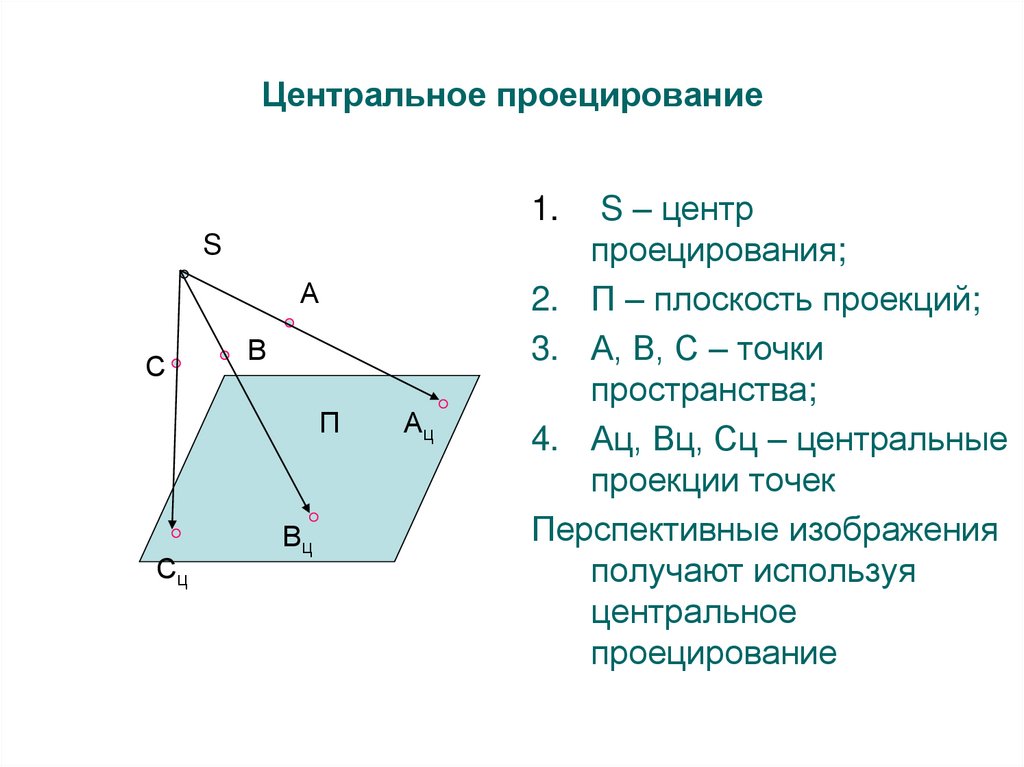
8. Центральное проецирование

S – центр
проецирования;
2. П – плоскость проекций;
3. А, В, С – точки
пространства;
4. Ац, Вц, Сц – центральные
проекции точек
Перспективные изображения
получают используя
центральное
проецирование
1.
S
А
С
В
П
Сц
Вц
Ац

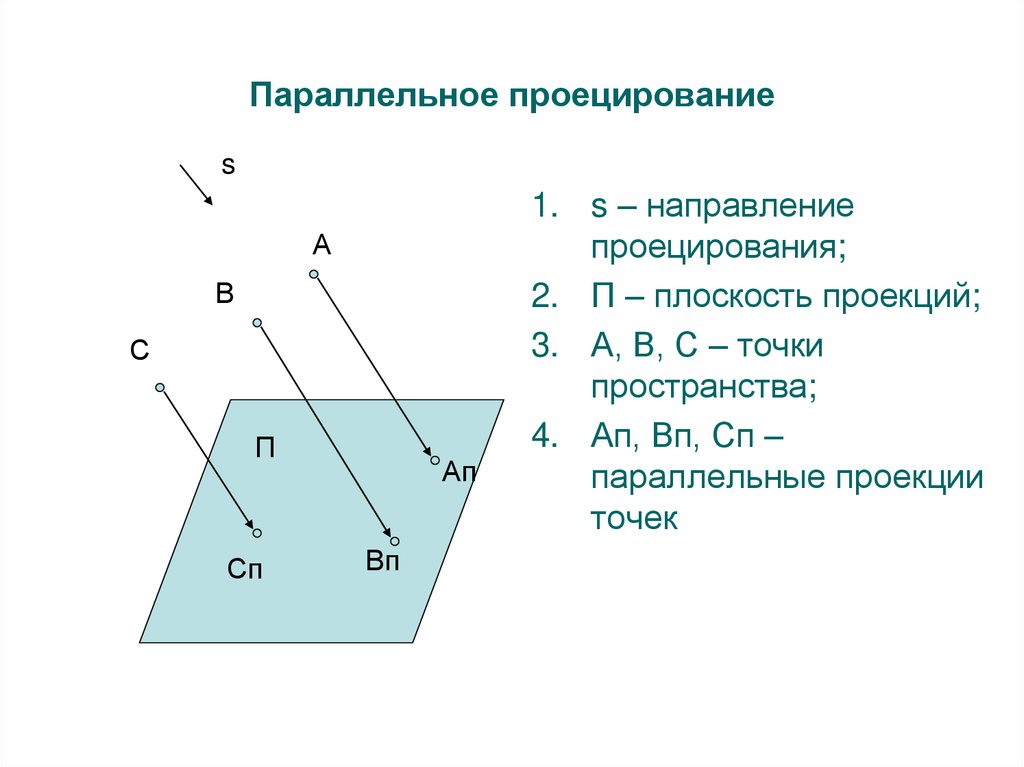
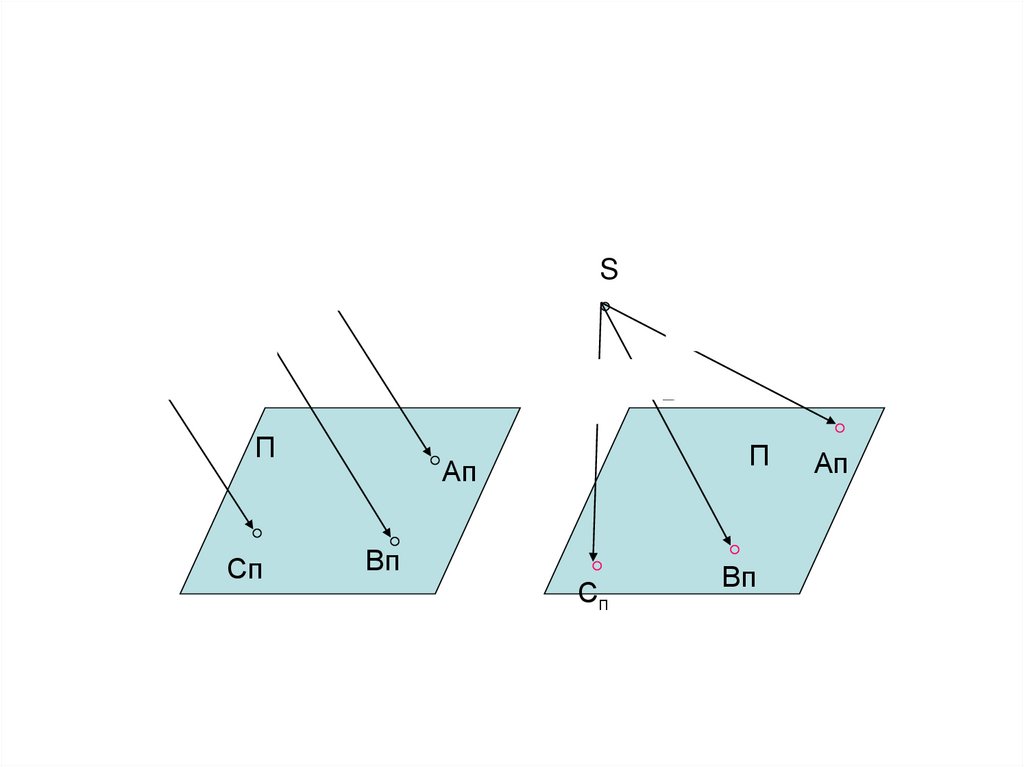
9. Параллельное проецирование

s
А
В
С
П
Сп
Ап
Вп
1. s – направление
проецирования;
2. П – плоскость проекций;
3. А, В, С – точки
пространства;
4. Ап, Вп, Сп –
параллельные проекции
точек

10. ПАРАЛЛЕЛЬНЫЕ ПРОЕКЦИИ:

Прямоугольные – если
проецирующие лучи направлены к
плоскости проекций под прямым
углом
Косоугольные - если
проецирующие лучи направлены к
плоскости проекций под углом, не
равным прямому
10

11. Ортогональное проецирование

А
s
В
С
Ап
Сп
Вп
П
1.Направление проецирования - s;
2. Плоскость проекций - П ;
S┴П
3. Точки пространства
А, В, С;
4. Ортогональные проекции
точек - Ап, Вп, Сп
ОРТО- с греческого
переводится как прямой
угол

12.

S
А
А
В
С
С
П
Сп
В
П
Ап
Вп
Сп
Вп
Ап

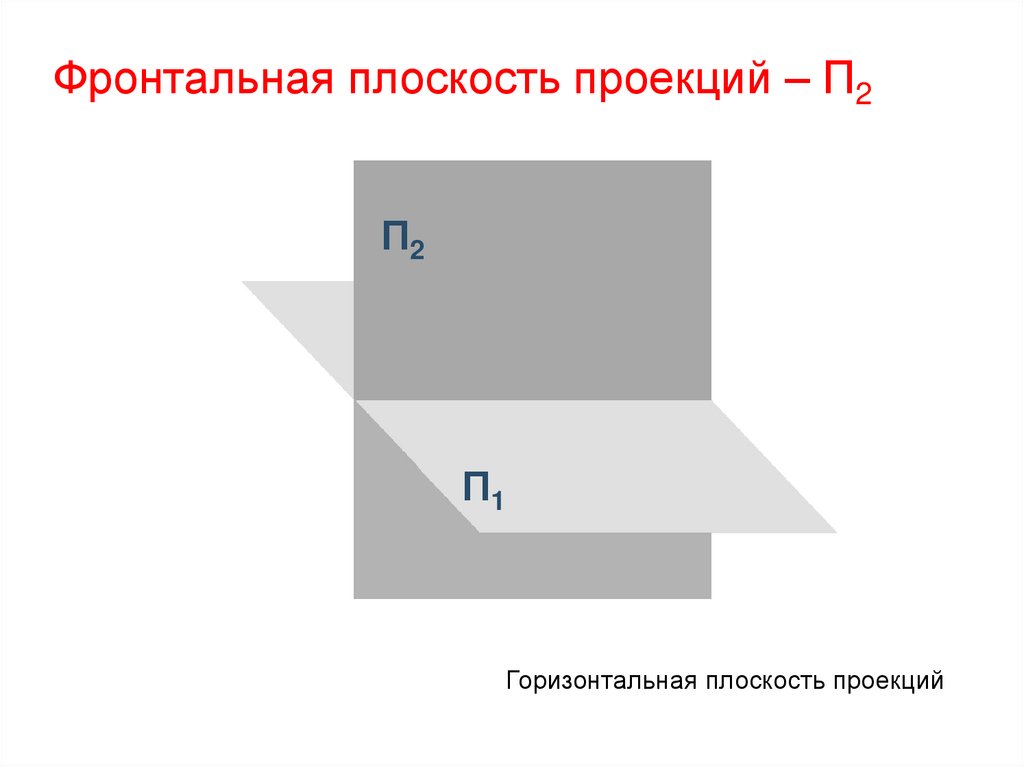
13. Формирование ортогональной системы плоскостей и осей координат

П1
Горизонтальная плоскость проекций - П1

14.

Фронтальная плоскость проекций – П2
П2
П1
Горизонтальная плоскость проекций

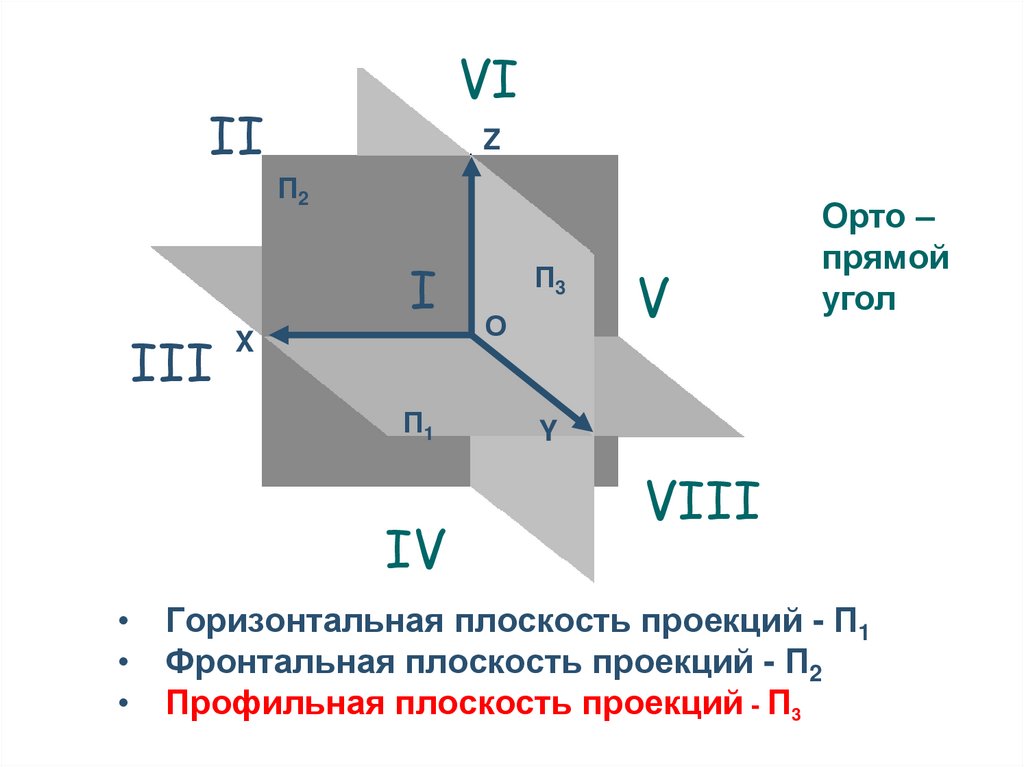
15.

VI
ІI
Z
П2
І
ІII
X
П1
IV
П3
О
V
Орто –
прямой
угол
Y
VIII
Горизонтальная плоскость проекций - П1
Фронтальная плоскость проекций - П2
Профильная плоскость проекций - П3

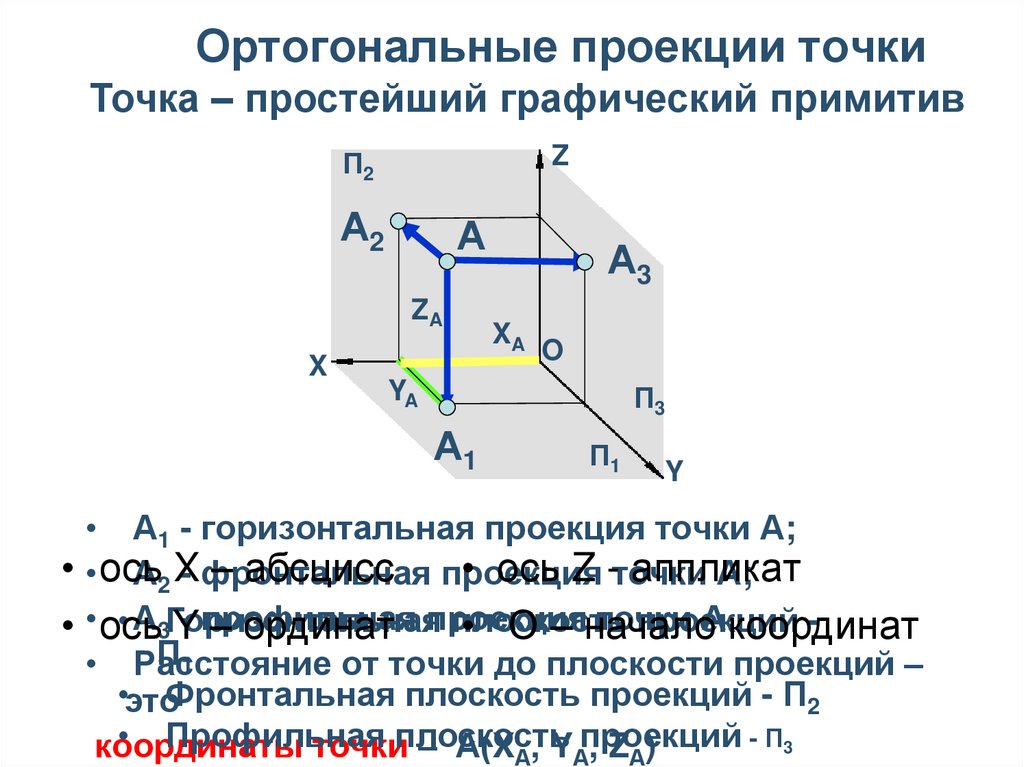
16. Ортогональные проекции точки

Точка – простейший графический примитив
Z
П2
А2
А
ZA
X
А3
XA
O
YA
П3
А1
П1
Y
• А1 - горизонтальная проекция точки А;
• • ось
– абсцисс проекция
• ось Z -точки
аппликат
А2 X
- фронтальная
А;
точки
А.координат
• А3Горизонтальная
плоскость
проекций
• • ось
Y- профильная
– ординат проекция
• О – начало
П1
• Расстояние
от точки до плоскости проекций –
•этоФронтальная плоскость проекций - П2
• Профильная
- П3
координаты
точкиплоскость
– А(XА, YАпроекций
, ZА)

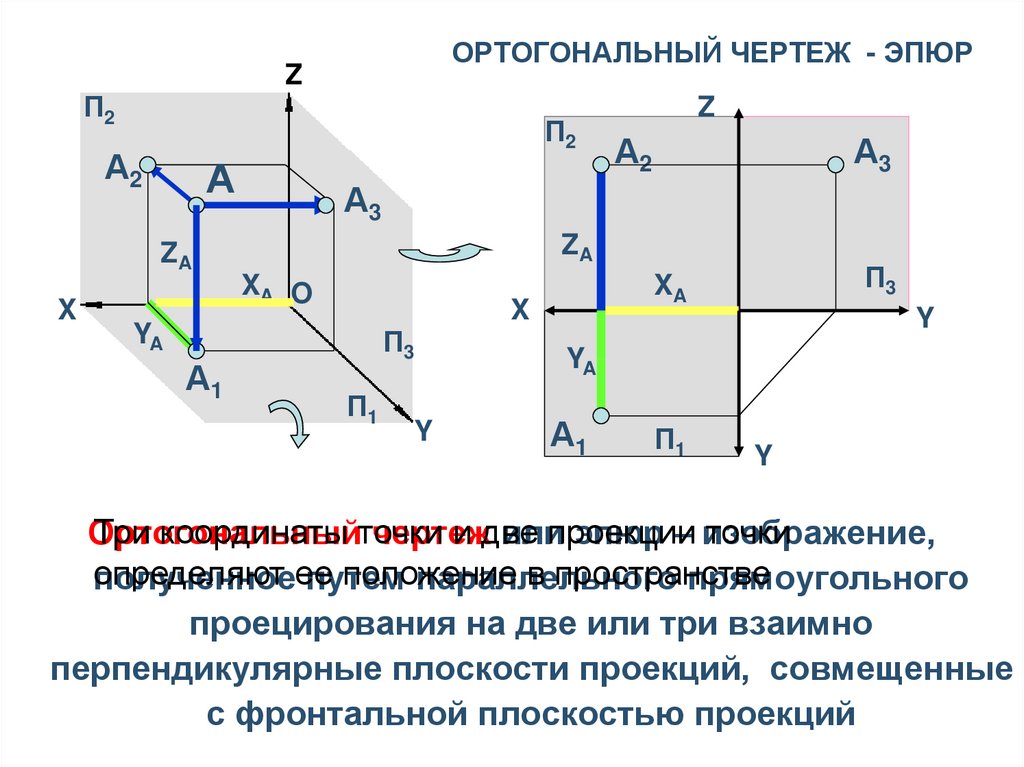
17. ОРТОГОНАЛЬНЫЙ ЧЕРТЕЖ - ЭПЮР

Z
П2
П2
А2
А
А3
ZA
XA O
П3
П1
Y
П3
XA
X
YA
А1
А2
А3
ZA
X
Z
Y
YA
А1
П1
Y
Три координаты точки
и две
точки
Ортогональный
чертеж
илипроекции
эпюр – изображение,
определяют
положение
в пространстве
полученноеее
путем
параллельного
прямоугольного
проецирования на две или три взаимно
перпендикулярные плоскости проекций, совмещенные
с фронтальной плоскостью проекций

18. Понятие о четвертях и октантах

Четверть – двугранный угол, образованный
в пересечении плоскостей П1 и П2
Октант – это трехгранный угол, образованный
в пересечении плоскостей П1, П2, П3
Ортогональные проекции это
–
прямоугольные проекции на взаимно
перпендикулярных плоскостях проекций
18

19. СВОЙСТВА ОРТОГОНАЛЬНЫХ ПРОЕЦИЙ ТОЧКИ:

Две разноименные проекции точки
расположены на одной линии связи
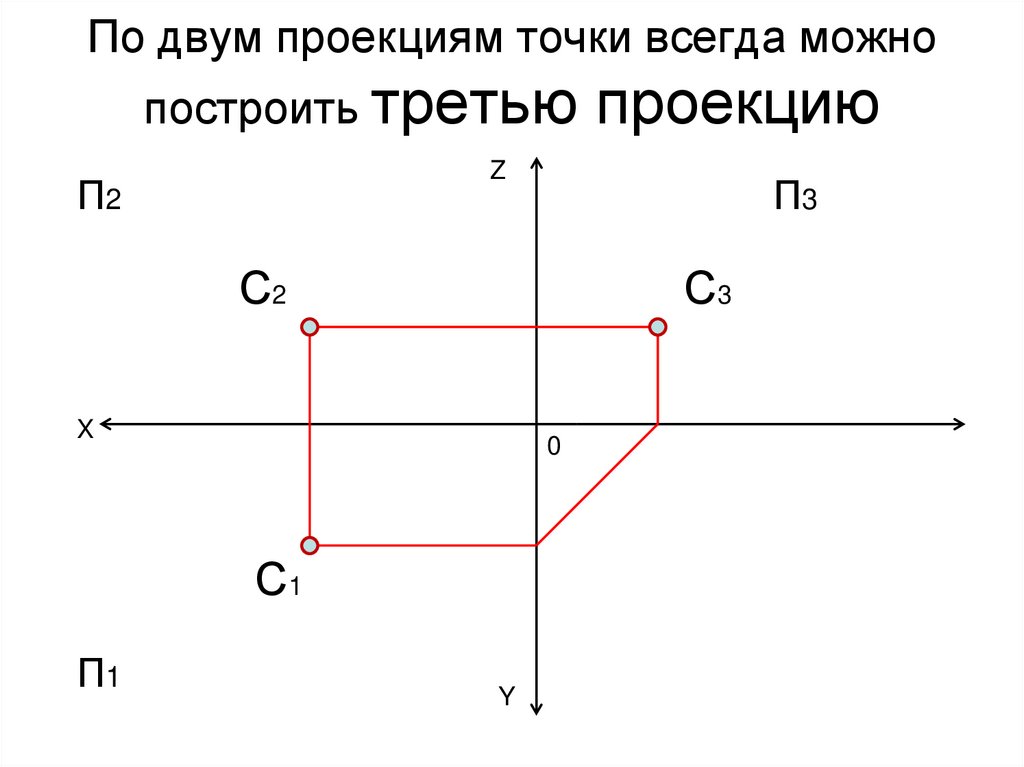
По двум проекциям точки всегда
можно построить недостающую
третью проекцию
По двум проекциям точки всегда
можно определить положение
самой точки в пространстве
19

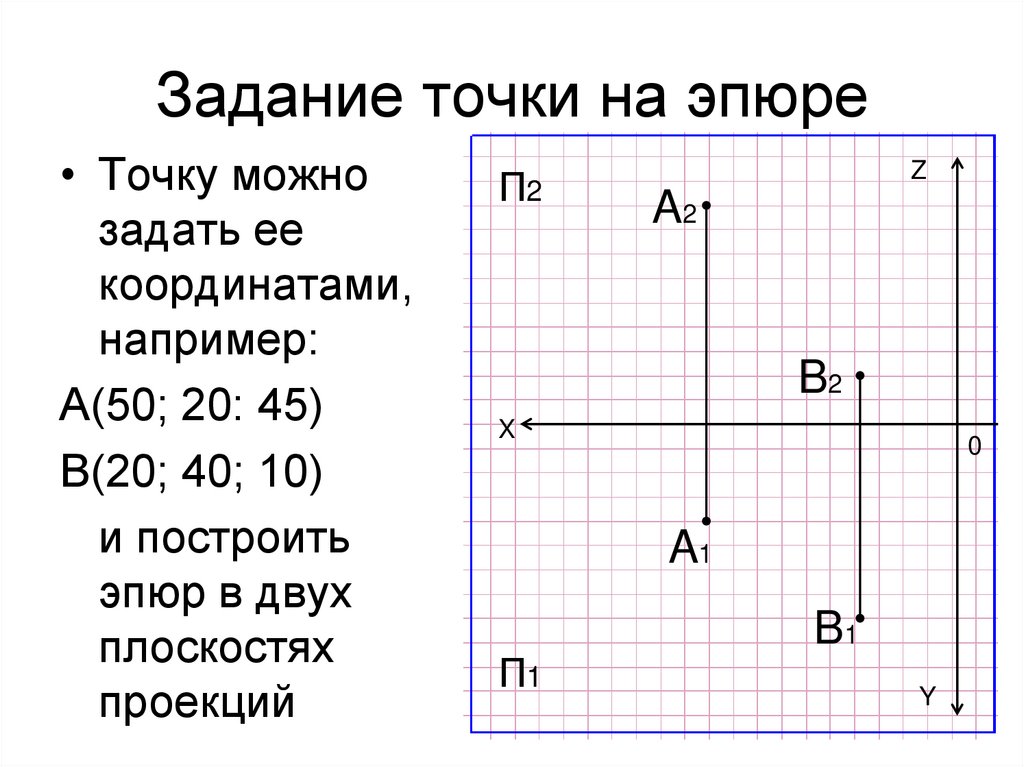
20. Задание точки на эпюре

• Точку можно
задать ее
координатами,
например:
А(50; 20: 45)
В(20; 40; 10)
и построить
эпюр в двух
плоскостях
проекций
П2
Z
A2
B2
X
0
A1
П1
B1
Y

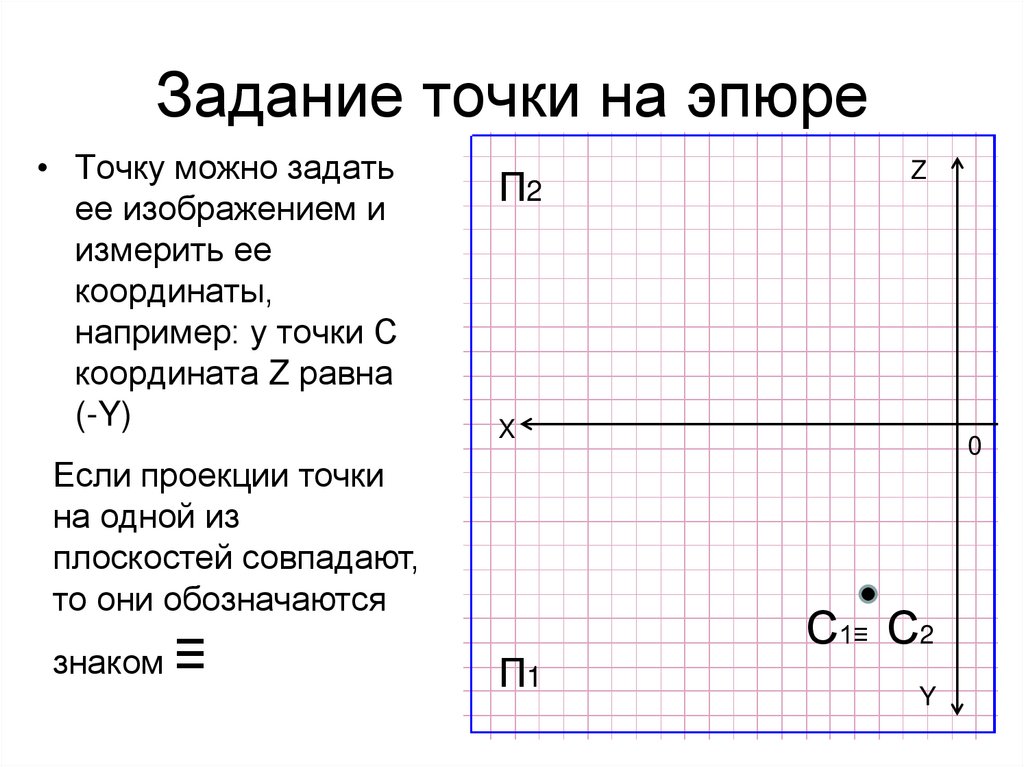
21. Задание точки на эпюре

• Точку можно задать
ее изображением и
измерить ее
координаты,
например: у точки С
координата Z равна
(-Y)
П2
X
Если проекции точки
на одной из
плоскостей совпадают,
то они обозначаются
знаком
≡
Z
П1
0
С1≡ С2
Y

22. Задание точки на эпюре

• Точку можно
задать ее
положением
относительно
плоскостей
проекций,
например:
• D отстоит от П1
на 35мм, а от П2
и П3 на 60мм
Z
П2
D2
X
П1
0
D1
Y

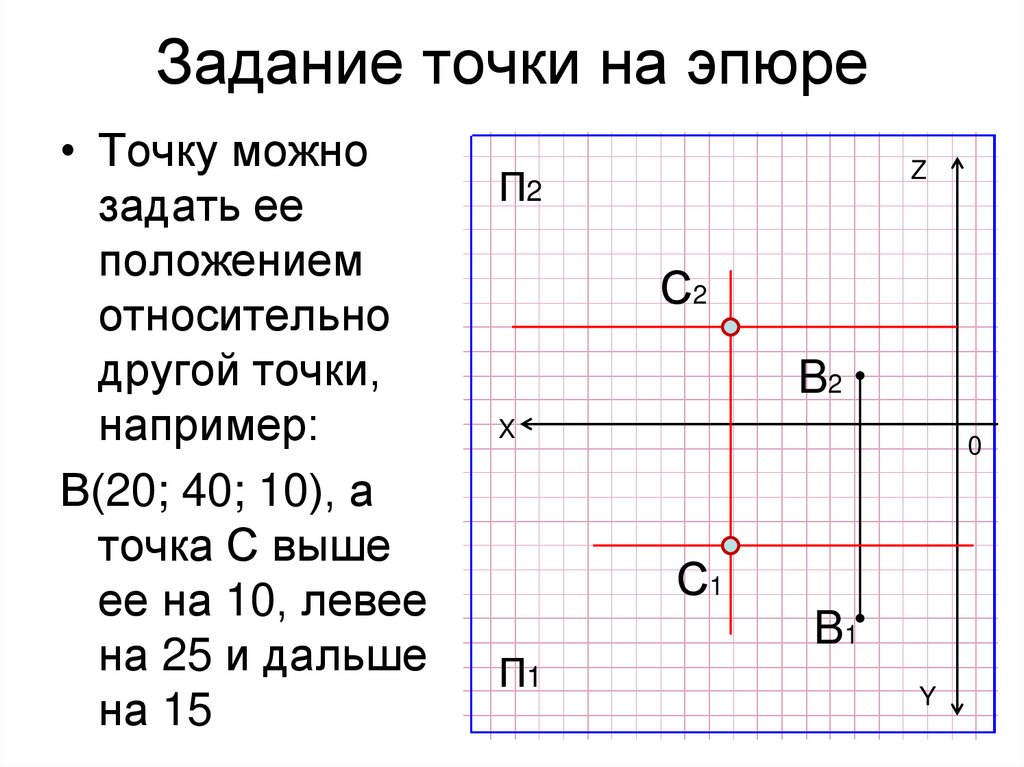
23. Задание точки на эпюре

• Точку можно
задать ее
положением
относительно
другой точки,
например:
В(20; 40; 10), а
точка С выше
ее на 10, левее
на 25 и дальше
на 15
Z
П2
С2
B2
X
0
С1
П1
B1
Y

24. По двум проекциям точки всегда можно построить третью проекцию

Z
П2
П3
С2
С3
X
0
С1
П1
Y

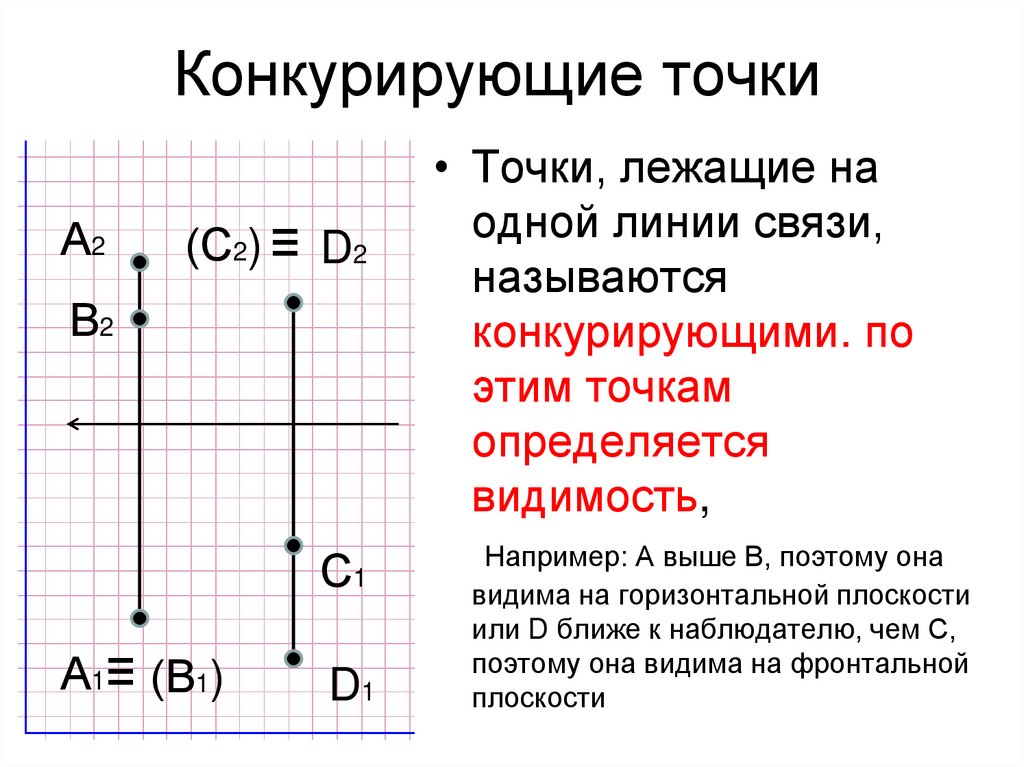
25. Конкурирующие точки

А2
(С2) ≡ D2
В2
С1
А1≡ (В1)
D1
• Точки, лежащие на
одной линии связи,
называются
конкурирующими. по
этим точкам
определяется
видимость,
Например: А выше В, поэтому она
видима на горизонтальной плоскости
или D ближе к наблюдателю, чем С,
поэтому она видима на фронтальной
плоскости

26. Спасибо за внимание!