Похожие презентации:
Обратная матрица. Система линейных алгебраических уравнений. Лекция 2
1.
МеждународнаяДисциплина
образовательная
«Математика 1»
корпорация
Обратная матрица.
Система линейных
алгебраических
уравнений
Лекция 2
Буганова Светлана Николаевна
2023-2024 учебный год
2.
План лекции1. Понятие обратной матрицы.
2. Алгоритм нахождения обратной матрицы.
3. Системы линейных алгебраических
уравнений (СЛАУ).
4. Методы решения СЛАУ.
- Метод Крамера;
- Матричный метод (с помощью обратной
матрицы)
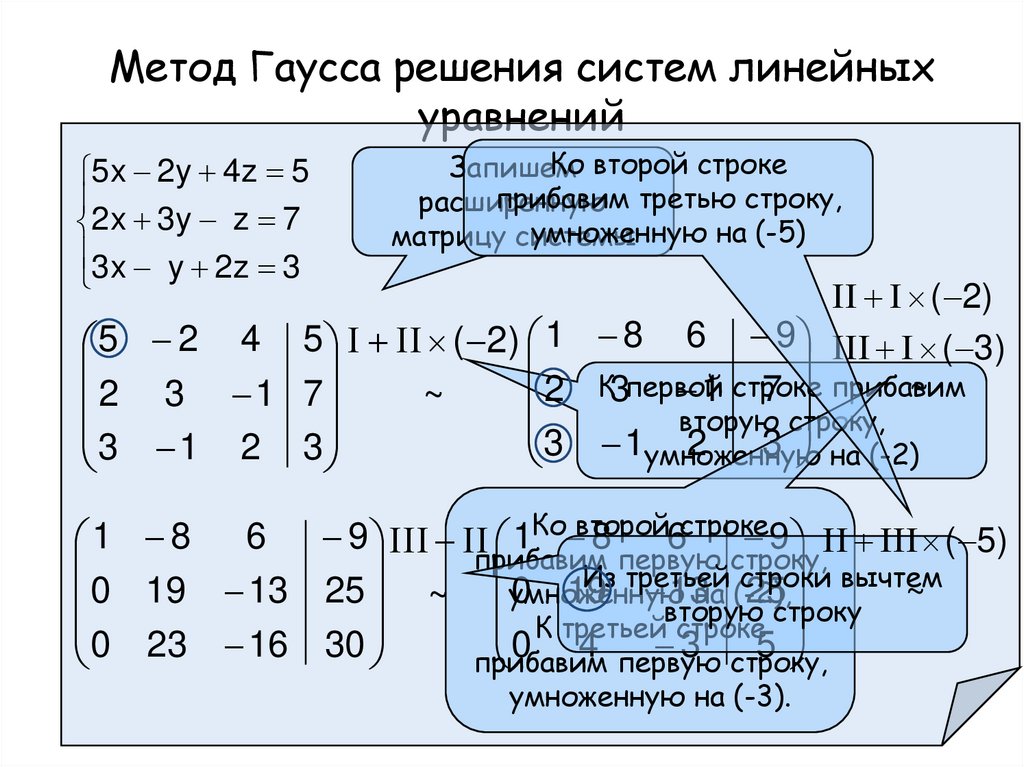
- Метод Гаусса
2
3.
Матрица A-1 называется обратной кматрице А, если
АA-1=A-1А=Е
где Е – единичная матрица
4.
1Определяем, квадратная ли
матрица. Если нет, то
обратной матрицы для
нее не существует.
5.
2Вычисляем определитель.
Он должен быть отличным от нуля
6.
3Заменяем каждый элемент матрицы
его алгебраическим дополнением.
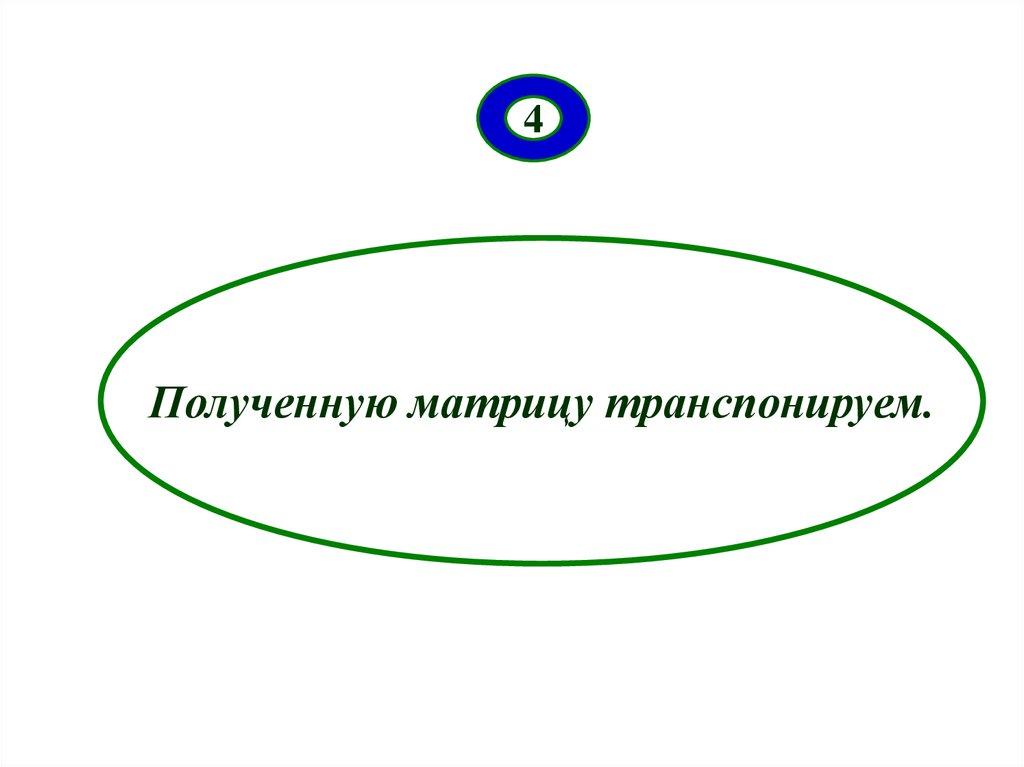
7.
4Полученную матрицу транспонируем.
8.
5Каждый элемент полученной
матрицы делим на определитель
исходной матрицы. Получаем
матрицу, обратную к данной.
9.
6Делаем проверку. Для этого
перемножаем полученную и исходную
матрицы. Должна получиться
единичная матрица.
10.
Найти матрицу, обратную к матрице2 1
A
3 2
11.
Применяем алгоритмматрицы.
нахождения
обратной
1
Матрица
квадратная,
следовательно
обратная матрица для нее существует.
2
Находим определитель:
2 1
A
2 2 3 1 1 0
3 2
12.
3Находим алгебраические дополнения
каждого элемента матрицы:
A11 ( 1) M 11 2
2
A12 ( 1) M12 3
3
A21 ( 1)3 M 21 1





























 Математика
Математика








