Теплопроводность. Задачи

1.

Задание 1. Определить коэффициент теплопроводности кирпичной стенки печи
толщиной 380 мм температура на внутренней стенке 300°С и на наружной 45°С.
Потери теплоты через стенку 200 Вт/м2.
Решение
Коэффициент теплопроводности можно найти из закона Фурье:
dt
Q F
dx
Q
q
F
q
dt dx
Заменяя бесконечно малые приращения конечными, получим:
q x
t
t t 2 t1
Подставим числовые значения и получим:
0,30 Вт/(°С∙м)

2.

Задание 2. Определить значение коэффициента теплопроводности материала
стенки, если при толщине 30 мм и температурном напоре t 30 C плотность
теплового потока q 100 Вт/м 2 .
Решение
Используем закон Фурье:
q
dt
t
dx
Выразим отсюда коэффициент теплопроводности
q
t
Подставим числовые значения
0,03 м
100 Вт/м
0,1 Вт/(м С)
30 C
2

3.

Задание 3. Через металлическую стенку печи толщиной 14 мм от газов к кипящей
воде проходит удельный тепловой поток 25000 Вт/м2. Коэффициент
теплопроводности стали 50 Вт/(м∙К). Определить температурный перепад на
поверхности стенки.
Решение
Используем закон Фурье:
dt
t
q
dx
x
Получим выражение для определения температурного перепада :
q x
t
Подставим числовые значения и получим:
7°С

4.

Задание 4. Определить плотность теплового потока через бетонную стену
толщиной 300 мм , если температура на внутренней стенке t1 20 C
и на
наружной t 2 10 C . Коэффициент теплопроводности бетона 1,0 Вт/(м К) .
Решение
Плотность теплового потока можно найти из закона Фурье:
t 2 t1
t1 t 2
q
Подставим числовые значения и получим:
100 Вт/м2

5.

Задание 5. Слой льда на поверхности воды имеет толщину л 250 мм .
Температура на нижней и верхней поверхностях соответственно t1л 0 C
и t 2л 15 C . Определить плотность теплового потока, если коэффициент
теплопроводности льда л 2,25 Вт/(м К). Как изменится плотность теплового
потока, если лед покроется слоем снега толщиной с 150 мм и температура на
поверхности снега будет t 2с 20 C . Коэффициент теплопроводности снега
с 0,45 Вт/(м К).
Решение
Плотность теплового потока через слой льда можно найти из закона Фурье:
t1л t 2л
qл л
л
Подставим числовые значения и получим: q л 135 Вт/м 2
Если слой льда покроется слоем снега, то плотности теплового потока через слой
льда и снега можно найти через многослойную стенку:
t1л t 2с
q
с л
с л
Подставим числовые значения и получим 45 Вт/м2.

6.

Задача 6. Стенка из шлакобетона имеет размеры: длина a 20 м , высота h 3,5 м
и толщина 0,5 м. Теплопроводность материала 0,9 Вт/(м К). Температура
на внутренней поверхности стенки t1 18 C и на наружной t 2 15 C . Определить
плотность теплового потока и тепловой поток, а также суточное количество
теплоты, проходящей через стенку (МДж).
Решение
Плотность теплового потока через стенку можно найти из закона Фурье:
t t
q 1 2
18 C ( 15 C )
59,4 Вт/м 2
Подставим числовые значения q
0,5 м
0,9 Вт/(м К)
Тепловой поток определим по формуле:
Q qF qah
4158 Вт
Суточный расход количества теплоты будет равен: W Q qah
Подставим числовые значения:
W 4158 Вт 24 3600 с 359 106 Дж 359 МДж

7.

Задача 7. Определить максимальную толщину образования льда, если его
теплопроводность 2,25 Вт/(м К) , температура на глубине 0,5 м t1 5 C ,
а на верхней поверхности t 2 15 C.
Решение
Плотность теплового потока при глубине 0,5 м можно найти из закона Фурье:
t1 t 2
q
Максимальная толщина льда будет иметь место тогда, когда на глубине
температура составит t1 0 C .
(t1 t 2 )
max
q
Подставив сюда выражение для плотности теплового потока, получим:
t1 t 2
max
t1 t 2
Подставим числовые значения
max 0,5 м
0 C ( 15 C )
0,75 м
5 C ( 15 C )

8.

Задача 8. Определить температуру на внутренней поверхности слоя изоляции
толщиной 0,25 м, если температура внутри слоя изоляции на глубине
1 0,05 м составляет t1 75 C , при этом на наружной поверхности
обеспечивается t 2 45 C .
Решение
Плотность теплового потока на участке толщиной 0,05 м можно найти из закона
Фурье:
t1 t 2
q1
1
Плотность теплового потока по всей толщине изоляции:
t1 t 2
q
Очевидно, что q1 q . Тогда
t1 t 2 t1 t 2
1
(t1 t 2 ) 1 (t1 t 2 )
Отсюда температура на внутренней поверхности слоя изоляции толщиной 0,25 м

9.

t1 (t1 t 2 ) t 2
1
Подставим числовые значения:
0,25
t1
(75 45) 45 195 C
0,05

10.

Задача 9. Определить плотность теплового потока через плоскую шамотную
стенку толщиной 0,5 м и найти действительное распределение температуры,
если на наружных поверхностях температуры соответственно t1 1000 C, t 2 0 C
и коэффициент теплопроводности шамота 1,0 (1 0,001t ) Вт/(м С) .
Решение
Плотность теплового потока при переменном коэффициенте теплопроводности
определим по формуле:
Подставим числовые значения:
1
1000 0
2
q
1 0,001
(1000
0)
3000
Вт/м
0,5
2
Уравнение температурной кривой в этом случае имеет вид:
Подставим числовые значения и получим распределение температур внутри
стенки:

11.

x, см
0
10
20
30
40
50
t, °С
1000
844
673
483
265
0

12.

Задача 10. Определить плотность теплового потока, проходящего через стенку
котла, если толщина её 1= 20 мм, коэффициент теплопроводности материала 1=
= 50 Вт/(м∙°С) и с внутренней стороны стенка покрыта слоем котельной накипи
толщиной 2= 2 мм с коэффициентом теплопроводности 2= 1,0 Вт/(м∙°С).
Температура наружной поверхности t1= 250°С, а внутренней − t3= 200°С.
Решение
q
t1 t 3
1 2
1 2
250 200
q
20830 Вт/м 2
0,02 0,002
50
1

13.

Задача 11. Паропровод диаметром 160/170 мм покрыт двуслойной изоляцией.
Толщина первого слоя 2= 30 мм и второго 3= 50 мм. Коэффициенты
теплопроводности трубы и изоляции соответственно равны: 1= 50 Вт/(м∙°С), 2=
0,15 Вт/(м∙°С) и 3= 0,08 Вт/(м∙°С). Температура внутренней поверхности
паропровода t1= 300°С и внешней поверхности изоляции t4= 50°С. Определить
линейную плотность теплового потока и температуры на поверхностях раздела
отдельных слоёв.
Решение
2 (t1 t 4 )
ql
1 d2 1 d3 1 d 4
ln ln ln
1 d1 2 d 2 3 d 3
d 3 170 2 30 230 мм
ql
d 3 d 2 2 2
d 4 d 3 2 3
d 4 230 2 50 330 мм
2 3,14 (300 50)
240 Вт/м
1
1
1
0,17
0,23
0,33
ln
ln
ln
50 0,16 0,15 0,17 0,08 0,23

14.

Теперь рассчитаем температуры на границах отдельных слоёв
d2
ql
t 2 t1
ln
2 1 d1
240
0,17
t 2 300
ln
300 C
2 3,14 50 0,16
d4
ql
t3 t 4
ln
2 3 d 3
t 4 50
240
0,33
ln
223 C
2 3,14 0,08 0,23

15.

Задача 12. Паропровод диаметром 160/170 мм покрыт двуслойной изоляцией.
Толщина первого слоя 2= 30 мм и второго 3= 50 мм. Коэффициенты
теплопроводности трубы и изоляции соответственно равны: 1= 50 Вт/(м∙°С), 2=
0,15 Вт/(м∙°С) и 3= 0,08 Вт/(м∙°С). Температура внутренней поверхности
паропровода t1= 300°С и внешней поверхности изоляции t4= 50°С. Определить
линейную плотность теплового потока и температуры на поверхностях раздела
отдельных слоёв. Задачу решить по упрощённой формуле.
Решение
Так как для всех трёх слоёв di+1/di < 2, то можно принять, что = 1. Тогда
согласно условию имеем:
dm1 165 мм
dm 2 200 мм
dm 3 280 мм
Запишем упрощённую формулу для определения линейной плотности теплового
потока:
(t1 t 4 )
ql
1 1 2 1
1
3
1 dm1 2 dm 2 3 dm 3
ql
3,14 (300 50)
243 Вт/м
0,005 1
0,03 1 0,05 1
50 0,165 0,15 0,2 0,08 0,28

16.

243
0,17
t 2 300
ln
300 C
2 3,14 50 0,16
243
0,33
t 3 50
ln
225 C
2 3,14 0,08 0,23
Таким образом, пренебрежение влиянием кривизны стенки в этом случае вносит
ошибку около 1%.

17.

Задача 13. Определить тепловой поток через стенку вращающегося
шарообразного варочного котла, внутренний диаметр которого d1= 1,2 м, а общая
толщина стенки котла и слоя изоляции = 100 мм. Температура внутренней
поверхности t1= 140°С, внешней − t2= 40°С, эквивалентный коэффициент
теплопроводности = 0,1 Вт/(м∙°С).
Решение
Тепловой поток через шарообразную стенку определим по формуле:
d1d 2
Q эк (t1 t 2 )
Внешний диаметр стенки равен: d 2 d1 2
d (d 2 )
Q эк (t1 t 2 ) 1 1
Подставим числовые значения:
Q 3,14 0,1 (140 40)
1,2 (1,2 2 0,1)
528 Вт
0,1

18.

Задача 14. По стержню из нержавеющей стали диаметром 10 мм проходит
электрический ток, вызывающий объёмное выделение теплоты мощностью qv=
=2,4∙107 Вт/м3. На поверхности стержня поддерживается температура tс= 30°С.
Найти температуру на оси стержня tо и плотность теплового потока на внешней
поверхности стержня, если коэффициент теплопроводности стали =15 Вт/(м∙°С).
Решение
Перепад температур на оси и поверхности стержня определим по формуле:
qvro2
to t c
4
Тогда температура на оси стержня равна:
qvro2
qv d 2
to
tc
tc
4
16
Подставим числовые значения:
2,4 107 0,012
to
30 40 C
16 15

19.

Плотность теплового потока на поверхность определим по соотношению:
1
1
q roqv dqv
2
4
Подставим числовые значения:
1
q 0,01 2,4 107 6 104 Вт/м2 60 кВт/м2
4

20.

Задача 15. Вычислить плотность теплового потока через оконное стекло
толщиной = 3 мм, если температуры его поверхностей tс1 = 1°С и tс2 = −1°С.
Известно, что плотность, теплоёмкость и коэффициент температуропроводности
стекла составляют соответственно = 2500 кг/м3, ср = 0,67 кДж/(кг∙К) и а =
=4,42∙10−7 м2/с.
Решение
Коэффициенты теплопроводности и температуропроводности связаны между
собой следующим соотношением:
a
c p
или
ac p
Плотность теплового потока через стекло можно найти из закона Фурье:
t1c t 2c
q
t1c t 2c
q ac p
Подставим числовые значения:
1 ( 1)
q 4,42 10 670 2500
493,6 Вт/м2
0,003
7

21.

Задача 16. В теплообменнике горячий и холодный теплоносители разделены
плоской латунной стенкой [ = 2 мм, = 100 Вт/(м∙К)], перепад температур в
которой tс1 − tс2 = 5°С. Вычислить плотность теплового потока через стенку.
Определить толщину стальной [ = 45 Вт/(м∙К)] и медной [ = 370 Вт/(м∙К)]
стенок, чтобы при том же перепаде температур плотность теплового потока
осталась неизменной.
250 кВт/м2
0,9 мм
7,4 мм

22.

Задача 17. Плотность теплового потока через плоскую стенку толщиной 200 мм
составляет 200 Вт/м2, а разность температур её поверхностей 50°С. Определить
коэффициент температуропроводности стенки, если = 1700 кг/м3, ср = 0,88
кДж/(кг∙К).
5,35∙10−7 м2/с

23.

Задача 18. К двум торцам нагревателя цилиндрической формы d = 300 мм плотно
прижаты два идеальных образца материала того же диаметра толщиной = 5 мм.
Определить коэффициент теплопроводности образцов, если при мощности
нагревателя Q = 56,5 Вт перепады температур по толщине образцов составили
12,5°С. Радиальный перенос тепла в системе пренебрежимо мал (см. рис.).
Решение
Тепловой поток через образцы равна:
tc1 tc 2
Q
2F
tc 1 tc 2 t
d 2
F
4
Выразим коэффициент теплопроводности
Q
4Q
2Q
2
2
2F (t c 1 t c 2 ) 2 d t d t
Подставим числовые значения
2 56,5 0, 005
0,16 Вт/(м К)
2
3,14 0,3 12,5

24.

Задача 19. Обмуровка печи состоит из слоёв шамотного кирпича [ ш = 120 мм,
ш= 0,93 Вт/(м∙К)] и красного кирпича [ к = 250 мм, к = 0,70 Вт/(м∙К)], между
которыми засыпка из диатомита [ д = 60 мм, д = 0,13 Вт/(м∙К)]. Какой толщины
следует сделать слой засыпки, если толщину слоя из красного кирпича удвоить
при условии сохранения плотности теплового потока через обмуровку и
температур на внешних её поверхностях?
13,57 мм

25.

Задача 20. Окно в аудитории имеет сдвоенные рамы с зазором между стёклами 60
мм [ с = 0,74 Вт/(м∙К), в = 0,024 Вт/(м∙К)]. Вычислить тепловые потери через
оконный проём 3×3 м без учёта конвекции в зазоре и теплового излучения, если
толщина стёкол = 4 мм, а температуры их соответствующих поверхностей tс1 =
=12°С и tс4 = −15°С.
96,78 Вт

26.

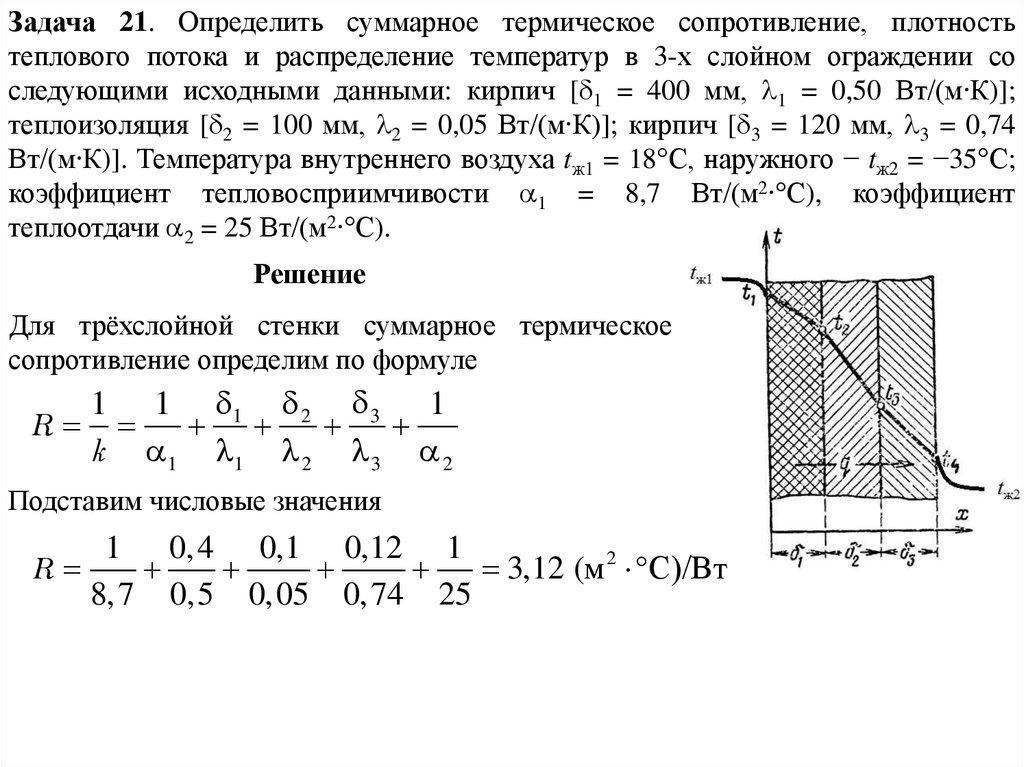
Задача 21. Определить суммарное термическое сопротивление, плотность
теплового потока и распределение температур в 3-х слойном ограждении со
следующими исходными данными: кирпич [ 1 = 400 мм, 1 = 0,50 Вт/(м∙К)];
теплоизоляция [ 2 = 100 мм, 2 = 0,05 Вт/(м∙К)]; кирпич [ 3 = 120 мм, 3 = 0,74
Вт/(м∙К)]. Температура внутреннего воздуха tж1 = 18°С, наружного − tж2 = −35°С;
коэффициент тепловосприимчивости 1 = 8,7 Вт/(м2∙°С), коэффициент
теплоотдачи 2 = 25 Вт/(м2∙°С).
Решение
Для трёхслойной стенки суммарное термическое
сопротивление определим по формуле
1 1 1 2 3 1
R
k 1 1 2 3 2
Подставим числовые значения
1 0, 4 0,1 0,12 1
R
3,12 (м 2 С)/Вт
8, 7 0,5 0, 05 0, 74 25

27.

Плотность теплового потока определим по выражению
q
t ж1 t ж2
t t
ж1 ж2
1 1 2 3 1
R
1 1 2 3 2
Определим числовое значение плотности теплового потока
q
18 ( 35)
17, 0 Вт/м 2
3,12
Распределение температур в многослойном ограждении определяется следующим
образом
q
t1 t ж1
1
1 1 2
t 3 t ж1 q
1 1 2
1 1
t 2 t ж1 q
1 1
q
t 4 t ж2
2

28.

Подставим числовые значения
t1 18
17
16, 0 С
8, 7
1 0, 4
t 2 18 17
2, 4 С
8, 7 0,5
1 0, 4 0,1
t 3 18 17
31, 6 С
8, 7 0,5 0, 05
17
t 4 35
34,3 С
25

29.

Задача 22. Определить общее термическое сопротивление, линейную плотность
теплового потока и распределение температур в 2-х слойном цилиндрическом
ограждении со следующими исходными данными: стальная труба с внутренним
диаметром d1 = 120 мм [ 1 = 3 мм, 1 = 54 Вт/(м∙К)]; теплоизоляция [ 2 = 100 мм,
2 = 0,06 Вт/(м∙К)]. Температура среды внутри трубы tж1 = 150°С, температура
наружного воздуха tж2 = −30°С; коэффициент тепловосприимчивости 1 = 550
Вт/(м2∙°С), коэффициент теплоотдачи 2 = 25 Вт/(м2∙°С).
Решение
Для двухслойной цилиндрической стенки суммарное
термическое сопротивление определим по формуле
d2 1
d3
1
1
1
Rl
ln
ln
1d1 2 1 d1 2 2 d 2 2d 3
Внешние диаметры трубы и изоляции найдём по выражениям
d 2 d1 2 1
d 3 d 2 2 2
Вычислим диаметры
d 2 120 2 3 126 мм
d 3 126 2 100 326 мм

30.

Подставим числовые значения в формулу для термического сопротивления
1
1
0,126
1
0,326
1
Rl
ln
ln
550 0,12 2 54 0,12 2 0, 06 0,126 25 0,326
8, 06 (м С)/Вт
Линейную плотность теплового потока определим по выражению
(t ж1 t ж2 )
ql
Rl
Определим числовое значение этой величины
3,14 (150 ( 30))
ql
70,1 Вт/м
8, 06
Распределение температур на границах слоёв определим по формулам
ql
t с1 t ж1
1d1
ql
t с3 t ж2
2d 3
d2
ql 1
1
t с2 t ж1
ln
1d1 2 1 d1

31.

Подставим числовые значения
70,1
149,7 С
t с1 150
3,14 550 0,12
70,1
1
1
0,126
t с2 150
ln
149, 7 С
3,14 550 0,12 2 54 0,12
70,1
t с3 30
27,3 С
3,14 25 0,326