Похожие презентации:
Тепловое излучение. Задачи
1.
Задание 1. Определить радиационный тепловой поток, испускаемый впространство верхней поверхностью горизонтальной квадратной плоской
пластины размерами 2x2 м с температурой T = 450 K и cтепенью черноты тела ε=
0,65.
Решение
Находим радиационный тепловой поток от абсолютно черного тела с
температурой 450 K:
Q 0 T 4 F
Определим действительный радиационный тепловой поток от тела со cтепенью
черноты тела ε = 0,65:
Q T 4 F
Подставим числовые значения:
Q 0,65 5,67 10 8 4504 2 2 6045 Вт
2.
Задание 2. Как изменится радиационный тепловой поток, испускаемый впространство нагретой поверхностью, если ее температура увеличится в 2 раза?
Решение
Радиационный тепловой поток от тела с температурой T1:
Q1 T14 F
И соответственно от тела с температурой T2:
Q 2 T24 F
Найдём отношение радиационных тепловых потоков:
Q2
Q1
T24 F
T14 F
T2
T1
4
Подставим числовые значения:
4
Q 2 2T1
16
Q1 T1
3.
Задание 3. Определить степень черноты нагретой поверхности, если известно,что при равных тепловых потоках температура абсолютно черного тела такой же
площади на 20% меньше?
Решение
Находим радиационный тепловой поток от абсолютно черного тела с
температурой Tачт:
4
Q Tачт
F
Определим температуру абсолютно чёрного тела через температуру нагретой
поверхности T:
Tачт 0,8T
Так как тепловой поток реальной нагретой поверхности:
Q T 4 F
Отсюда определим степень черноты тела:
4
Tачт
F Tачт
4
T F T
4
Подставим числовые значения:
4
0,8T
0,410
T
4.
Задание 4. Определить температуру электрического излучателя t1, если его длинаl = 3 м и диаметр d = 0,5 мм. Степень черноты поверхности провода ε = 0,9.
Температура ограждающей арматуры t2 = 20°С. Потребляемая мощность
составляет 0,5 кВт. Учесть только радиационный тепловой поток.
Решение
Определим площадь поверхности провода:
F dl
По условию вся потребляемая мощность затрачивается на излучение:
Q qF (T14 T24 ) dl
Определим температуру t1:
Q
(T14 T24 )
dl
T14
Q
T24
dl
t1 4
Q
T24 273
dl
Подставим числовые значения:
500
4
t1 4
293
273 929 C
8
4
0,9 5,67 10 3,14 5 10 3
5.
Задание 5. Определить температуру электрической спирали t, если её длина l = 5см и диаметр d = 0,3 мм. Степень черноты поверхности спирали ε = 0,3. При
напряжении U = 220 В величина тока в цепи I = 0,3 A. Считать, что вся теплота
теряется в результате излучения.
t = 2740°С
6.
Задание 6. Определить истинную температуру тела, если показания пирометрасоставляют t0 = 1100°С (T0 = 1373К) при применении красного фильтра (λ = 0,7
мкм = 0,7∙10−6 м). Степень черноты тела при указанной длине волны ελ = 0,65.
Решение
Находим яркость тела:
E
En
E E0
c1 5
En
(e c 2 T 1)
E0
c1 5
c T
e 2 1
c1 3,74 10 16 Вт м 2
c 2 1,44 10 2 м К
Определим интенсивность (яркость) абсолютно черного тела:
E0
c1 5
E0n
(e c 2 T0 1)
Из условия En = E0n получим:
e
c 2 T
e c 2
1 e
T0
1
c 2 T0
e c2
T
1
e c2
T
1
e c2
T0
1
7.
c2c2
ln
T0 T
1 1
ln
T T0 c 2
t
1
273
1
ln
T0 c 2
1
t
273 1140 C
7
1
7 10
ln 0,65
2
1373 1,44 10
8.
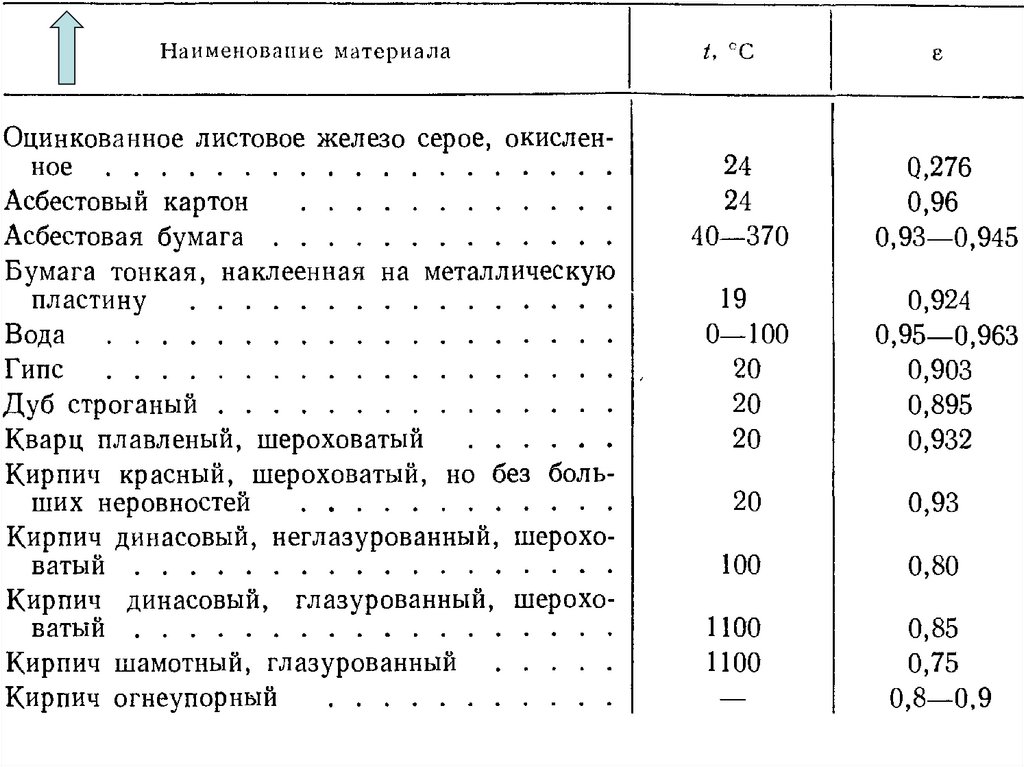
Задание 7. Определить потерю теплоты путём излучения с поверхности стальнойтрубы диаметром 70 мм и длиной 3 м при температуре поверхности 227 С, если
труба находится: а) в большом кирпичном помещении, температура стенок
которого 27 С; б) в кирпичном канале, площадь которого равна 0,3 0,3 м2 при
температуре стенок 27 С.
Решение
а) Согласно условию F1 << F2, поэтому εп = ε1.
По таблице для окиси стали определяем коэффициент черноты: 1 0,80
Тогда потери теплоты определим по формуле:
T1 4 T2 4
Q12 1c 0F1
100
100
F1 dl
Подставим числовые значения:
F1 3,14 0,07 3 0,66 м2
500 4 300 4
Q12 0,80 5,67 0,66
1630 Вт
100 100
9.
711
10.
11.
Определим площадь поверхности кирпичной стенки:F2 = 0,3 4 3 3,6 м2
Определим по таблице ε2 для кирпича: 2 0,93
Определим приведённый коэффициент черноты εп:
1
п
1 1 F1 F2 (1 2 1)
п
1
0,79
1 0,80 (0,66 3,6) (1 0,93 1)
Тогда потери теплоты определим по формуле:
T1 4 T2 4
Q12 пc 0 F1
100 100
500 4 300 4
Q12 0,79 5,67 0,66
1610 Вт
100 100
12.
13.
Задача 8. Определить средний угловой коэффициент и плотность тепловогопотока при теплообмене излучением между двумя бесконечными параллельными
пластинами. Расстояние между пластинами h = 4 м, ширина пластин a1= a2= 1,5 м.
Степень черноты пластин одинаковая ε1 = ε2 = 0,75. Температуры пластин t1 =
=450°С и t2 = 150°С.
Решение
Используя метод эффективных потоков, имеем:
Q12 Q л 12 E эф1 F1 21E эф2 F2
Учитывая, что:
1 Eс1
Eэф1 Eр1 1
A1 A1
Eэф2
1 Eс2
Eр2 1
A2 A2
Eс1 1 T14
Eс2 2 T24
Получим:
1
1 T14
1
2 T24
Q12 12 Eр1 1 F1 12
F1 21Eр2 1
F2
F2 21
A1
A2
A1
A2
14.
Учитывая, что для серого тела коэффициенты поглощения A1 = ε1 и A2 = ε2, атакже принимая во внимание выражения:
Q12 Eр1F12
Q 21 Eр2F21
Q12 Q 21
Получим:
1
1
4
Q12 12Q12 1 12 T1 F1 21Q12 1 21 T24F2
1
2
Преобразуя данное выражение, получим:
12 T14 F1 21 T24 F2
Q12
1
1
1 12 1 21 1
1
2
Учитывая, что 12F1 = 21F2, тогда для двух бесконечных параллельных пластин
одинаковой ширины согласно справочным данным табл.П.3.1 Приложения 3
средние угловые коэффициенты 12 = 21 равны:
2
h h
12 1
a a
2
4
4
12 1
0,181
1,5 1,5
15.
810
11
9
16.
Преобразуя данное выражение, получим:(T14 T24 ) 12
q12
1
1
1 12 1 21 1
1
2
Подставим числовые значения:
5, 67 10 8 (7234 4234 ) 0,181
q12
2210 Вт/м 2
1
1
1 0,181
1 0,181
1
0, 75
0, 75
17.
Задача 9. Определить тепловой поток при теплообмене излучением между двумядисками диаметрами d = 0,1 м. Расстояние между дисками h = 0,4 м. Степень
черноты дисков ε1 = ε2 = 0,8. Температуры дисков t1 = 400°С и t2 = 100°С.
Решение
Тепловой поток определим по выражению
12 T14 F1 21 T24 F2
Q12
1
1
1 12 1 21 1
1
2
Учитывая, что 12F1 = 21F2, тогда для двух бесконечных параллельных пластин
одинаковой ширины согласно справочным данным табл.П.3.1 Приложения 3
средние угловые коэффициенты 12 = 21 равны:
h
h
12 21 1
d
d
2
2
Подставим числовые значения:
2
2
0, 4
0, 4
12
1
0,015
0,1
0,1
18.
Преобразуя данное выражение, получим:(T14 T24 ) 12 F1
Q12
1
1
1 12 1 21 1
1
2
Q12
d 2
F1
4
(T14 T24 ) 12 d 2
1
1
4 1 12 1 21 1
1
2
Подставим числовые значения:
5, 67 10 8 (6734 3734 ) 0, 015 3,14 0,12
Q12
1, 23 Вт
1
1
4 1 0, 015
1 0, 015
1
0,8
0,8
19.
Задача 10. Определить средний угловой коэффициент излучения с меньшейпластины на большую при теплообмене излучением между двумя длинными
перпендикулярными пластинами (см. рис.).
Решение
Замкнем расчетную схему условными поверхностями 2 и 4.
Тогда средний угловой коэффициент для параллельных
поверхностей 1 и 2 согласно справочным данным табл.П.3.1
Приложения 3 найдем из выражения:
2
h h
12 1
a a
где h − расстояние между поверхностями 1 и 2 или ширина
поверхности 3, h = 2a; a − ширина поверхности 1.
Отсюда имеем
2
2a 2a
12 1
a
a
12 1 22 2 0, 236
Исходя из условий:
11 12 13 14 1
14 13
11 0
20.
Получим:2 13 1 12
13
1 12
2
13
1 0, 236
0,382
2
21.
Задача 11. Определить тепловой поток между двумя плоскими поверхностями,если между ними помещено два тонких экрана. Исходные данные: температуры
тел t1 = 300°С и t2 = 30°С; площади тел и экрана F1 = F2 = F = 5 м2; ширина тел и
экрана a1 = a2 = a = 1 м; расстояние между телами h = 0,4 м; степень черноты тел
ε1 = 0,8 и ε2 = 0,95; степень черноты экранов ε = 0,9.
Решение
Используя данные табл. П.3.1 Приложения 3, получим выражение для
определения теплового потока:
2
Q пр T T
4
1
4
2
F
12 1
h h
12 1
a a
Формулу для приведенной степени черноты определим по таблице П.3.2
пр
1
n
1 1
1
2 n 1
i 1 i
1
2
1
1 1 4
3
1 2
Подставим числовые значения:
2
0,4 0,4
12 1
0,677
1
1
пр
1
1
1
4
3
0,8 0,95 0,9
0,267
22.
Q 0,267 5,67 10 8 (5734 3034 ) 0,677 5 5090 Вт23.
Задача 12. Определить тепловой поток в результате теплообмена излучениеммежду поверхностями внутренних стен, пола и потолка с внутренней
поверхностью наружной стены. Исходные данные: размеры и высота помещения
соответственно axb = 4,4x5 м и h = 2,7 м; размеры наружной стены axh = 4,4x2,7
м; температура поверхности наружной стены tн = 14°С; температура воздуха в
помещении tв = 20°С; степень черноты всех поверхностей ε = 0,95; температура
поверхности внутренних стен при отсутствии теплообмена со смежными
помещениями tвн = 20°С.
Решение
Определяем суммарную площадь излучающих поверхностей:
F1 2ab (a 2b )h
Известно, что в замкнутых системах лучистого теплообмена, когда излучающая
поверхность (без самооблученных участков типа сферы) полностью окружена
облученными поверхностями, суммарная взаимная площадь излучения равна
площади меньшей из излучающей и облученной поверхностей. Так как
участвующие в лучистом теплообмене поверхности образуют замкнутую систему,
то суммарная взаимная площадь излучения равна:
F F2 ah
24.
Используя метод эффективных потоков, определим плотность результирующеготеплового потока:
Eр12
T14 T24
1 1
1
1 2
Используя метод эффективных потоков, определим результирующий тепловой
поток:
Q р12 Eр12 F2
Q р12
T1 Tвн
T2 Tн
1 2
Tвн4 Tн4
ah
2
1
Подставим числовые значения:
Q р12
5, 67 10 8 2934 2874
4, 4 2, 7 357 Вт
2
1
0,95
25.
Задача 13. Определить коэффициент ослабления луча слоем диоксида углеродатолщиной 40 мм, если после прохождения этого слоя интенсивность луча
уменьшилась на 80%.
Решение
Коэффициент ослабления луча в поглощающей среде αλ можно найти по закону
Бугера:
I , l I , l 0 e l
1 I ,l
Из этого закона выразим αλ: ln
l I ,l 0
По условию задачи:
I ,l
1 0,8
I ,l 0
Подставим числовые значения:
1
ln 1 0,8 40 м 1
0, 04
26.
Задача 14. Определить удельный тепловой поток излучением от дымовых газов кстенкам газохода при атмосферном давлении при следующих условиях: размеры
газохода 800x800 мм, температура стенки Tс = 350°С, степень черноты
поверхности εс = 0,95; газы имеют среднюю температуру Tг = 650°С, содержат
15% диоксида углерода и 6% водяных паров, парциальное давление которых
соответственно равно pCO2 = 15 кПа и p H2 O = 6 кПа.
Решение
Эффективную длину пути луча на 1 м длины газохода определим по
приближенному соотношению:
l m
4V
F
где V − объём газового тела; m = 0,9 − поправочный коэффициент; F − площадь
поверхности оболочки.
V 1 0,8 0,8 0,64 м3
4 0, 64
l 0,9
0,51 м
4, 48
F 4 1 0,8 2 0,8 0,8 4, 48 м2
27.
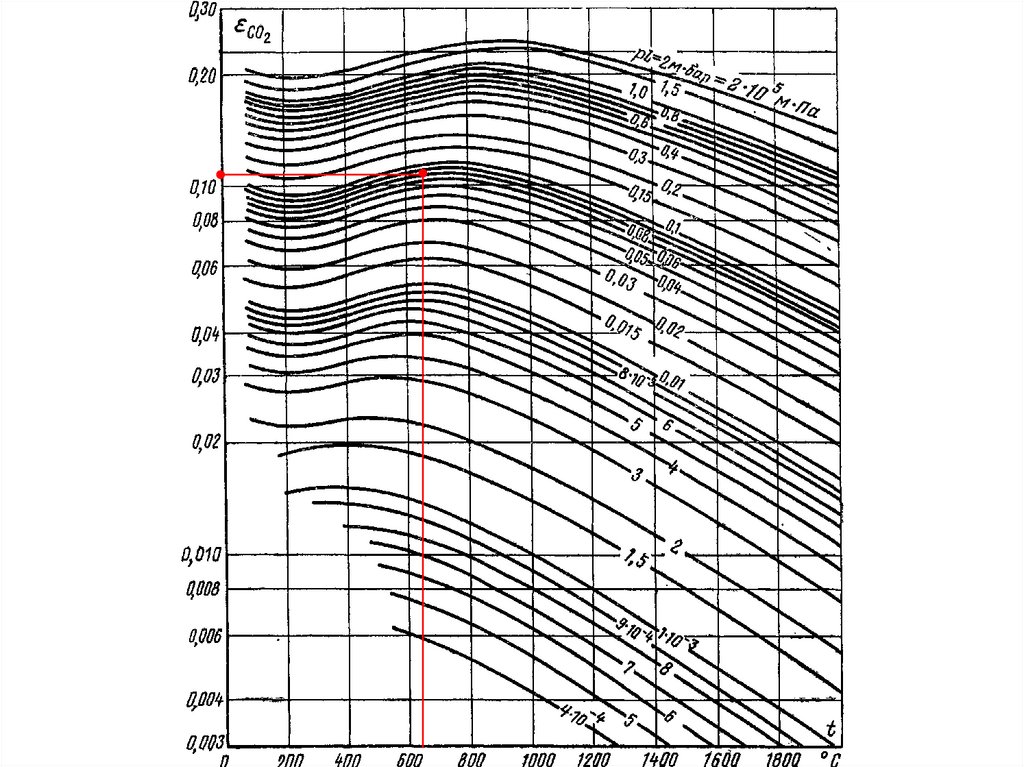
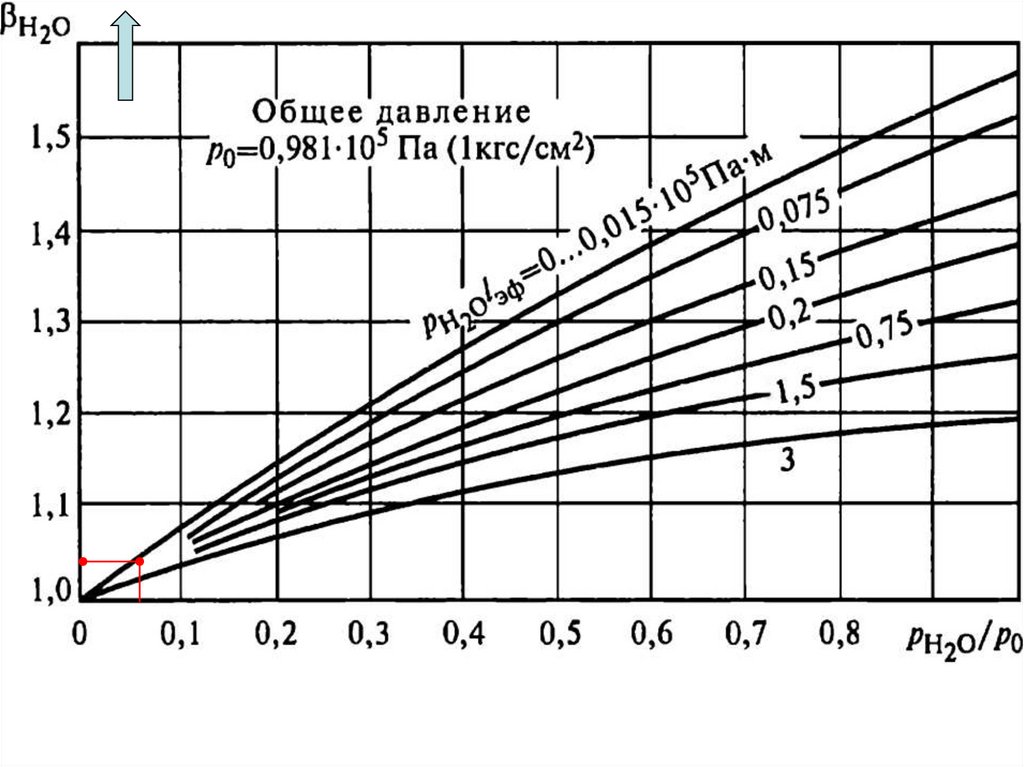
Определим произведения эффективной длины на парциальные давления:pCO2l 15000 0,51 7650 Па м 0,0765 105 Па м
pH2Ol 6000 0,51 3060 Па м 0,0306 105 Па м
По графикам определяем значения коэффициентов теплового излучения εCO2, εH2 O
и поправочного коэффициента β.
CO2 0,11
H 2O 0, 066
1, 04
Степень черноты дымовых газов определим по формуле:
г CO2 H 2O
г 0,11 1, 04 0, 066 0,179
Находим эффективный коэффициент черноты стенок канала:
с 0,5(1 с )
с 0,5 (1 0,95) 0,975
Отсюда удельный тепловой поток излучением от дымовых газов к стенкам
газохода при атмосферном давлении найдем по формуле:
ql с г (Tг4 Tс4 )
Подставим числовые значения:
q 0,975 0,179 5, 67 10 8 (9234 6234 ) 5690 Вт/м 2
28.
29.
30.
31.
Задача 15. Известно, что спектр излучения Солнца близок к спектру излученияабсолютно чёрного тела. Найти температуру поверхности Солнца, если
максимальное значение спектральной плотности потока его излучения
приходится на длину волны max = 0,5 мкм. Найти также интегральную плотность
потока и интегральную интенсивность излучения Солнца.
Решение
Температуру поверхности Солнца определим из закона смещения Вина
max
b
T
T
b
max
2,9 10 3
Подставим числовые значения
T
5800 К
7
5 10
Интегральную плотность потока определим по закону Стефана-Больцмана
E0 T 4
E0 5, 67 10 8 58004 64, 2 106 Вт/м 2 64, 2 МВт/м 2
Интегральную интенсивность (яркость) излучения определим по формуле
E0
I0
64, 2
I0
20, 4 МВт/(м 2 ср)
3,14
32.
Задача 16. Для серого тела известно: Eпад = 62,5 кВт/м2, Eпогл = 46,9 кВт/м2, T ==1000 К. Найти Eсоб.
Решение
Собственную интегральную плотность потока серого тела определим по формуле
Eсоб T 4
Степень черноты серого тела определим из выражения
Eпогл Eпад
Eпогл
Eпад
Подставим это выражение в формулу собственной интегральной плотности
потока излучения
Eсоб
Eпогл
T 4
Eпад
Подставим числовые значения
Eсоб
46,9
5, 67 10 8 10004 42500 Вт/м 2 42,5 кВт/м 2
62,5
33.
Задача 17. Чему равно значение для серого тела, если T = 1350 К, а Eсоб = 150,7кВт/м2.
Решение
Собственную интегральную плотность потока серого тела определим по формуле
Eсоб T 4
Выразим коэффициент черноты серого тела
Eсоб
T 4
Подставим числовые значения
150700
0,80
8
4
5, 67 10 1350
34.
Задача 18. Чему равны степень черноты серого тела и значение Eсоб притемпературе T = 800 К, если Eпад = 60 кВт/м2, Eпогл = 48 кВт/м2?
Решение
Степень черноты серого тела определим по формуле
Eпогл
Eпад
Подставим числовые значения
48
0,80
60
Собственную интегральную плотность потока серого тела определим по формуле
Eсоб T 4
Eсоб 0,8 5, 67 10 8 8004 18600 Вт/м 2 18, 6 кВт/м 2






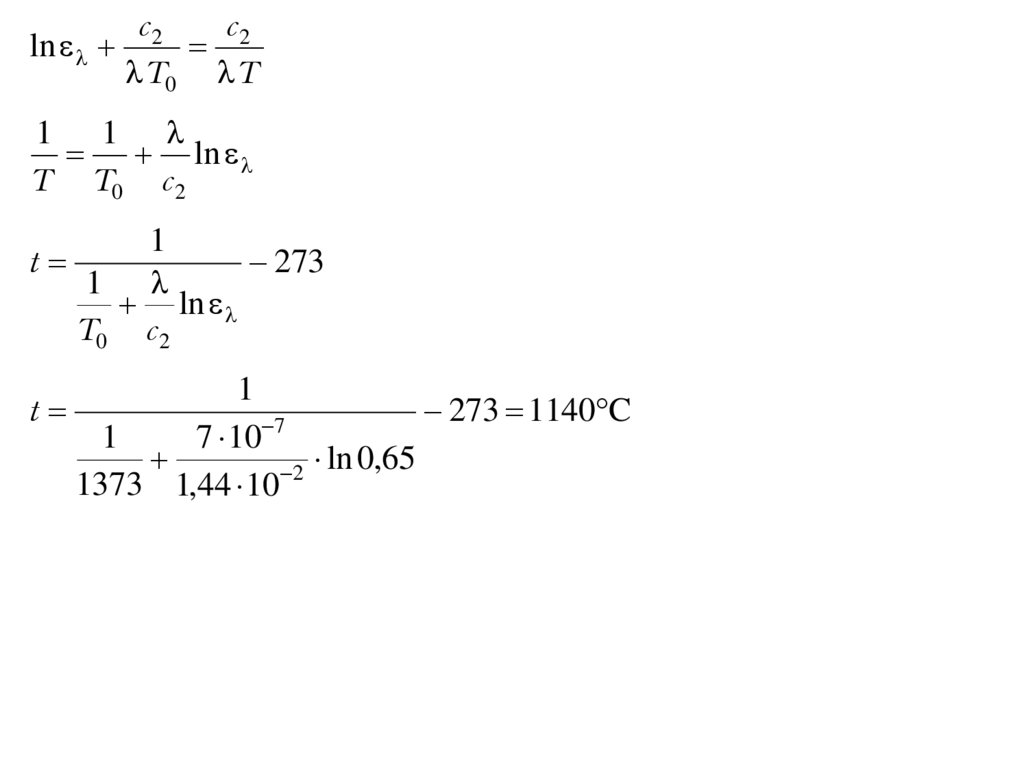
























 Физика
Физика








