Похожие презентации:
Линейная алгебра. Определители второго и третьего порядка. Определители n – ого порядка. Свойства определителей
1.
Линейная алгебраОпределители второго и третьего порядка.
Определители n – ого порядка.
Свойства определителей.
Методы вычисления определителей.
2.
Определители широко применяются во многихразделах высшей математики, в теоретической
механике, физике и т.д. для сокращения записей и
удобства вычислений.
Любой квадратной матрице порядка n можно
сопоставить
число,
которое
называется
определителем.
Обозначается det A или
A или .
Определитель матрицы также называется её
детерминантом.
Определитель
является
числовой
характеристикой квадратной матрицы.
3.
В общем случае перестановку записывают в видематрицы строки и обозначают малыми буквами
латинского алфавита.
Перестановку
1, 2, 3,
, n
называют нормальной.
4.
Определители n – ого порядкаОпределителем n – ого порядка называется число:
a11 a12
a 21 a 22
an1 an 2
a1n
a 2n
ann
5.
6.
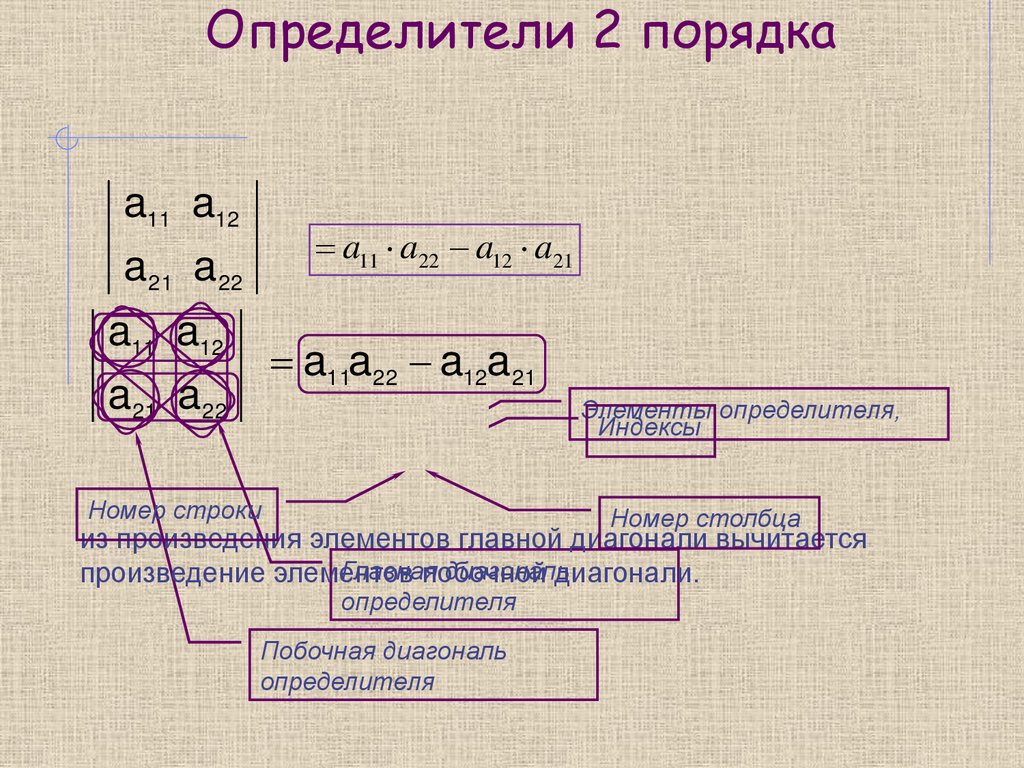
Определители 2 порядка7.
Определители 2 порядкаa11 a12
a11 a22 a12 a21
a 21 a22
a11 a12
a11a22 a12a21
a 21 a22
ai j
Номер строки
Элементы определителя,
Индексы
Номер столбца
из произведения элементов главной диагонали вычитается
Главная
диагональ
произведение элементов
побочной
диагонали.
определителя
Побочная диагональ
определителя
8.
Определители 3 порядка9.
Определители 3 порядкаОпределитель 3 - го порядка - это число, записанное в
виде:
a11a22a33 a12a23a31 a13a21a32 a13a22a31 a12a21a33 a11a23a32
Метод
треугольников
Французский
математик,
или схема Саррюса
профессор в
Страсбурге.
_
Работы его относятся к +
1различным
3 0 областям
2анализа
1 4 и 1 ( 1) 1 3 4 5 2 6 0 5 ( 1) 0
геометрии.
Пьер
Фредерик
Саррюс
5 6 1
29
1
6
4
2 3 1
(1798—1858)
Метод треугольника применим только для определителей 3 порядка
10.
Замечание:Определители 3-го порядка вычисляются с помощью
правила треугольников или путем приписывания
справа первых двух столбцов и тогда определитель
равен произведению элементов главной диагонали
минус произведение элементов побочной диагонали.
1
2
3 1 2
1 0 0 2 1 2 3 ( 8) 3
8 0 1 8 0 2 0 3 1 1 ( 3) 2 ( 8) 0
79
2 3 0 2 3
11.
Методы вычисления определителей1
Метод разложения определителя по элементам строки
(столбца) (основан на использовании теоремы Лапласа)
2
Метод элементарных преобразований или метод
приведения к треугольному виду (основан на
использовании свойств определителя)
3
Метод рекуррентных соотношений. (основан на
использовании предыдущих двух методов)
12.
Методы вычисления определителей1
Метод разложения определителя по элементам строки
(столбца)
Определитель (n-1)-ого порядка, который получается из
определителя n - ого порядка путем вычеркивания i - ой строки и
j - ого столбца, т.е. строки и столбца, на пересечении которых стоит
элемент ai j называется минором элемента и обозначается Mi j
Алгебраическим дополнением элемента ai j называется
Ai j ( 1)
aa1111 aa1212 aa1313
aa2121 aa2222 aa2323
aa3131 aa3232 aa3333
i j
Mi j
aa2211 aa2312
MM1123
aa3231 aa3332
2 3 1 1
( 1) M
23
M M 23
AA23 M
( 1)
11
11
11
13.
Методы вычисления определителейФранцузский
астроном,
Теорема Лапласа: Величина
определителя равна сумме
произведений
элементов
какой
– либо строки (столбца)
математик
и физик
Пьер
Симон
на их алгебраические
де определителя
Лаплас.
Научное
наследиедополнения:
n
Лапласа
к области
Разложение
определителя по элементам
относится
ai j A i j
ой строки
небеснойj 1 механики, i –математики
n
и
математической
физики,
Разложение
определителя по элементам
a
A
ij
ij
фундаментальными
являются
j – ого
столбца
i 1
работы
Лапласа
по
дифференциальным
уравнениям,
2 1 0
0 1
в частности по
интегрированию
0 3
3 1
1 2
1 3
1 1
0 3 1 2
1
(
1
)
0
(
1
)
(
1
)
методом «каскадов»
уравнений
2 с1
2 5
5
1
2
5
1
частными производными.
2 (3 1 5 1) 1 (0 1 2 1) 2
14.
Методы вычисления определителей2
Метод использования элементарных преобразований или
метод приведения к треугольному виду (основан на
использовании свойств определителя)
Свойства определителя:
Величина определителя:
равна нулю, если элементы какого - либо столбца или строки
равны нулю:
0 0
a21 a22
0 a22 0 a21 0
равна нулю, если соответствующие элементы двух строк
(столбцов) равны
a11 a12
a11 a12
a11 a12 a11 a12 0
15.
меняет знак, если поменять местами строки (столбцы):a11 a12
a21 a22
a11 a22 a12 a21 a12a21 a11a22
a12 a11
a22 a21
увеличивается в k раз, если элементы какого - либо столбца
(строки) увеличить в k раз:
k a11 k a12
a21
a22
k a11 a22 k a12 a21 k
a11 a12
a21 a22
не меняется при замене строк соответствующими столбцами:
a11 a12
a21 a22
a11 a21
a12 a22
16.
не меняется, если к элементам какой-либо строки (столбца)прибавить соответствующие элементы другой строки (столбца),
умноженные на произвольный множитель
a11
a12
a 21 ka11 a22 ka12
a11a 22 a 21a12
a11a 22 a11ka12 a21a12 ka11a12
a11 a12
a21 a22
Если определитель имеет так называемый треугольный вид,
то он вычисляется как произведение чисел, стоящих на
главной диагонали: a a a
11
12
13
0 a 22 a 23 a11a 22a 33
0 0 a 33
17.
Определителиданной
матрицы
транспонированной ей равны, т. е.
и
A A
T
«Фальшивое разложение определителя». Сумма
произведений элементов какой-либо строки
(столбца)
на
алгебраические
дополнения
соответствующих
элементов
другой
строки
(столбца) равна нулю.
Определитель произведения двух квадратных
матриц одного порядка равен произведению
определителей этих матриц, т.е.
A B A B
18.
Метод рекуррентных соотношений.3
1
3 1 ( 2)
2
1 3
+
1
+
1 4 1
3
1
0 5 1
0
7
2
1
5 1
7
2
( 1)1 1
5 2 7 1 17
Также, используя свойства, можно привести определитель к
треугольному виду и вычислить по последнему свойству.

















 Математика
Математика








