Обратная матрица. Матричные уравнения

1. Обратная матрица. Матричные уравнения

Раздел 1. Элементы линейной алгебры.
Тема 1.1.
Матрицы и определители.
Обратная матрица. Матричные
уравнения
Лекция № 7
ГБОУ СПО МО «ЛПТ»
Преподаватель математики
Осипова Людмила Евгеньевна
Mila139139 @ yandex.ru
УРОК СЕДЬМОЙ

2. Основное понятие

Квадратная матрица А = (аij ) , где i = j = 1,2,3,…,n,
называется невырожденной, если ее определитель
не равен нулю
Квадратная матрица А = (аij ) , где i = j = 1,2,3,…,n,
называется вырожденной, если ее определитель
равен нулю
На пример:
1 3
А=
- вырожденная матрица, т.к. det (А) = 9 - 9 = 0
3 9
2 7
В=
- невырожденная матрица, т.к. det (В) ≠ 0
0 1

3. Определение

Если квадратная матрица А невырожденная,
определитель, которой не равен нулю, то для нее
-1
существует обратная матрица А ,
которая задаётся условием:
-1
А А =А А =Е
где Е - единичная матрица

4. Введём понятие союзной матрицы

Матрица Α* называется союзной к квадратной
матрице Α , если элементы матрицы Α* равны
алгебраическим дополнениям
соответствующих элементов матрицы Α
Обратите внимание на индексацию алгебраических дополнений.
Α=
a11 a12 a13
a21 a22 a23
a31 a32 a33
A11 A21 A31
Α* = A12 A22 A32
A13 A23 A33
ВЫВОД
Таким образом, матрица имеет союзную тогда и только
тогда, когда она невырожденная.

5. Теорема

Всякая невырожденная матрица имеет обратную
Пусть задана матрица А ,
причём detA ≠ 0
Α=
a11 a12 a13
a21 a22 a23
a31 a32 a33
Доказательство
1) Таким образом, матрица A – невырожденная, т.к.
detА ≠ 0 , значит она имеет союзную A*
A11 A21 A31
Α* = A12 A22 A32
A13 A23 A33

6.

2) Найдём произведение матриц А и А*
А А* =
a11 a12 a13
a21 a22 a23
a31 a32 a33
A11 A21 A31
A12 A22 A32
A13 A23 A33
=
а11А11 + а12А12 + а13А13 ... а11А31 + а12А32 + а13А33
а21А11 + а22А12 + а23А13 ... а21А31 + а22А32 + а23А33
а31А11 + а32А12 + а33А13 ... а31А31 + а32А32 + а33А33
=
=
detA 0
0
0 detA 0
0
0 detA
т.е.
=
1 0 0
detA 0 1 0
0 0 1
А А* = detA E
=
= detA E ,
(1)

7.

3) Найдём произведение матриц А* и А
( аналогичным способом )
A* A =
=
A11 A21 A31
A12 A22 A32
A13 A23 A33
detA 0
0
0 detA 0
0
0 detA
т.е.
=
a11 a12 a13
a21 a22 a23
a31 a32 a33
1 0 0
detA 0 1 0
0 0 1
А* А = detA E
=
= detA E ,
(2)

8.

4) Сравнивая полученные результаты равенства (1) и (2)
с определением обратной матрицы, получаем
(1)
А*
А А* = detA E
А
= E
detA
(2)
-1
А =
А*
А* А = detA E
А
= E
detA
-1
А*
А =
1
=
detA
detА
Ч. Т. Д.
А*
A11 A21 A31
A12 A22 A32
A13 A23 A33
detA

9. Обратную матрицу вычисляют по формуле

А
где
1
-1
=
detА
A11 A21 A31 ….A n1
A12 A22 A32…. An2
…………………..
An1 An2 An3 …. Ann
detА – определитель матрицы А,
Аij – алгебраические дополнения для
элемента аij матрицы А.

10. Рассмотрим пример 1

3 2
Пусть дана матрица А = 6 4
Определить, существует ли обратная матрица А
-1
Решение.
3 2
А= 6 4
3 2
detA = 6 4
A – вырожденная матрица,
= 12 – 12 = 0
-1
следовательно, обратной для нее – A - не существует.
Ответ: нет

11. Рассмотрим пример 2

Пусть дана матрица А =
1 0 0
0 2 0
1 3 4
Определить, существует ли обратная матрица А
-1
Решение.
А=
1 0 0
0 2 0
1 3 4
detA =
1 0 0
0 2 0
1 3 4
= 1(8-0) + 1(0-0) = 8 ≠ 0
A – невырожденная матрица,
следовательно, обратная для нее существует и
находится по формуле:

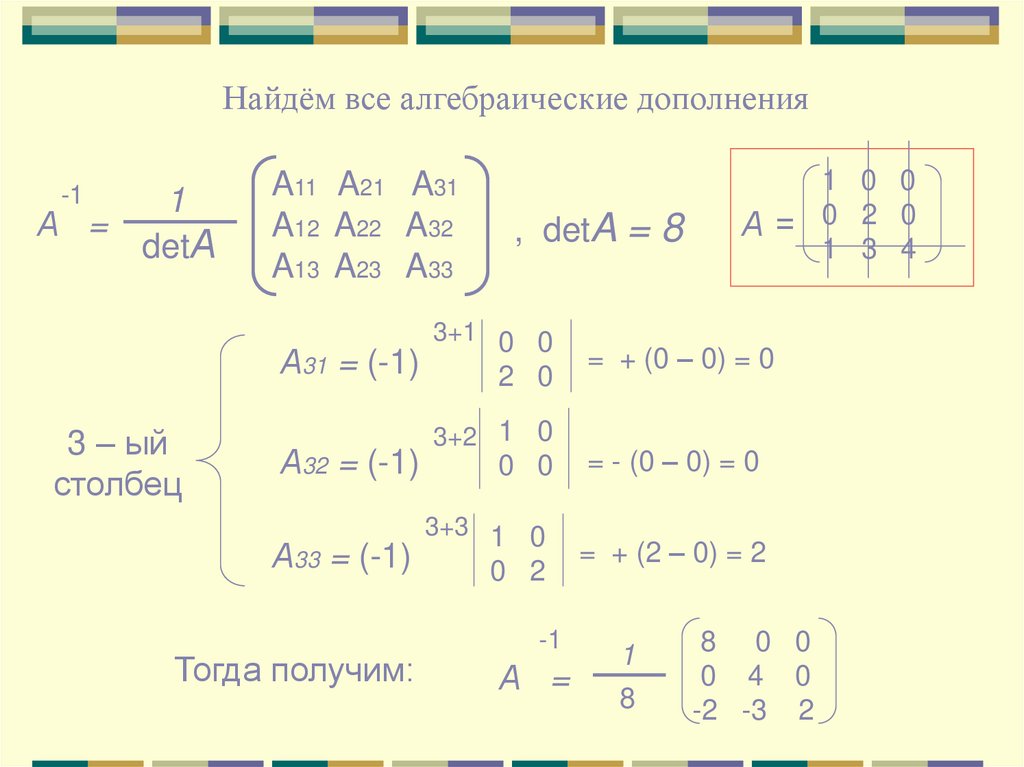
12. Найдём все алгебраические дополнения

-1
1
А =
detА
A11 A21 A31
A12 A22 A32
A13 A23 A33
А11 = (-1)
1 – ый
столбец
А12 = (-1)
, detA = 8
1+1 2 0
3 4
1+2 0 0
А13 = (-1)
1 4
1+3 0 2
1 3
1 0 0
А= 0 2 0
1 3 4
= + (8 – 0) = 8
= - (0 – 0) = 0
= + (0 – 2) = -2

13. Найдём все алгебраические дополнения

-1
1
А =
detА
A11 A21 A31
A12 A22 A32
A13 A23 A33
А21 = (-1)
2 – ой
столбец
А22 = (-1)
А23 = (-1)
, detA = 8
2+1 0 0
3 4
2+2
1 0
1 4
2+3 1 0
1 3
1 0 0
А= 0 2 0
1 3 4
= - (0 – 0) = 0
= + (4 – 0) = 4
= - (3 – 0) = -3

14. Найдём все алгебраические дополнения

-1
1
А =
detА
A11 A21 A31
A12 A22 A32
A13 A23 A33
А31 = (-1)
3 – ый
столбец
А32 = (-1)
А33 = (-1)
Тогда получим:
, detA = 8
3+1 0 0
2 0
3+2 1 0
0 0
3+3 1 0
0 2
-1
А =
1 0 0
А= 0 2 0
1 3 4
= + (0 – 0) = 0
= - (0 – 0) = 0
= + (2 – 0) = 2
1
8
8 0 0
0 4 0
-2 -3 2

15. Сделаем проверку

-1
А А =
=
1
8
8+0+0
0+0+0
-2+0+2
0+0+0
0+8+0
0-6+6
1
8
8 0 0
0 4 0
-2 -3 2
0+0+0
0+0+0
0+0+8
1
=
8
1 0 0
0 2 0
1 3 4
8 0 0
0 8 0
0 0 8
=
1 0 0
= 0 1 0
0 0 1
Значит, обратная матрица найдена верно
-1
Ответ:
А =
1
8
8 0 0
0 4 0
-2 -3 2
=Е

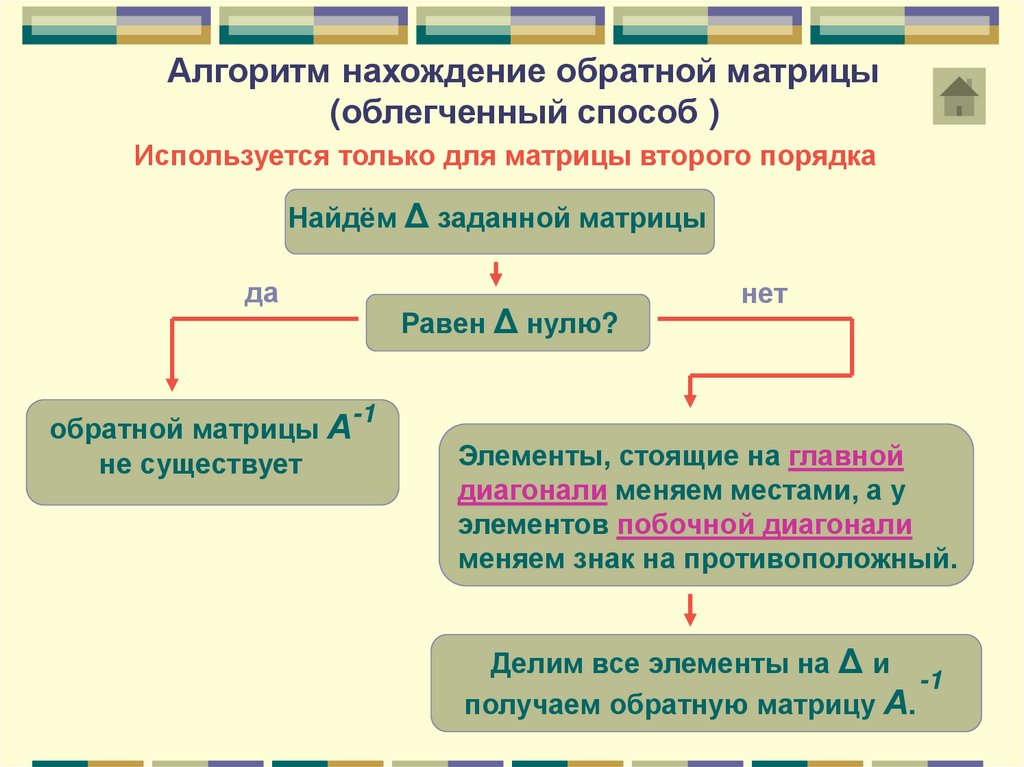
16.

Алгоритм нахождение обратной матрицы
(облегченный способ )
Используется только для матрицы второго порядка
Найдём Δ заданной матрицы
да
обратной матрицы Α
не существует
Равен Δ нулю?
нет
-1
Элементы, стоящие на главной
диагонали меняем местами, а у
элементов побочной диагонали
меняем знак на противоположный.
Делим все элементы на Δ и
-1
получаем обратную матрицу Α.

17. Рассмотрим пример 3

Задание.
-1
Найти обратную матрицу А для
1 1
1 2
А=
Решение.
1. Найдём определитель:
1 1
detA = 1 2
2. Соберём союзную матрицу:
2 -1
А* = -1 1
3. Разделим все элементы А* на Δ :
Ответ:
-1
А =
2 -1
-1 1
= 2 – 1 = 1≠ 0
-1
А =
2 -1
-1 1

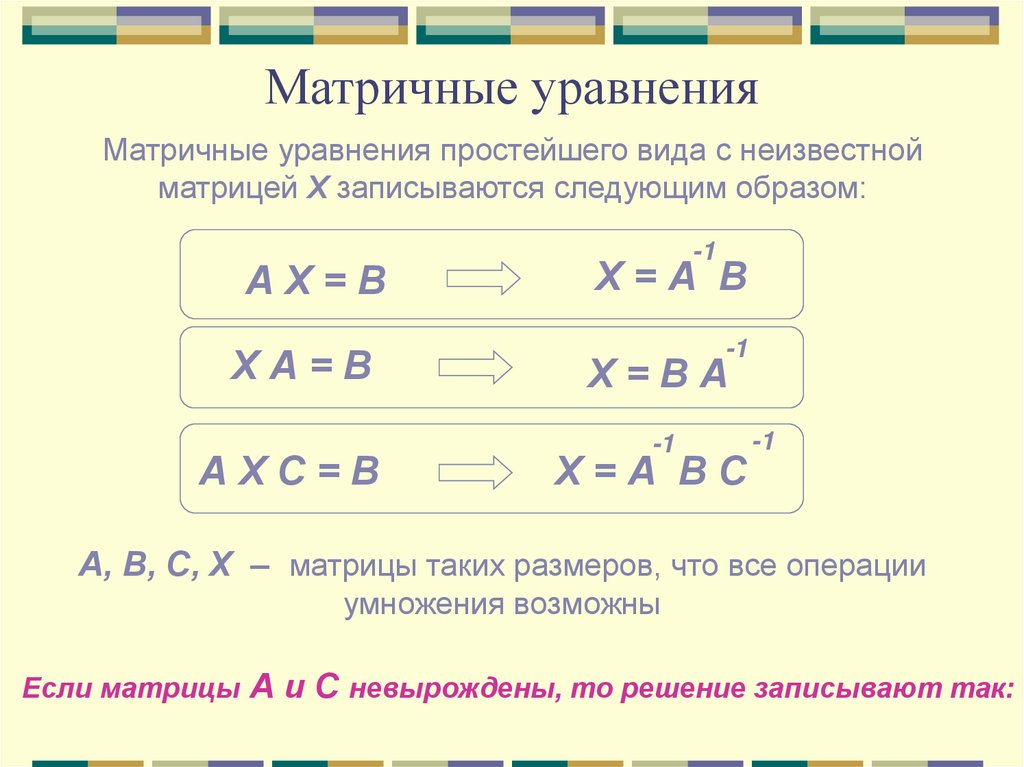
18. Матричные уравнения

Матричные уравнения простейшего вида с неизвестной
матрицей Х записываются следующим образом:
-1
АХ=В
Х=А В
ХА=В
-1
АХС=В
Х=ВА
-1
Х=А ВС
-1
А, В, С, Х – матрицы таких размеров, что все операции
умножения возможны
Если матрицы А и С невырождены, то решение записывают так:

19. Рассмотрим пример 4

Задание.
-3 0
5 -1
Решить матричное уравнение
-3 6
Х = 1 -4
Решение.
Запишем матричное уравнение в виде АХ = В
detA =
-3 0
5 -1
A =
-1
-1/3
Х=А В
= 3 ≠0
1 Α* = 1
3
Δ
-1
-1
0
Х = А В = -5/3 -1
-1 0
-5 -3
-3 6
1 -4
-1/3
0
= -5/3 -1
=
1 -2
6 -14
Ответ:
Х=
1
6
-2
-14

20. Решить самостоятельно

Найти обратную матрицу к матрице
Решение
ШАГ 1. Вычисляем определитель матрицы:
ШАГ 2. Вычислить алгебраические дополнения

21.

22.

ШАГ 3. Полученные значения подставим в исходную
формулу
Получим:
( ответ )

23. Основные источники

Лунгу К.Н. Сборник задач по высшей математике. 1 часть / К.Н.
Лунгу, Д.Т. Письменный, С. Н. Федин. – 7-е изд. – М.: Айрис –
пресс, 2008. - 576с.: ил. – ( Высшее образование )
Письменный Д.Т. Конспект лекций по высшей математике. 1
часть / Д.Т. Письменный – 5-е изд. – М.: Айрис – пресс, 2005.288с.: ил.
Тюрникова Г.В. Курс высшей математики для начинающих:
Учебное пособие. – М.: ГУ-ВШЭ, 2008. 376с.