Похожие презентации:
Определитель и его свойства. Обратная матрица
1. Определитель и его свойства
2.
Определение:Любой квадратной матрице n-го порядка
a11 a12 ..... a1n
А a21 a22 ..... a2 n
a
a
.....
a
n2
nn
n1
можно поставить в соответствие выражение,
которое называется определителем
(детерминантом) матрицы А, и обозначается
так:
a11
a12 .....
a1n
| A | = det A= ∆ = a
21
a22 .....
a2 n
an1
an 2 ..... ann
3.
1. Определитель второго порядка задаётсяравенством:
a11 a12
a21 a22
a11 a22 a12 a21
Пример 1:
2
4
0
5
2 5 0 4 10
4.
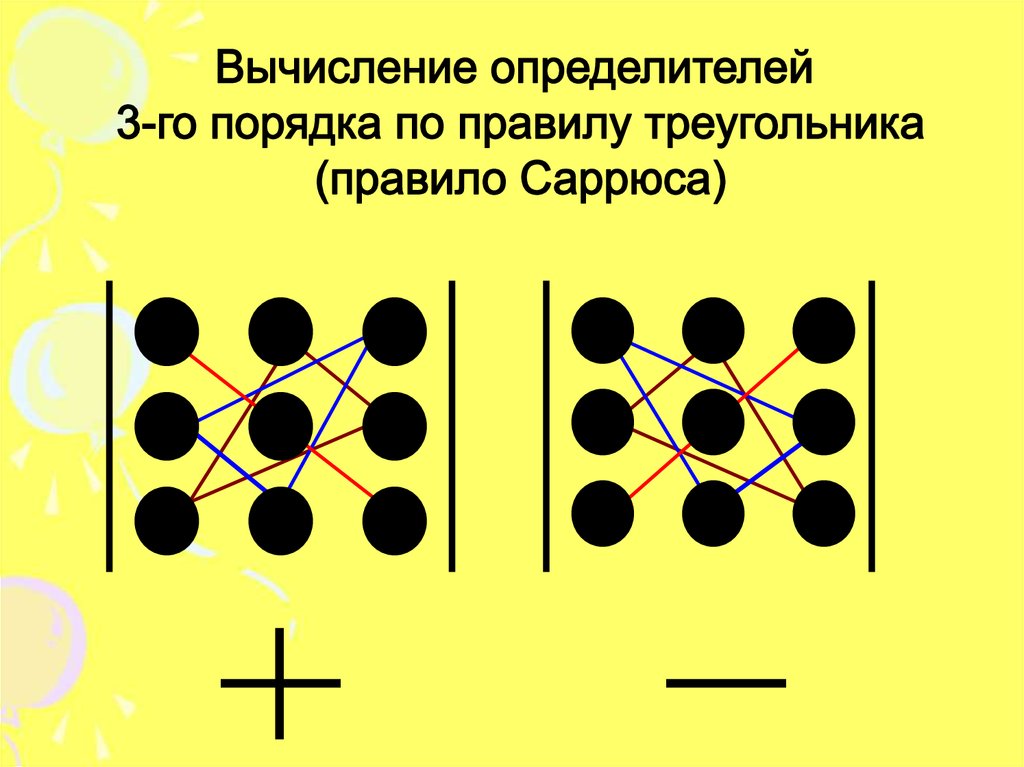
2. Определитель третьего порядка задаётсяравенством:
a11 a12 a13
a21 a22 a23 (a11 a22 a33 ) (a21 a32 a13 ) (a12 a23 a31 )
a31 a32 a33
(a13 a22 a31 ) (a21 a12 a33 ) (a23 a32 a11 )
Пример 2:
1
2
3
4
0
4 1 0 1 3 4 2 3 2 4
3 2 1
3 0 3 1 4 2 1 2 4 0
5.
6.
1. Если у определителя какая-либо строка (столбец)состоит только из нулей, то определитель равен нулю.
1
0
1 0 2 0 0
0
2
2. Если какие-либо две строки (два столбца)
определителя пропорциональны, то определитель
равен нулю.
1
1
1 3 3 1 3 3 0
3
3
7.
3. Если какую-либо строку (столбец) определителяумножить на любое число, то и весь определитель
умножиться на это число.
1 2
3
2
1
1 3
2
умножим на 2
первую строку
1
6 4 2
3
4
4. Если две строки (два столбца) определителя поменять
местами, то определитель изменит знак.
1
2
3
1
1 6 5;
2
1
6 1 5
3
1
8.
5. Если к какой-либо строке (столбцу) определителяприбавить, какую-либо другую строку (столбец)
умноженную на любое число, то определитель не
изменится.
1 3
2
3
1
1 2
Прибавим к первой строке
вторую, умножим на 2.
1 1 2 3 2 2
1
2
3 7
1 2
6 7 1
6. Определитель произведения матриц равен
произведению определителей.
А В
А В
9. Минор и алгебраическое дополнение
10.
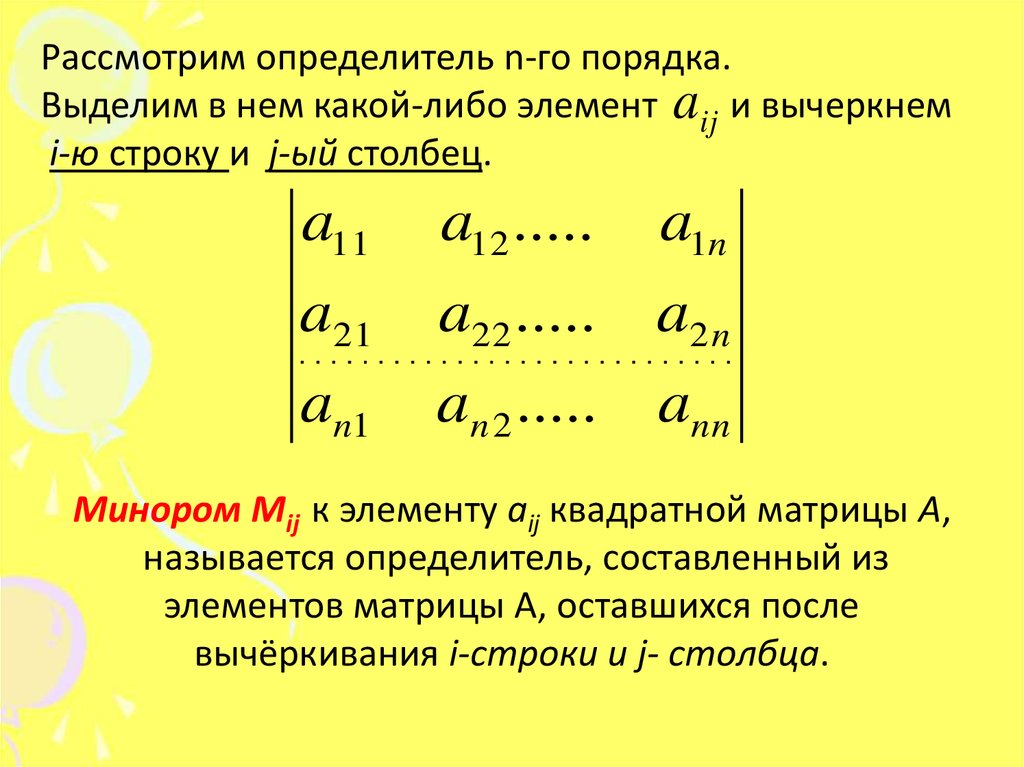
Рассмотрим определитель n-го порядка.Выделим в нем какой-либо элемент aij и вычеркнем
i-ю строку и j-ый столбец.
a11
a12 .....
a1n
a21
a22 .....
a2 n
an1
an 2 ..... ann
Минором Mij к элементу aij квадратной матрицы А,
называется определитель, составленный из
элементов матрицы А, оставшихся после
вычёркивания i-строки и j- столбца.
11.
Пример 3:Вычислить миноры для всех элементов матриц:
1)
1 2
0 7
M 11 7 7, M 12 0 0,
M 21 2 2, M 22 1 1.
12.
2)1 2 3
4
0
4
3 2 1
M 11
M 13
0
4
2
1
4
0
3 2
M 22 8,
8, M 12
8, M 21
4
4
3
1
2
3
2
1
M 23 4, M 31 8,
M 32 16, M 33 8.
16,
4,
13.
Алгебраическим дополнением элементаназывается число
i j
ij
A 1
aij
M ij
Пример 4:
Найти алгебраические дополнения для всех элементов
матриц
1)
1 2
0 7
2)
1 2 3
4
0
4
3 2 1
14.
Решение (пример 4):1)
A11 1 M11 7,
1 1
A12 1 M12 0,
1 2
A21 1 M 21 2, A22 1 M 22 1.
2 2
2 1
2)
A11 1 M 11 8,
1 1
A12 1 M 12 16,
1 2
A13 8, A21 4,
A22 8,
A31 8, A32 16, A33 8.
A23 4,
15. Обратная матрица.
16.
• Квадратная матрица порядка n называетсяневырожденной, если её определитель не
равен нулю.
n det A
a11
a12
... a1n
a 21
a 22
... a 2 n
...
...
...
a n1
an 2
... a nn
...
0
• В противном случае (detA=0) матрица А
называется вырожденной.
17.
• Если А- квадратная матрица, то обратнойпо отношению к матрице А называется
матрица, которая будучи умноженной на А
(как справа, так и слева) даёт
единичную матрицу.
1
1
A A A A E
18.
• Если обратная матрица существует, томатрица А называется обратимой.
• Операция
вычисления
обратной
матрицы при условии, что она
существует, называется обращением
матрицы.
19.
Теорема.Для того, чтобы квадратная матрица А
имела обратную, необходимо и достаточно,
чтобы матрица А была невырожденной
(detА≠ 0).
20. Нахождение обратной матрицы:
Aгде
A
T
A11
A12
...
A
1n
1
A
T
det A
An1
... An 2
... ...
... Ann
A21 ...
A22
...
A2 n
присоединенная матрица
21. Чтобы найти обратную матрицу:
1. находятdetA≠0;
detA
и
убеждаются,
что
2. находят
алгебраические
дополнения
всех элементов матрицы А и записывают
новую матрицу А*;
3. транспонируют новую матрицу
A
4. умножают полученную матрицу на
T
1
det A
;
22.
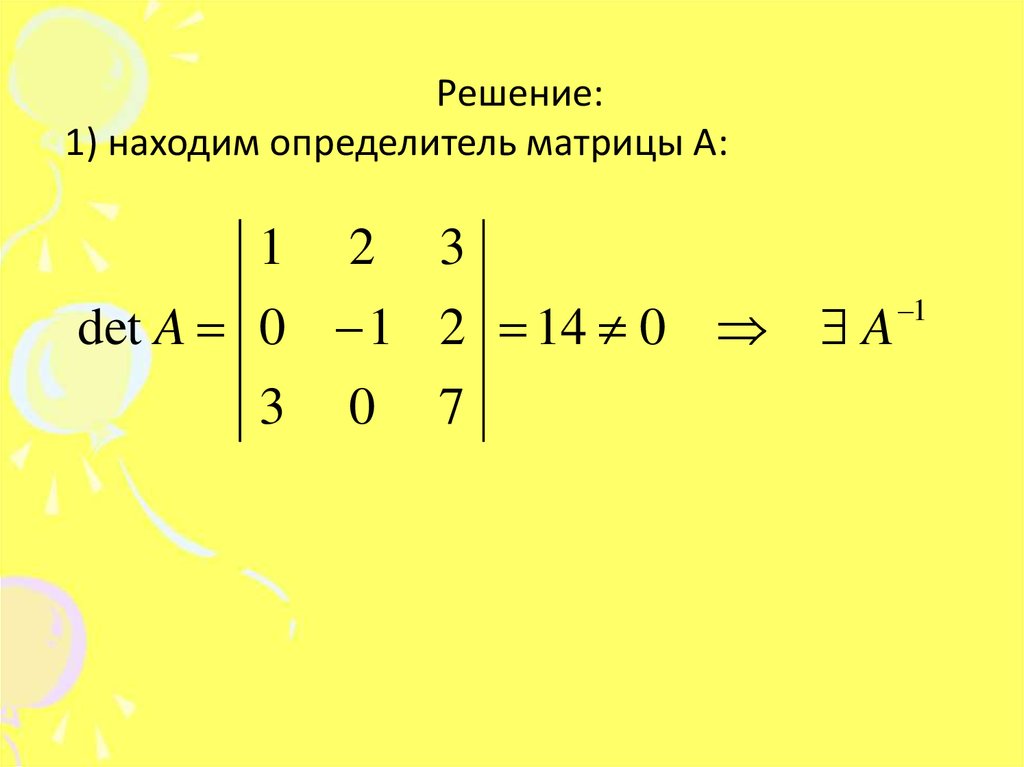
Пример 5.Найти матрицу, обратную к матрице А:
1 2 3
A 0 1 2
3 0 7
23. Решение: 1) находим определитель матрицы А:
12
3
det A 0 1 2 14 0 A
3
0
7
1
24. 2) находим алгебраические дополнения всех элементов матрицы А:
A11 11 2
A12 1
0 2
A13 1
0 1
2
0
3
4
7
3 7
3
7
0
6
3
A21 1
3
2 3
0 7
A22 1
1 3
A23 1
1 2
4
5
3 7
3 0
14
2
6
25.
A31 14
2
3
1 2
A32 1
1 3
A33 1
1
5
6
0 2
2
0 1
7
2
1
26. записываем новую матрицу:
63
7
записываем новую матрицу: A 14 2 6
7
2
1
3) транспонируем эту матрицу:
A
T
7 14 7
6
2 2
3
6
1
27. 4) умножим полученную матрицу на
1A
A
det A
1
7
14
6
14
3
14
1
2
14
6
14
T
1
det A
7 14 7
1
6
2 2
14
3
6
1
1
2
3
7
3
14
7
14
2
14
1
14
1
3
7
1
7
1
7
1
14
1
2
28. Проверка:
A 1 A A A 1 E7
1
2
3
14
6
1
A A 0 1 2 14
3 0 7 3
14
Ответ:
12
3
1
A 7
3
14
1
142
6
14
1
17
3
7
1 0 0
142 0 1 0
141 0 0 1
7
14
17
141
1
2





















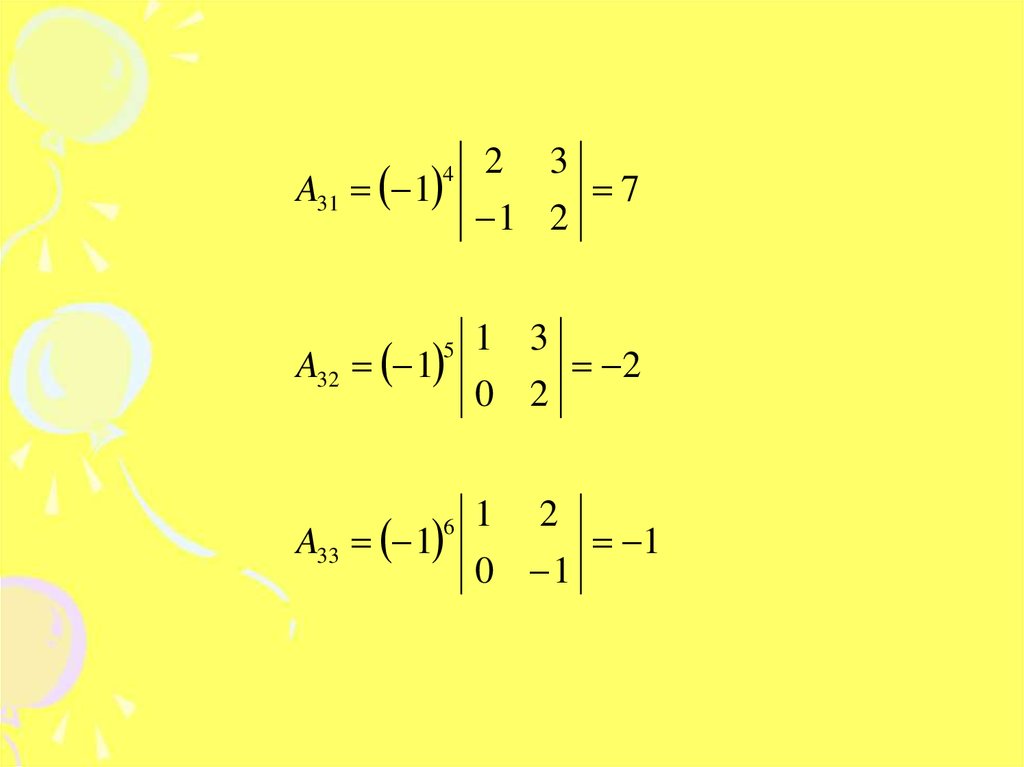



 Математика
Математика








