Похожие презентации:
Обратная матрица. (Тема 7)
1. Обратная матрица.
2.
• Квадратнаяматрица
порядка
n
называется невырожденной, если её
определитель не равен нулю.
n det A
a11
a12
... a1n
a 21
a22
... a2 n
...
an1
...
an 2
... ...
... a nn
0
• В противном случае (detA=0) матрица А
называется вырожденной.
3.
• Если А- квадратная матрица, то обратнойпо отношению к матрице А называется
матрица, которая будучи умноженной на
А (как справа, так и слева) даёт
единичную матрицу.
1
1
A A A A E
4.
• Если обратная матрица существует, томатрица А называется обратимой.
• Операция вычисления обратной матрицы
при условии, что она существует,
называется обращением матрицы.
5.
Теорема.Для того, чтобы квадратная матрица А
имела
обратную,
необходимо
и
достаточно, чтобы матрица А была
невырожденной (detА≠ 0).
6. Нахождение обратной матрицы:
1A
где
A
T
A11
A12
...
A
1n
A
T
det A
An1
... An 2
... ...
... Ann
A21 ...
A22
...
A2 n
присоединенная матрица
7. Чтобы найти обратную матрицу:
1. находятdetA≠0;
detA
и
убеждаются,
что
2. находят
алгебраические
дополнения
всех элементов матрицы А и записывают
новую матрицу А*;
3. транспонируют новую матрицу
A
4. умножают полученную матрицу на
T
1
det A
;
8.
Пример 1.Найти матрицу, обратную к матрице А:
1 2 3
A 0 1 2
3 0 7
9. 1) находим определитель матрицы А:
1 2 31
det A 0 1 2 14 0 A
3
0
7
10. 2) находим алгебраические дополнения всех элементов матрицы А:
1 27
0 7
A21 1
A12 1
0 2
6
3 7
A22 1
1 3
2
3 7
A13 1
0 1
3
3 0
A23 1
1 2
6
3 0
A11 1
2
3
4
3
4
5
2 3
14
0 7
11.
A31 14
2 3
7
1 2
A32 1
1 3
2
0 2
A33 1
1 2
1
0 1
5
6
12. записываем новую матрицу:
37 6
записываем новую матрицу: A 14 2 6
7 2 1
3) транспонируем эту матрицу:
A
T
7 14 7
6 2 2
3
6
1
13. 4) умножим полученную матрицу на
1A
A
det A
1
T
1
det A
7 14 7
1
6 2 2
14
3
6
1
147
6
14
3
14
1
142
6
14
12
3
7
143
7
14
2
14
1
14
1
17
3
7
17
141
1
2
14. Проверка:
A 1 A A A 1 E1 2 3 147 1 147 1 0 0
6
1
A A 0 1 2 14 142 142 0 1 0
3 0 7 3
0 0 1
6
1
14
14
14
Ответ:
12
3
1
A 7
3
14
1
17
3
7
17
141
1
2
15. Решение матричных уравнений.
A X B1
X A B
1
A
A X A B
E
1
E X A B
1
X A B
1
X
A
A B A
E
X E B A
X B A 1
1
1
16.
Пример 2.Найти матрицу Х:
A X C B
A X C B
1
1
1
A
A X C
C A B C
E
E
1
E X E A B C
1
X A B C
1
1
1
17.
Пример 3.Найти матрицу Х:
0
1 2 1
1
2 X 2 2
3 2
3 1 2
3 1
А
В
A X B
1
X A B
18.
1 21) det A 3 2
3
2)
1
2 1 0 A 1
1 2
2
2
A11
2
1 2
2 1
A21
3
1 2
3 2
A12
0
3 2
1 1
A22
1
3 2
3 2
A13
3
3 1
1 2
A23
5
3 1
19.
2 1A31
2
2
2
1 1
A32
1
3 2
1 2
A33
4
3 2
2 0 3
A 3 1 5
2 1 4
20.
3)4)
A
T
2 3 2
0
1
1
3 5 4
1
A
A
det A
1
T
2 3 2
0
1
1
3 5 4
21.
5)0 2 4
2 3 2 1
1
X A B 0
1
1 2 2 1 1
3 5 4 3 1 1 6
Проверка:
1 2 1 2 4 1 0
A X 3 2
2 1 1 2 2 B
3 1 2 1 6 3 1
22.
Ответ:2 4
X 1 1
1 6
23.
Пример 4. Показать, чтоAB
1
1
B A
1
24.
A BX CABX C
Пусть
AB X C
1
1
AB
AB
X AB C
E
X AB C
1
1
BX A C
1
1
1
B
B
X
B
A
C
X B 1 A 1 C
1
X C AB C
C
1
X C 1 B 1 A 1 C
C
E
XC AB
1
E
E
1
1
1
1
A
A
BX
A
C
1
Получили, что
E
XC 1 B 1 A 1
AB
1
B 1 A 1










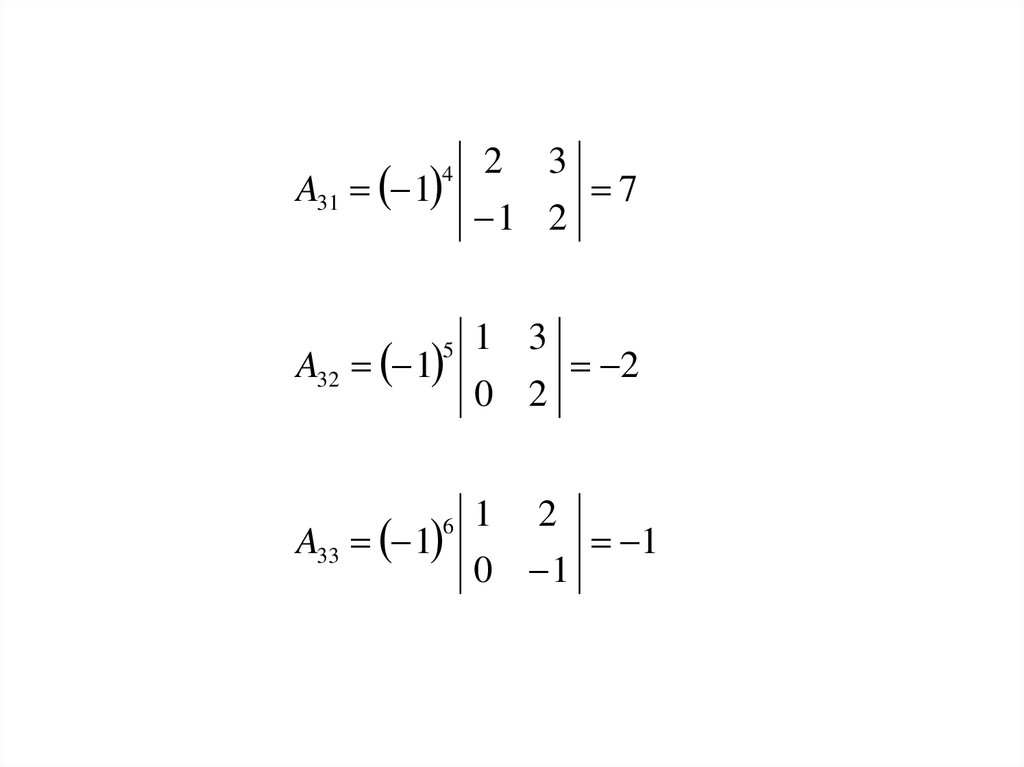






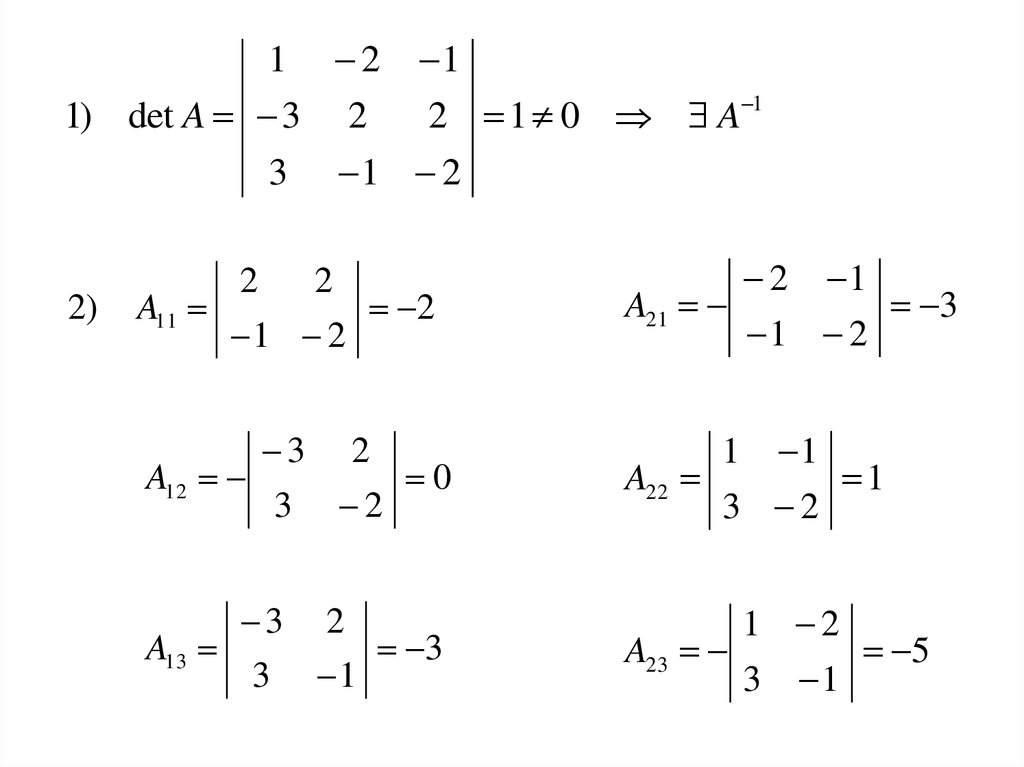


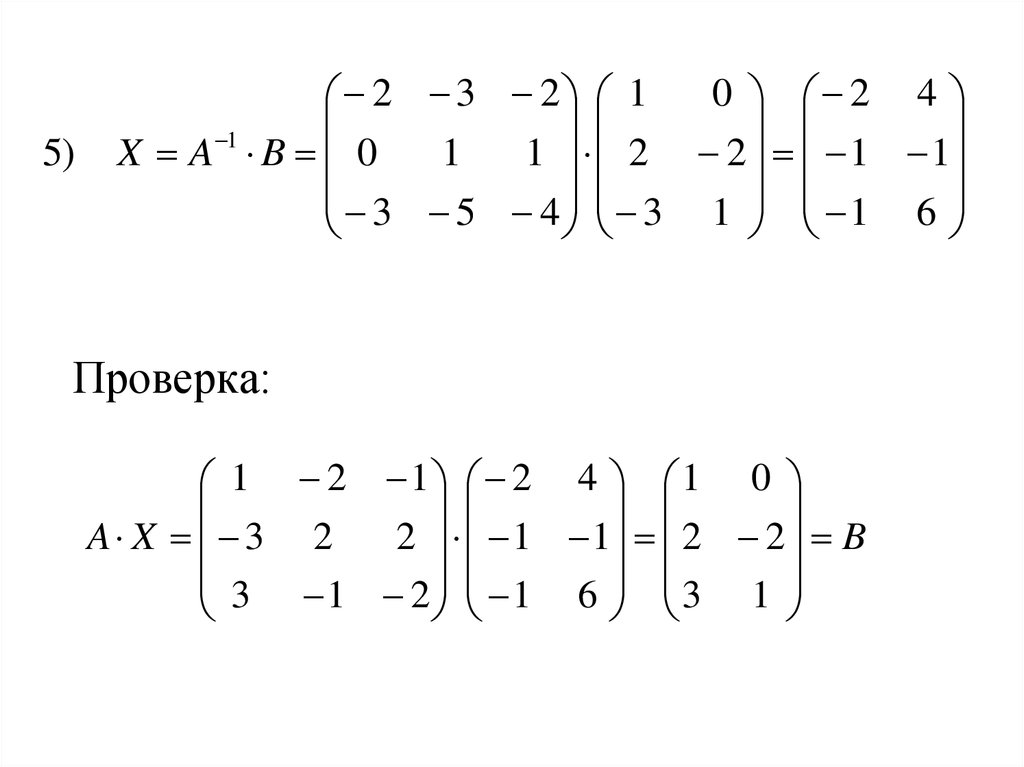



 Математика
Математика








