Гипербола. Понятие гиперболы

1.

Гипербола
КУРБАНОВ НУРИСЛАН

2.

Понятие гиперболы
Гиперболой называется множество всех таких
точек плоскости, для которых модуль разности
расстояний до двух фиксированных точек есть
постоянная положительная величина.
Фиксированные точки - фокусы гиперболы

3.

График гиперболы

4.

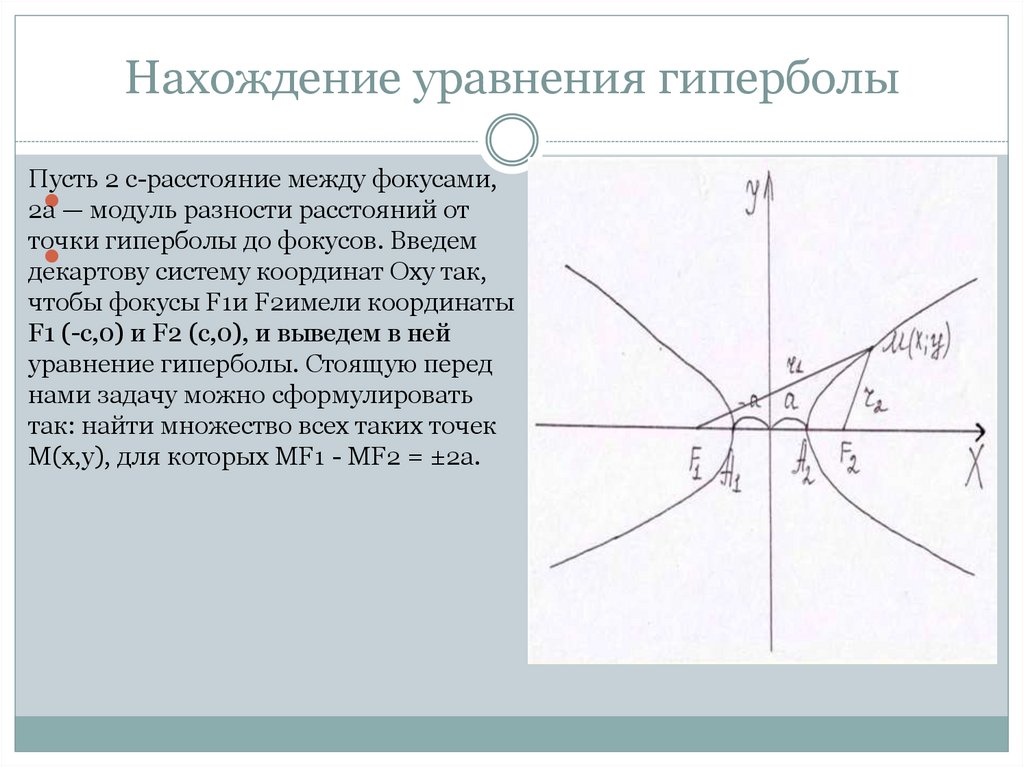
Нахождение уравнения гиперболы
Пусть 2 с-расстояние между фокусами,
— модуль разности расстояний от
2а
точки гиперболы до фокусов. Введем
декартову
систему координат Оху так,
чтобы фокусы F1и F2имели координаты
F1 (-с,0) и F2 (c,0), и выведем в ней
уравнение гиперболы. Стоящую перед
нами задачу можно сформулировать
так: найти множество всех таких точек
M(x,y), для которых MF1 - MF2 = ±2а.

5.

Нахождение уравнения гиперболы
Из неравенства треугольника следует, что |MF1 -
MF2| ≤ F1F2 т.е. a ≤ c. При а = с гипербола
вырождается в два луча прямой F1F2 поэтому
будем считать, что а < с. В координатах
уравнение гиперболы принимает вид:

6.

Каноническое уравнение гиперболы
Выполнив стандартные преобразования
получим:

7.

Свойства гиперболы
Гипербола имеет две взаимно перпендикулярные оси симметрии (оси Ох и
Оу), а значит, и центр симметрии (начало координат О). Оси симметрии
гиперболы называются ее полуосями: та из них, на которой лежат фокусы,
называется вещественной полуосью, а другая — мнимой; числа а и b
иногда также называют полуосями.
Поскольку
то в полосе (|х| <a), содержащей мнимую ось
гиперболы, точек гиперболы нет.
Поскольку
то в области между двумя пересекающимися
прямыми (|y| ≥ (b/a) |x|) точек гиперболы также нет.
Гипербола имеет асимптоты y=±(b/a) x.

8.

Вывод о гиперболе
Гипербола является множеством всех таких точек
плоскости, для которых отношение расстояния
до фиксированной точки (фокуса) к расстоянию
до фиксированной прямой (директрисы)
постоянно и больше единицы.
Любая прямая имеет с гиперболой не более двух
точек.