Приложения дифференциального исчисления

1. Приложения дифференциального исчисления

6. Исследование функций с
помощью производных

2. Схема исследования функции y=f(x)

1) Область определения D(f). Точки разрыва.
2) Чётность, периодичность.
3) Асимптоты графика функции. Поведение
на бесконечности.
4) Пересечение с осями координат.
5) Промежутки монотонности и точки
экстремума функции.
6) Промежутки выпуклости и точки перегиба
графика функции.

3. Схема исследования функции y=f(x)

1) Найти область определения D(f) функции.
Определить характер точек разрыва (найти
односторонние пределы в точках разрыва).
1
y
g ( x) 0
g ( x)
y log a g ( x) g ( x) 0
y arcsin g ( x)
y 2 n g ( x) g ( x ) 0
y arccos g ( x)
y tg ( g ( x)) g ( x)
1 g ( x) 1
n, n Z
2
y сtg ( g ( x)) g ( x) n, n Z

4. Схема исследования функции y=f(x)

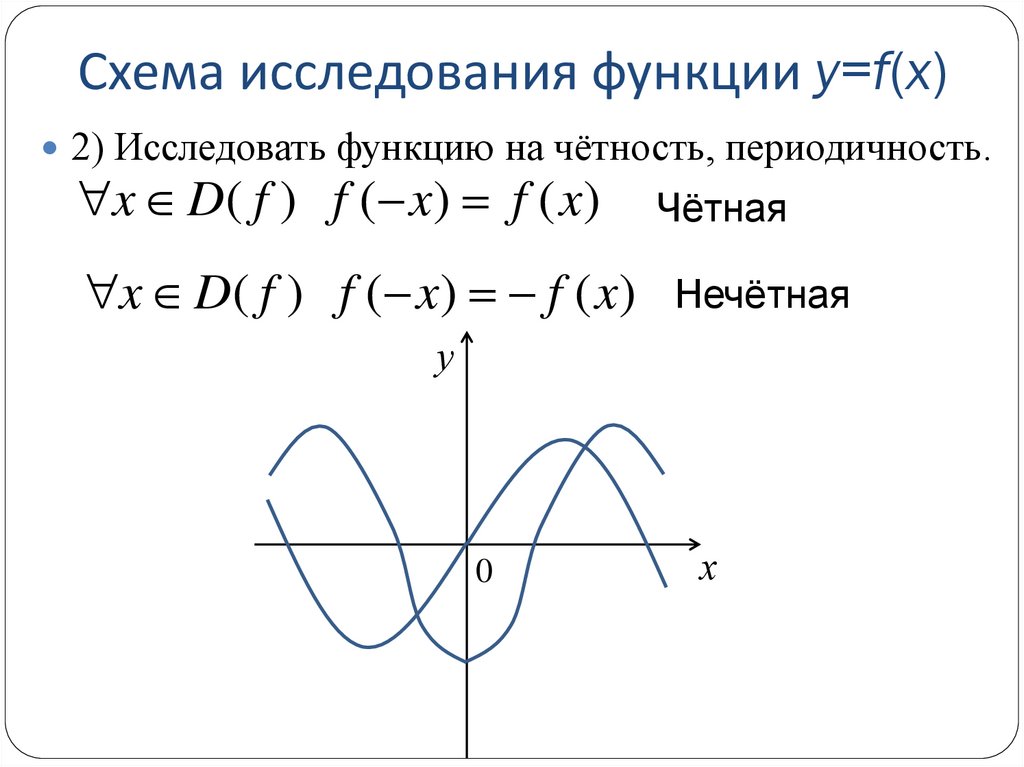
2) Исследовать функцию на чётность, периодичность.
x D( f ) f ( x) f ( x)
Чётная
x D( f ) f ( x) f ( x)
Нечётная
у
0
х

5. Схема исследования функции y=f(x)

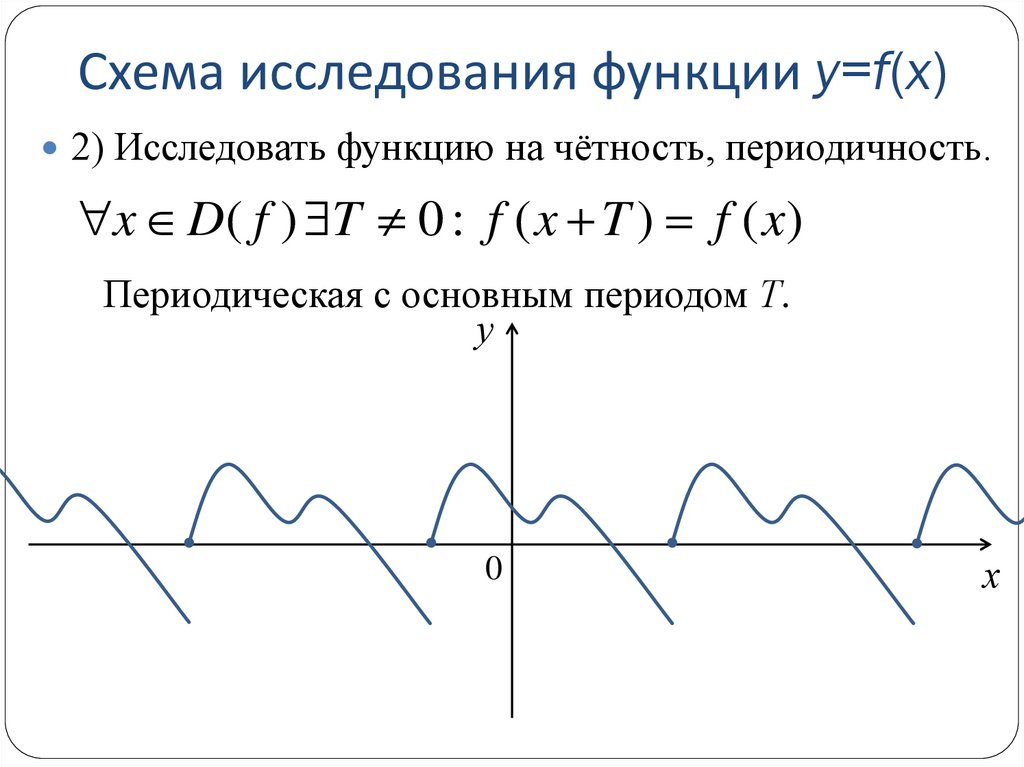
2) Исследовать функцию на чётность, периодичность.
x D( f ) T 0 : f ( x T ) f ( x)
Периодическая с основным периодом Т.
у
0
х

6. Схема исследования функции y=f(x)

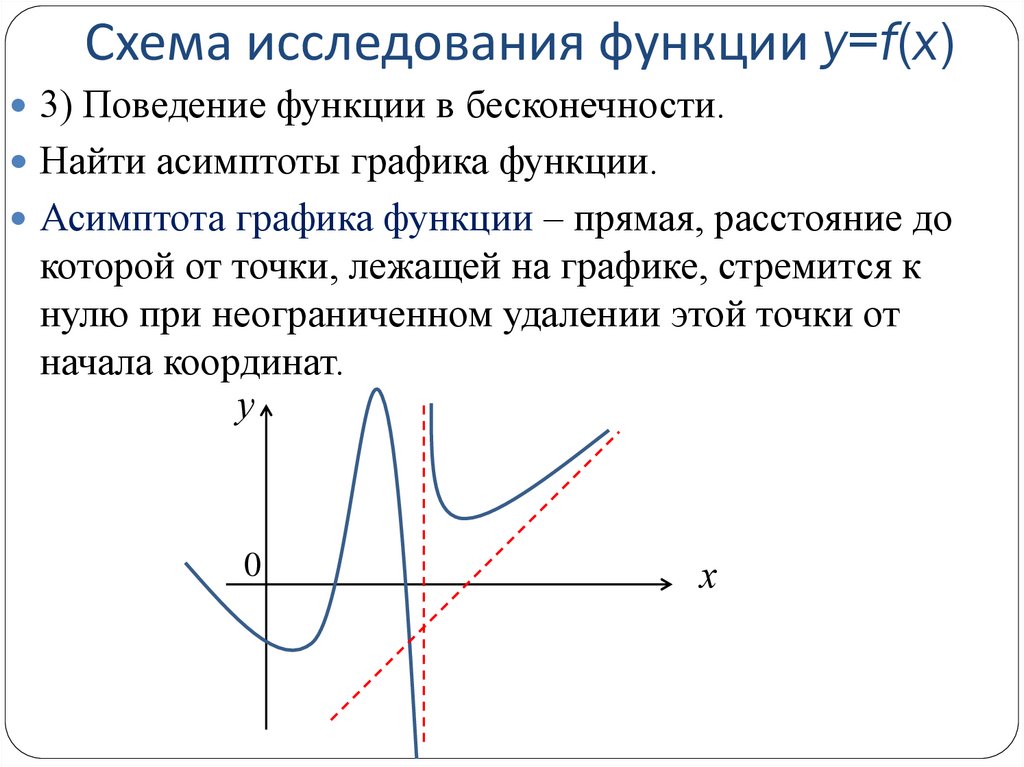
3) Поведение функции в бесконечности.
Найти асимптоты графика функции.
Асимптота графика функции – прямая, расстояние до
которой от точки, лежащей на графике, стремится к
нулю при неограниченном удалении этой точки от
начала координат.
у
0
х

7. Асимптоты

Вертикальные
Наклонные
Горизонтальные
x x0
y kx b
y b
lim f ( x)
f ( x)
k lim
x
x
k 0
x x0 0
lim f ( x)
x x0 0
х0 – точки
разрыва
второго рода
b lim ( f ( x) kx)
x
b lim f ( x)
x

8. Схема исследования функции y=f(x)

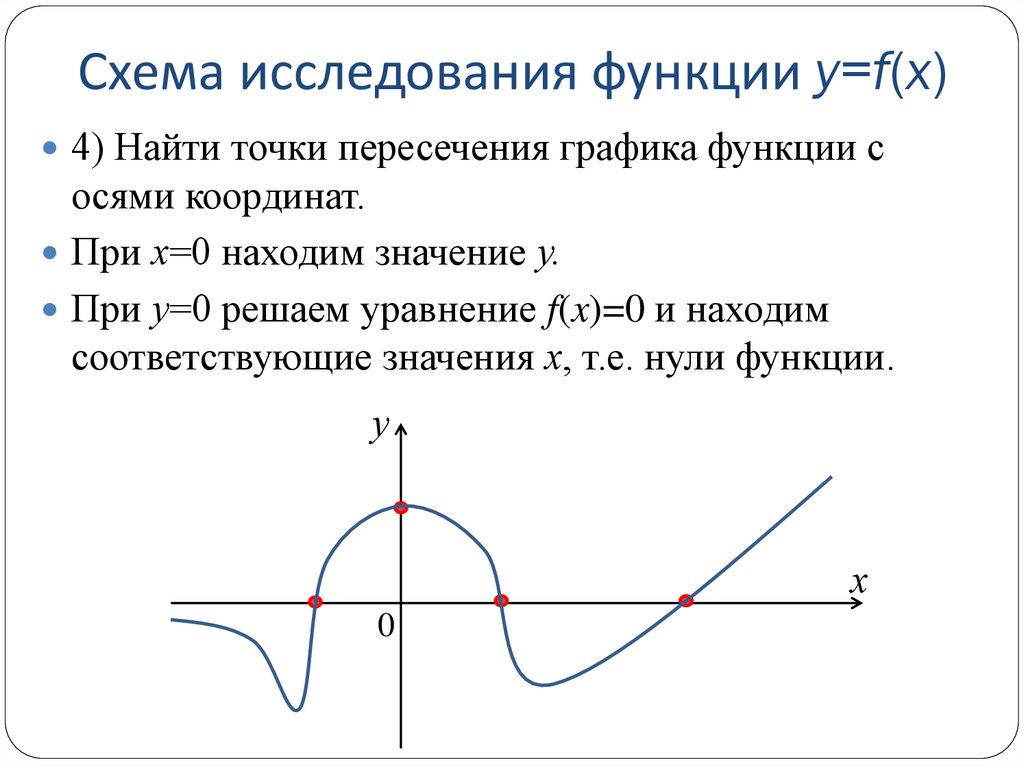
4) Найти точки пересечения графика функции с
осями координат.
При х=0 находим значение у.
При у=0 решаем уравнение f(x)=0 и находим
соответствующие значения х, т.е. нули функции.
у
х
0

9. Схема исследования функции y=f(x)

5) Найти промежутки монотонности и точки
экстремума функции.
6) Найти промежутки выпуклости и точки перегиба
графика функции.
На основе проведенного
исследования построить график
функции

10. Исследовать функцию и построить ее график

х
у
6 2х
1) Область определения D(f). Точки разрыва.
2) Чётность, периодичность.
3) Асимптоты графика функции. Поведение
на бесконечности.
4) Пересечение с осями координат.
5) Промежутки монотонности и точки
экстремума функции.
6) Промежутки выпуклости и точки перегиба
графика функции.
2

11. Исследовать функцию и построить ее график

х
у
6 2х
1) Область определения D(f). Точки разрыва.
D( f ) : 6 2 х 0
х 3
х2
lim
x 3 6 2 х
х
lim
x 3 6 2 х
2
2

12. Исследовать функцию и построить ее график

х
у
6 2х
2
2) Чётность, периодичность.
( х) 2
x2
f ( x)
6 2( х) 6 2 x
Функция общего вида

13. Исследовать функцию и построить ее график

х
у
6 2х
3) Асимптоты графика функции. Поведение на
бесконечности.
2
x 3 - вертикальная асимптота
f ( x)
х
1
k lim
k
lim
x
x
x 6 2 х
2
х2
1
b lim ( f ( x) kx) lim
x
x
x 6 2 х
2
6х
3
lim
x 6 2 х
2

14. Исследовать функцию и построить ее график

х
у
6 2х
3) Асимптоты графика функции.
x 3
x 3 - вертикальная асимптота y - наклонная асимптота
2 2
Поведение на бесконечности.
х2
lim
x 6 2 х
х
lim
x 6 2 х
2
2

15. Исследовать функцию и построить ее график

х
у
6 2х
4) Пересечение с осями координат.
2
x 0 y 0
х
y 0
0 х 0
6 2х
5) Промежутки монотонности
экстремума функции.
2
и
точки

16. Исследовать функцию и построить ее график

х
у
6 2х
5) Промежутки монотонности и точки
экстремума функции.
2
х 2 х (6 2 x ) 2 x 2 2 х (6 2 x ) 2 x 2
у
2
2
(6 2 х )
(6 2 х )
6 2х
12 х 2 x
2
(6 2 х )
12 х 2 x 2 0
2 х 0,
6 x 0;
х 0,
x 6
2
2 х (6 x ) 0
2

17. Исследовать функцию и построить ее график

х
у
6 2х
5) Промежутки монотонности и точки
экстремума функции.
2
2
х 12 х 2 x
х 0, у (0) 0
у
2
(6 2 х )
x 6
6 2х
62
у (6)
6
6
2
6
у
-
у
+
0
-
+
3
2
6

18. Исследовать функцию и построить ее график

х
у
6 2х
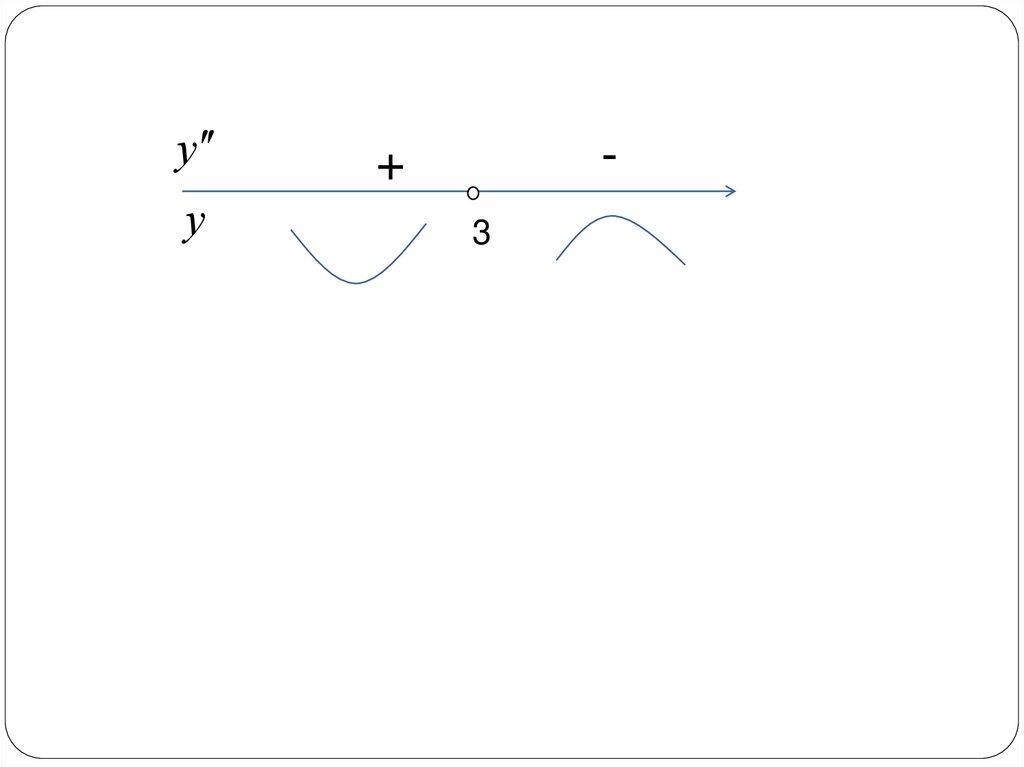
6) Промежутки выпуклости и точки перегиба
графика функции.
2
12 х 2 x
у
2
(6 2 х )
2
(12 4 x) (6 2 х) 4(12 x 2 x )(6 2 х)
4
(6 2 х )
2
2
(12 4 x) (6 2 х) 4(12 x 2 x )
72
3
3
(6 2 х )
(6 2 х )
2

19.

у
у
-
+
3

20.

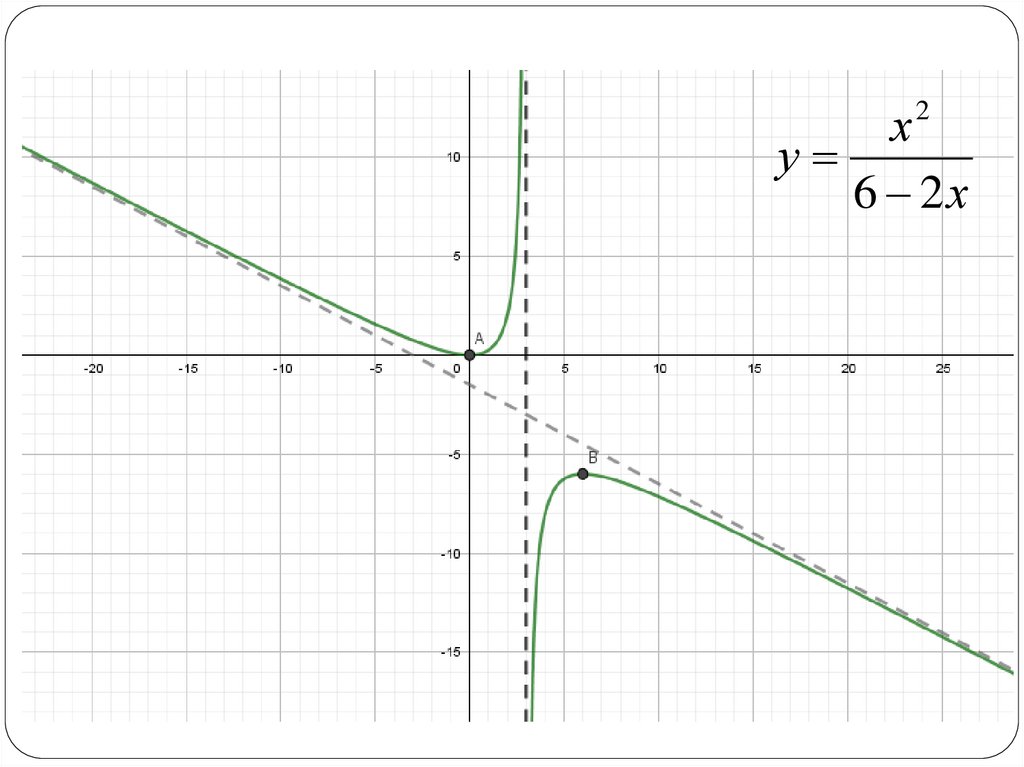
х2
у
6 2х