Цилиндр. Площадь боковой поверхности цилиндра

1.

ЦИЛИНДР
Свирцева Ольга 11 «а»

2.

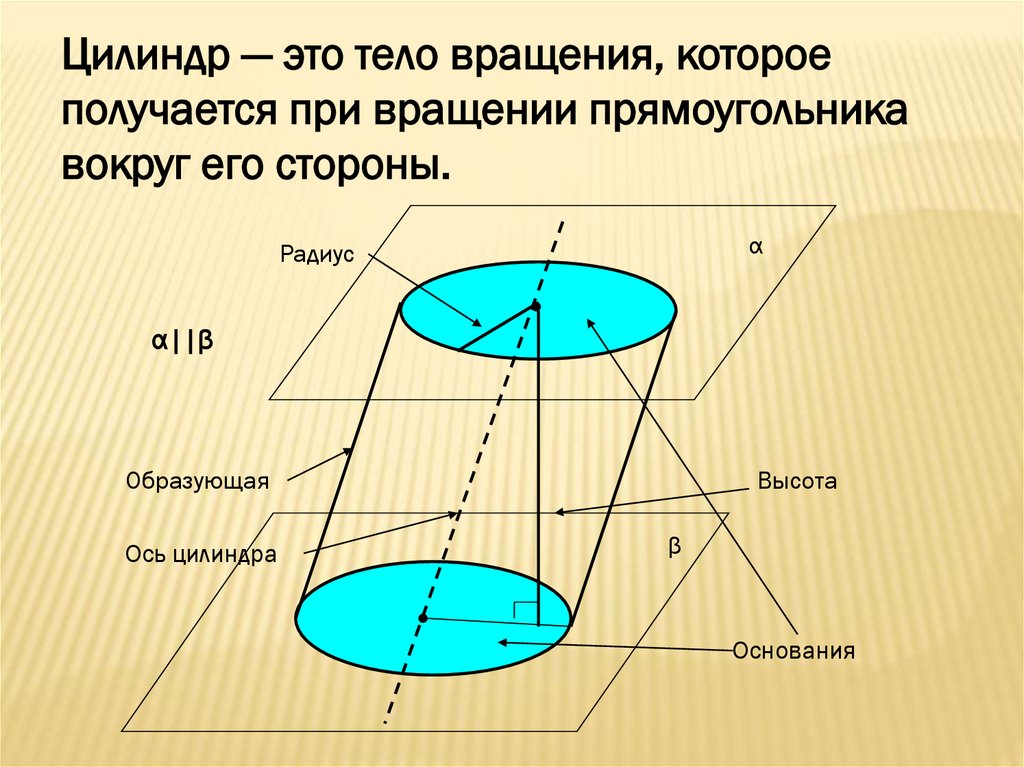
Цилиндр — это тело вращения, которое
получается при вращении прямоугольника
вокруг его стороны.
α
Радиус
α||β
Образующая
Ось цилиндра
Высота
β
Основания

3.

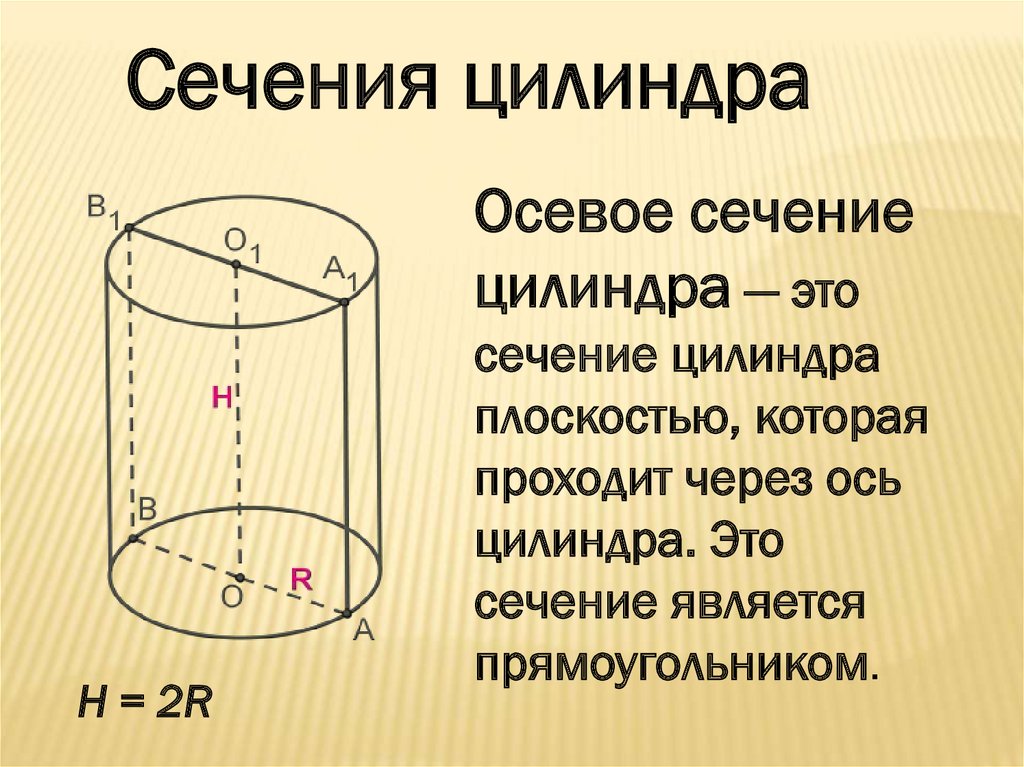
Сечения цилиндра
Осевое сечение
цилиндра — это
H = 2R
сечение цилиндра
плоскостью, которая
проходит через ось
цилиндра. Это
сечение является
прямоугольником.

4.

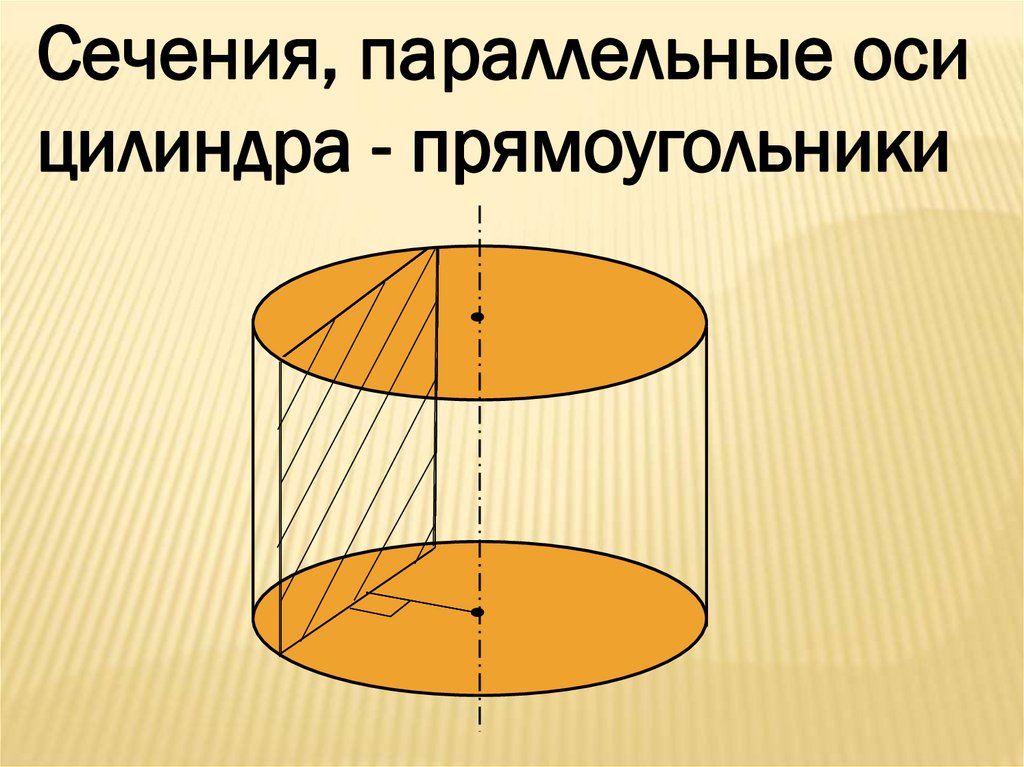
Сечения, параллельные оси
цилиндра - прямоугольники

5.

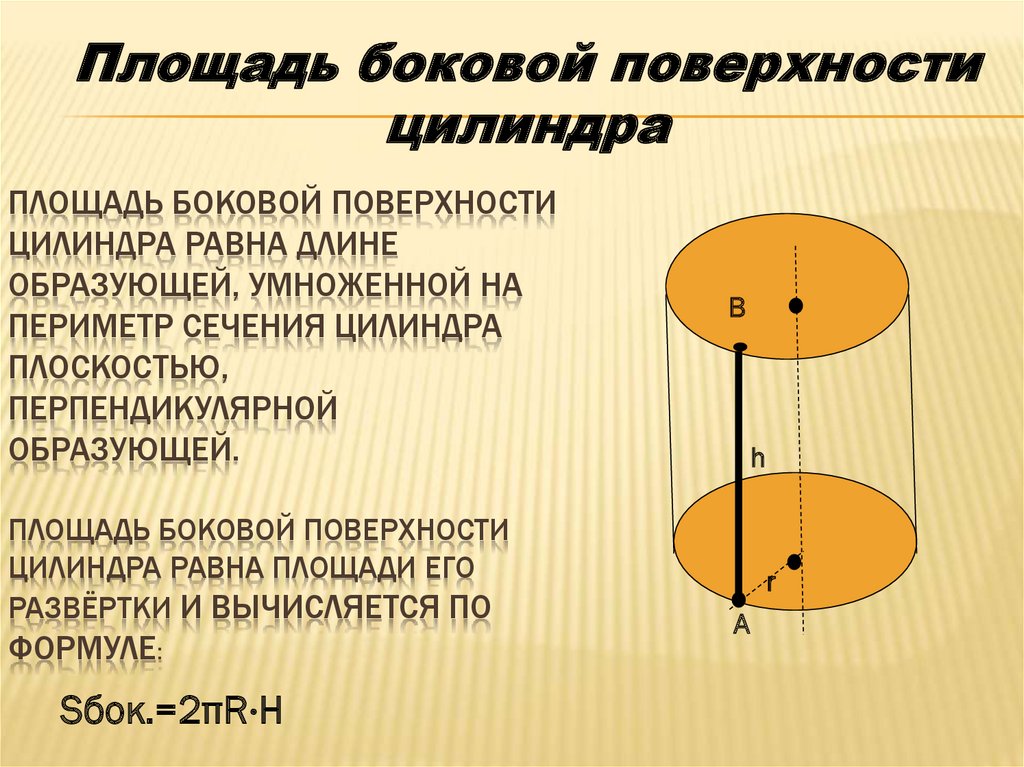
Площадь боковой поверхности
цилиндра
ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ
ЦИЛИНДРА РАВНА ДЛИНЕ
ОБРАЗУЮЩЕЙ, УМНОЖЕННОЙ НА
ПЕРИМЕТР СЕЧЕНИЯ ЦИЛИНДРА
ПЛОСКОСТЬЮ,
ПЕРПЕНДИКУЛЯРНОЙ
ОБРАЗУЮЩЕЙ.
ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ
ЦИЛИНДРА РАВНА ПЛОЩАДИ ЕГО
РАЗВЁРТКИ И ВЫЧИСЛЯЕТСЯ ПО
ФОРМУЛЕ:
Sбок.=2πR⋅H
В
h
r
А

6.

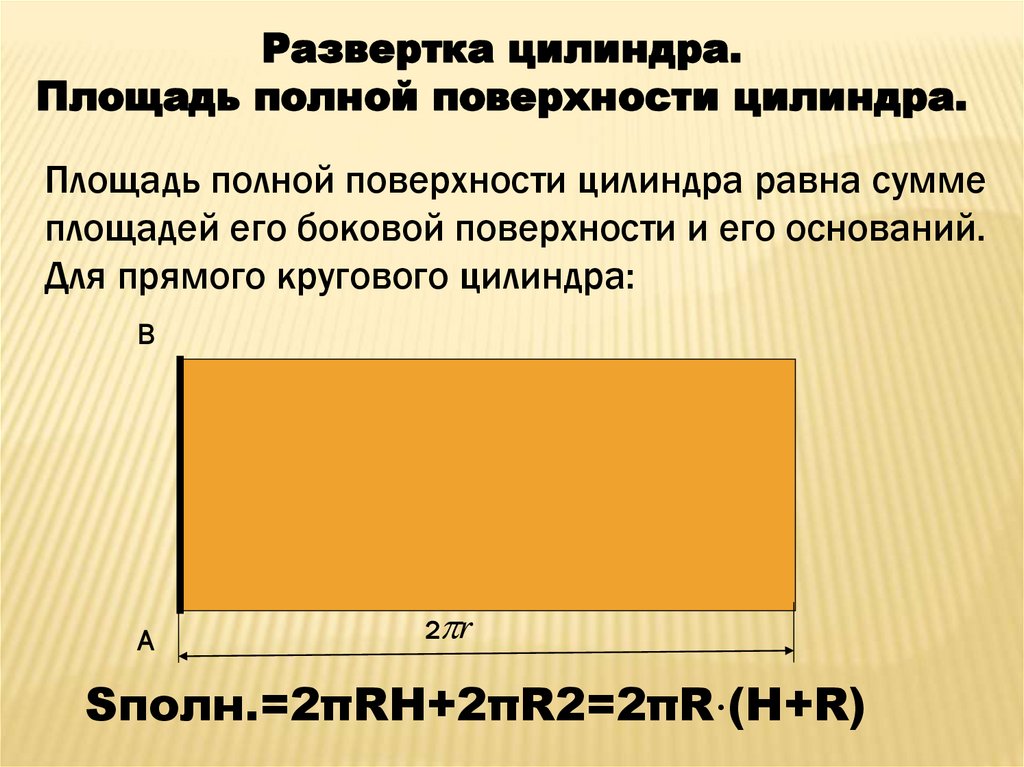
Развертка цилиндра.
Площадь полной поверхности цилиндра.
Площадь полной поверхности цилиндра равна сумме
площадей его боковой поверхности и его оснований.
Для прямого кругового цилиндра:
В
А
2 r
Sполн.=2πRH+2πR2=2πR⋅(H+R)

7.

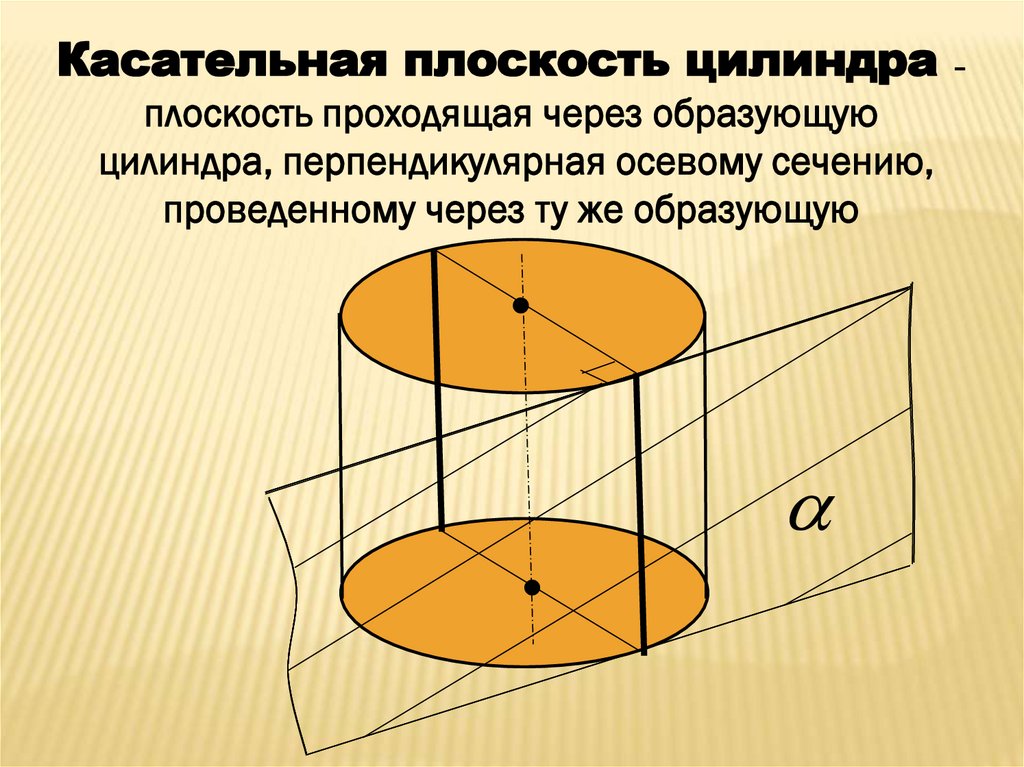
Касательная плоскость цилиндра
плоскость проходящая через образующую
цилиндра, перпендикулярная осевому сечению,
проведенному через ту же образующую
–

8.

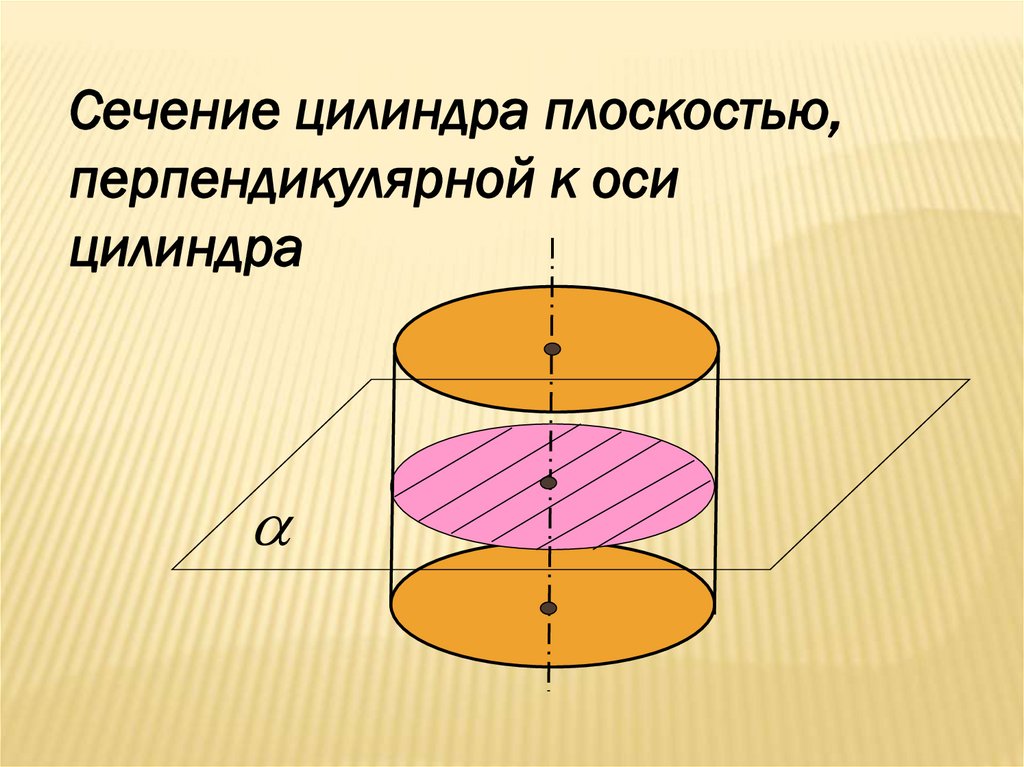
Сечение цилиндра плоскостью,
перпендикулярной к оси
цилиндра

9.

Для наклонного цилиндра
существуют две формулы:
1)Объём равен длине образующей, умноженной на
площадь сечения цилиндра плоскостью, перпендикулярной
образующей.
2)Объём равен площади основания, умноженной на высоту
(расстояние между плоскостями, в которых лежат
основания):
где — длина образующей, а
основания.
Для прямого цилиндра
Для кругового цилиндра:
— угол между образующей и плоскостью
,
и
,
и объём равен:
, где d — диаметр основания.

10.

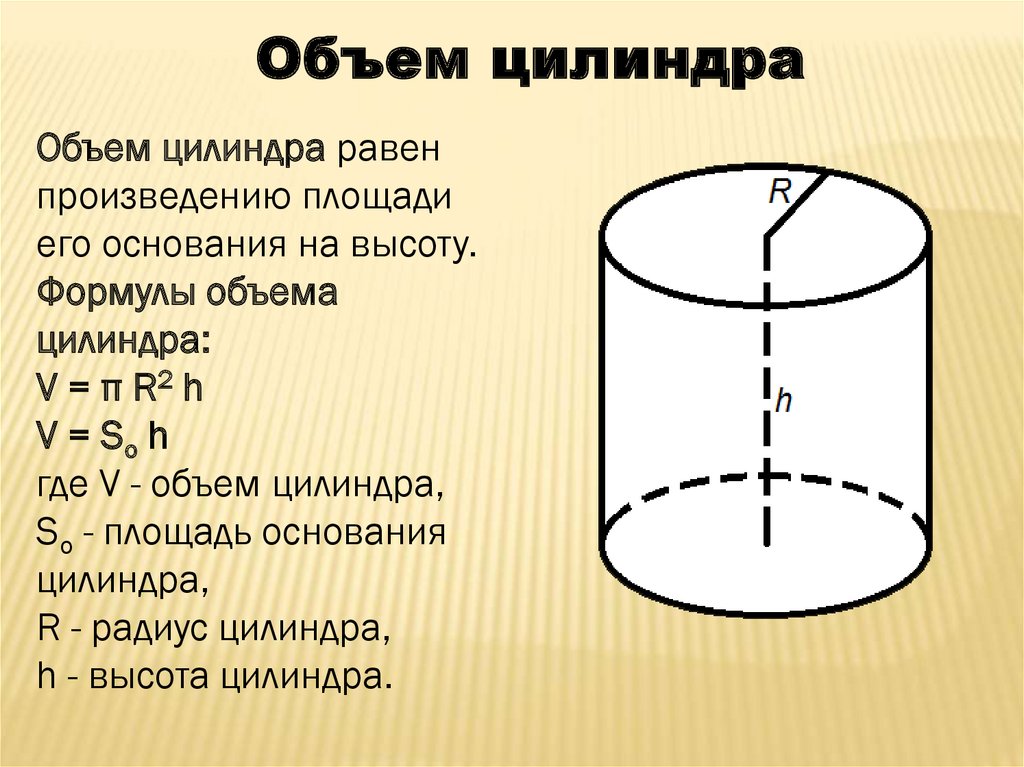
Объем цилиндра
Объем цилиндра равен
произведению площади
его основания на высоту.
Формулы объема
цилиндра:
V = π R2 h
V = So h
где V - объем цилиндра,
So - площадь основания
цилиндра,
R - радиус цилиндра,
h - высота цилиндра.