Похожие презентации:
Цилиндр. Площадь поверхности цилиндра
1.
По теме: «Цилиндр. Площадьповерхности цилиндра».
2.
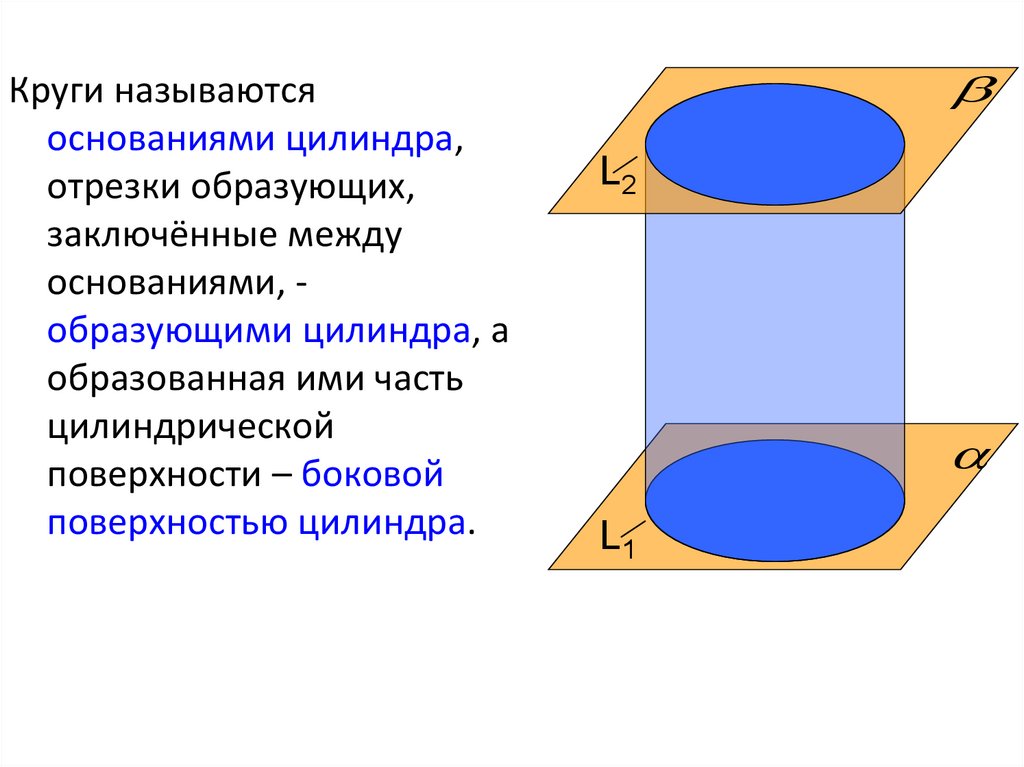
Круги называютсяоснованиями цилиндра,
отрезки образующих,
заключённые между
основаниями, образующими цилиндра, а
образованная ими часть
цилиндрической
поверхности – боковой
поверхностью цилиндра.
L2
L1
3.
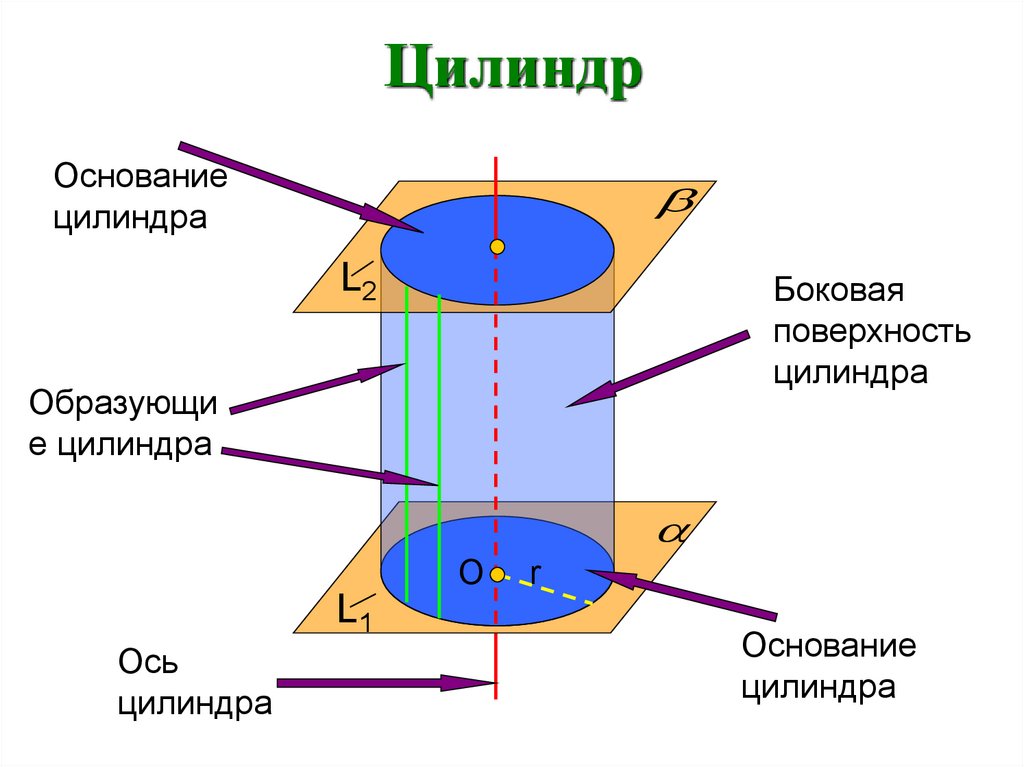
ЦилиндрОснование
цилиндра
L2
Боковая
поверхность
цилиндра
Образующи
е цилиндра
О
L1
Ось
цилиндра
r
Основание
цилиндра
4.
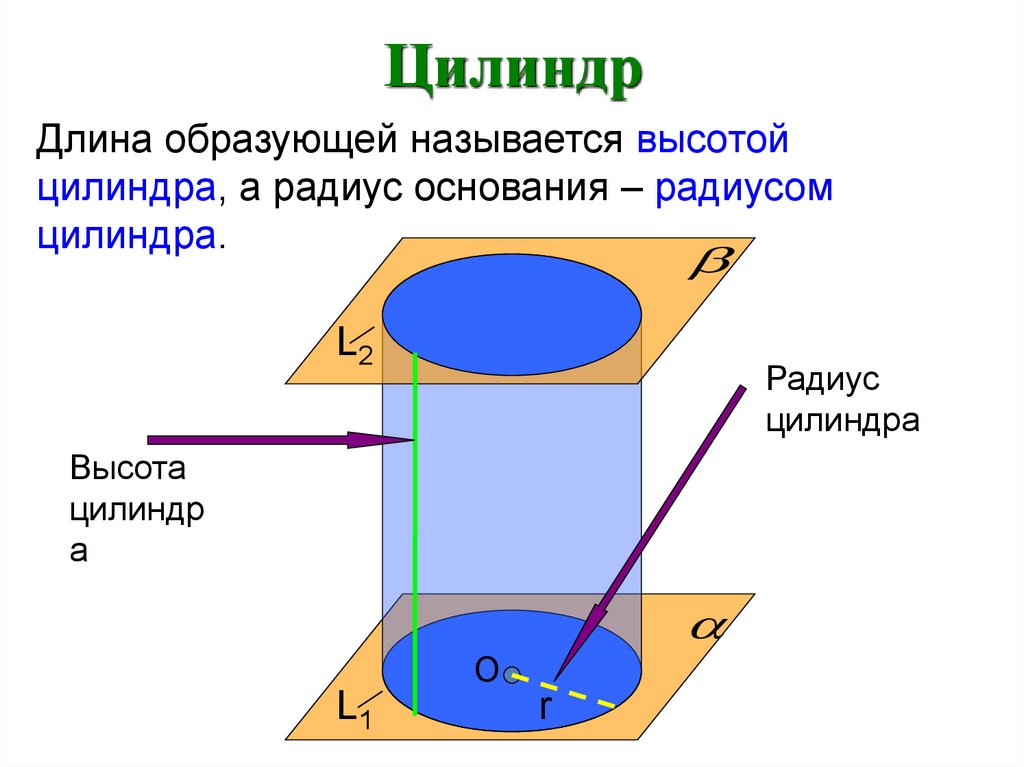
ЦилиндрДлина образующей называется высотой
цилиндра, а радиус основания – радиусом
цилиндра.
L2
Радиус
цилиндра
Высота
цилиндр
а
О
L1
r
5.
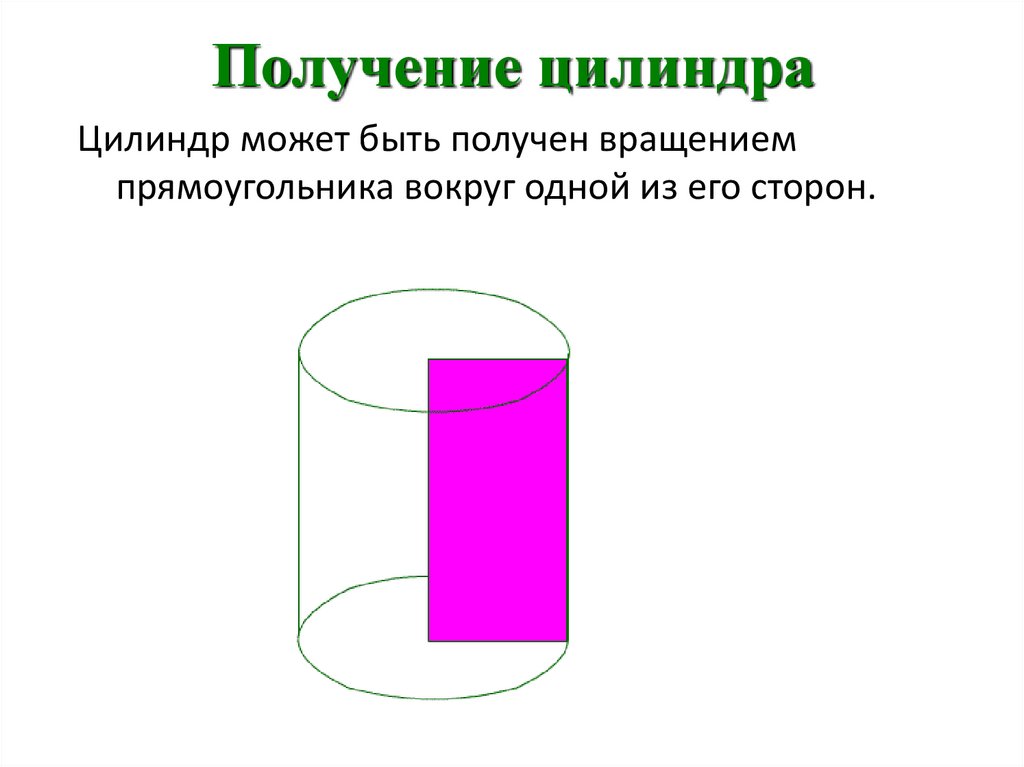
Получение цилиндраЦилиндр может быть получен вращением
прямоугольника вокруг одной из его сторон.
6.
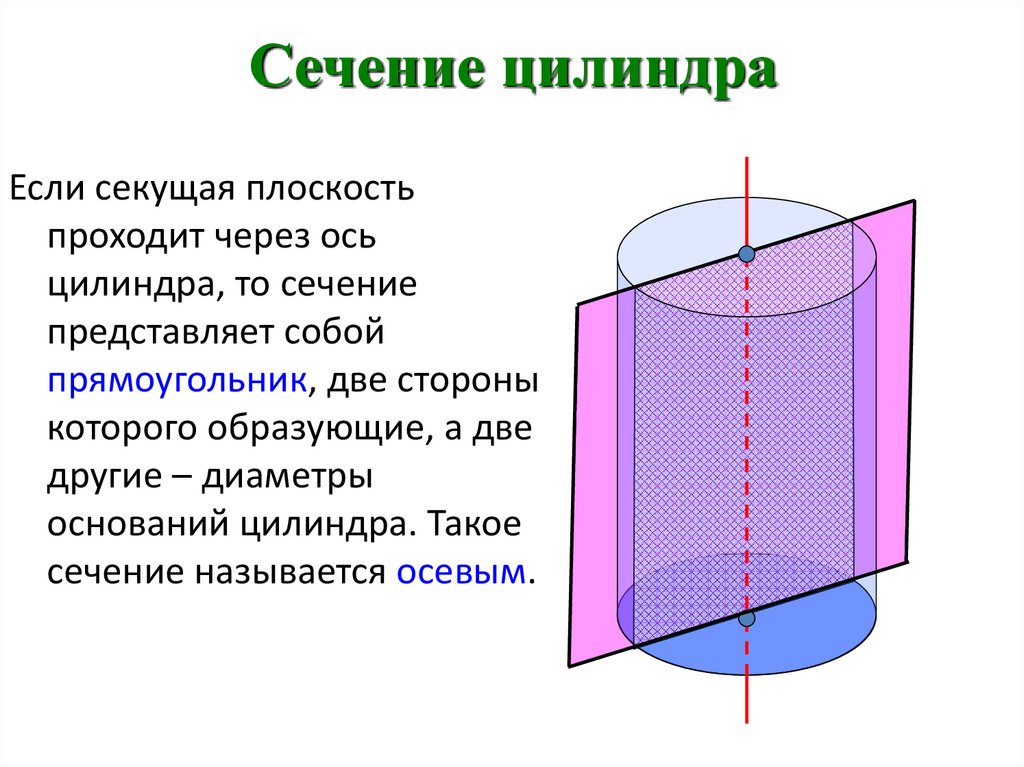
Сечение цилиндраЕсли секущая плоскость
проходит через ось
цилиндра, то сечение
представляет собой
прямоугольник, две стороны
которого образующие, а две
другие – диаметры
оснований цилиндра. Такое
сечение называется осевым.
7.
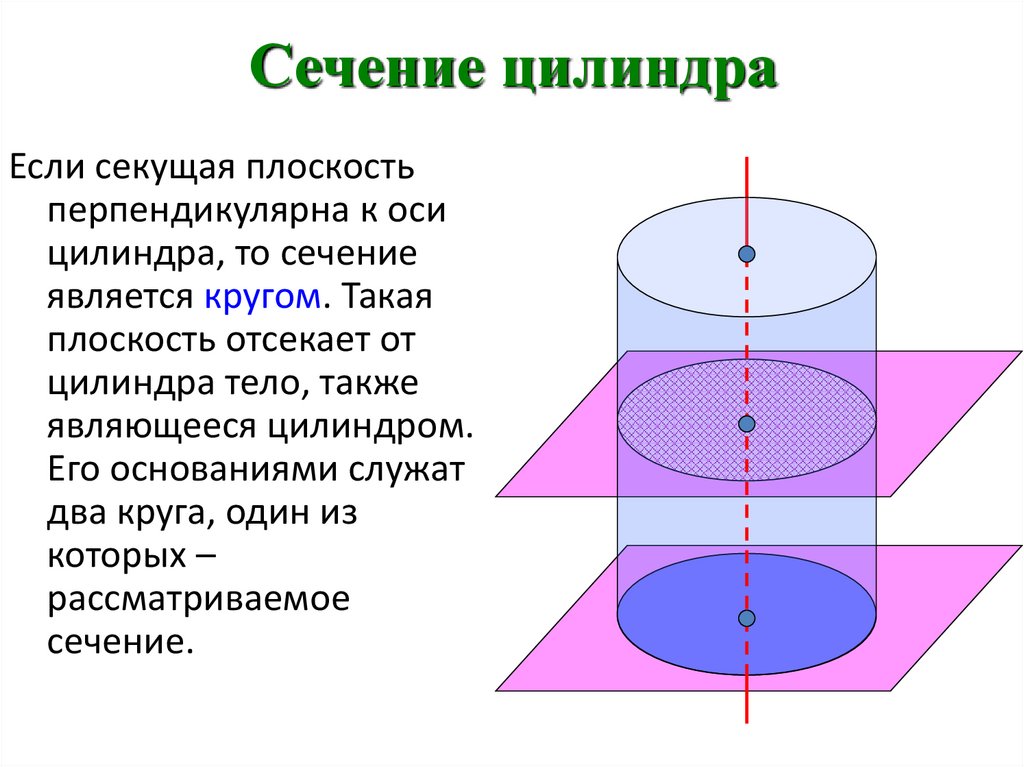
Сечение цилиндраЕсли секущая плоскость
перпендикулярна к оси
цилиндра, то сечение
является кругом. Такая
плоскость отсекает от
цилиндра тело, также
являющееся цилиндром.
Его основаниями служат
два круга, один из
которых –
рассматриваемое
сечение.
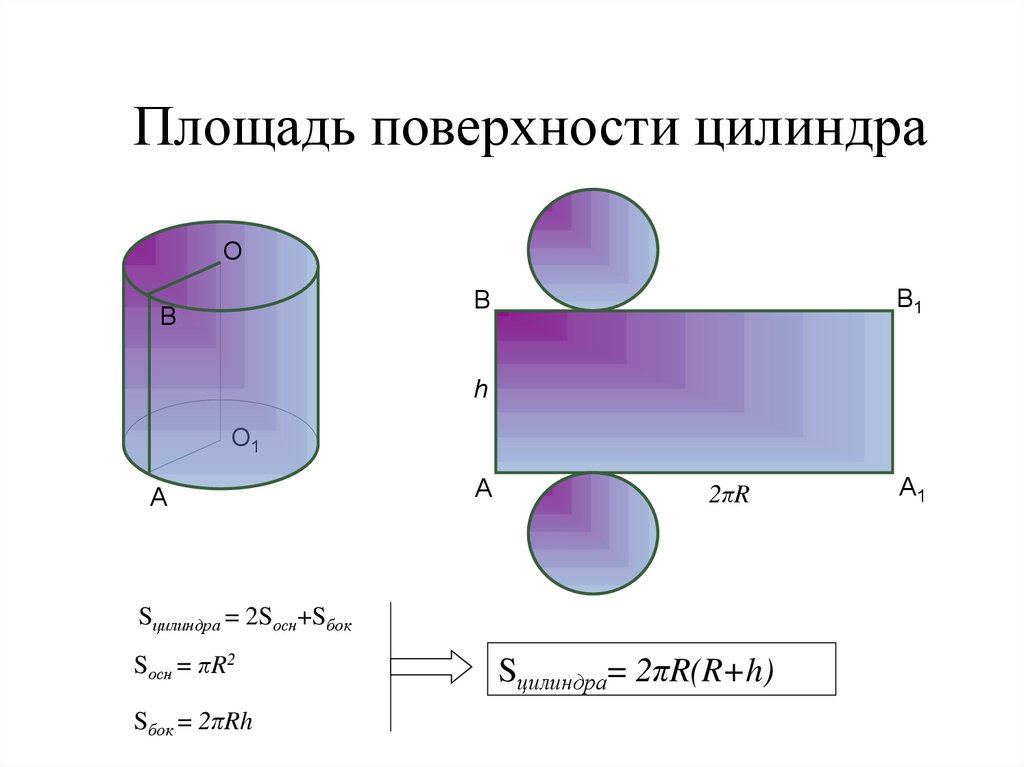
8. Площадь поверхности цилиндра
OB1
B
B
h
O1
A
A
2πR
Sцилиндра = 2Sосн+Sбок
Sосн = πR2
Sбок = 2πRh
Sцилиндра= 2πR(R+h)
A1
9.
Осевое сечение цилиндра – квадрат,диагональ которого равна 20 см. Найдите:
а) высоту цилиндра; б) So цилиндра
Решение.
B
C
1. Проведем диагональ АС
сечения АВСD.
2. ADC – равнобедренный,
прямоугольный, АD=DC, h = 2r,
45
20
CAD = ACD=45 , тогда
2
h AC cos 45 20
10 2 .
2
3. Найдем радиус основания
45
A
D
4. Найдем площадь основания
Ответ: а )10 2 ;
б )50 .
h 10 2
r
5 2.
2
2
2
So r 5 2 50 .
2
10.
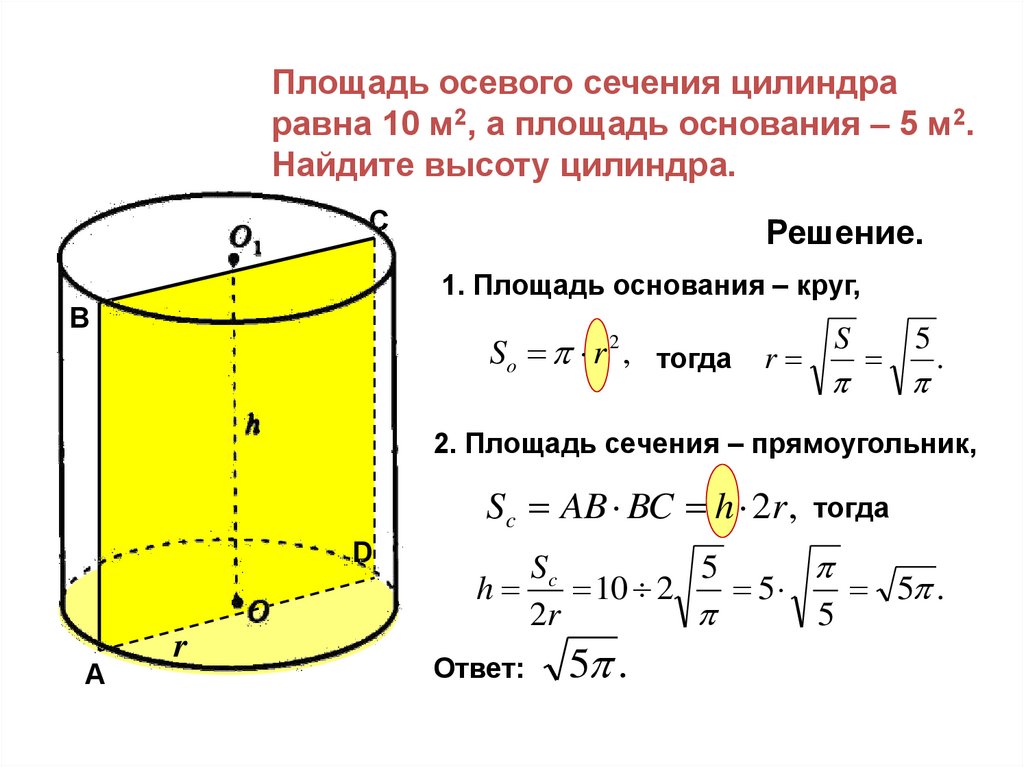
Площадь осевого сечения цилиндраравна 10 м2, а площадь основания – 5 м2.
Найдите высоту цилиндра.
C
Решение.
1. Площадь основания – круг,
B
So r 2 , тогда r S 5 .
2. Площадь сечения – прямоугольник,
Sc AB BC h 2r ,
D
A
r
тогда
Sc
5
h
10 2
5
5 .
2r
5
Ответ:
5 .


 Математика
Математика








