Похожие презентации:
Квадратные уравнения. Обобщающий урок. 8 класс
1.
Подготовила : учитель математикиМОУ «СОШ с. Марьино – Лашмино» Новобурасского района
Саратовской области
Майорова Любовь Александровна
2.
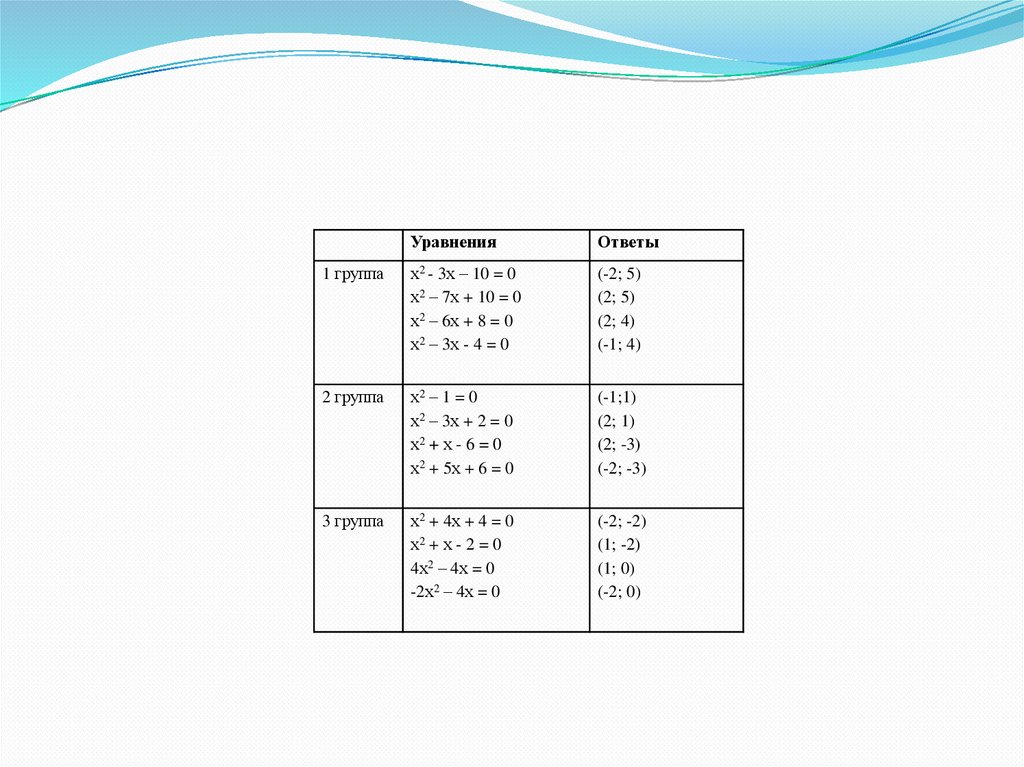
УравненияОтветы
1 группа
х2 - 3х – 10 = 0
х2 – 7х + 10 = 0
х2 – 6х + 8 = 0
х2 – 3х - 4 = 0
(-2; 5)
(2; 5)
(2; 4)
(-1; 4)
2 группа
х2 – 1 = 0
х2 – 3х + 2 = 0
х2 + х - 6 = 0
х2 + 5х + 6 = 0
(-1;1)
(2; 1)
(2; -3)
(-2; -3)
3 группа
х2 + 4х + 4 = 0
х2 + х - 2 = 0
4х2 – 4х = 0
-2х2 – 4х = 0
(-2; -2)
(1; -2)
(1; 0)
(-2; 0)
3.
1 группаУравнения
2х2 + 4х – 7 = 0
9х2 – 6х + 9 = 0
5х2 – 2х = 0
7х2 + 10х - 9 = 0
2 группа
3х2 – 6х = 0
-х2 + 9 = 0
2х2 + 5х = 0
х2 - 6х - 7 = 0
3 группа
х2 - 3х + 4 = 0
-5х2 - х + 1 = 0
х2 + 6х + 7 = 0
х2 + 5х + 12 = 0
4.
Уравненияполное
неполное
приведённое
неприведённое
х2 + 8х+3=0
2
6х + 9= 0
х2 – 3х = 0
-х2 + 2х + 4 = 0
3х + 6х2 +7 = 0
Уравнения
х2 + 8х =0
6х 2 + 9х -7 = 0
х 2– 3х + 15 = 0
-х2 - 3х + 14 = 0
3х 2 - 6х = 0
полное
неполное
приведённое
неприведённое
5.
Уравненияполное
неполное
приведённое
неприведённое
х2 + 8х+3=0
2
6х + 9= 0
х2 – 3х = 0
-х2 + 2х + 4 = 0
3х + 6х2 +7 = 0
Уравнения
х2 + 8х =0
6х 2 + 9х -7 = 0
х 2– 3х + 15 = 0
-х2 - 3х + 14 = 0
3х 2 - 6х = 0
полное
неполное
приведённое
неприведённое
6.
Не решая уравнениех2 −8х + 7 = 0.
Найдите:
а) сумму корней:
б) произведение корней:
в) корни данного уравнения:
7.
Задача знаменитого математика12 века Бхаскары (1114-ок. 1178)
Обезьянок резвых стая
Всласть поевши,
развлекалась.
Их в квадрате часть восьмая
На поляне забавлялась.
А двенадцать по лианам
Стали прыгать, повисая.
Сколько ж было обезьянок,
Ты скажи мне, в этой стае?
8.
Проверь себя:2
х
12 х
8
х2
12 х
64
х 2 12 64 64 х
х 2 64 х 768 0
D 4096 3072 1024
х1 64 322 48;
х2 64 322 16.
Ответ: 48 или 16 обезьянок.
9.
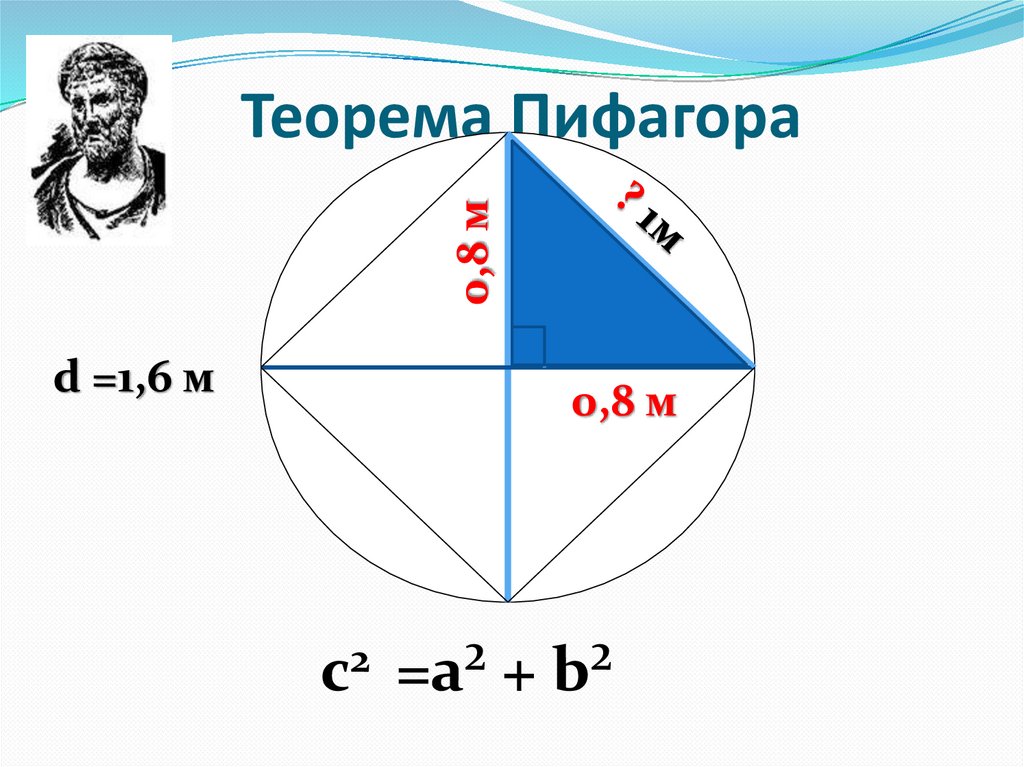
Можно ли в котлован круглой формыдиаметром 1,6 м поместить ёмкость для
бассейна прямоугольной формы со
сторонами, равными корням данного
уравнения?
х2 – 2х + 1 = 0
10.
11.
0,8 мТеорема Пифагора
d =1,6 м
0,8 м
2
с
=a² + b²
12.
Квадратные уравнения в Багдаде (9 век):Впервые квадратные уравнения
появились в городе Багдаде, их вывел
приглашённый математик из
Хорезм(Ныне территория Узбекистана)
Мухаммед бен-Муса Ал-Хорезми. В
отличие от греков, решавших
квадратные уравнения геометрическим
путем, он мог решить любые квадратные
уравнения по общему правилу (найти
положительные корни). Если у греков
было геометрическое решение, то метод
Ал-Хорезми почти алгебраический.
13.
Квадратные уравнения в Древнем Вавилоне:Необходимость решать уравнения не только первой, но и второй
степени ещё в древности была вызвана потребностью решать
задачи, связанные с нахождением площадей земельных участков и с
земляными работами военного характера, а так же с развитием
астрономии и самой математики. Квадратные уравнения умели
решать около 2000 лет до нашей эры вавилоняне. Применяя
современную алгебраическую запись, можно сказать, что в их
клинописных текстах встречаются, кроме неполных, и такие,
например, полные квадратные уравнения:
х2 + х =
х2 ─ х =
3
.
4
1
14 .
2
Правило решения этих уравнений, изложенное в вавилонских
текстах, совпадает с современным, однако неизвестно, каким
образом дошли вавилоняне до этого правила, Почти все найденные
до сих пор клинописные тексты, приводя только задачи с
решениями, изложенными в виде рецептов, без указаний
относительно того, каким образом они были найдены, Несмотря на
высокий уровень развития алгебры в Вавилонии, в клинописных
текстах отсутствует понятие отрицательного числа и общие методы
решения квадратных уравнений.
14.
Квадратные уравнения в ИндииЗадачи на квадратные уравнения встречаются уже в 499 году.
В Древней Индии были распространены публичные соревнования в
решении трудных задач.
В одной из старинных индийских книг говорится по поводу таких
соревнований следующее: “Как солнце блеском своим затмевает звёзды, так
учёный человек затмит славу другого в народных собраниях, предлагая и решая
алгебраические
задачи”.
15.
Квадратные уравнения в Европе в 13-17 веках:Формулы решения квадратных уравнений в Европе были
Впервые изложены в 1202 году итальянским математиком
Леонардо Фибоначчи.
Общее правило решения квадратных
уравнений, приведенных к единому
каноническому виду аx2 + bx + c = 0,было
Сформулировано в Европе лишь в 1544
Году немецким математиком
Михаэлем Штифелем.
16.
Виды квадратных уравненийНеполные квадратные уравнения и частные виды полных квадратных
Уравнений (х2 + х = а) умели решать Некоторые виды квадратных уравнений
решали древнегреческие математики, сводя их решение к геометрическим
построениям. Правило решения квадратных уравнений, приведенных к виду
aх2 + bx + c = 0, где а ≠ 0,дал индийский ученый Брахмагупта(7век).
Вывод формулы корней квадратного уравнения в общем виде имеется у Виета,
однако он признавал только положительные корни. Итальянские математики
16 веке учитывают помимо положительных и отрицательные корни. Лишь в 17
веке благодаря трудам Жирара, Декарта, Ньютона и других учёных
способ решения квадратных уравнений принимает современный вид.
17.
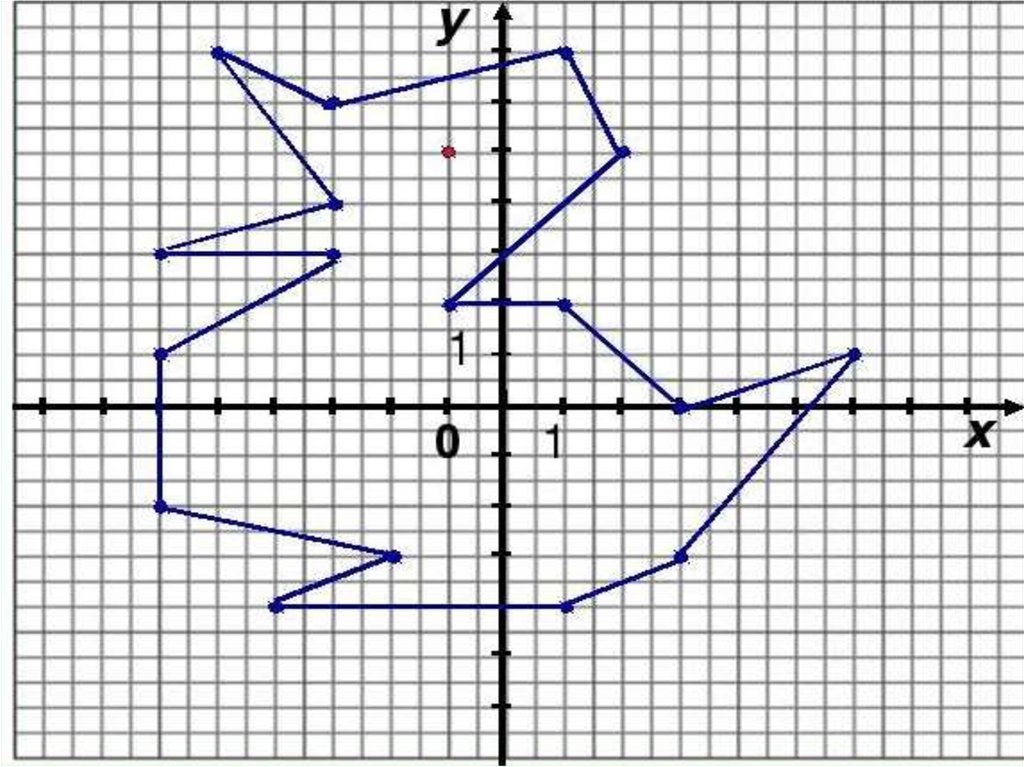
1)(3;0) 2)(6;1) 3) (3;-3) 4) (1;-4) 5)(-4;-4) 6) (-2;-3) 7)( 6;-2)8) (-6;1) 9) (-2;3) 10) (-6;3) 11) (-3;4) 12)(-5;7) 13) (-3;6)
14) (1;7) 15) (2;5) 16) (-1;2) 17) (1;2) 18) (-1;5)
18.
19.
Дан участок прямоугольнойформы, площадь которого 135 м2.
Найти стороны этого участка,
если известно, что одна сторона
больше другой на 6 м.
х (х+6)=135
























 Математика
Математика








