Абсолютные и относительные величины

1.

АБСОЛЮТНЫЕ И ОТНОСИТЕЛЬНЫЕ
ВЕЛИЧИНЫ

2.

ВОПРОСЫ ТЕМЫ
1. Сущность статистических
показателей Абсолютные
величины
2. Относительные величины

3.

Статистический показатель
обобщенная количественнокачественную характеристика
свойства группы единиц или всей
совокупности в целом в условиях
конкретного места и времени

4.

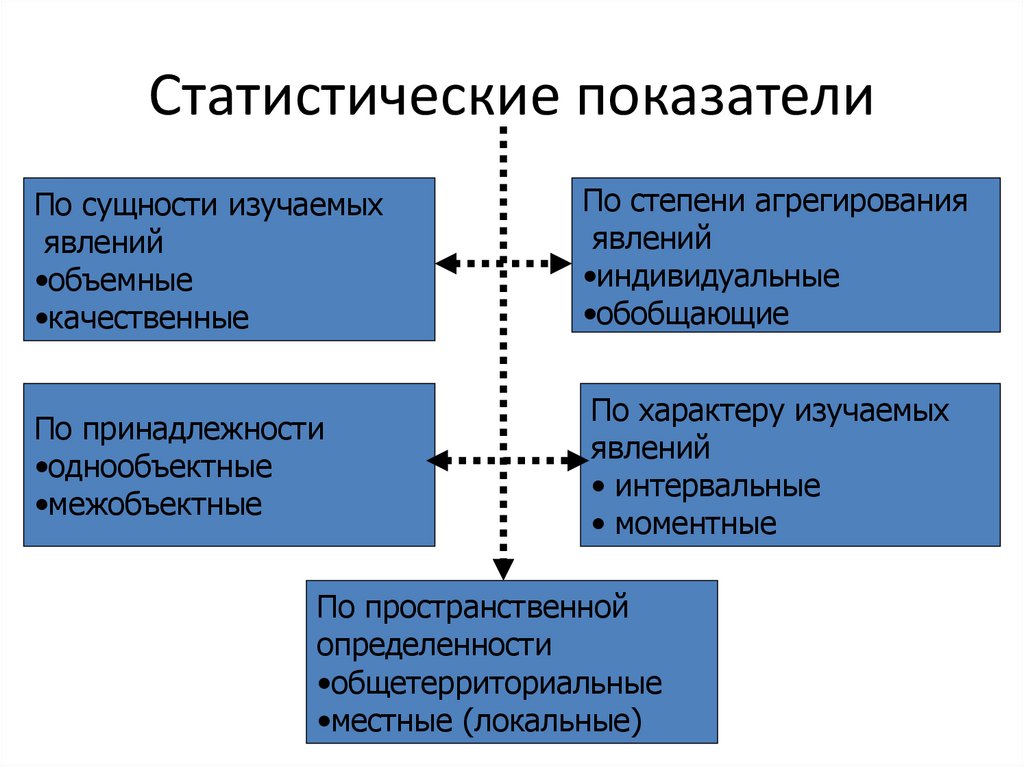
Статистические показатели
По сущности изучаемых
явлений
•объемные
•качественные
По степени агрегирования
явлений
•индивидуальные
•обобщающие
По принадлежности
•однообъектные
•межобъектные
По характеру изучаемых
явлений
• интервальные
• моментные
По пространственной
определенности
•общетерриториальные
•местные (локальные)

5.

СТАТИСТИЧЕСКИЙ
ПОКАЗАТЕЛЬ
ЧИСЛЕННОЕ
ЗНАЧЕНИЕ
ВЕЛИЧИНА
ПОКАЗАТЕЛЯ

6.

Абсолютные статистические
величины
показатели, которые выражают
размеры, объемы и уровни явлений
и процессов

7.

По способу выражения
абсолютные величины
подразделяются на
• индивидуальные
• суммарные

8.

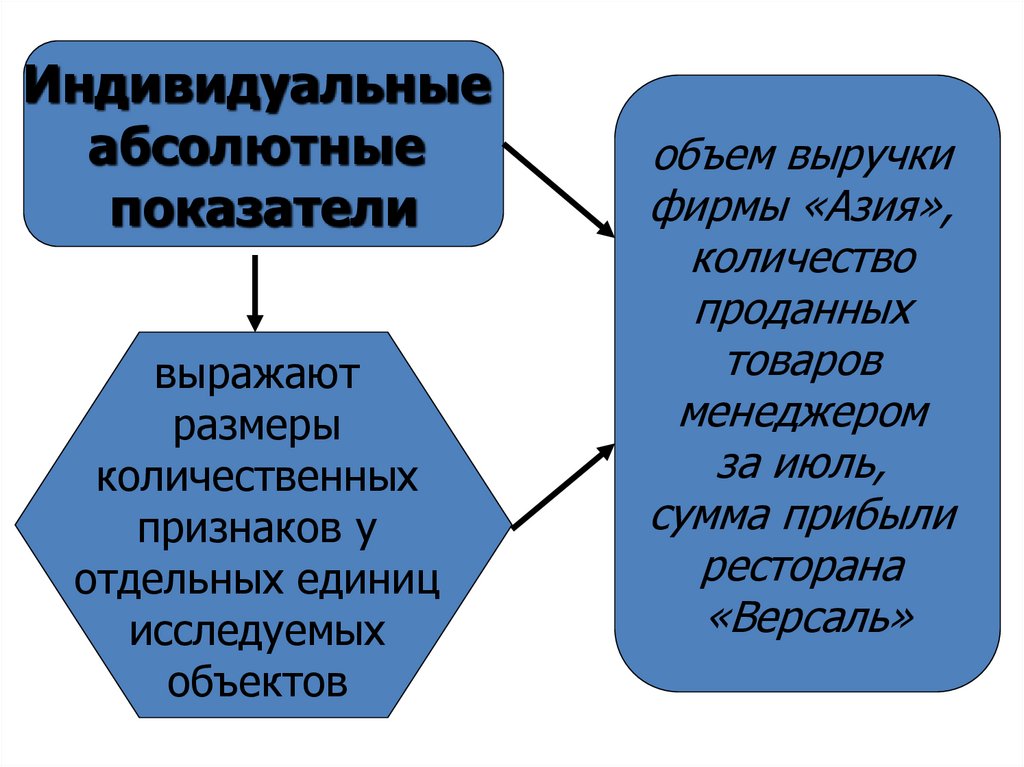
Индивидуальные
абсолютные
показатели
выражают
размеры
количественных
признаков у
отдельных единиц
исследуемых
объектов
объем выручки
фирмы «Азия»,
количество
проданных
товаров
менеджером
за июль,
сумма прибыли
ресторана
«Версаль»

9.

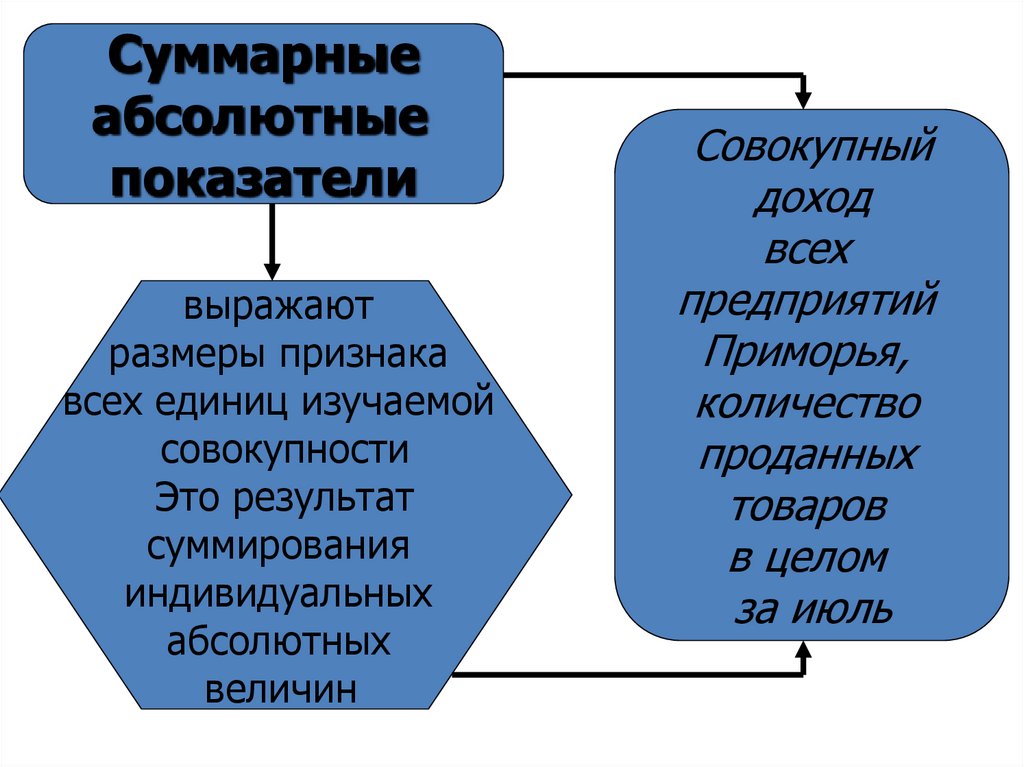
Суммарные
абсолютные
показатели
выражают
размеры признака
всех единиц изучаемой
совокупности
Это результат
суммирования
индивидуальных
абсолютных
величин
Совокупный
доход
всех
предприятий
Приморья,
количество
проданных
товаров
в целом
за июль

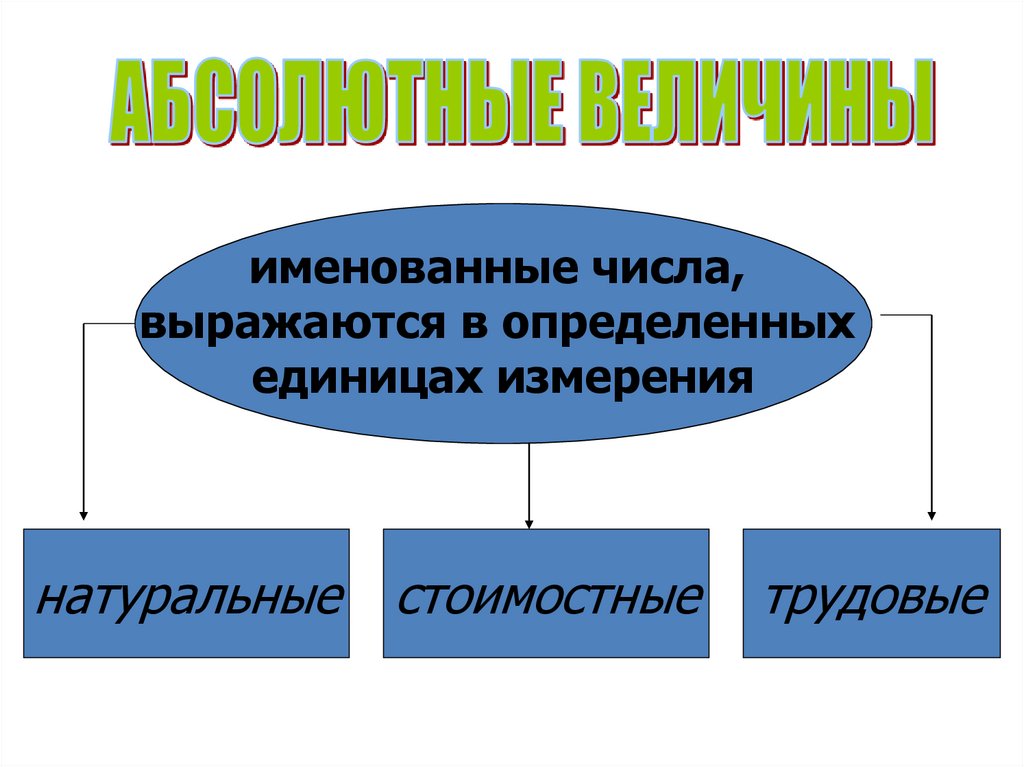
10.

именованные числа,
выражаются в определенных
единицах измерения
натуральные стоимостные
трудовые

11.

Относительные
статистические величины
показатели, которые раскрывают
числовую меру соотношения двух
сопоставляемых статистических
величин

12.

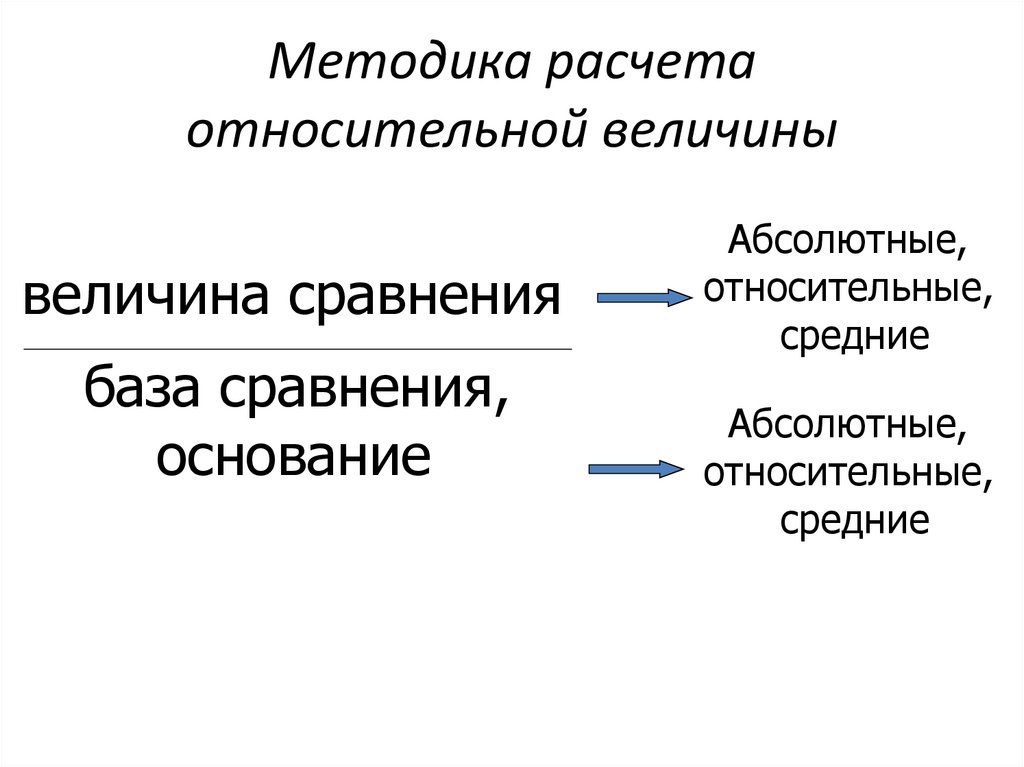
Методика расчета
относительной величины
величина сравнения
база сравнения,
основание
Абсолютные,
относительные,
средние
Абсолютные,
относительные,
средние

13.

Единицы измерения
относительных величин
Например: в 2017 г. число
фирм составляло 1300 единиц, а в 2018 году
1500
1500
1300
1500
1300
1,15
КОЭФФИЦИЕНТ
1,15 *100=115%
В
ПРОЦЕНТАХ

14.

Единицы измерения
относительных величин
Например: число туристических фирм 3000,
число жителей региона 2 млн. чел.
3000 *100000=150 фирм на каждые
100000 тыс. человек
2000000
ИМЕНОВАННОЕ
ЧИСЛО

15.

• Динамики (ОВД)
• Плана (ОВП)
• Реализации плана (ОВРП)
• Структуры (ОВС)
• Координации (ОВК)
• Интенсивности и уровня экономического
развития (ОВИ)
• Сравнения (ОВСр)

16.

ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА
ДИНАМИКИ
характеризует изменение
одноименных явлений во времени и
получается в результате
сопоставления показателей
каждого последующего периода с
предыдущим (цепная), или
первоначальным (базисная)

17.

ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА
ДИНАМИКИ
ОВД = Показатель текущего периода
Показатель предшествующего
или базисного периода

18.

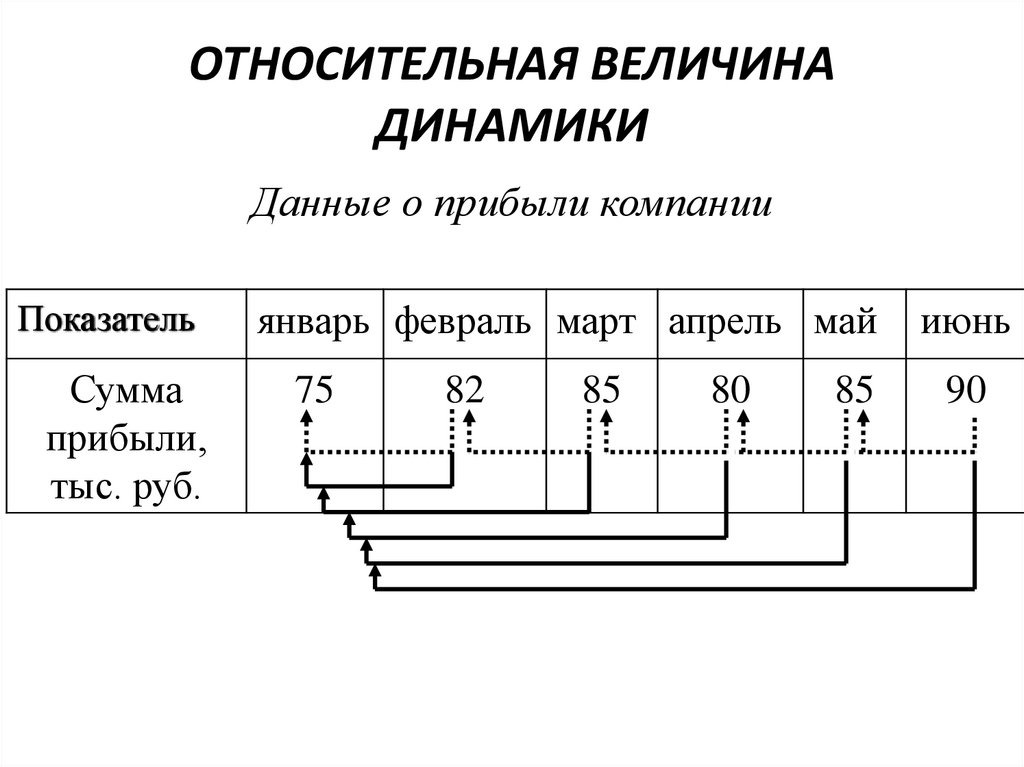
ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА
ДИНАМИКИ
Данные о прибыли компании
Показатель
Сумма
прибыли,
тыс. руб.
январь февраль март апрель май
75
82
85
80
85
июнь
90

19.

ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА ПЛАНА
показывает, какое планируется
изменение показателей по сравнению
с базисным периодом, и
определяются как отношение
планового задания на предстоящий
период к фактически достигнутому
уровню за предшествующий период

20.

ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА ПЛАНА
ОВП= План на предстоящий период
Факт за базисный период

21.

ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА
РЕАЛИЗАЦИИ ПЛАНА
выражает уровень выполнения
планового задания по какому-либо
показателю в виде отношения
фактической величины показателя к
плановой величине

22.

ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА
РЕАЛИЗАЦИИ ПЛАНА
ОВРП= Факт за отчетный период
План на данный период
ВЗАИМОСВЯЗЬ: ОВП*ОВРП=ОВД

23.

ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА ПЛАНА И
РЕАЛИЗАЦИИ ПЛАНА
Например:
•прибыль компании экспортера в 2017 году
-550 т. р;
•руководство запланировало получить в
следующем году прибыль - 670 т. р.;
•фактически в 2008 году прибыль - 650 т. р.

24.

ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА ПЛАНА И
РЕАЛИЗАЦИИ ПЛАНА
ОВП = 670/550*100= 122,0% запланировали увеличить
прибыль на 22 %
ОВРП = 650/670*100=97,0% план не выполнен на 3%

25.

ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА
СТРУКТУРЫ
характеризует состав, структуру изучаемой
совокупности и показывает, какой удельный
вес, или какую долю в общем итоге
совокупности составляет каждая ее часть.
Рассчитывается делением значения каждой
части совокупности на их общий итог,
принятый за базу для сравнения. Сумма
относительных величин структуры изучаемой
совокупности всегда равна 100%, или 1

26.

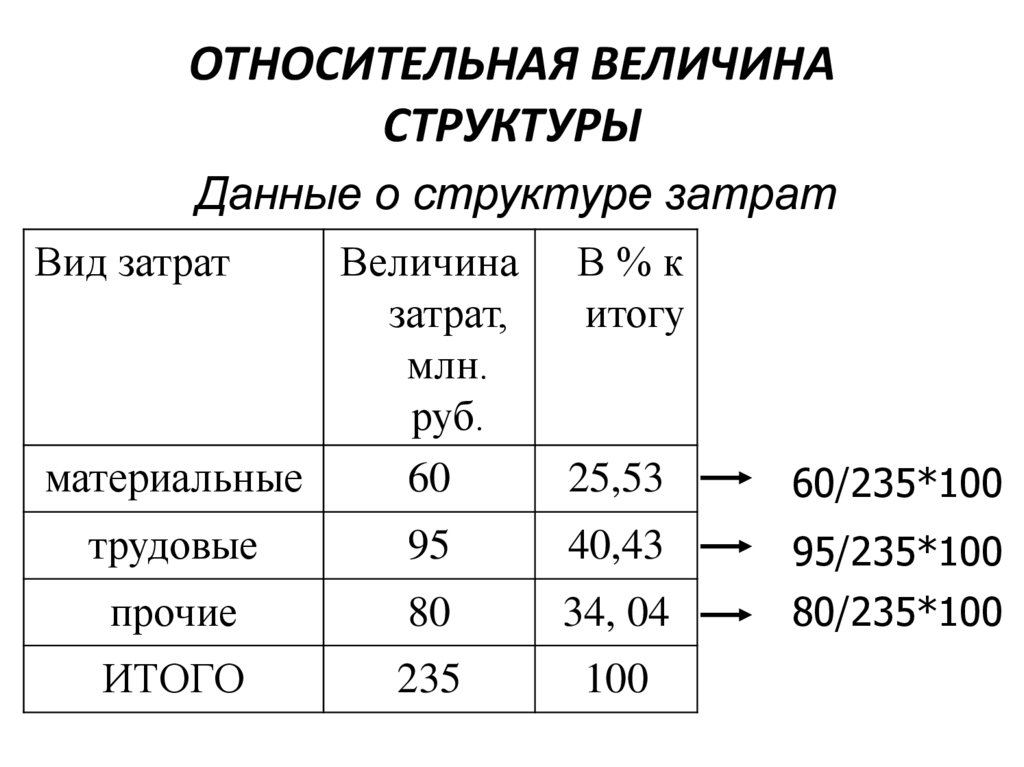
ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА
СТРУКТУРЫ
Данные о структуре затрат
Вид затрат
Величина
затрат,
млн.
руб.
материальные
60
В%к
итогу
25,53
60/235*100
трудовые
95
40,43
95/235*100
прочие
80
34, 04
80/235*100
ИТОГО
235
100

27.

ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА
КООРДИНАЦИИ
характеризует соотношение отдельных
частей целого, одна из которых
принимается за базу для сравнения. В
результате получают, сколько единиц
каждой структурной части приходится на 1
единицу (100, 1000 и т.д.) базисной
структурной части. Данная величина
является именованной

28.

ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА
КООРДИНАЦИИ
ОВК = i-ая часть совокупности
часть совокупности,
выбранная базой сравнения

29.

ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА
КООРДИНАЦИИ
Например:
•численность мужчин – 1200 человек;
•численность женщин – 2400 человек.
Рассчитаем ОВК, используя базой
сравнения численность мужчин.
ОВК = 2400/1200=2 человека,
то есть, на каждого работника мужчину
приходится две женщины.

30.

ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА
ИНТЕНСИВНОСТИ
характеризует степень
распространенности изучаемого
явления в определенной среде.
Данная величина является
именованной

31.

ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА
ИНТЕНСИВНОСТИ
ОВИ = Показатель, характеризующий
явление Х
Показатель, характеризующий
среду распространения явления Х

32.

ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА
ИНТЕНСИВНОСТИ
Например:
•число койко-мест в санаториях – 3250
•число жителей – 2500 тыс. чел.
Рассчитаем относительную величину
интенсивности в расчете на 10000 человек.
ОВИ= 3250/2500000*10000=13 мест,
то есть на каждую тысячу жителей
приходится 13 койко-мест

33.

ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА
СРАВНЕНИЯ
позволяет сопоставить
одноименные величины,
относящиеся к различным
объектам и оценить какая
величина и на сколько больше
либо меньше другой

34.

ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА
СРАВНЕНИЯ
ОВСр = Показатель по объекту А
Показатель по объекту Б

35.

ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА
СРАВНЕНИЯ
Например:
•численность студентов группы БУ-06 - 20
человек
•численность студентов БУ-07 - 17 человек.
Рассчитаем ОВСр, используя в качестве базы
сравнения численность студентов группы БУ-06
ОВСР = 17/20*100= 85%
численность студентов группы БУ-07 меньше
численности студентов группы БУ-06 на 15%

36.

Тема: Средние величины

37.

Средняя величина
Обобщающий показатель, который
дает количественную характеристику
признака в статистической
совокупности в условиях

38.

Условия правильного применения средней величины:
Средняя величина должна исчисляться лишь для совокупностей, состоящих из
однородных единиц
Совокупность, неоднородную в качественном отношении, необходимо разделять
на однородные группы и вычислять для них групповые типичные средние,
характеризующие каждую из этих групп. В этом проявляется связь между
методами группировок и средних величин
Средняя величина сглаживает индивидуальные значения и тем самым может
элиминировать различные тенденции в развитии, скрыть передовое и отстающее,
поэтому кроме средней величины следует исчислять другие показатели
Среднюю величину целесообразно исчислять не для отдельных единичных фактов,
взятых изолированно друг от друга, а для совокупности фактов

39.

Виды средних величин
Степенные
Структурные
Гармоническая
Мода
Геометрическая
Медиана
Арифметическая
Квартили
Квадратическая
Децили
Кубическая
Квинтили
Биквадратическая
Перцентили

40.

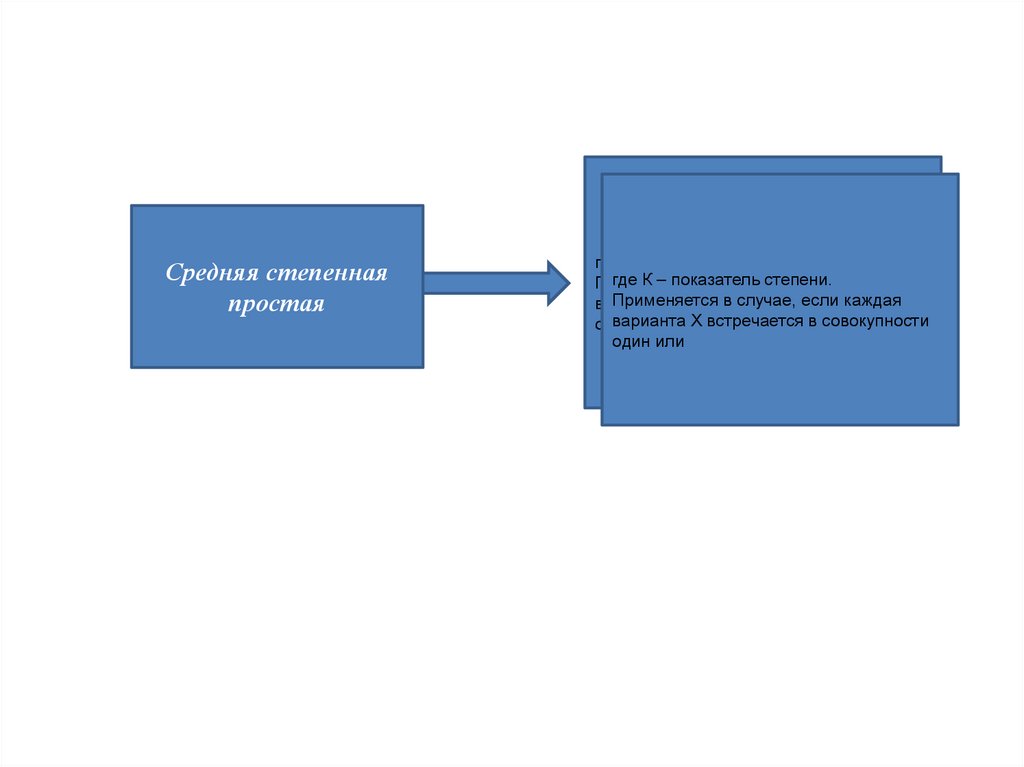
X
Средняя степенная
простая
K
X
K
n
где К – показатель степени.
где К – показатель
степени.
Применяется
в случае,
если каждая
Применяется
в
случае,
каждая
варианта Х встречается в если
совокупности
варианта
один
или Х встречается в совокупности
один или

41.

X f
X
f
K
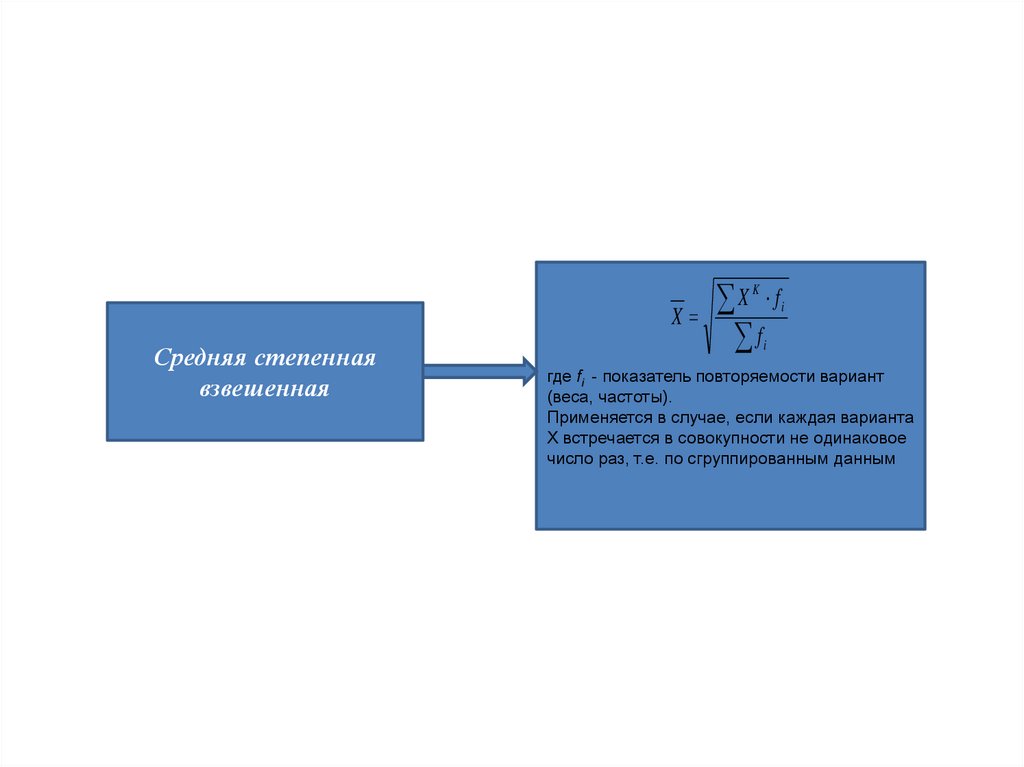
Средняя степенная
взвешенная
i
i
где fi - показатель повторяемости вариант
(веса, частоты).
Применяется в случае, если каждая варианта
Х встречается в совокупности не одинаковое
число раз, т.е. по сгруппированным данным

42.

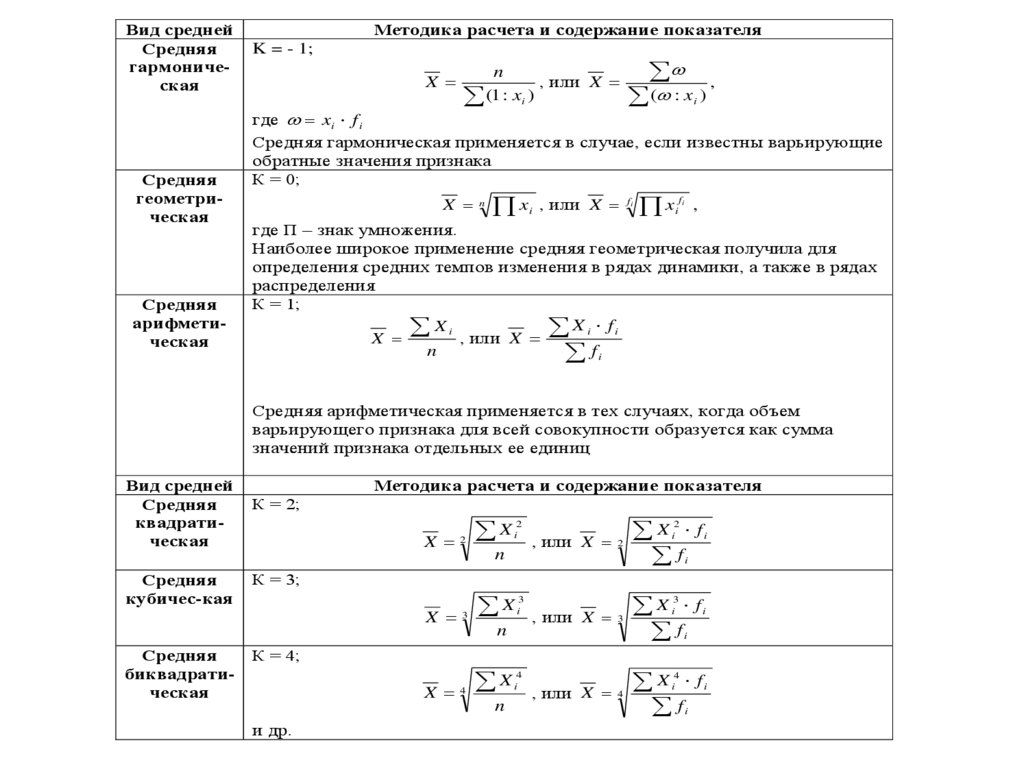
Вид средней
Средняя
гармоническая
Средняя
геометрическая
Средняя
арифметическая
Методика расчета и содержание показателя
K = - 1;
X
n
,
, или X
(1 : xi )
( : xi )
где xi f i
Средняя гармоническая применяется в случае, если известны варьирующие
обратные значения признака
К = 0;
X n xi , или X f i xif i ,
где П – знак умножения.
Наиболее широкое применение средняя геометрическая получила для
определения средних темпов изменения в рядах динамики, а также в рядах
распределения
К = 1;
X i , или X X i f i
X
n
fi
Средняя арифметическая применяется в тех случаях, когда объем
варьирующего признака для всей совокупности образуется как сумма
значений признака отдельных ее единиц
Вид средней
Средняя
квадратическая
Средняя
кубичес-кая
Средняя
биквадратическая
Методика расчета и содержание показателя
К = 2;
X
2
X
2
i
n
, или X
2
X f
f
2
i
i
i
К = 3;
X
3
X
3
i
n
, или X 3
X f
f
3
i
i
i
К = 4;
X 4
и др.
X
n
4
i
, или X 4
X f
f
4
i
i
i

43.

Основные свойства средней арифметической
Свойство
Произведение средней на сумму частот всегда равно
сумме произведений вариант частот
Если от каждой варианты отнять какое-либо
произвольное число, то средняя увеличится на это же
число
Если к каждой варианте прибавить какое-либо
произвольное число, то средняя увеличится на это же
число
Если каждую варианту разделить на какое-либо
произвольное число, то средняя арифметическая
уменьшится во столько же раз
Формула расчета
X fi X i fi
( X A) f X A
f
( X A) f X A
f
i
i
i
i
i
i
Xi
A f X
f
A
i
i
Если каждую варианту умножить на какое-либо
произвольное число, то средняя арифметическая
увеличится во столько же раз
Если все частоты (веса) разделить или умножить на
какое-либо число, то средняя арифметическая от этого
не изменится
Сумма отклонений вариант от средней арифметической
всегда равна нулю
( X A) f X A
f
X ( f A) X
( f A)
(X X ) f 0
i
i
i
i
i
i
i

44.

Мода
Величина признака (варианта),
которая чаще всего встречается
в данной совокупности. В
вариационном дискретном ряду
модой выступает варианта,
имеющая наибольшую частоту

45.

Медиана
варианта, которая находится в
середине вариационного ряда.
Медиана делит ряд пополам, по обе
стороны от нее (вверх и вниз)
находится одинаковое количество
единиц совокупности

46.

Виды структурных (непараметрических) средних
Вид
Средней
Мода
Методика расчета показателя
В интервальных рядах с равными интервалами мода вычисляется по
формуле
( f m f m 1 )
,
Mo X 0 i
( f m f m 1 ) ( f m f m 1 )
Где X0 – минимальная граница модального интервала;
i – величина модального интервала;
fm – частота модального интервала;
fm-1 – частота интервала, предшествующего модальному интервалу;
fm+1 – частота интервала, следующего за модальным.
Модальный интервал в интервальном ряду определяется по наибольшей
частоте

47.

Медиана
В дискретном вариационном ряду определение медианного значения
признака сводится к определению номера медианной единицы ряда по
формуле
n 1
N ME
,
2
где n – объем совокупности.
Полученное значение показывает, где точно находится номер медианной
единицы (номер середины ряда). Медианное значение характеризуется тем,
что его кумулятивная частота (сумма накопленных частот по группам) равна
половине суммы всех частот или превышает ее.
В интервальном ряду с равными интервалами медиана рассчитывается по
формуле
1
f S m 1
2
Me X 0 i
,
fm
где X0 – начальное значение медианного интервала;
i - величина медианного интервала;
∑f – сумма частот ряда;
Sm-1 - сумма накопленных частот в интервалах, предшествующих
медианному;
fm – частота медианного интервала.
Для определения медианного интервала необходимо рассчитать суммы
накопленных частот. Медианный интервал характерен тем, что его
кумулятивная частота равна полусумме всех частот ряда или превышает ее

48.

Квартили
Значения признака, делящие ранжированную совокупность на четыре
равные части. Различают нижний квартиль (Q1), отделяющий ¼ часть
совокупности с наименьшими значениями признака, и верхний квартиль
(Q3), отсекающий ¼ часть с наибольшими значениями признака. Средний
квартиль (Q2) совпадает с медианой (Me). Для расчета квартилей по
интервальному вариационному ряду используют формулы
1
f S Q1 1
4
;
Q1 X Q1 i
f Q1
3
f S Q3 1
4
,
Q3 X Q3 i
f Q3
где XQ (XQ ) – нижняя граница интервала, содержащего нижний квартиль
(верхний) квартиль;
i - величина интервала;
SQ -1 (SQ -1) – накопленная частота интервала, предшествующего
интервалу, содержащему нижний квартиль (верхний) квартиль;
fQ (fQ ) – частота интервала, содержащего нижний квартиль (верхний)
квартиль
1
3
1
1
3
3

49.

Децили
Варианты, делящие ранжированный ряд на десять равных частей; они
вычисляются по той же схеме, что и квартили:
1
f S d1 1
d1 X d1 i 10
;
f d1
2
f S d2 1
10
d 2 X d2 i
f d2
и т.д.
Квинтили Значения признака, делящие ряд на пять равных частей. Они вычисляются
по той же схеме, что квартили и децили
Перцентили Значения признака, делящие ряд на 100 равных частей