Похожие презентации:
Средние величины
1. Средние величины
2. Содержание
1. Средняя величина: понятие и виды2. Средняя арифметическая и ее свойства
3. Структурные средние
3.
Средняя величинаобобщающий показатель,
характеризующий типичный уровень
явления, и при этом выражающий
размер признака в расчете на единицу
совокупности
4.
Признаки средней величины:1. Обобщающий, типичный характер
2. Историческая конкретность
3. Объективность
4. Абстрактность
5.
Требования к применению средних:Использование массовых данных при расчете
средней
Однородность совокупности
Дополнение общих средних групповыми
средними
При подборе формы средней необходимо
исходить из экономического смысла
осредняемого показателя
5
6.
Фонд зарплатыСредняя заработная плата
Число работников
Валовой сбор
Средняя урожайность
Посевная площадь
Объем бракованной продукции
Средний % брака
Объем выпущенной продукции
6
7.
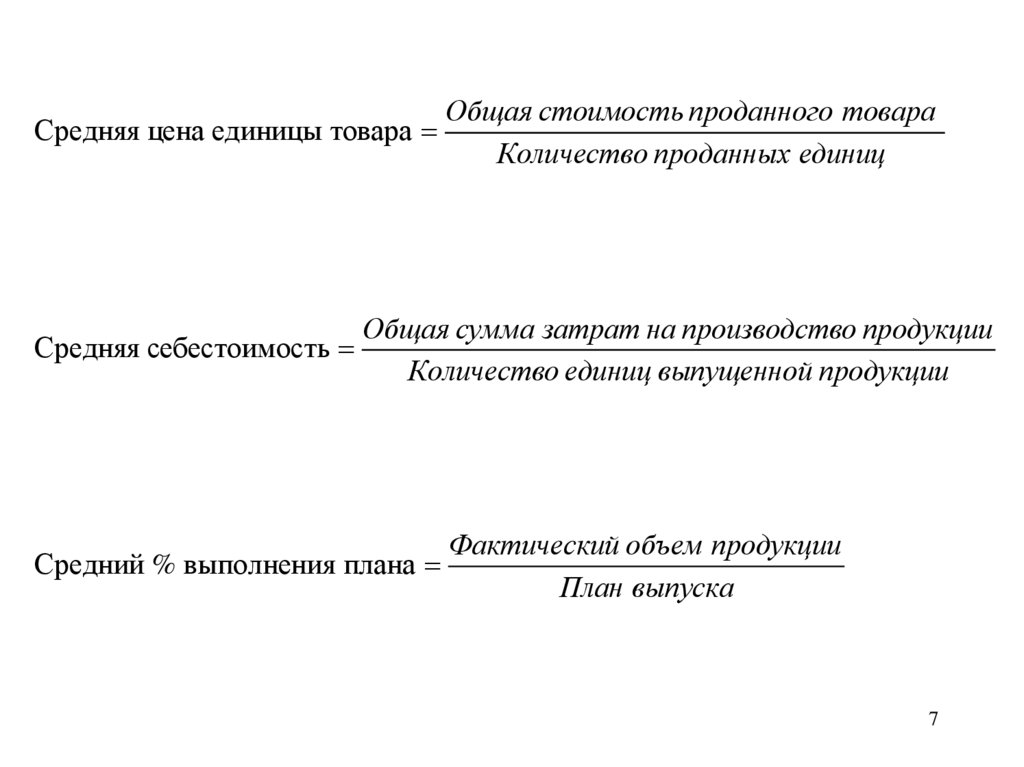
Средняя цена единицы товараСредняя себестоимость
Общая стоимость проданного товара
Количество проданных единиц
Общая сумма затрат на производство продукции
Количество единиц выпущенной продукции
Средний % выполнения плана
Фактический объем продукции
План выпуска
7
8.
ВИДЫ средних величинСтепенные средние:
простые
взвешенные
Структурные средние:
мода
медиана
8
9.
Степенные средниеПростые
Взвешенные
n
x
m
x
i 1
n
m
i
n
x m
x f
m
i
i 1
n
f
i 1
i
хi – значение осредняемого признака
fi – частота, показывающая сколько раз встречаются i-ое
значение осредняемого признака
m – показатель степени средней
n – число вариант
i
10.
Вид степеннойсредней
Гармоническая
Геометрическая
Показатель
степени (m)
-1
0
Формула расчета
Простая
n
х
х
Взвешенная
1
х
i
n
x
i
Хронологическая
Квадратическая
1
-
2
х
х
i
n
М
М
x
i
i
i
n
i 1
Арифметическая
х
х
f
k
fi
x
i
i 1
х f
х
f
i
i
i
1
1
х1 х2 х3 ... хn 1 xn
2
х 2
n 1
х
2
х
i
n
х
2
х
i fi
f
i
11.
Средняя арифметическаяПростая:
Взвешенная:
x
x
n
xf
x
f
11
12.
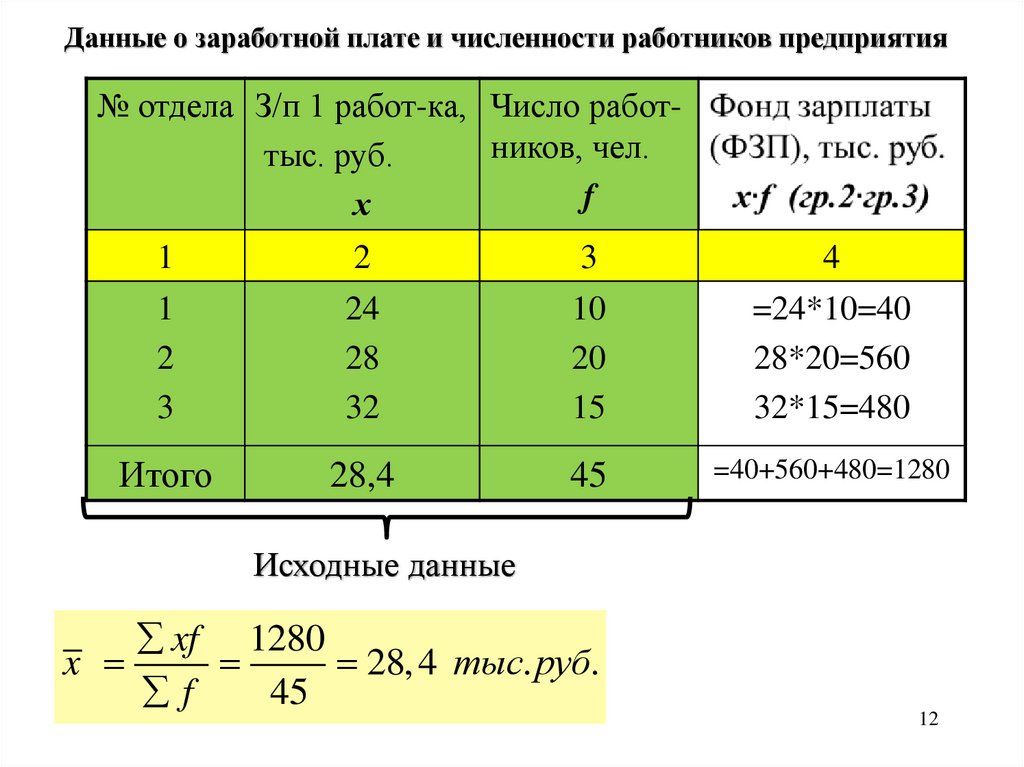
Данные о заработной плате и численности работников предприятия№ отдела З/п 1 работ-ка, Число работников, чел.
тыс. руб.
f
х
1
1
2
3
2
24
28
32
3
10
20
15
4
=24*10=40
28*20=560
32*15=480
Итого
28,4
45
=40+560+480=1280
Исходные данные
xf 1280
x
28, 4 тыс. руб.
f
45
12
13.
xxd f
df
где df – удельный вес в частотах (в общей
численности
единиц совокупности)
13
14.
№ отдела Зарплата1 работника,
тыс. руб.
1
2
3
Итого
x
Уд. вес в числе
работников, %
х
df
24
28
32
-
22
45
33
100
xd f
df
Условный фонд
зарплаты на 100
раб., тыс. руб.
х df
528
1260
1056
2844
2844
28, 4 тыс. руб.
100
14
15.
Средняя гармоническаяПростая:
Взвешенная:
n
x
1
x
xf
x
xf
x
x
15
16.
Данные об оплате труда работников предприятия№ отдела
1
2
3
Итого
Зарплата
1 работника,
тыс. руб.
Фонд зарплаты,
тыс. руб.
Число
работников,
чел.
х
М=х f
М
х
26
29
32
28,9
364
522
384
1270
14
18
12
44
1270
x
28, 9 тыс. руб.
44
x
16
17.
dMx
dM
x
где dМ – удельный вес в определяющем показателе (в
общем объеме значений признака)
17
18.
№ отдела Зарплата1 работника,
тыс. руб.
х
1
2
3
Итого
26
29
32
Уд. вес в фонде Условное число
зарплаты, %
работников на 100
тыс. руб. фонда з/п,
чел.
dM
dM
x
28,7
41,1
30,2
100,0
1,10
1,42
0,94
3,46
dM
100
x
28,9 тыс. руб.
d
3, 46
M
x
18
19.
Средняяхронологическая:
1
1
x1 x2 ... xn 1 xn
2
x 2
n 1
Запасы на начало месяца, тыс.руб.:
1.01
1.02
1.03
1.04
20
24
22
26
1
1
20 24 22 26
69
2
2
Х
23 тыс. руб.
4 1
3
19
20.
Средняя квадратическаяПростая:
x
x
n
x
x f
f
Взвешенная:
2
2
20
21.
Средняя геометрическаяПростая:
Взвешенная:
x n x
x x
n
f
21
22.
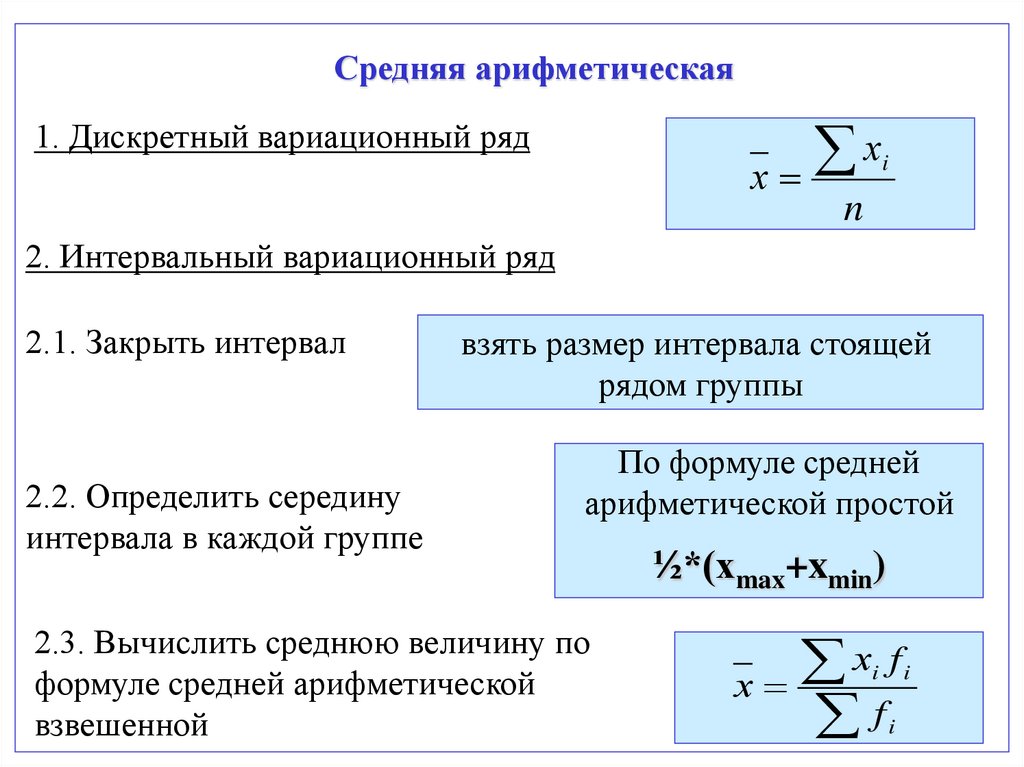
Средняя арифметическаях
х
1. Дискретный вариационный ряд
i
n
2. Интервальный вариационный ряд
2.1. Закрыть интервал
2.2. Определить середину
интервала в каждой группе
взять размер интервала стоящей
рядом группы
По формуле средней
арифметической простой
2.3. Вычислить среднюю величину по
формуле средней арифметической
взвешенной
½*(хmax+xmin)
х f
х
f
i
i
i
23.
Группировка магазинов по размеру торговой площадиГруппы предприятий
Число
по размеру торговой магазинов,
площади, м2
единиц
До 100
3
100 – 120
13
120 – 140
15
140 – 160
20
160 – 180
8
Свыше 180
1
Итого
60
Середина интервала, м2
[100 (120 100)] 100 80 100
90
2
2
100 120
110
2
140 160
150
2
120 140
130
2
160 180
170
2
180 [180 (180 160)] 180 200
190
2
2
-
90 * 3 110 *13 130 *15 150 * 20 170 * 8 190 *1
хар
136,7 м2
60
24.
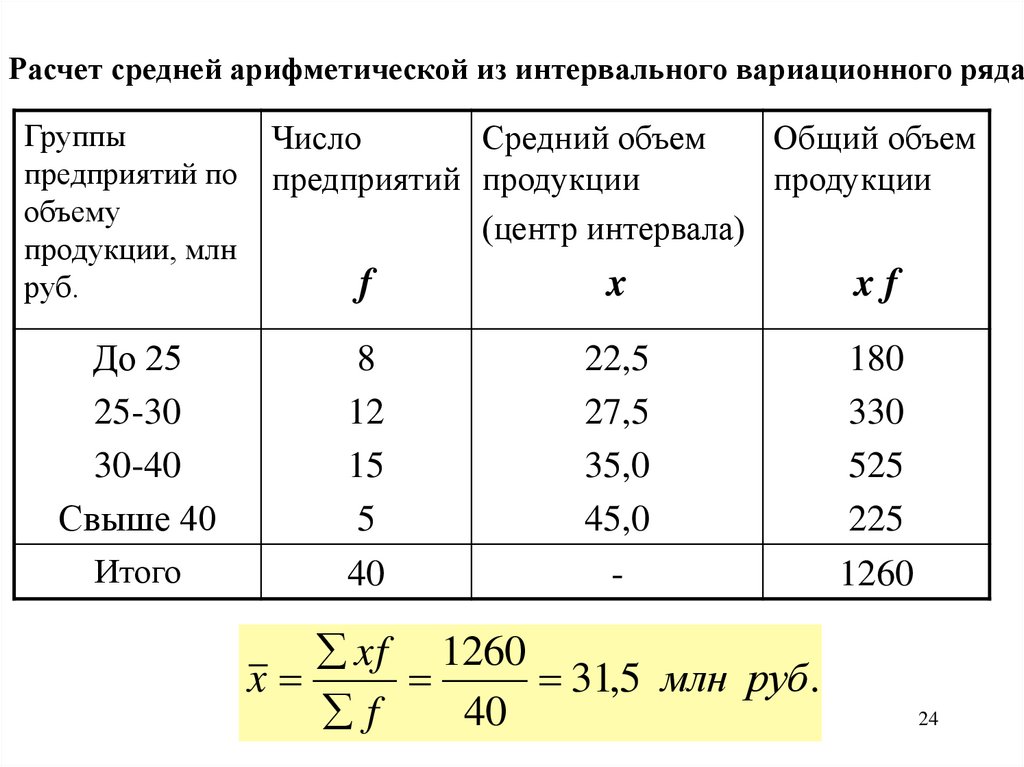
Расчет средней арифметической из интервального вариационного рядаГруппы
предприятий по
объему
продукции, млн
руб.
До 25
25-30
30-40
Свыше 40
Итого
Число
Средний объем
Общий объем
предприятий продукции
продукции
(центр интервала)
f
x
xf
8
12
15
5
40
22,5
27,5
35,0
45,0
-
180
330
525
225
1260
xf 1260
x
31,5 млн руб.
f
40
24
25.
Свойства средней арифметической1. Средняя арифметическая постоянной величины равна этой
постоянной величине.
2. Сумма отклонений вариантов от их средней величины равна
нулю.
3. Если все варианты уменьшить (увеличить) на одно и тоже
число, то средняя арифметическая для этих вариантов также
уменьшиться (увеличиться) на это же число.
4. Если все варианты уменьшить (увеличить) в одно и тоже
число раз, то средняя арифметическая для этих вариантов
также уменьшиться (увеличиться) во столько же раз.
5. Если все веса средней уменьшить (увеличить) в несколько
раз, то средняя арифметическая не изменится.
26.
1. МодаВариант, наиболее часто встречающийся или
имеющий максимальную частоту
Модальным называется интервал с максимальной частотой
f 2 f1
М о х0 i
( f 2 f1 ) ( f 2 f 3 )
где х0 – нижняя граница модального интервала,
i – разность между верхней и нижней границей модального
интервала,
f1 – частота интервала, предшествующая модальному,
f2 – частота модального интервала,
f3 – частота интервала, следующего за модальным.
27.
2. МедианаВариант, стоящий в центре ранжированного
(упорядоченного) ряда
f
М е х0 i
2
S m 1
fm
где х0 – нижняя граница медианного интервала,
i – разность между верхней и нижней границей медианного
интервала,
f – сумма частот интервального ряда,
S(m-1) – сумма накопленных частот в интервалах,
предшествующих медианному,
fm – частота медианного интервала
28.
Группы предприятийпо размеру торговой
площади, м2
До 100
100 – 120
120 – 140
140 – 160
160 – 180
Свыше 180
Итого
Число магазинов,
единиц
Накопленные
частоты
3
13
15
20
8
1
60
3
16
31
51
59
60
-
(20 15)
5
М о 140 20
140 20 145,88 м2
(20 15) (20 8)
17
60
26
4
2
М е 120 20
120 20
125,33 м2
15
15
29.
3. КвартильПорядковые статистики, отсекающие
четверти совокупности (делит ряд на 4
равных части); квартилей – 3.
4. Дециль
Порядковые статистики, отсекающие
десятую часть совокупности (делит ряд на
10 равных части); децилей – 9.

























 Математика
Математика








