Похожие презентации:
Средние величины. Виды средних величин
1. ТЕМА: 5
СРЕДНИЕ ВЕЛИЧИНЫ2.
Средняя величинаэто
обобщающий показатель,
характеризующий уровень или размер
варьирующего признака в расчёте
на единицу однородной совокупности
в конкретных условиях места и времени.
3.
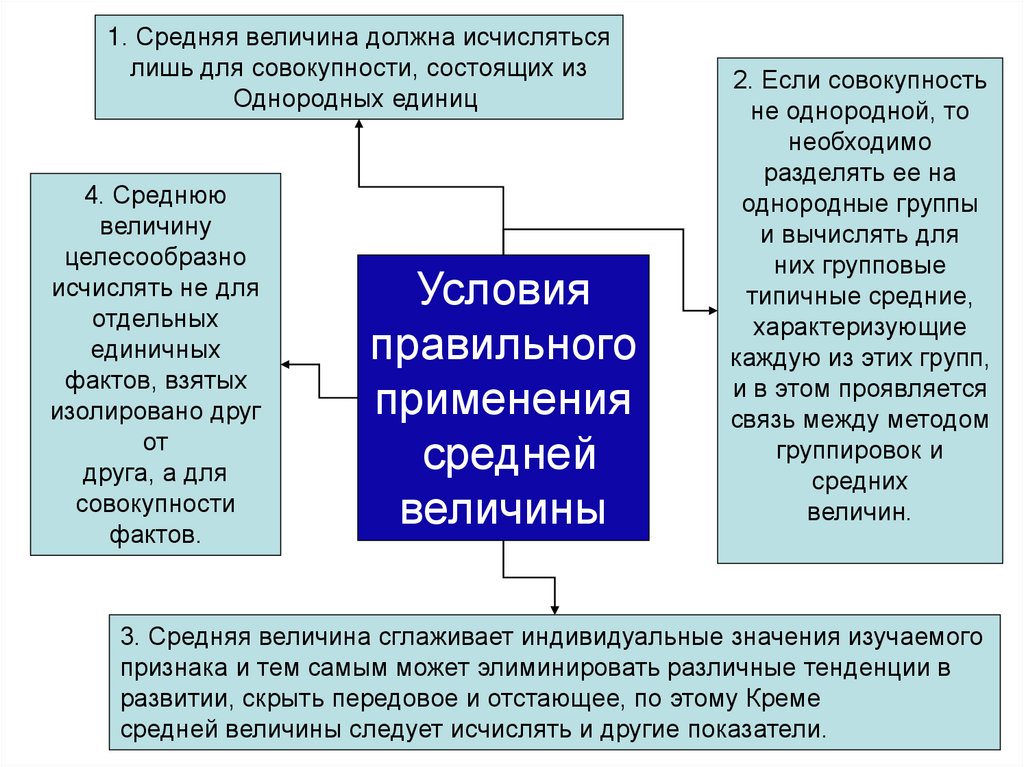
1. Средняя величина должна исчислятьсялишь для совокупности, состоящих из
Однородных единиц
4. Среднюю
величину
целесообразно
исчислять не для
отдельных
единичных
фактов, взятых
изолировано друг
от
друга, а для
совокупности
фактов.
Условия
правильного
применения
средней
величины
2. Если совокупность
не однородной, то
необходимо
разделять ее на
однородные группы
и вычислять для
них групповые
типичные средние,
характеризующие
каждую из этих групп,
и в этом проявляется
связь между методом
группировок и
средних
величин.
3. Средняя величина сглаживает индивидуальные значения изучаемого
признака и тем самым может элиминировать различные тенденции в
развитии, скрыть передовое и отстающее, по этому Креме
средней величины следует исчислять и другие показатели.
4.
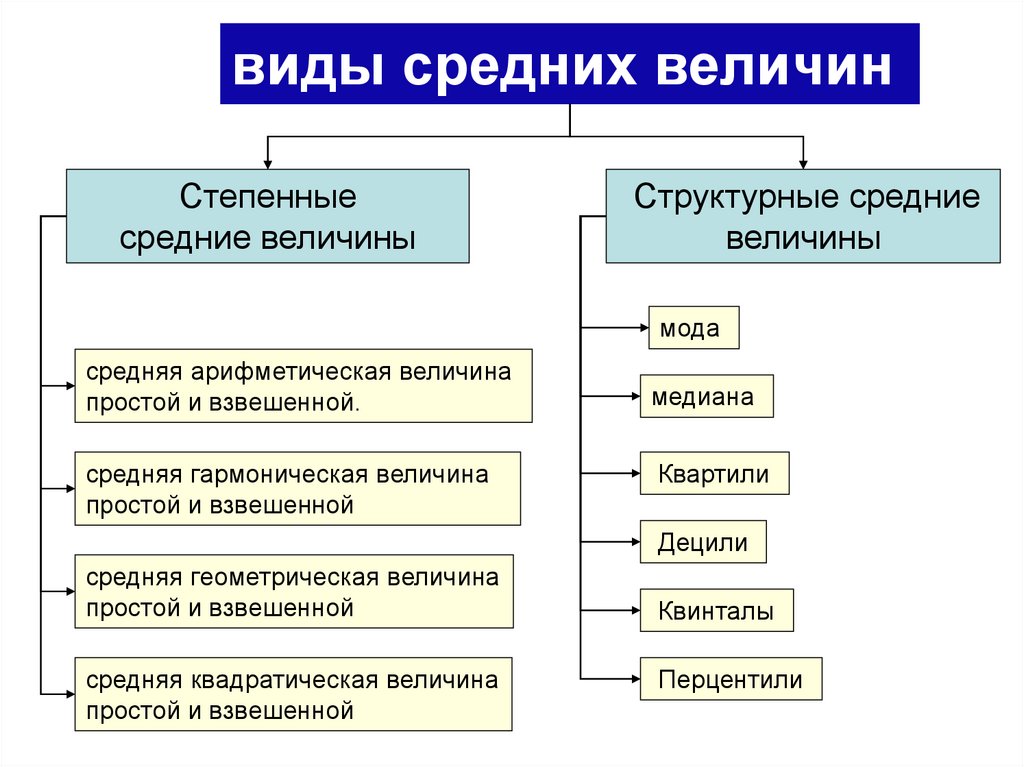
виды средних величинСтепенные
средние величины
Структурные средние
величины
мода
средняя арифметическая величина
простой и взвешенной.
средняя гармоническая величина
простой и взвешенной
медиана
Квартили
Децили
средняя геометрическая величина
простой и взвешенной
средняя квадратическая величина
простой и взвешенной
Квинталы
Перцентили
5.
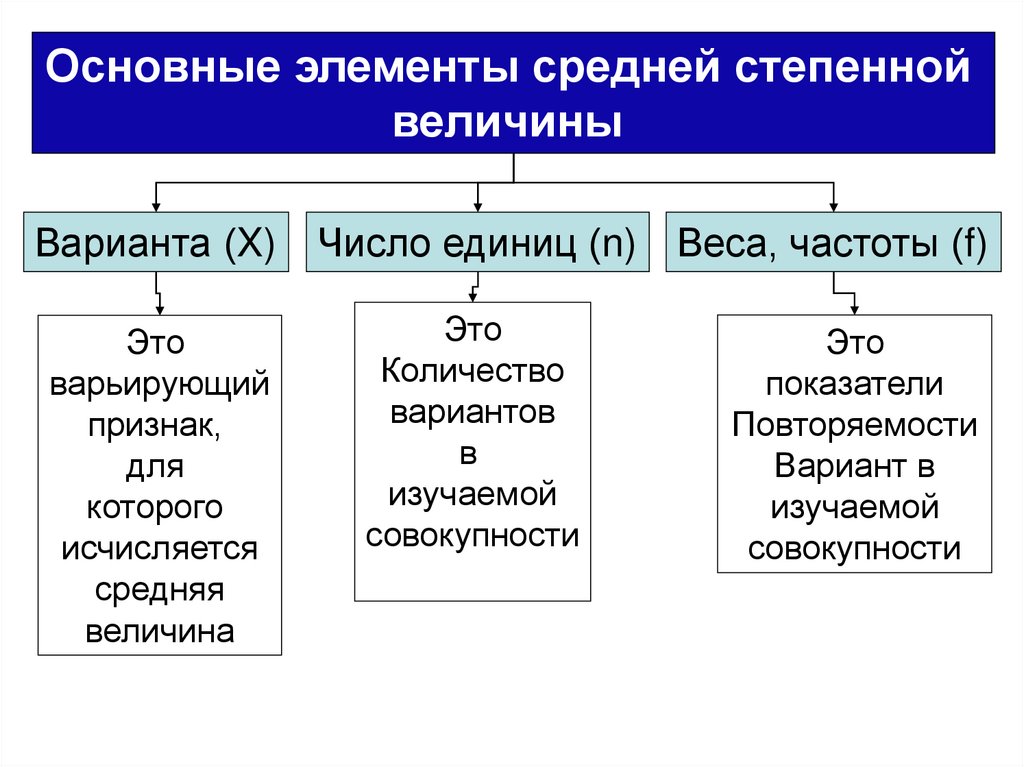
Основные элементы средней степеннойвеличины
Варианта (X)
Это
варьирующий
признак,
для
которого
исчисляется
средняя
величина
Число единиц (n) Веса, частоты (f)
Это
Количество
вариантов
в
изучаемой
совокупности
Это
показатели
Повторяемости
Вариант в
изучаемой
совокупности
6.
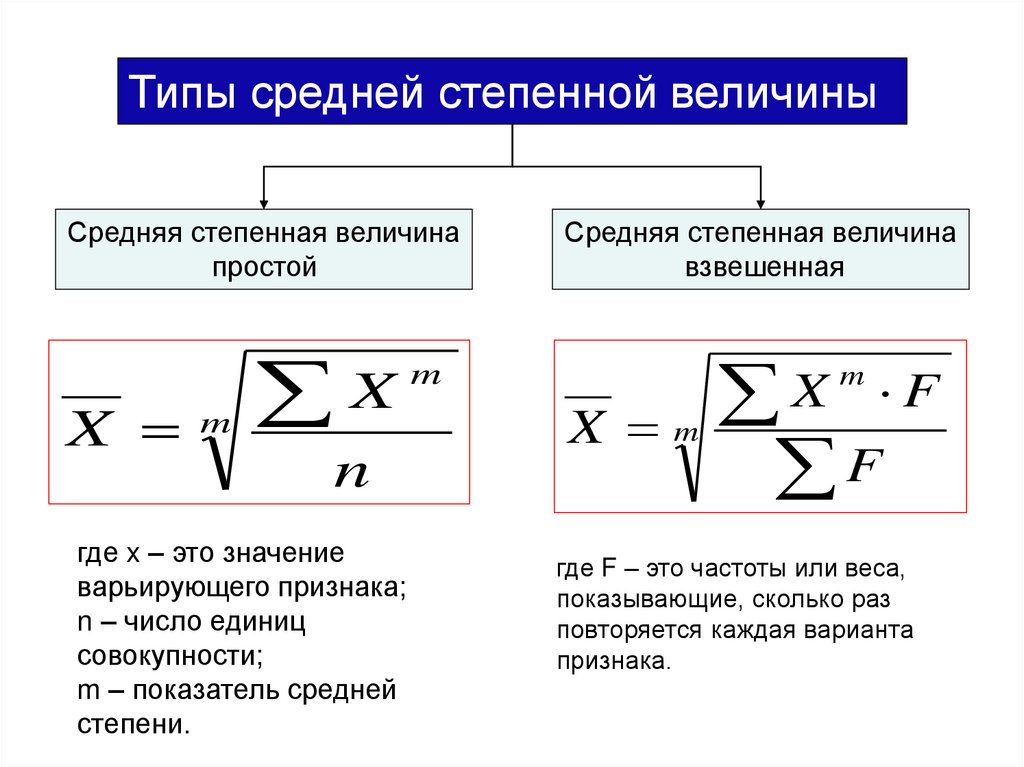
Типы средней степенной величиныСредняя степенная величина
простой
X
m
X
n
где x – это значение
варьирующего признака;
n – число единиц
совокупности;
m – показатель средней
степени.
Средняя степенная величина
взвешенная
m
X F
F
m
X m
где F – это частоты или веса,
показывающие, сколько раз
повторяется каждая варианта
признака.
7.
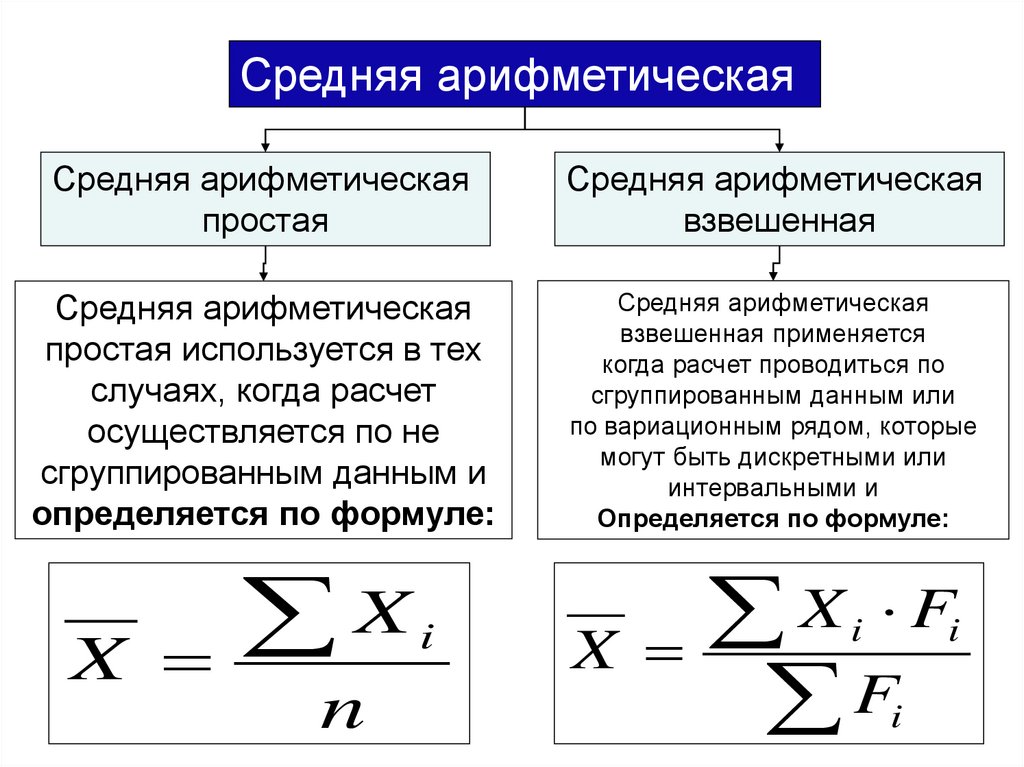
Средняя арифметическаяСредняя арифметическая
простая
Средняя арифметическая
взвешенная
Средняя арифметическая
простая используется в тех
случаях, когда расчет
осуществляется по не
сгруппированным данным и
определяется по формуле:
Средняя арифметическая
взвешенная применяется
когда расчет проводиться по
сгруппированным данным или
по вариационным рядом, которые
могут быть дискретными или
интервальными и
Определяется по формуле:
X
X
n
i
X
X F
F
i
i
i
8.
При наличии вариационногонепрерывного ряда распределения как с
равными так и с неравными
интервалами.
То для вычисления средней
арифметической взвешенной, находится
среднее значение каждого интервала,
как полусуммы его верхней и нижней
границы.
Эти средние значения интервалов
являются новыми значениями
вариантов, подлежащими усреднению.
9.
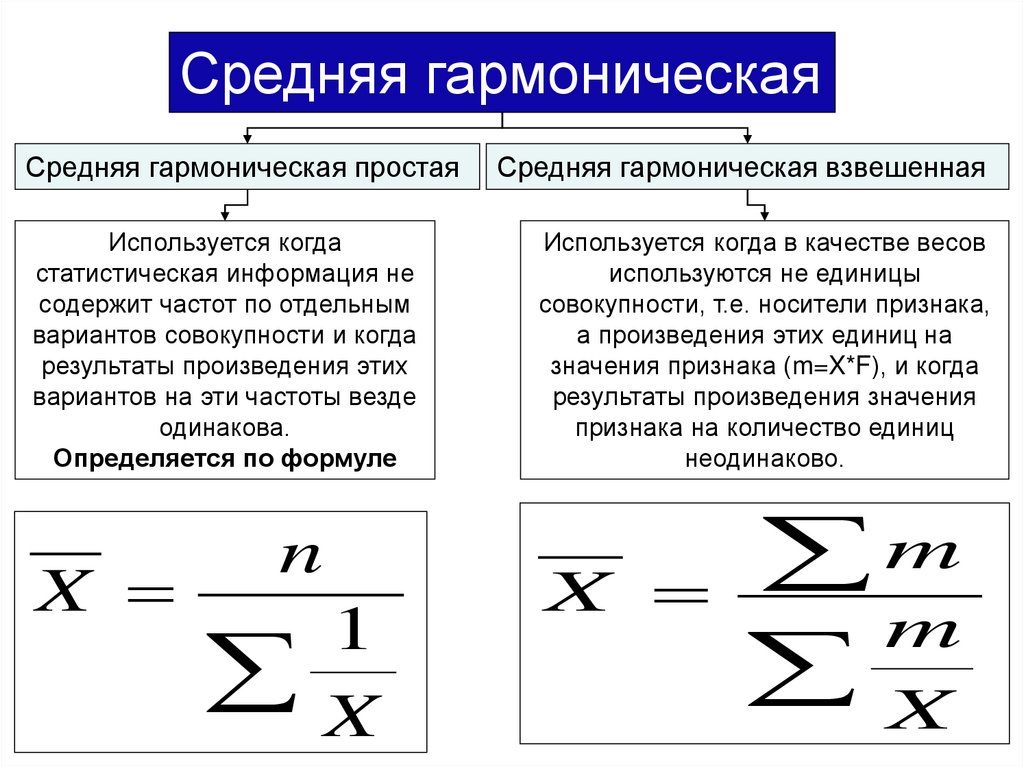
Средняя гармоническаяСредняя гармоническая простая
Используется когда
статистическая информация не
содержит частот по отдельным
вариантов совокупности и когда
результаты произведения этих
вариантов на эти частоты везде
одинакова.
Определяется по формуле
X
n
1
X
Средняя гармоническая взвешенная
Используется когда в качестве весов
используются не единицы
совокупности, т.е. носители признака,
а произведения этих единиц на
значения признака (m=X*F), и когда
результаты произведения значения
признака на количество единиц
неодинаково.
X
m
m
X
10.
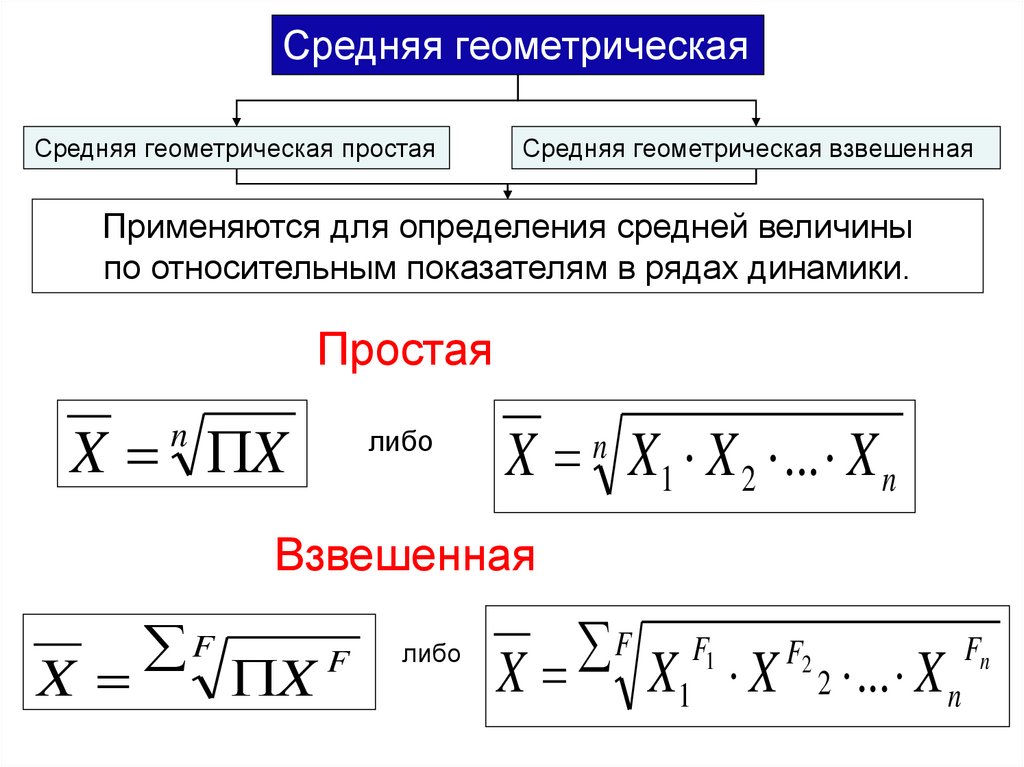
Средняя геометрическаяСредняя геометрическая простая
Средняя геометрическая взвешенная
Применяются для определения средней величины
по относительным показателям в рядах динамики.
Простая
X X
n
либо
X n X1 X 2 ... X n
Взвешенная
X
F
X
F
либо
F
F1
F2
X X X 2 ... X
1
Fn
n
11.
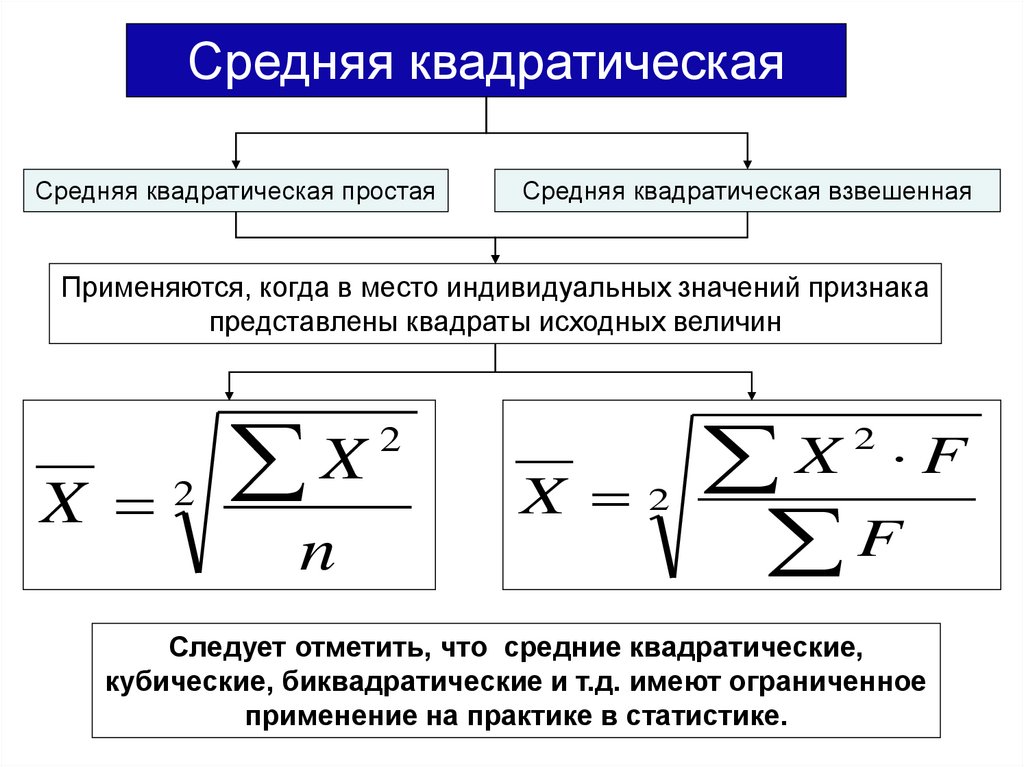
Средняя квадратическаяСредняя квадратическая простая
Средняя квадратическая взвешенная
Применяются, когда в место индивидуальных значений признака
представлены квадраты исходных величин
X 2
X
n
2
X F
F
2
X 2
Следует отметить, что средние квадратические,
кубические, биквадратические и т.д. имеют ограниченное
применение на практике в статистике.
12.
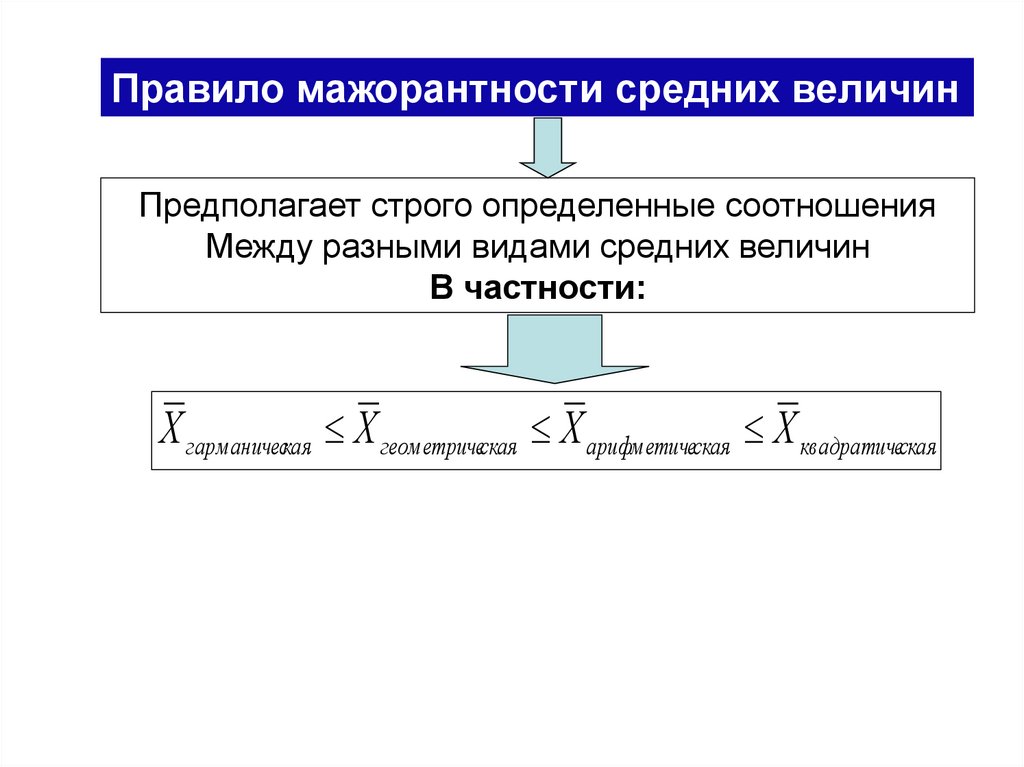
Правило мажорантности средних величинПредполагает строго определенные соотношения
Между разными видами средних величин
В частности:
Х гарманическая Х геометрическая Х арифметическая Х квадратическая
13.
Исчисление средней величины способоммомента первого порядка
Средняя величина способом момента
первого порядка исчисляется при наличии
непрерывного вариационного ряда
распределения с равными интервалами и
определяется по формуле:
X m1 h
А - середина центрального интервала;
h – это ширина интервала;
m1 - это момент первого порядка.
Xi
h Fi
m1
Fi
14.
Средняя структурная величина: МодаЭто
вариант, который чаще всего, встречается в изучаемой совокупности.
В вариационном дискретном ряду модой выступает вариант,
имеющий наибольшую частоту.
В интервальном ряду мода Определяется по формуле:
FМо FМо 1
Mо X 0 h
FМо FМо 1 FМо FМо 1
X 0 - нижняя граница модального интервала;
h – ширина модального интервала;
Fm - частота модального интервала;
Fm 1 - частота интервала, предшествующего модальному интервалу;
Fm 1- частота интервала – следующего за модальные.
15.
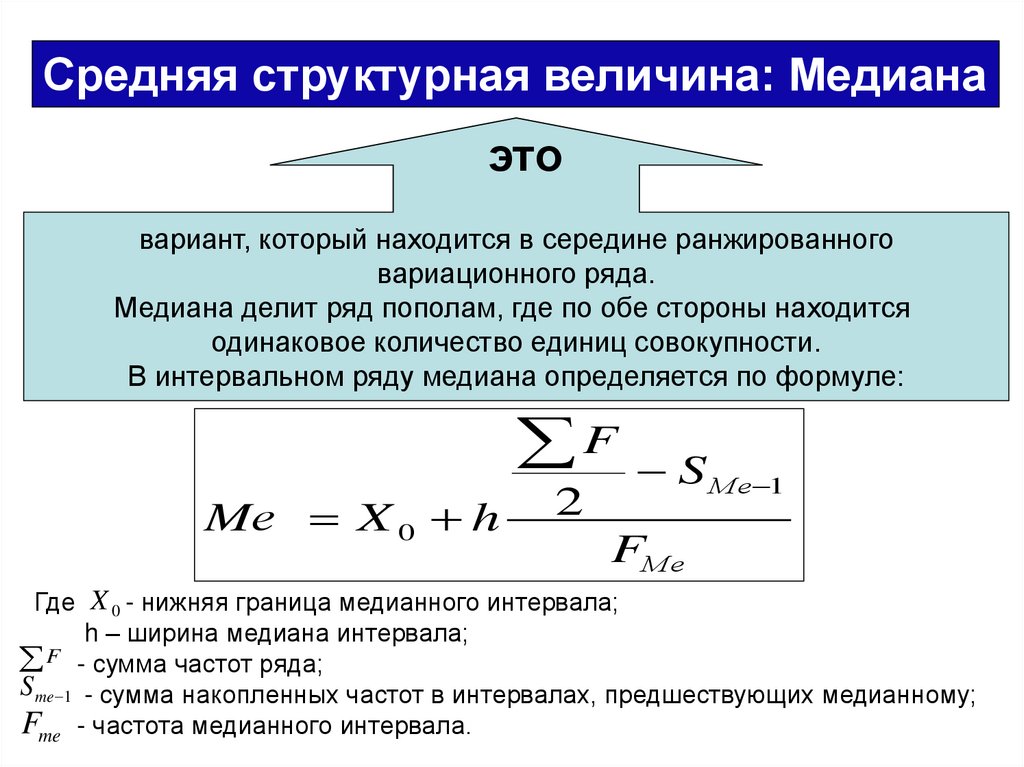
Средняя структурная величина: Медианаэто
вариант, который находится в середине ранжированного
вариационного ряда.
Медиана делит ряд пополам, где по обе стороны находится
одинаковое количество единиц совокупности.
В интервальном ряду медиана определяется по формуле:
F
Mе X 0 h
2
S Ме 1
FМе
Где X 0 - нижняя граница медианного интервала;
h – ширина медиана интервала;
F - сумма частот ряда;
S me 1 - сумма накопленных частот в интервалах, предшествующих медианному;
Fme - частота медианного интервала.
16.
Квартилизначения признака, делящие ранжированную интервальный
ряд на четыре равные части
Нижний квартиль
Нижний квартиль отделяющий ¼
Часть совокупности с наименьшими
Значениями признака.
Q1 xQ1 hQ1
1
F S Q1 1
4
FQ1
Верхний квартиль
Верхний квартиль, отсекающий ¼
Часть с наибольшими значениями
Признака.
Q3 xQ 3 hQ 3
3
F S Q 3 1
4
FQ 3
гдеХ Q1 ( X Q3 ) нижняя граница интервала,
содержащег о нижний (вверхний) квартиль;
SQ1 -1 ( S Q3 1 ) накопленная частота интервала, предшествующего интервалу,
содержащем у нижний квартиль (вверхний) квартиль;
f Q1 ( f Q3 ) частота интервала, содержащег о нижний квартиль (вверхний) квартиль.
17.
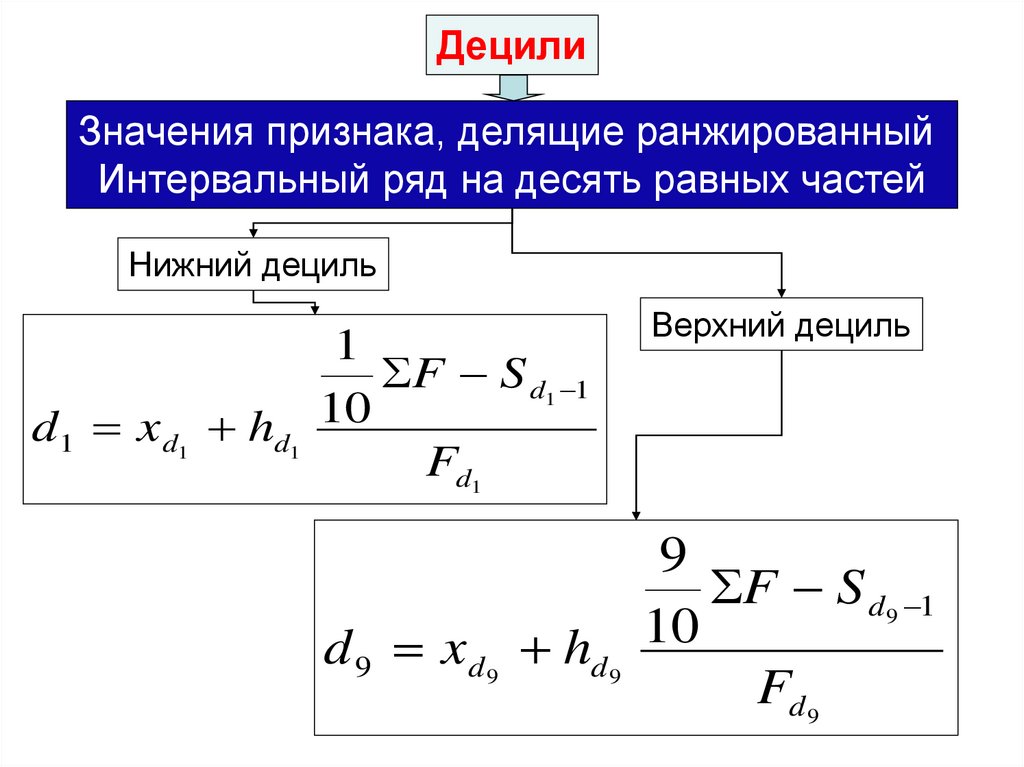
ДецилиЗначения признака, делящие ранжированный
Интервальный ряд на десять равных частей
Нижний дециль
d1 x d1 hd1
1
F S d1 1
10
Fd1
d 9 x d 9 hd 9
Верхний дециль
9
F S d 9 1
10
Fd 9
18.
КвинтилиЗначения признака, делящие интервальный ряд
На пять равных частей.
Квинтили вычисляются по той же схеме, что
квартили и децили.
Перцентили
Значения признака, делящие интервальный
ряд на 100 равных частей.






 Математика
Математика








