Похожие презентации:
Теоретические основы электротехники. Анализ электрических цепей методом контурных токов и методом узловых потенциалов
1. Дисциплина: Теоретические основы электротехники
2. Лекция №1
Лекция №4Тема: «Анализ
электрических цепей
методом контурных
токов и методом
узловых потенциалов»
3. Учебные вопросы
1. Метод контурныхтоков.
2. Метод узловых
потенциалов.
4. Литература
1. Бессонов Л.А.Теоретические основы
электротехники.
Электрические цепи:
учебник для бакалавров. –
М. : Издательство Юрайт,
2012, с. 38-42, с. 53-57.
5.
1. Метод контурных токов1.1. Содержание метода
Метод контурных токов предложен Максвеллом и является
дальнейшим развитием метода непосредственного применения
законов Кирхгофа. Метод предусматривает составление для
ряда независимых контуров заданной цепи системы так
называемых контурных уравнений и ее разрешение
относительно неизвестных контурных токов, входящих в
уравнения.
Контурными токами называются расчетные (фиктивные)
токи, циркулирующие внутри указанных контуров. Условные
положительные направления контурных токов выбираются
произвольно.
Введение контурных токов позволяет уменьшить число
уравнений на количество независимых узлов цепи и составить
расчетные уравнения только на основе второго закона
Кирхгофа.
5
6.
Сопротивления элементов, входящие вкаждое контурное уравнение,
подразделяются на собственные
сопротивления контуров и взаимные
сопротивления общих ветвей смежных
контуров.
По найденным в процессе решения системы
контурных уравнений контурным токам
определяются реальные токи в ветвях.
Универсальная система уравнений для
трёх независимых контуров:
I11R11 – I22R12 – I33R13 = E11
– I11R21 + I22R22 – I33R23 = E22
– I11R31 – I22R32 + I33R33 = E33
6
7.
Универсальная система уравненийдля двух независимых контуров:
I11R11 – I22R12 = E11
– I11R21 + I22R22 = E22
Rnn – собственные сопротивления
контуров; n =1,2,3…….
Собственные сопротивления контуров
определяются сложением всех
сопротивлений, входящих в n - контур
7
8.
Rkn = Rnk – сопротивления смежныхветвей; k = 1,2,3…….
Сопротивления смежных ветвей
определяются сопротивлением ветви,
находящейся на границе контура n и
контура k.
Enn – собственные ЭДС контуров,
которые определяются алгебраическим
суммированием всех источников ЭДС,
входящих в контур n.
8
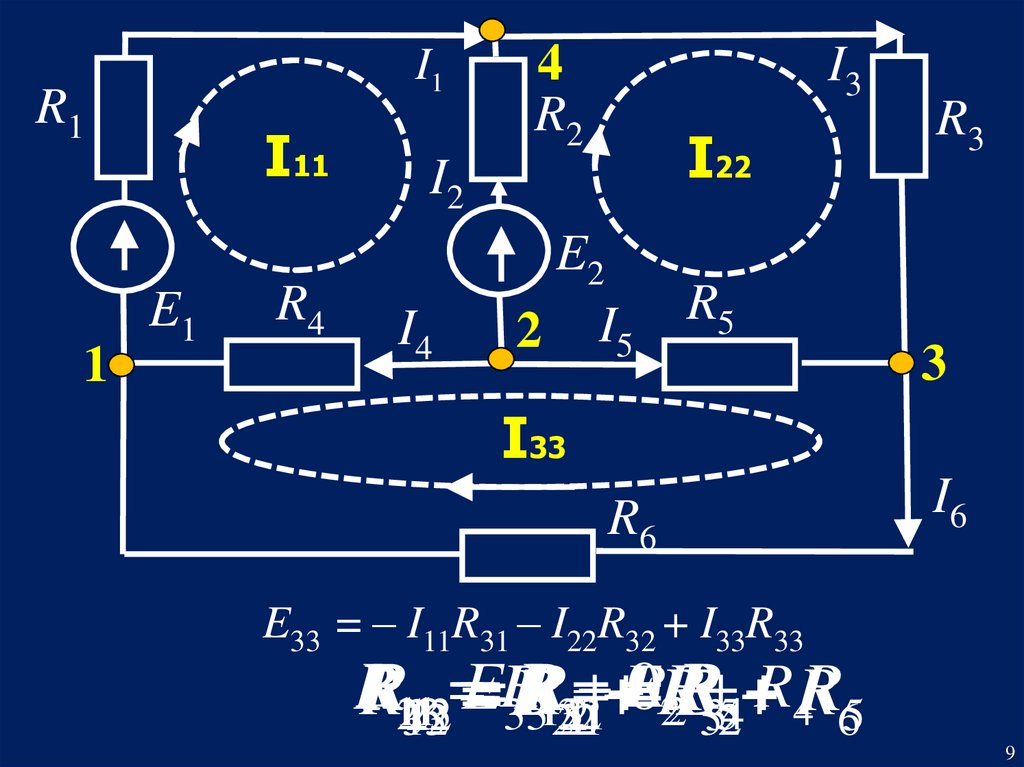
9.
I1R1
1
I11
E1
R4
4
R2
I3
I22
I2
I4
E2
2 I5
R3
R5
3
I33
R6
I6
E3311===––II11I1111
I2222RRR223212–+–II33
I3333RRR233313
EE22
RRR
+––II22
11
21
31
E
=
E
R
–
+
E
R
+
R
R
=
E
R
=
=
0
R
R11
=
R
+
R
+
R
E
E
1
2
2
4
23
13 33 22
32
31
22
33
42
53524
65
12
21
9
10.
В результате решениясформированной системы
уравнений определяются
контурные токи с
последующим переходом к
реальным токам,
протекающим в ветвях
электрической цепи.
10
11.
1.2 Алгоритм расчета методомконтурных токов
1. Составление расчетной схемы замещения
цепи; выбор независимых контуров,
условных положительных направлений
контурных токов и составление системы
контурных уравнений.
2. Решение системы контурных уравнений
относительно неизвестных контурных токов.
3. Определение реальных токов в ветвях (на
основе контурных токов).
4. Проверка правильности решения задачи в
целом.
11
12.
2. Метод узловых потенциалов2.1. Содержание метода
Метод узловых напряжений (потенциалов) также
предложен Максвеллом; его разработка была
связана со стремлением уменьшить число
уравнений при расчете сложной цепи.
Метод узловых потенциалов основан на первом
законе Кирхгофа и законе Ома и
предусматривает составление для заданной
цепи, имеющей q узлов, системы так называемых
узловых уравнений, состоящей из q-1 уравнения,
и ее разрешение относительно неизвестных
узловых напряжений, зная которые можно найти
токи в цепи.
12
13.
Содержание метода узловых потенциалов(продолжение)
В данном методе потенциал одного из узлов цепи,
называемый опорным узлом, принимается равным
нулю.
Под узловыми напряжениями понимают
напряжения остальных узлов цепи относительно
опорного узла .
Проводимости элементов, входящие в каждое
узловое уравнение, подразделяются на собственные
проводимости узлов, взаимные проводимости
смежных узлов и проводимости ветвей.
В узловых уравнениях суммы членов являются
алгебраическими. Перед произведением ставится
знак "плюс", если ЭДС направлена к узлу , для
которого составляется уравнение, и знак "минус",
если ЭДС направлена от узла.
13
14.
Универсальнаясистема уравнений для
трёх независимых узлов:
φ1 G11 – φ2 G12 – φ3 G13 = J1
– φ1 G21 + φ2 G22 – φ3 G23 = J2
– φ1 G31 – φ2 G32 + φ3 G33 = J3
14
15.
Универсальнаясистема уравнений для
двух независимых
узлов:
φ1 G11 – φ2 G12 = J1
– φ1 G21 + φ2 G22 = J2
15
16.
Универсальное уравнение дляодного независимого узла
Это частный случай метода
узловых потенциалов, который
называется «метод двух узлов»
16
17.
Gnn – собственные проводимости узлов;n =1,2,3…….
Собственные проводимости узлов
определяются сложением
проводимостей всех ветвей, входящих
в n - узел
Gkn = Gnk – проводимости смежных
узлов; k = 1,2,3…….
Проводимости смежных узлов
определяются
проводимостью
ветви, соединяющей узлы n и k.
17
18.
Jn – собственные узловые токи,которые определяются алгебраическим
суммированием произведений
источников ЭДС Е ветвей на
проводимости ветвей, входящих в узел n,
т.е. Σ Es Gs , где s соответствует номеру
ветви, входящей в узел n.
Если источник ЭДС ветви направлен
к узлу, то произведение Es Gs входит
со знаком «+»,в противном случае —
со знаком «–».
18
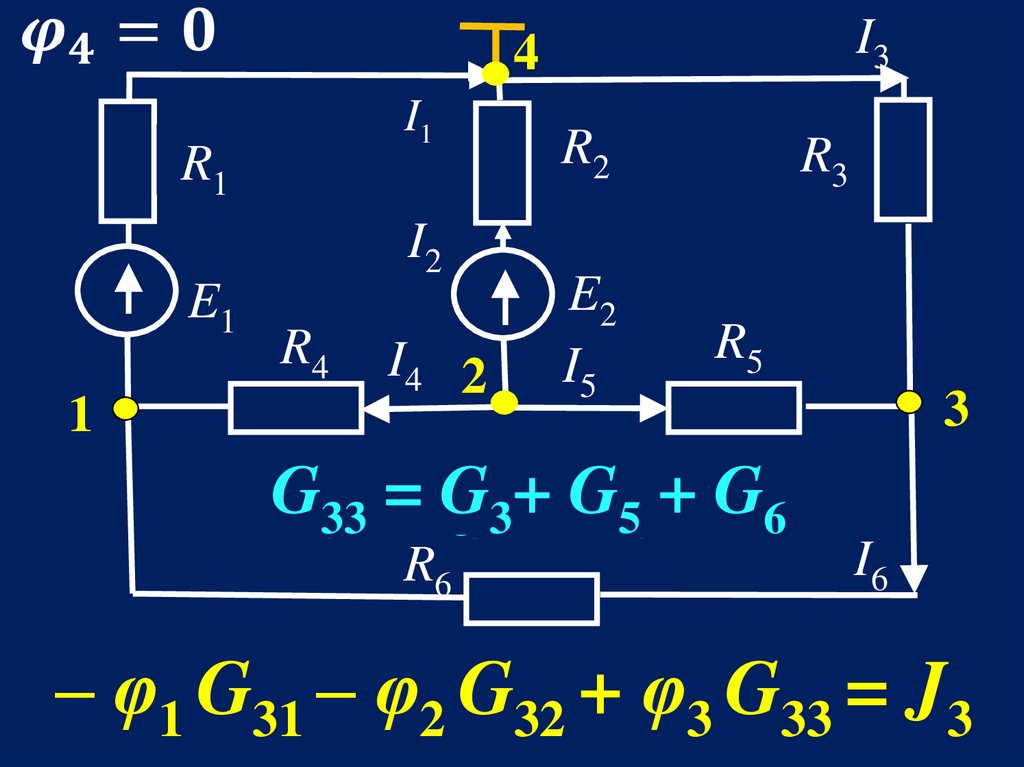
19.
I34
I1
R1
I2
E1
1
R4
I4 2
R2
E2
I5
R3
R5
G
=
G
+
G
+
G
=
G
+
G
+
G
G
=
G
=
G
J
+
=
G
0
+
G
G
=
G
=
J12
–
E
J1G
=
–22
E
G
G
=
G
=
G
33
3
5
11
1
4
6
1
1
322 42 465
321
231
56
223
13
R6
3
I6
–
φ
G
–
φ
G
=
J
– φφ11 G
+
φ
G
–
φ
G
=
G11
–
+
J
2
12
3
13
123
21
2 22
33 23
31
32
33
19
20.
В результате решениясформированной системы
уравнений определяются
потенциалы узлов
электрической цепи, с
последующим переходом к
реальным токам при
помощи закона Ома.
20
21.
2.2 Алгоритм расчета методомузловых потенциалов
1. Составление расчетной схемы замещения
цепи; выбор условных положительных
направлений токов в ветвях и опорного узла.
2. Составление системы узловых уравнений и
решение этой системы относительно узловых
потенциалов.
3. Определение токов в ветвях на основе
закона Ома с учетом найденных узловых
потенциалов.
4. Проверка правильности решения задачи в
целом.
21
22.
Спасибо завнимание!
22













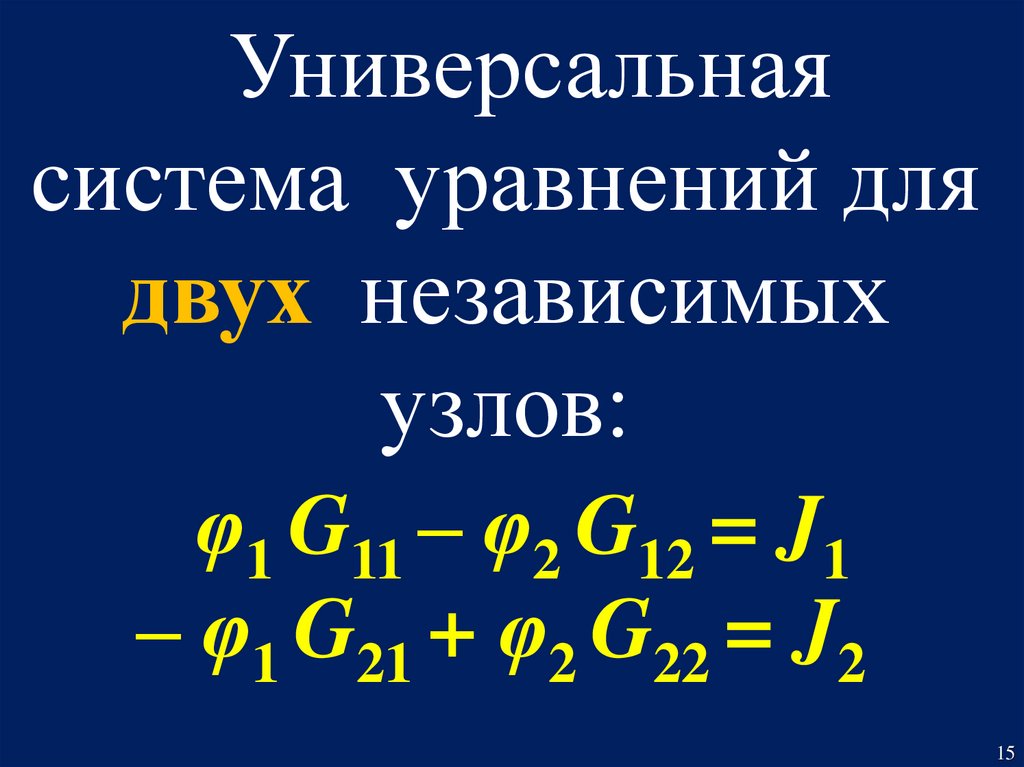






 Физика
Физика








