Похожие презентации:
Электротехника и электроника. Методы расчета сложных линейных цепей постоянного тока. (Лекция 2)
1.
Кубанский государственный технологический университетИнститут информационных технологий и безопасности
Кафедра компьютерных технологий и информационной
безопасности
Учебная дисциплина
Электротехника и электроника
Лекция № 2
Методы расчета сложных
линейных цепей постоянного тока
2.
Учебные вопросы:1. Принцип и метод наложения (суперпозиции)
2. Метод контурных токов
3. Метод узловых потенциалов.
4. Метод эквивалентного генератора
Литература:
Литература
1. Зевеке Г.В., Ионкин А.В., Страков С.В. Основы теории цепей: Учебник для
вузов, - М.: Энергоатомиздат, 1999 г, с. 21 –32.
2. Бакалов В.П., Игнатов А.Н., Крук Б.И. Основы теории электрических
цепей и электроники: Учебник для вузов, - М.: Радио и связь, 1999 г, с. 24 –34.
3. Касаткин А.С., Немцов М.В. Электротехника: Учебник для вузов, - М.:
Высшая школа, 2003 г, с. 21 –31.
3.
1. Принцип и метод наложения (суперпозиции)воздействие
Х(t)= хк(t)
Электрическая
цепь
реакция
Y(t)= yк(t)
Если рассматривать напряжения и токи источников как задающие
воздействия, а напряжения и токи в отдельных ветвях цепи как
реакцию (отклик) на эти воздействия, то принцип наложения
может быть сформулирован так: реакция линейной
электрической цепи на сумму воздействий равна сумме
реакций от каждого воздействия в отдельности.
Метод наложения (суперпозиции) используется для нахождения
реакции в линейной цепи, находящейся как под воздействием
нескольких источников электрической энергии, так и при сложном
произвольном воздействии одного источника.
I
n
I
k 1
n
k
n – общее число источников
U U k
k 1
4.
Методика анализа ЭЦ методом наложения1. Произвольно выбрать направления всех токов в ветвях исходной
схемы и пронумеровать все независимые источники целыми
числами 1,2 … n;
2. Положить равными нулю все источники ЭДС, кроме первого. При
этом все независимые источники, ЭДС которых равна нулю,
заменить короткозамкнутыми отрезками, а независимые источники
тока – отключить (заменить разрывом цепи). Если независимые
источники имеют внутренние сопротивления, то эти сопротивления
должны остаться на своих местах в схеме.
3. В полученной схеме с одним независимым источником любым
методом, например «методом эквивалентного преобразования
схем» рассчитать все частичные токи Ik1;
4. Аналогичным образом рассчитать все частичные токи Ik2 только от
второго источника (все остальные источники положить равными
нулю). Затем только от третьего Ik3 и так далее до Ikn;
5. Вычислить истинные токи во всех ветвях исходной электрической
схемы как алгебраическую сумму всех частных токов
Частный ток берется со знаком «плюс», если
1
2
n
он совпадает по направлению с истинным
k
k
k
k током, и «минус», если не совпадает.
I I I ... I
5.
Применение метода наложения для анализа и расчета электрической цепиR1
R2
I2
I1
R01
R02
I 3=
R3
E1
E2
Дано: R1= 17 Ом, R01= 3 Ом,
R2= 9 Ом, R02 = 1 Ом, R3= 40 Ом,
Е1= 35 В, Е2= 70 В
Необходимо найти:
найти ток I3
Решение:
I3 = I3(1) + I3(2)
Найдем частые реакции I3(1)
и I3(2)
При закороченном источнике Е2
I
(1)
3
I
I1(1)
(1)
1
( R 2 R02 )
( R 2 R02 R3)
Е1
( R 2 R02 ) R3
R1 R01
R 2 R02 R3
Результат расчета: I = 0,25 А,
I1(1) = 1,25А
(1)
3
R1
где
R2
I1(1)
R01
E1
I2(1)
I =
(1)
3
R3
R02
E2
6.
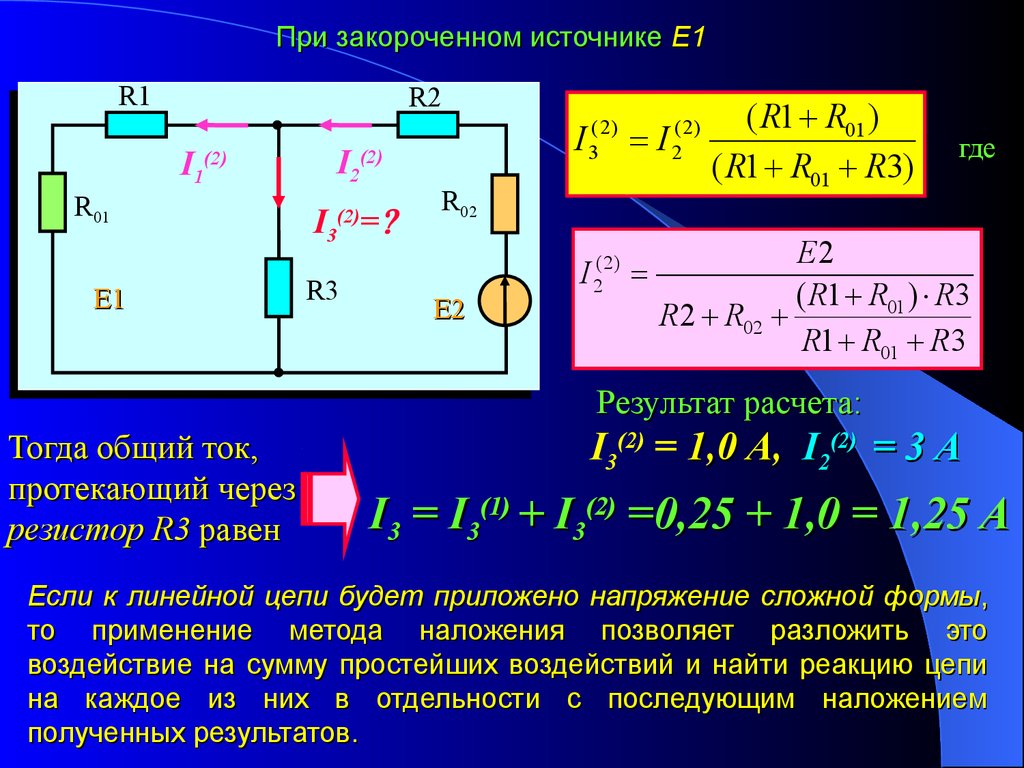
При закороченном источнике Е1R1
R2
I1
(2)
R01
E1
I2
I3 =
(2)
R3
I
(2)
( 2)
3
I
R02
E2
I 2( 2)
( 2)
2
( R1 R01 )
( R1 R01 R3)
где
Е2
( R1 R01 ) R3
R 2 R02
R1 R01 R3
Результат расчета:
Тогда общий ток,
протекающий через
резистор R3 равен
I3(2) = 1,0 А, I2(2) = 3 А
I3 = I3(1) + I3(2) =0,25 + 1,0 = 1,25 А
Если к линейной цепи будет приложено напряжение сложной формы ,
то применение метода наложения позволяет разложить это
воздействие на сумму простейших воздействий и найти реакцию цепи
на каждое из них в отдельности с последующим наложением
полученных результатов.
7.
2. Метод контурных токовМетод контурных токов позволяет снизить число решаемых уравнений до
числа независимых контуров. В его основе лежит введение в каждый
контур условного контурного тока JKI , которое обычно выбирают
совпадающим с направлением обхода контура. При этом для контурного
тока будут справедливы ЗТК и ЗНК.
Методика анализа ЭЦ методом контурных токов
1. Произвольно выбрать направления всех токов в ветвях
исходной схемы; Выбрать K = MУР = NВ – NУЗ + 1- NИТ –
независимых контуров. Обозначить контурные токи Jki так,
чтобы каждый из них проходил через один источник
тока, а оставшиеся выбирают проходящими по ветвям,
не содержащим источников тока.
2. Обходя каждый контур из независимых контуров в
выбранном направлении, записать уравнения по
второму закону Кирхгофа (соблюдая правило знаков)
и решить их относительно контурных токов
8.
mR11 J K 1 R12 J K 2 ... R1K J KK J 0 n Rn E11
n 1
m
RK 1 J K 1 RK 2 J K 2 ... RKK J KK J 0 n Rn EKK
n 1
Rnn – сумма сопротивлений всех ветвей контура n, т.е. собственное
сопротивление контура n; Rns – общее сопротивление контура n и
s , записывается со знаком «плюс», если контурный ток Inn
совпадает по направлению с контурным током Iss, если нет – со
знаком «минус». Еnn – алгебраическая сумма ЭДС контура nn.
ЭДС записывается со знаком «плюс», если контурный ток Inn
совпадает по направлению с направлением ЭДС, иначе со знаком
«минус».
3. Вычислить истинные токи во всех ветвях, используя
первый закон Кирхгофа, как алгебраическую сумму
контурных токов, протекающих по данной ветви
9.
R1R2
I2
I1
R01
JК1
E1
I 3=
R3
1. Введем контурные токи JK1 и JK2
(направление по часовой стрелке).
R02
2. Запишем уравнения по второму
закону Кирхгофа
JК2
( R1 R01 R3 ) J K 1 R3 J K 2 E1
E2
60 J K 1 40 J K 2 35
40 J K 1 50 J K 2 70
R3 J K 1 ( R2 R02 R3 ) J K 2 E 2
Определители системы:
R
Контурные токи
60
40
40
50
60 50 ( 40) ( 40) 1400
35 40
J K 1 1050
35 50 ( 70) ( 40) 1050
J K1
0,75 A
J K1
70 50
R
1400
JK2
J K 2 2800
2,0 A J
R
1400
K2
60
35
40 70
I 3 I K 1 I K 2 0,75 ( 2,0) 1,25 A
60 ( 70) (35) ( 40) 2800
I1 I K 1 0,75 A
I 2 I K 2 2,0 A
10.
3. Метод узловых потенциаловМетод узловых потенциалов является наиболее общим и широко применяется
для расчета электрических цепей, в частности в различных программах
автоматизированного проектирования электронных схем.
Метод узловых потенциалов базируется на первом законе Кирхгофа
и обобщенном законе Ома. Он позволяет снизить число решаемых
уравнений до величины NУР = NУЗ – 1 - NИТ .
В основе этого метода лежит расчет напряжений в (NУЗ – 1 - NИТ) – м
узле электрической цепи относительно базисного узла. После этого
на основании закона Ома находятся токи токи или напряжения на
соответствующих ветвях.
Методика анализа ЭЦ методом узловых
потенциалов (узловых напряжений)
1. Произвольно выбрать направления всех токов в ветвях
исходной схемы;
2. Положить равным нулю потенциал какого-либо узла ЭЦ;
Определить количество уравнений NУР = NУЗ - NИТ –1, NИТ –
число ветвей, содержащих только идеальные источники тока.
11.
3. Решить систему уравнений относительно потенциалов узлов;m
l
n 1
k 1
G11 U У 1 G12 U У 2 ... G1K U УK En Gn J 0 k
m
l
n 1
k 1
GK 1 U У 1 GK 2 U У 2 ... GKK U УK Еn Gn J 0 k
где GSS - алгебраическая сумма проводимостей ветвей, присоединенных к
узлу S, не содержащих источники тока;
GSQ - алгебраическая сумма проводимостей ветвей, непосредственно
соединяющих узел S с узлом Q;
ЕSGS - алгебраическая сумма произведений ЭДС ветвей, примыкающих
к узлу S, на их проводимости; Это произведение берется со знаком «плюс»,
если ЭДС направлена к узлу S, в противном случае – «минус»;
J0S - алгебраическая сумма источников тока, присоединенных к к узлу S.
Ток J берется со знаком «плюс», если он направлен к узлу S, иначе «минус»
4. Вычислить необходимые токи из обобщенного закона Ома
или первого закона Кирхгофа.
12.
R1«1»
R01
E1
U1
I 3 I1 I 2
I2
I1
На основании первого закона
Кирхгофа применительно к узлу 1:
R2
R02
I3=
R3
U1 E1 U1 E 2 U1
R3 R1 R01 R 2 R02
E2
U1
U1
U1
E1
E2
R3 R1 R01 R 2 R02 R1 R01 R 2 R02
«0»
Базисный узел
Уравнение для узлового напряжения U1
1
1
1
G
G
G3
10
20
R1 R01
R 2 R02
R3
U1 (G10 G20 G3 ) E1 G10 E 2 G20
Результаты расчета:
I3
U1 50
1,25 A
R3 40
U1
I1
E1 G10 E 2 G20
U1
G10 G20 G3
35 0,05 70 0,1 1,75 7 8,75
50 B
0,05 0,1 0,025
0,175
0,175
E1 U1
0,75 A
R1 R01
E 2 U1
I2
2,0 A
R 2 R02
13.
4. Метод эквивалентного генератораМетод эквивалентного генератора используется в случае, когда необходимо
найти ток, напряжение или мощность в одной ветви электрической цепи.
При таком подходе остальная часть электрической цепи к которой
подключена данная ветвь рассматривается в виде двухполюсника с
определенными параметрами.
ЭЦ
I
R
R0 = RЭ
E = UXX
Электрическая цепь
I
R
Зажимыцепи
цепи
Зажимы
Метод эквивалентного источника напряжения (теорема Тевенина):
Ток
Тевенина
в любой ветви линейной электрической цепи не изменится, если активный
двухполюсник, к которому подключена данная ветвь, заменить эквивалентным
источником (генератором) напряжения с задающим напряжением, равным
напряжению холостого хода на зажимах разомкнутой ветви, и внутренним
сопротивлением, равным эквивалентному входному сопротивлению
пассивного двухполюсника со стороны разомкнутой ветви.
14.
R1R2
I2
I1
R01
I3=
R3
E1
R02
E2
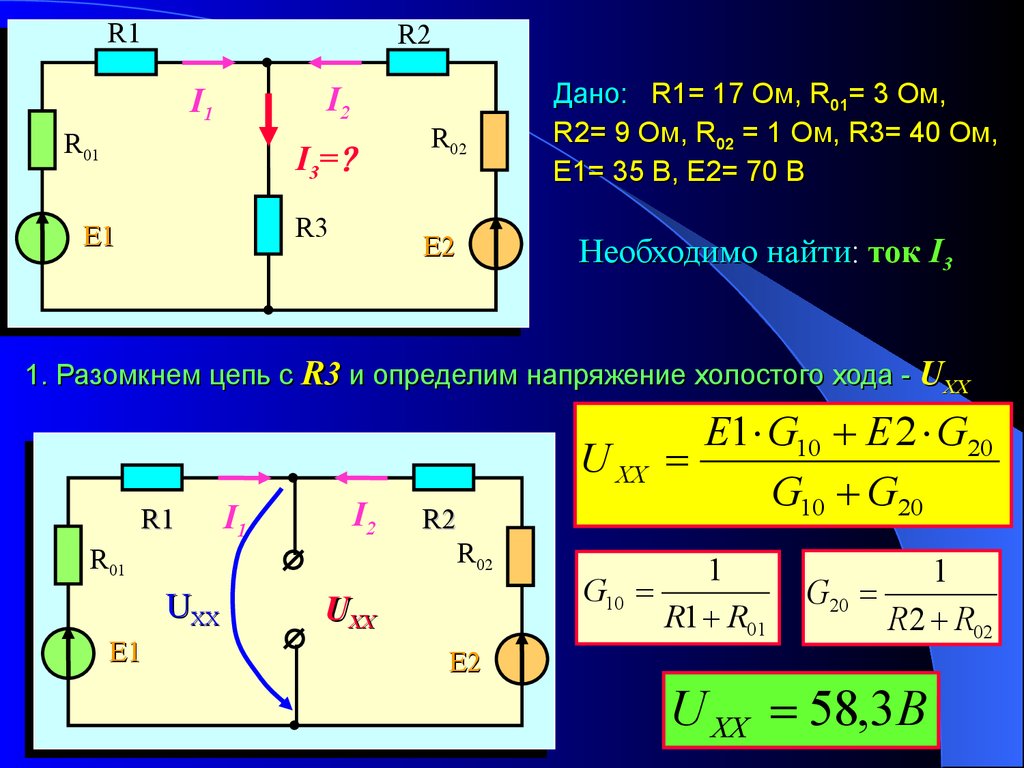
Дано: R1= 17 Ом, R01= 3 Ом,
R2= 9 Ом, R02 = 1 Ом, R3= 40 Ом,
Е1= 35 В, Е2= 70 В
Необходимо найти:
найти ток I3
1. Разомкнем цепь с R3 и определим напряжение холостого хода - UXX
U XX
R1
I1
I2
R01
UХХ
E1
R2
R02
UXX
E2
E1 G10 E 2 G20
G10 G20
1
G10
R1 R01
1
G20
R 2 R02
U XX 58,3B
15.
2. Определим эквивалентное сопротивление RЭ(источники ЭДС заменяются короткозамкнутыми отрезками, а
источники тока – разрывом цепи)
R1
R2
R02
R01
RЭ
E1= 0
E2 = 0
( R1 R01 ) ( R 2 R02 )
RЭ
R1 R01 R 2 R02
20 10 200
RЭ
6,66Ом
20 10 30
Эквивалентная схема для расчета ЭЦ имеет вид
U XX
I3
RЭ R3
I
3
R0 = R Э
E = UXX
58,3
R3
I3
6,66 40
1,25 A
16.
Задание на самостоятельную работуЛитература:
Литература
1. Зевеке Г.В., Ионкин А.В., Страков С.В. Основы теории
цепей: Учебник для вузов, - М.: Энергоатомиздат, 1999 г,
с. 21 –32.
2. Бакалов В.П., Игнатов А.Н., Крук Б.И. Основы теории
электрических цепей и электроники: Учебник для вузов,
- М.: Радио и связь, 1999 г, с. 24 –34.
3. Касаткин А.С., Немцов М.В. Электротехника: Учебник
для вузов, - М.: Высшая школа, 2003 г, с. 21 –31.














 Физика
Физика Электроника
Электроника








