Построение графиков функций с помощью сдвигов и деформаций

1.

Электронное пособие.
Построение графиков функций с
помощью сдвигов и деформаций.

2.

Содержание:
1. Вступление.
2. График функции
y f ( x a) .
3. График функции y f ( x) b .
4. График функции
y mf (x) .
5. График функции
y f (kx) .
6. Композиция сдвигов и деформаций (график сложной функции).
7. Применение метода сдвигов и деформаций при построении
графиков тригонометрических функций.
8. Построение графиков функций, содержащих знак модуля:
а) график функции у = f(|x|);
б) график функции у = |f(x)|;
в) график функции у = |f(|x|)|;
9. Упражнения.
10. Задача – исследование.
11. Тест.
12. Основные результаты.

3.

Дорогие ребята!
Изучая курс алгебры в основной школе, Вы научились, исходя из графика
у f (x) , строить графики следующих функций:
1) у f ( x a )
2) у f ( x) b
3) у f ( x a ) b
4) у mf ( x)
5) у f (kx)
Венцом всех этих преобразований является график функции:
у mf (kx a) b
Кроме этого, Вы научитесь строить графики функций, содержащих знак
модуля, которые обычно вызывают затруднения. Это функции трех видов:
y f (| x |)
y | f ( x) |
y | f (| x |) |
В дальнейшем Вы рассмотрите поэтапное построение графиков всех этих
функций и примените полученные знания при выполнении упражнений.

4.

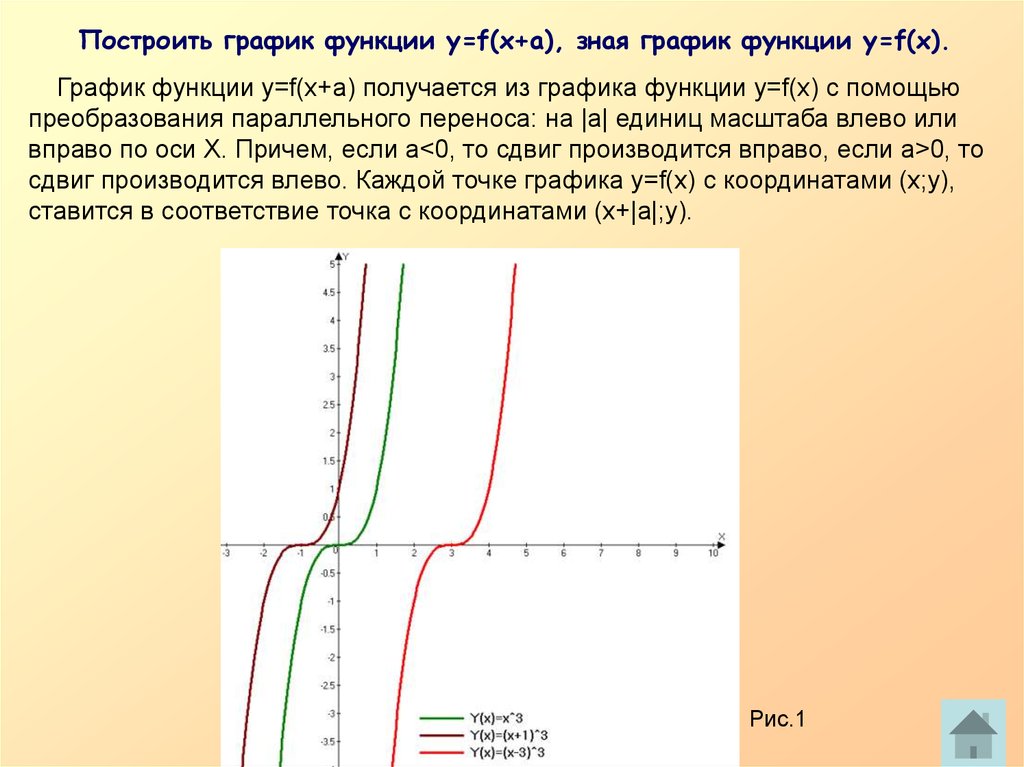
Построить график функции у=f(x+a), зная график функции у=f(x).
График функции у=f(x+a) получается из графика функции у=f(x) с помощью
преобразования параллельного переноса: на |а| единиц масштаба влево или
вправо по оси Х. Причем, если а<0, то сдвиг производится вправо, если а>0, то
сдвиг производится влево. Каждой точке графика у=f(x) с координатами (х;у),
ставится в соответствие точка с координатами (х+|а|;у).
Рис.1

5.

Построить график функции у=f(x)+b, зная график функции у=f(x).
График функции у=f(x)+b получается из графика функции у=f(x) с помощью
преобразования параллельного переноса: на |b| единиц масштаба вверх или
вниз по оси У, причем если b>0, то сдвиг производится вверх, если b<0, то сдвиг
производится вниз. Каждой точке графика функции y=f(x) с координатами (х;у)
соответствует точка с координатами (х; у+|b|).
Рис.2

6.

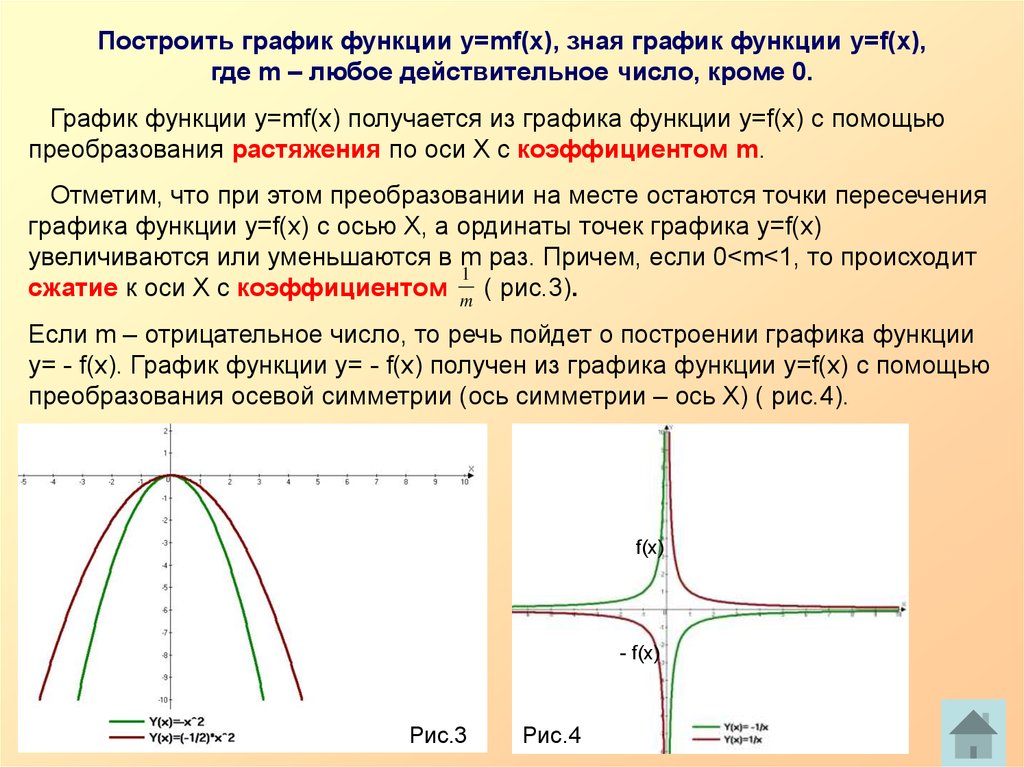
Построить график функции у=mf(x), зная график функции у=f(x),
где m – любое действительное число, кроме 0.
График функции у=mf(x) получается из графика функции у=f(x) с помощью
преобразования растяжения по оси Х с коэффициентом m.
Отметим, что при этом преобразовании на месте остаются точки пересечения
графика функции у=f(x) с осью Х, а ординаты точек графика у=f(x)
увеличиваются или уменьшаются в m раз. Причем, если 0<m<1, то происходит
1
сжатие к оси Х с коэффициентом m ( рис.3).
Если m – отрицательное число, то речь пойдет о построении графика функции
у= - f(x). График функции у= - f(x) получен из графика функции у=f(x) с помощью
преобразования осевой симметрии (ось симметрии – ось Х) ( рис.4).
f(x)
- f(x)
Рис.3
Рис.4

7.

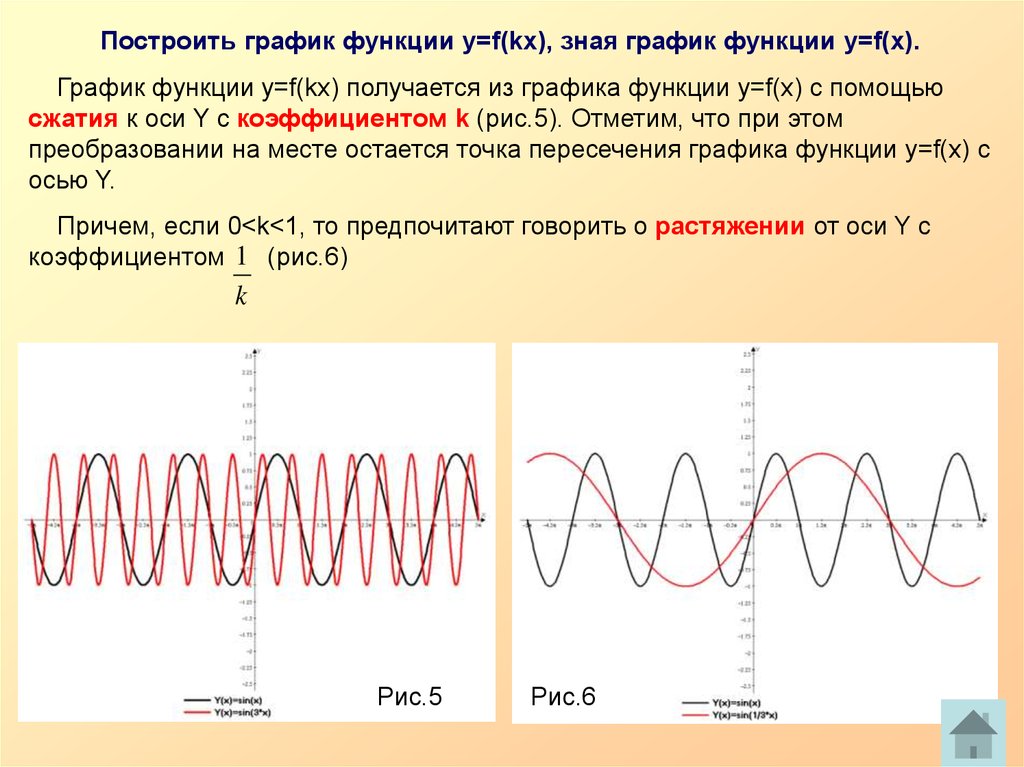
Построить график функции у=f(kx), зная график функции у=f(x).
График функции y=f(kx) получается из графика функции у=f(x) с помощью
сжатия к оси Y с коэффициентом k (рис.5). Отметим, что при этом
преобразовании на месте остается точка пересечения графика функции у=f(x) с
осью Y.
Причем, если 0<k<1, то предпочитают говорить о растяжении от оси Y с
коэффициентом 1 (рис.6)
k
Рис.5
Рис.6

8.

Построить график функции у= - mf(kx+a)+b.
f(x)
f(kx)
f(kx+a)
mf(kx+a)
- mf(kx+a)
- mf(kx+a)+b
f(x)
f(kx)
f(kx+a)
mf(kx+a)
-mf(kx+a)
-mf(kx+a)+b
Искомая функция
Рис.7

9.

Применение метода сдвигов и деформаций при построении графиков
тригонометрических функций.
Тригонометрические функции используются для описания колебательных процессов.
Этот важнейший процесс описывается формулой:
- уравнение гармонических колебаний. A, , имеют определенный физический смысл: A амплитуда колебаний ( – А, если А<0);
s A sin( t )
частота колебаний; начальная фаза колебаний.
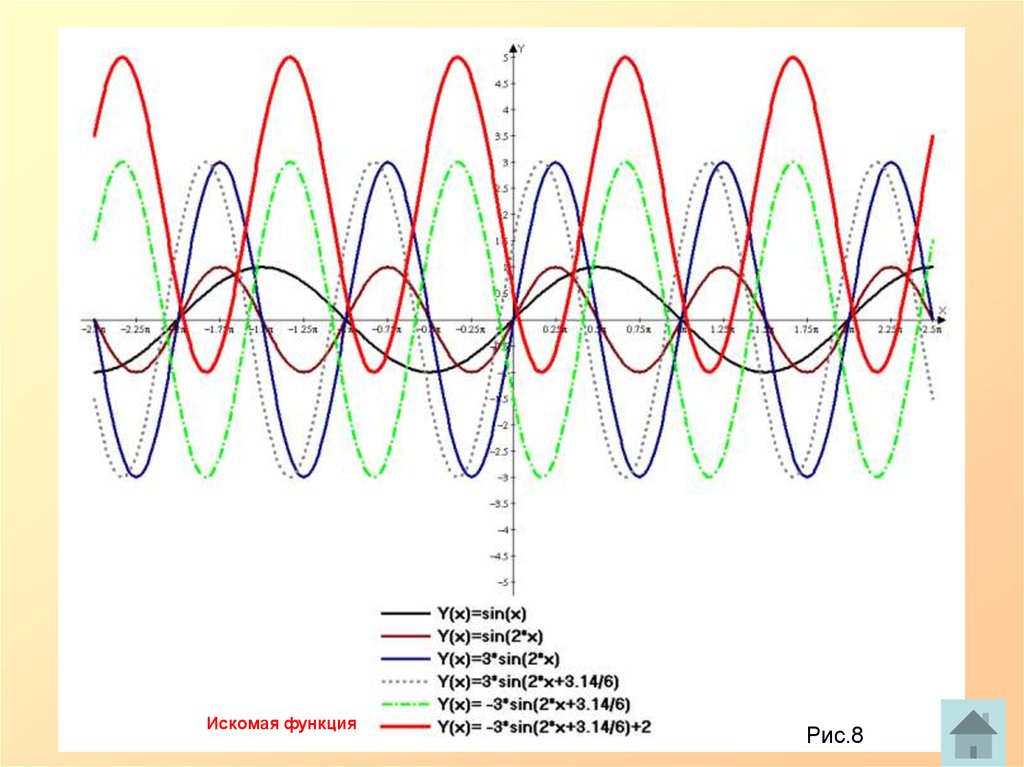
Рассмотрим уравнение вида:
у 3 sin 2( x ) 2
6
Чтобы построить график этой функции, нужно над полуволной синусоиды осуществить
следующие преобразования:
1. Сжать ее к оси Y с k=2.
2. Растянуть от оси X с k=3.
3. Сжатую и растянутую полуволну сдвинуть вдоль оси Х на
6 влево.
4. Построить полуволну синусоиды, симметрично полученной относительно оси Х.
5. Сдвинуть полученную полуволну синусоиды вверх на 2 единицы масштаба.
6. С помощью полученной полуволны получить искомый график.

10.

Искомая функция
Рис.8

11.

Модули.
Для построения всех типов графиков достаточно хорошо понимать
определение модуля и знать виды простейших графиков, изучаемых в школе.
Так, для построения графика функции у = f(|x|) на основании модуля имеем:
f ( x), если х 0,
y f (| x |)
f ( x), если х < 0.
Следовательно, график функции y=f(|x|) состоит из двух графиков:
y=f(x) – в правой полуплоскости, y=f(-x) – в левой полуплоскости.
Правило 1. Если функция y=f(|x|) – четная, то для построения ее графика
достаточно построить график функции y=f(x) для всех х 0 из области
определения и отразить полученную часть симметрично оси ординат.
Знание этого правила облегчает построение графиков функций вида y=f(|x|).

12.

Пример:
2
x
3 x 2, если x 0,
y x 2 3 | x | 2 2
x 3 x 2, если x 0.
Рис.10
Рис.9
Искомая функция
Рис.11
Рис.12

13.

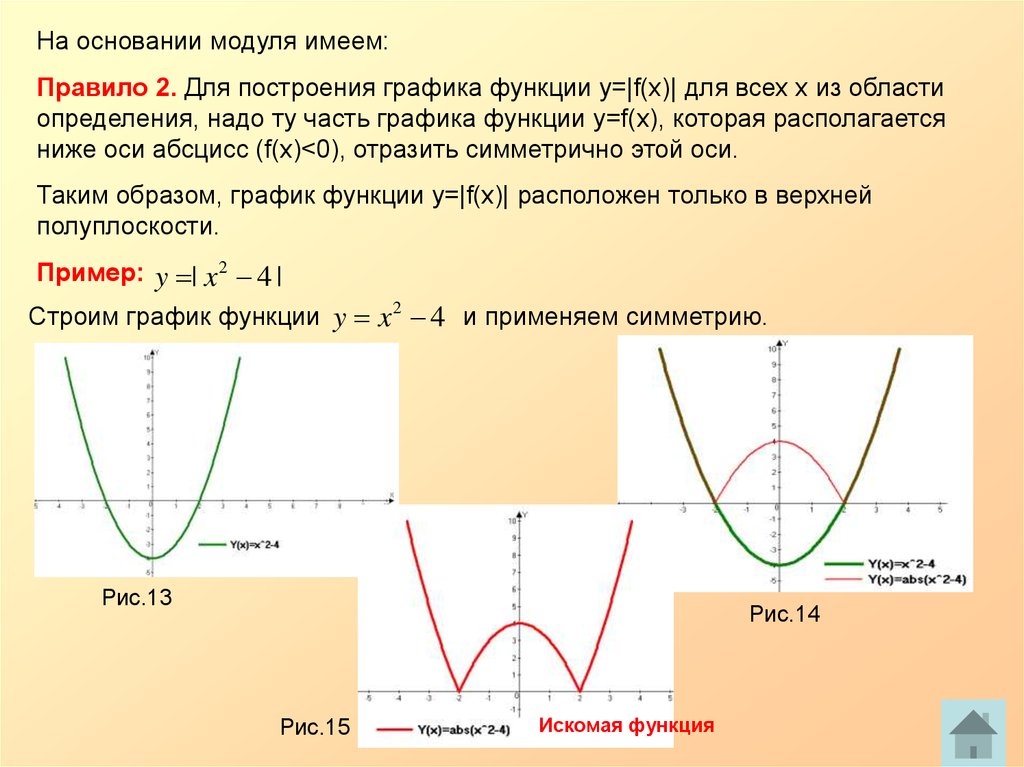
На основании модуля имеем:
Правило 2. Для построения графика функции y=|f(x)| для всех х из области
определения, надо ту часть графика функции y=f(x), которая располагается
ниже оси абсцисс (f(x)<0), отразить симметрично этой оси.
Таким образом, график функции y=|f(x)| расположен только в верхней
полуплоскости.
Пример: y | x 2 4 |
Строим график функции y x 2 4 и применяем симметрию.
Рис.13
Рис.14
Рис.15
Искомая функция

14.

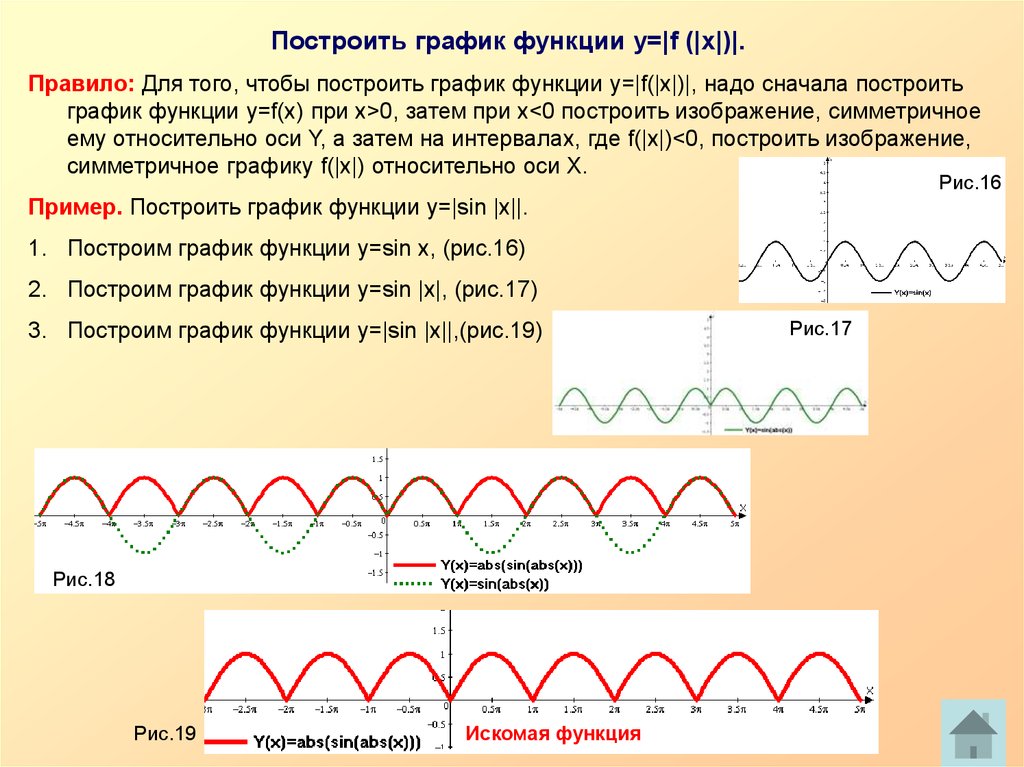
Построить график функции y=|f (|x|)|.
Правило: Для того, чтобы построить график функции y=|f(|x|)|, надо сначала построить
график функции y=f(x) при x>0, затем при x<0 построить изображение, симметричное
ему относительно оси Y, а затем на интервалах, где f(|x|)<0, построить изображение,
симметричное графику f(|x|) относительно оси Х.
Рис.16
Пример. Построить график функции y=|sin |x||.
1. Построим график функции y=sin x, (рис.16)
2. Построим график функции y=sin |x|, (рис.17)
3. Построим график функции y=|sin |x||,(рис.19)
Рис.18
Рис.19
Искомая функция
Рис.17

15.

Упражнения.
Задание: 1) Разбить функцию на подфункции. 2) Построить графики
подфункций разным цветом с легендой в программе AGRAPHER.
3) Сохранить график в своей папке под именем «График №…».
«Запомните, друзья,
Суть истины такой
Теория мертва без
практики живой»
1) y 2 x 2 1
2) y x 4
3) y sin 2 x
4) y ( x 2)3
5) y sin 3 x 1
6) y 3 cos 2 x
1
7) y | x |
2
1
8) y | | 1
x
9) y | ( x 2)( x 3) |
«В задачах тех ищи удачу
Где получить рискуешь
10) y cos( x ) 2
3
сдачу»
1
11) y | cos | x ||
2
12) y | x 2 6 | x | 8 |
«Сложность задач повышаем
Решенье найти предлагаем»

16.

Задача – исследование.
Дана функция
y x2 .
В программе AGRAPHER:
Вспомним все, что мы учили!
Ничего, ведь, не забыли?
Отображаем, двигаем, сжимаем
Графики мы точно знаем!
1. Осуществите осевую симметрию графика относительно оси Х.
2. Выполните сдвиг графика на 2 единицы вверх.
3. Выполните сдвиг графика на 1 единицу влево.
4. Произведите сжатие графика в 2 раза к оси Y.
5. Отразите ту часть графика, которая располагается ниже оси абсцисс,
симметрично этой оси.
Результат построения сохраните в своей папке под именем
«Исследование».

17.

Основные результаты.
Ребята, Вы систематизировали и обобщили правила сдвигов и деформаций,
применяемых для построения графиков сложных функций.
Вы научились строить графики функций:
y mf (kx a ) b
y f (| x |)
y | f ( x) |
y | f (| x |) |