Похожие презентации:
Кинематика материальной точки
1. КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ.
2.
1. КИНЕМАТИКА МАТЕРИАЛЬНОЙТОЧКИ.
2. СКОРОСТЬ И УСКОРЕНИЕ В
КРИВОЛИНЕЙНОМ ДВИЖЕНИИ.
3. ТАНГЕНЦИАЛЬНОЕ И
НОРМАЛЬНОЕ УСКОРЕНИЕ
3. Кинематика – изучает движение тел, не рассматривая причины, которые это движение обуславливают. Материальная точка – тело,
форма и размеры которогонесущественны в условиях данной задачи.
Механическое движение – это изменение взаимного расположения тел
или их частей в пространстве с течением времени.
Любое движение твердого тела можно представить как комбинацию
поступательного и вращательного движений.
Поступательное движение – это движение, при котором любая
прямая, жестко связанная с телом, остаётся параллельной своему
первоначальному положению.
Вращательное движение – это движение, при котором все точки тела
движутся по окружностям, центры которых лежат на одной и той же
прямой, называемой осью вращения.
4. Система отсчета. Траектория, длина пути, вектор перемещения
Движение тел происходит в пространстве и вовремени. По этому для описания движения
материальной точки надо знать, в каких местах
пространства эта точка находилась и в какие моменты
времени она проходила то или иное положение.
Тело отсчета – произвольно выбранное тело,
относительно которого определяется положение
остальных тел.
Система отсчета – совокупность системы координат и
часов, связанных с телом отсчета.
5.
•Положение произвольной точки Мхарактеризуется радиусом-вектором r ,
соединяющим начало координат О с точкой М:
r x i y j z k
Z
•Движение материальной точки полностью
определено, если декартовы координаты
материальной точки заданы в зависимости от
времени t
x x(t )
y y(t )
М
k
z z (t )
j
i
•Эти уравнения называются кинематическими
О
уравнениями движения точки. Они эквивалентны
одному векторному уравнению движения точки
r r (t )
•Линия, описываемая движущейся материальной
точкой (или телом) относительно выбранной
системы отсчета называется траекторией.
X
Рис. 1.
Y
6.
В зависимости от формы траектории движение может быть прямолинейным икриволинейным. Длиной пути точки называется сумма длин всех участков
траектории, пройденных этой точкой за рассматриваемый промежуток времени
s s (t ) .
Длина пути – скалярная функция времени
(рис.2.).
Z
Вектор перемещения r r ro
- вектор,
проведенный из начального положения
движущейся точки в положение её в данный
момент времени
А
r r ro r (t ) r (to ) x i y j z k
ro
s
r
В
r
Y
В пределе t 0 длина пути по хорде s и
длина хорды r будут всё меньше
отличатся:
ds dr dr
X
Рис. 2.
7.
СкоростьСкорость – это векторная величина, которая определяет как
быстроту движения, так и его направление в данный момент
времени.
м
Единица скорости .
с
Модуль мгновенной скорости равен первой производной пути по
времени
r
s ds
lim
lim
t 0 t
t 0 t
dt
Отсюда:
ds dt
Мгновенная скорость – векторная величина, равная первой
производной по времени от радиуса-вектора r рассматриваемой
точки:
r dr
lim
r
t 0 t
dt
8.
Вектор мгновенной скорости направлен по касательной ктраектории в сторону движения. При неравномерном движении
модуль мгновенной скорости с течением времени изменяется.
Поэтому можно ввести скалярную величину - среднюю
скорость неравномерного движения.
s
t
При прямолинейном движении точки направление вектора
скорости сохраняется неизменным.
Движение точки называется равномерным, если модуль
её скорости не изменяется с течением времени ( const ), для
него
s t
Если модуль скорости увеличивается с течением времени, то
движение называется ускоренным, если же он убывает с
течением времени, то движение называется замедленным.
9.
УскорениеУскорение – это векторная величина
характеризующая быстроту изменения скорости по
модулю и по направлению.
м
Единица ускорения - 2 .
с
Мгновенное ускорение материальной точки –
векторная величина, равная первой производной по
времени скорости рассматриваемой точки (второй
производной по времени от радиуса-вектора этой же
точки):
d d r
a lim
2 r
t 0 t
dt
dt
2
10.
В общем случае плоского криволинейного движениявектор ускорения удобно представить в виде суммы
двух проекций (рис. 3.)
n
1
2
n
n
n
a lim
lim
lim
lim
an a
t 0 t
t 0
t 0 t
t 0 t
t
a an a
2
Рис. 3.
11.
Тангенциальное ускорение a характеризует быстроту измененияскорости по модулю, его величина
d
a
dt
Нормальное (центростремительное) ускорение a n направлено по
нормали к траектории к центру её кривизны и характеризует
быстроту изменения направления вектора скорости точки.
Величина нормального ускорения связана со скоростью движения
и величиной радиуса:
n 2
d n 2
n
t
an
R
t
R
dt
R
2
a
Величина полного ускорения (рис. 4.):
a a a
2
n
2
an
a
Рис. 4.
12.
Уравнение движения (виды движения)a 0, an 0 - прямолинейное равномерное движение: a 0
a a const , an 0
- прямолинейное равнопеременное
(равноускоренное) движение. Если t 0 0,
то
0 0
a a
;
t
t t0
t
0 a t;
13.
s sisi
t
t
at 2
s 0 at dt 0t
2
0
t1
t i
t2
t
Рис. 5.
2
a 0, an const
R
- равномерное движение по окружности.
a 0, an 0 - криволинейное равнопеременное
движение.
14.
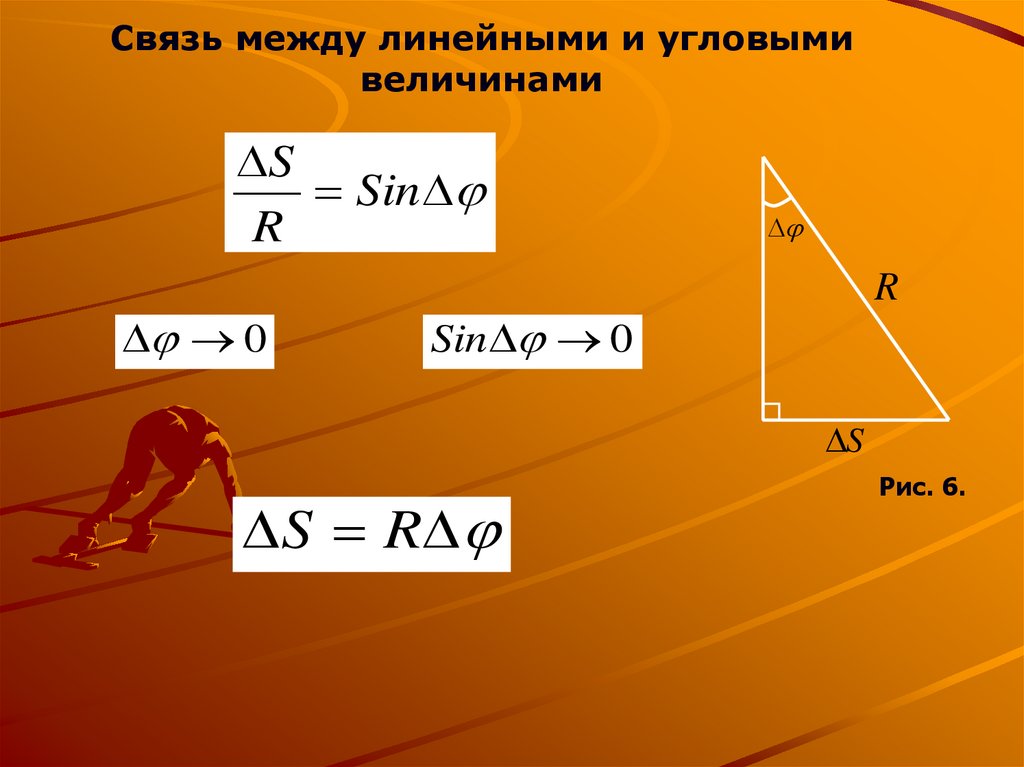
Связь между линейными и угловымивеличинами
S
Sin
R
0
R
Sin 0
S
S R
Рис. 6.
15.
S R0
S
R
lim
lim
R lim
R
t 0 t
t 0 t
t 0 t
t
R
- Угловая скорость
Единица измерения угловой скорости
рад
[ ]
с
16.
Ra lim
lim
R lim
R
t 0 t
t 0 t
t 0 t
t
a R
- Угловое ускорение
Единица измерения угловой скорости
рад
[ ] 2
с















 Физика
Физика








